集装箱船强度评估中运动和加速度相关公式的适用性分析
2022-07-19徐敏王刚王旌生
徐敏,王刚,王旌生
(中国船级社 上海规范研究所,上海 200135)
油船散货船共同规范(以下简称CSR和CSR-H)推出后之所以能够大大提高油船和散货船2种船型的结构安全,对造船业发挥了巨大的指导作用,其中一个重要原因就是,规范的制定符合了国际海事组织目标型建造标准的要求,并广泛应用了当前船舶科学发展前沿的新技术。如CSR的船舶运动和加速度公式就直接来源于国际船级社协会波浪载荷会议(以下简称AHG_WD-SL)的研究成果,CSR-H在此基础上也仅对纵摇运动和纵摇加速度作了少量局部修正,AHG_WD-SL公式对散货船和油船表现出良好的适用性,见图1。
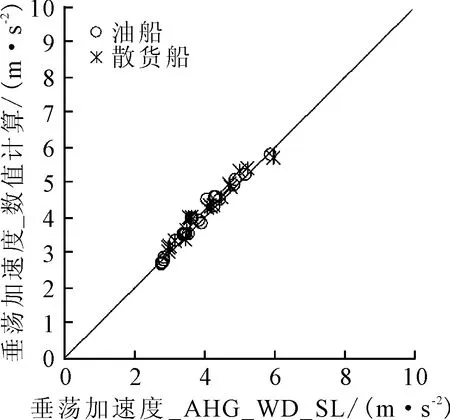
图1 重心处垂荡加速度AHG_WD-SL公式结果和数值计算结果对比
由于近年来集装箱船海损事故不断,国际海事组织已确定未来将目标型建造标准应用到集装箱船,国际船级社协会各成员也陆续开展集装箱船目标型规范的研究和制定。为此,围绕AHG_WD-SL制定的船舶重心处运动和加速度公式能否适用于集装箱船规范中的强度评估这一关键问题,通过船长范围约150~400 m的15型集装箱船实船的水动力数值计算结果和AHG_WD-SL公式计算结果对比分析,表明,由于集装箱船具有不同于油船和散货船的船型特征,AHG_WD-SL给出的船舶运动和加速度公式计算结果与水动力数值计算结果之间差别较大,大部分公式不能直接应用于集装箱船的强度评估,需要进行修正,以下将作详述。
1 AHG_WD-SL公式简介
为满足油船和散货船共同规范的制定和工程应用需求,国际船级社协会波浪载荷会议(AHG_WD-SL)经过研究,确定以船舶基本参数如船长、船宽、初稳心高等作为输入参数,给出油船和散货船的运动及加速度简化公式,其中包括船舶重心处的横摇运动、纵摇运动、纵荡加速度、横荡加速度、垂荡加速度、横摇加速度和纵摇加速度的包络值简化公式。其中,纵摇角(°)的简化公式如下。

(1)
式中:为强度评估系数;为重力加速度;为规范船长。
由于公式较多,不详细列出,具体可见参考文献[1]。
2 重心处运动加速度数值计算方法简介
2.1 坐标系及船舶运动方程
1)原点。位于对称纵剖面、船长尾端与基线的相交处;
2)轴。纵向轴,向前为正。
3)轴。横向轴,向左为正。
4)轴。垂向轴,向上为正。
船舶在波浪中的摇荡运动属于刚体6自由度运动。由于船-波浪系统的阻尼效应,经过一段足够长的时间后,运动响应将趋于稳定的周期性变化状态,即所谓的“稳态”运动。在稳定状态下,船舶位移向量()}将作为以遭遇的频率为变化频率的简谐量,见式(2)。
()=ei=()ei
(2)
式中:(=1,2,…,6)为复数振幅,依次指纵荡、横荡、垂荡、横摇、纵摇、艏摇。
根据刚体动力学原理导出船舶在波浪中的运动方程的矩阵形式如下。
纳入2016年7月至2017年6月期间,我院接受治疗的脑出血患者114例作为本研究观察对象,所有患者均确诊为脑出血,同时处于急性发病期,出血量在15~30ml,符合甘露醇治疗的标准,排除糖尿病和肝肾功能障碍的患者。结合患者接受治疗的先后顺序分为对照组和观察组,两组分别57例。对照组患者中男性32例,男性25例,年龄在45~83岁,平均为59.8岁;观察组患者中男性33例,男性24例,年龄在45~82岁,平均为59.7岁。两组患者的年龄、性别构成以及病情严重程度等资料无数据差异。
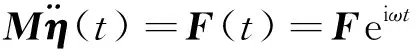
(3)
式中:为刚体的质量矩阵;()为外力列向量,可按照势流理论进行计算。
2.2 波浪环境条件及计算工况
根据集装箱船的典型装载特点,在装载手册中选取达到或接近结构吃水的满载工况和初稳心高最大的正常压载工况作为计算工况。由于国际海事组织尚未正式发布集装箱船的目标型建造标准,为了使数值计算与AHG_WD-SL公式制定保持相同的波浪环境和船舶寿命,确定集装箱船的航行波浪环境为北大西洋海况,设计使用年限为25年。强度评估时,假定在极限波浪载荷条件下,船舶航速为5 kn,采用10超越概率水平。经过水动力数值计算并进行波浪谱分析和长期预报得到船舶重心处各运动和加速度分量的极限值,即运动和加速度的长期预报值。数值计算考虑特定的横摇阻尼并基于如下假定。
1)浪向角为0°~360°,浪向间隔为15°。
2)波浪角频率为0.2~1.8 rad/s,角频率间隔为0.05 rad/s。
3)谱分析采用Rec.34北大西洋波浪散布图。
4)其他如风、流、冰、温度等环境载荷忽略不计。
3 实船计算
3.1 实船样本
选取15型样本集装箱船(C1~C15),采用中国船级社WALCS软件进行水动力数值计算,以得到样本船重心处运动和加速度的数值解。样本船基本参数见表1。

表1 样本船基本参数
3.2 实船计算结果
通过15型样本船的水动力计算,预报得到了满载和压载工况10次方超越概率组合浪向下船舶重心处运动、加速度的长期值。如,C1船满载工况下,10次方超越概率下横摇角长期极值为23°。将这些数值计算得到的长期值与按照AHG_WD-SL公式计算后的结果进行对比,见图2~8。

图2 横摇运动 AHG_WD-SL公式结果和数值计算结果对比

图3 纵摇运动 AHG_WD-SL公式结果和数值计算结果对比

图4 纵荡加速度 AHG_WD-SL公式结果和数值计算结果对比
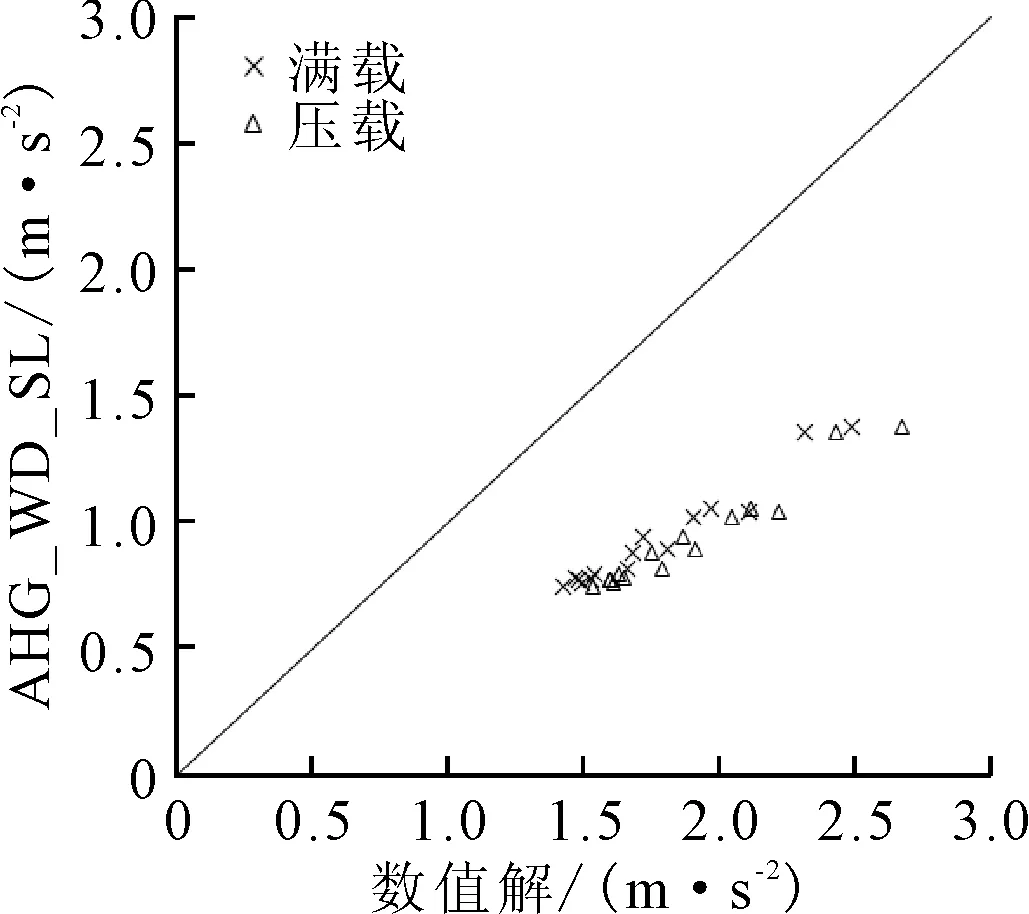
图5 横荡加速度 AHG_WD-SL公式结果和数值计算结果对比
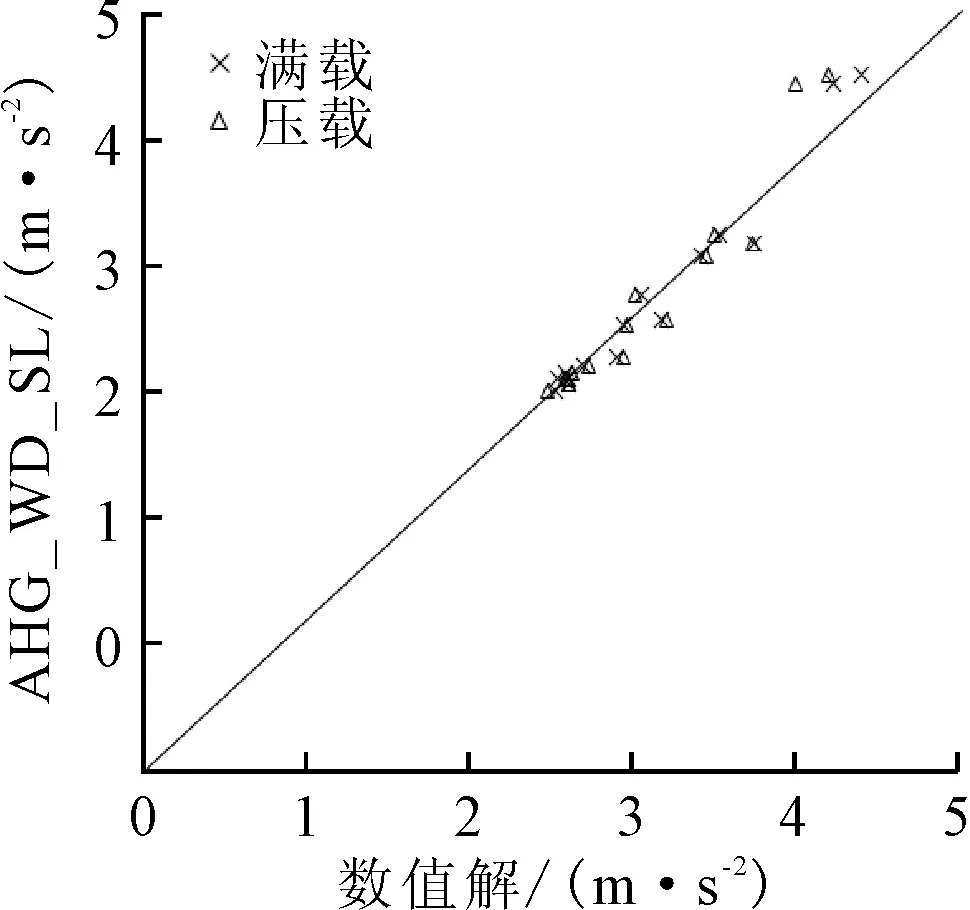
图6 垂荡加速度 AHG_WD-SL公式结果和数值计算结果对比
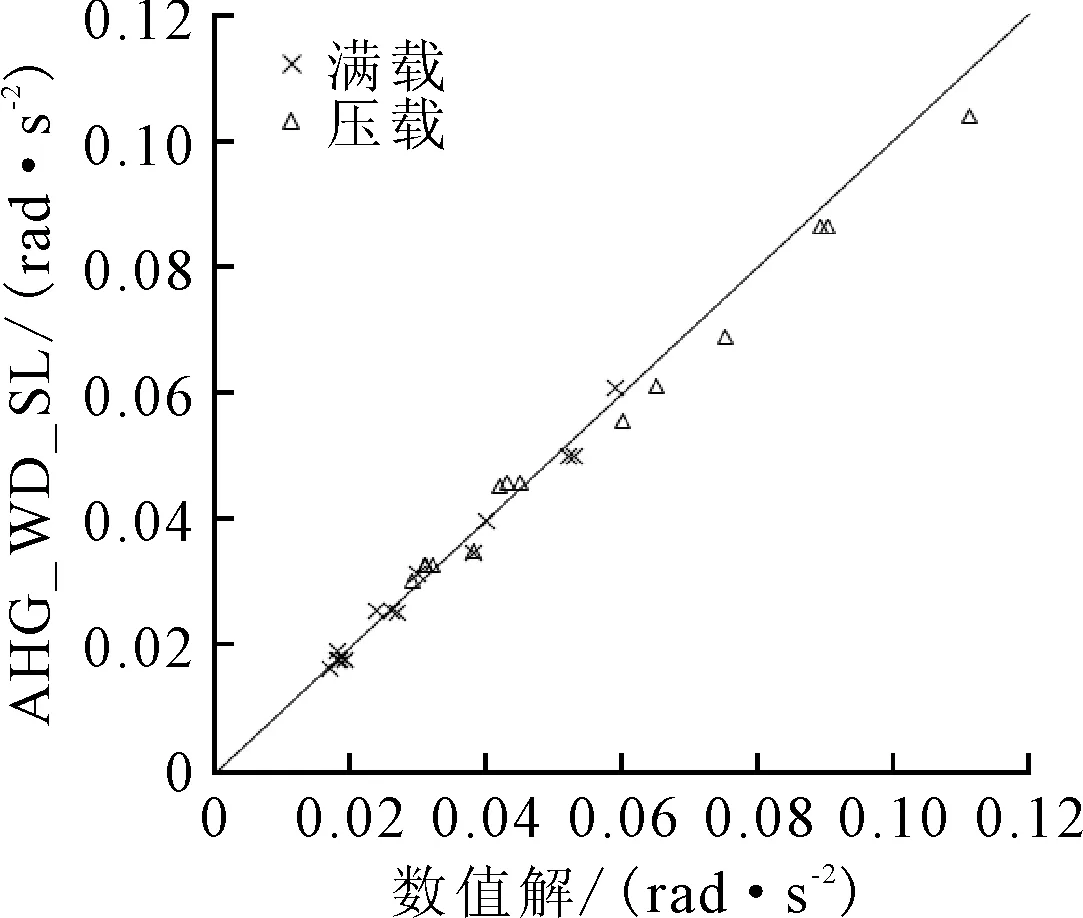
图7 横摇加速度 AHG_WD-SL公式结果和数值计算结果对比
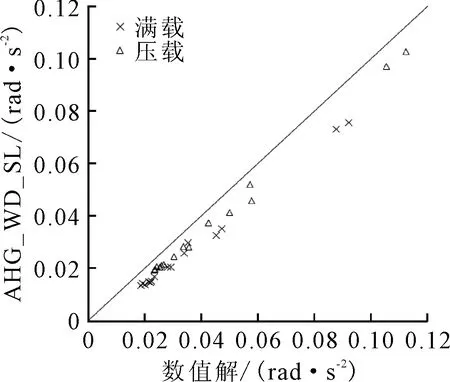
图8 纵摇加速度 AHG_WD-SL公式结果和数值计算结果对比
从图2~8可以看出,对于集装箱船重心处的运动及加速度,除横摇运动和横摇加速度外,纵摇运动、纵荡加速度、横荡加速度、垂荡加速度和纵摇加速度AHG_WD-SL公式结果和数值计算结果的符合性都较差,这些分量的AHG_WD-SL公式不能直接适用于集装箱船强度评估中的载荷计算,需要进行修正。
3.3 AHG_WD-SL公式修正
通过对这15型实船AHG_WD-SL公式结果和数值计算结果之间误差的分析,引入修正因子并回归成相对简单的经验公式来实现对AHG_WD-SL公式的修正。首先构造通用数学模型如下。
=+(,,,,,,)
(4)
式中:为纵摇运动、纵荡加速度、横荡加速度、垂荡加速度和纵摇加速度的修正因子;、、为公式待定系数;为规范船长;为船宽;为型深;为实际工况下的吃水;为船舶结构吃水;为水线面系数;为方形系数。
在进行公式回归时,发现通过单个船舶基本参数的变化,回归结果都比较差,往往无法获得理想的修正因子简化公式。且不同的船舶参数对纵摇运动、纵荡加速度、横荡加速度、垂荡加速度和纵摇加速度的修正因子的相关性也都不一样。以垂荡加速度和纵摇加速度为例。
1)、、等自变量对于因变量垂荡加速度修正因子的相关性不显著,复相关系数最大也仅有02左右,对于因变量垂荡加速度修正因子的相关性则非常显著,复相关系数超过了0.9。
2)、等自变量对于因变量纵摇加速度修正因子的相关性不显著,复相关系数最大也仅有05左右,但+或+共同作用下对于因变量纵摇加速度修正因子的相关性则非常显著,复相关系数超过了0.9。
为计算装载条件下吃水与规范船长的比值,为船宽与规范船长的比值。、、、作为自变量时,垂荡加速度修正因子的回归相关性分析结果及、、(+)、(+)作为自变量时,纵摇加速度修正因子的回归相关性分析结果见表2。
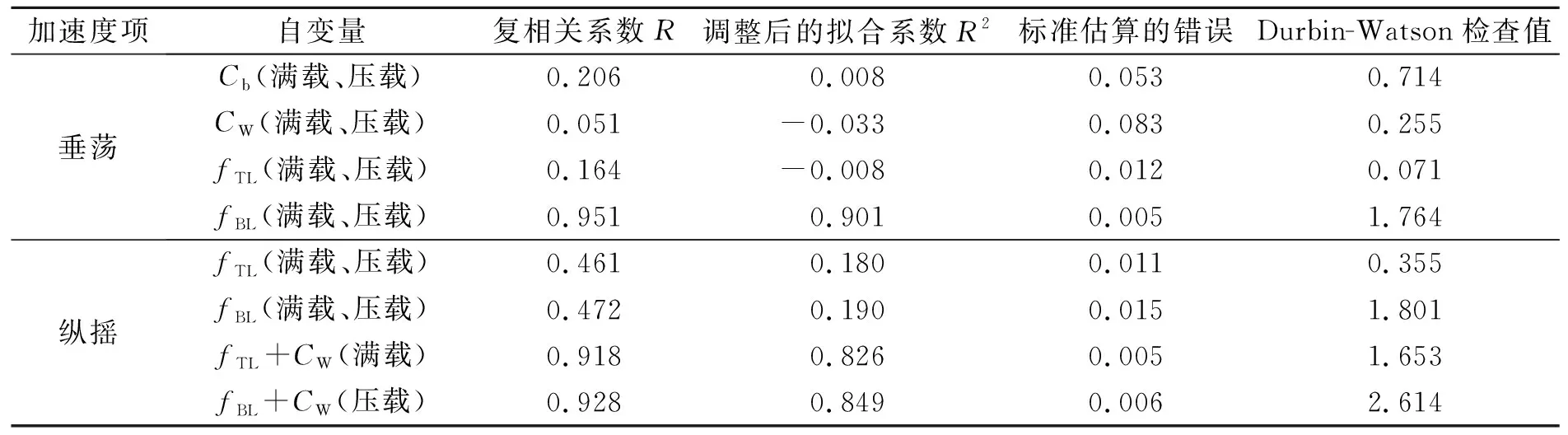
表2 加速度修正因子f4、f5回归分析结果
通过如上相关性分析和对自变量的反复调整,最终回归得出纵摇运动、纵荡加速度、横荡加速度、垂荡加速度和纵摇加速度修正因子比较合理且与数值解误差较小的简化公式。其中,垂荡加速度修正因子和纵摇加速度修正因子的简化公式如下。
=145-289
(5)

(6)
将纵摇运动、纵荡加速度、横荡加速度、垂荡加速度和纵摇加速度的数值解与引入修正因子的AHG_WD-SL公式(简称新公式)计算后的结果进行对比见图9~13。

图9 纵摇运动新公式结果和数值计算结果对比
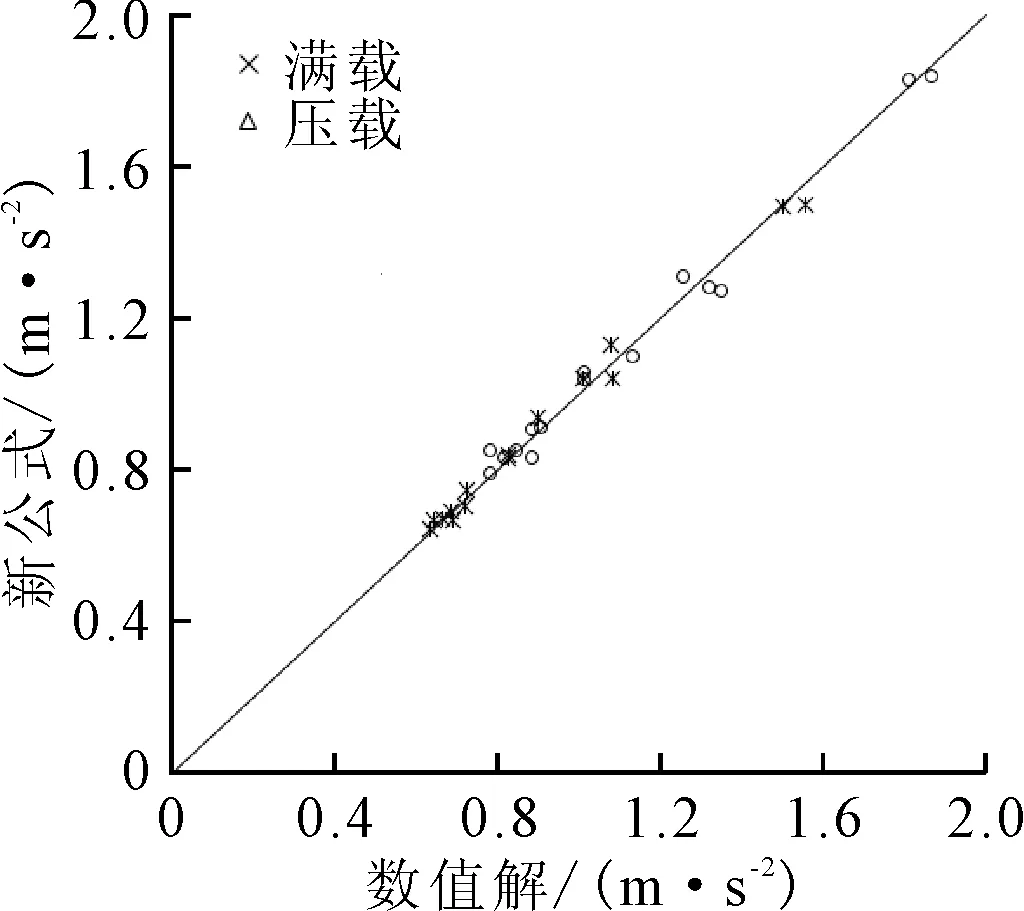
图10 纵荡加速度新公式结果和数值计算结果对比
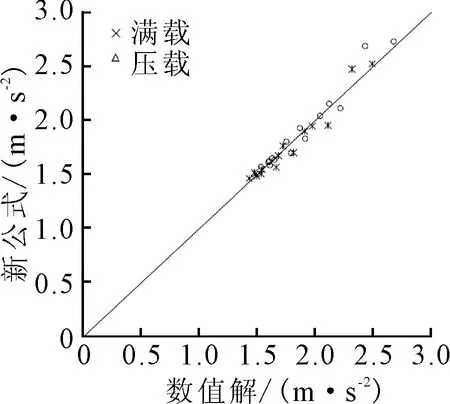
图11 横荡加速度新公式结果和数值计算结果对比
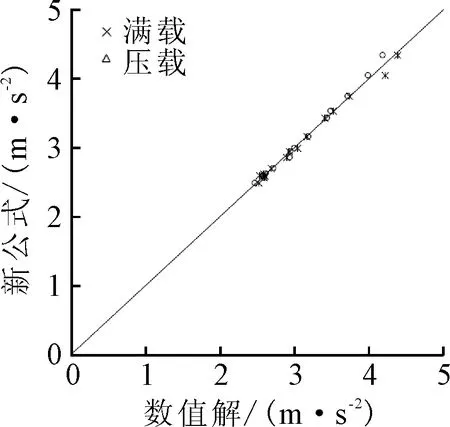
图12 垂荡加速度新公式结果和数值计算结果对比
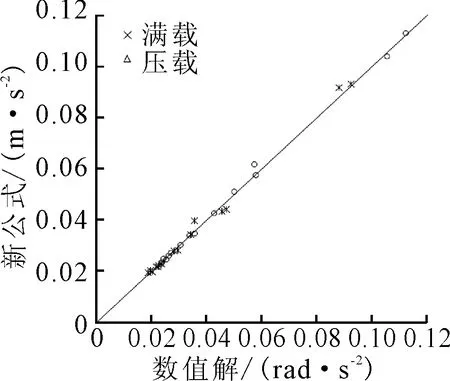
图13 纵摇加速度新公式结果和数值计算结果对比
可见新公式结果和数值计算结果的符合性都较为理想。
4 结论
1)国际船级社协会波浪载荷会议制定的用于强度评估的船舶重心处运动和加速度公式对于散货船和油船适用性良好;但对于集装箱船来说,
除横摇运动及横摇加速度公式外,纵摇运动、纵荡加速度、横荡加速度、垂荡加速度和纵摇加速度公式的适用性较差。
2)在AHG_WD-SL公式中引入以多项船舶基本参数为自变量的修正因子形成新公式,可以实现集装箱船船舶重心处纵摇运动、纵荡加速度、横荡加速度、垂荡加速度和纵摇加速度公式计算结果与数值计算结果的高度吻合,新公式适用性良好,可以直接应用到集装箱船强度评估。
