Differentiable Automatic Data Augmentation by Proximal Update for Medical Image Segmentation
2022-07-18WenxuanHeMinLiuYiTangQinghaoLiuandYaonanWang
Wenxuan He, Min Liu, Yi Tang, Qinghao Liu, and Yaonan Wang
Dear editor,
This letter presents an automatic data augmentation algorithm for medical image segmentation. To increase the scale and diversity of medical images, we propose a differentiable automatic data augmentation algorithm based on proximal update by finding an optimal augmentation policy. Specifically, on the one hand, a dedicated search space is designed for the medical image segmentation task. On the other hand, we introduce a proximal differentiable gradient descent strategy to update the data augmentation policy, which would increase the searching efficiency. Results of the experiments indicate that the proposed algorithm significantly outperforms state-of-the-art methods, and search speed is 10 times faster than state-of-the-art methods.
Deep neural networks have made great progress in medical image segmentation and contributed to the rapid development of intelligent healthcare in recent years [1]. It is conducive to the surgical planning,pathological analysis, and disease diagnosis of patients. A variety of medical segmentation models have been proposed based on obtained training data [2], [3], the performance of which depends heavily on large-scale labeled data, while medical images are extremely difficult to obtain. This is because the increasing awareness of patients’privacy protection makes it more difficult to obtain patient case data,and many professional physicians need to spend a lot of time and effort labeling medical images for deep learning-based methods [4].Moreover, multimodal data of diseases are characterized by a large span and low density due to the variety of diseases and various inspection methods. Therefore, it still has many challenges in medical image segmentation.
Data augmentation is an effective way for enlarging data size,which has been commonly employed in computer vision tasks with remarkable results [1], [2], [4]−[7]. More specifically, data augmentation is regularly utilized to address the problem of insufficient medical image data. Typical data augmentation methods in medical image segmentation include rotation, vertical flip, and random scaling [1], [4]. Since large differences exist in the samples for different types of diseases, resulting in different optimal data augmentation policies. And some experiments in [8] demonstrate that selecting an inappropriate data augmentation policy will reduce the segmentation accuracy. In other words, we need to redesign a reasonable and effective data augmentation policy for a new medical segmentation task, which requires professional experience and a variety of time to manually adjust the probability and the magnitude of the data augmentation operations. Additionally, the model [9] is also used to generate extra data, but it may not be optimal for the specific task because of the large variation in organs, tissues, and lesions and the connection of spatial contexts in medical images.Therefore, it is necessary to develop an automatic data augmentation algorithm for medical image segmentation. In this letter, we propose an automatic data augmentation algorithm to find the optimal data augmentation policy. Firstly, a dedicated search space is designed for the medical image segmentation task. Then an optimization strategy is proposed to transform the automatic data augmentation problem into a single-step optimization problem, which is resolved by a proximal differential update. The experimental results on the publicly available liver tumor dataset, the publicly available pneumothorax dataset, and our private liver tumor dataset demonstrate that the proposed algorithm achieves state-of-the-art performance with the basic network architecture. Besides, the efficiency of the search policy of the proposed algorithm is improved by at least one order of magnitude compared to existing algorithms.
Related work:Deep neural networks have made significant progress in medical image segmentation. Currently researchers generally utilize UNet [2] and its variants nnUNet [1], UNet++ [4],etc. for medical image segmentation tasks.
Data augmentation is critical to the generalization performance and robustness properties of the network with only a relatively small number of training samples available. A combination of expert handdesigned augmentation strategies is commonly used for medical image segmentation. Valanarasuet al. [10] apply the horizontal flip,vertical flip, and addNoise to the task of brain anatomy segmentation,and Ronnebergeret al. [2] apply shift, rotation, and elastic deformations to the microscopical images during preprocessing. However,these combinations of transformations are manually designed, which consumes the massive efforts of experts, and segmentation accuracy is hard to improve. Different from these methods, the first automatic data augmentation algorithm in [11] is proposed to find augmentation policies automatically based on reinforcement learning. However,this method takes 768 GPU hours by searching the probability of the augmentation policy. In [12], network weights and parameters can be optimized simultaneously with less time than in [11], but the time taken to find a reasonable policy is still hard to meet the requirements of the researchers [12]. In contrast, differentiable automatic data augmentation (DADA) [13] greatly reduces the time cost of searching policy in a differentiable way. Nevertheless, it also has the problem of the inaccurate searched policy and being not robust [13].Moreover, medical images differ from natural images, which contain spatial contextual information, a smaller dataset size, and diverse morphologies of lesions and tissues. Thus, the transformations in natural images are hard to be adapted to medical images. To this end,we develop a novel and huge search space. Moreover, an efficient and accurate search algorithm is proposed. The proposed algorithm flow is as follows: The original training set is firstly divided into a training set and a validation set. Then a data augmentation sub-policy is sampled from the search space and applied to the training set.Meanwhile, in the search stage, the network weights are updated and used for forward propagation, when the validation set loss is used to update the data augmentation policy parameters by proximal differentiable gradient descent. The above process is repeated until the loss of the validation set is converged. Finally, in the retraining stage, we selectN= 25 sub-policies with the highest probability for expanding the scale of the original training set for network retraining,as shown in Fig. 1.
Problem statement:The automatic data augmentation (DA)algorithm finds the optimal DA policy for model training. The DA policy is composed ofN= 25 sub-policiesssampled from search spaceS, which has a vector parametera(the probability of applying the sub-policies). A sub-policy contains two operations sampled from search spaceS, which are applied in sequence. Every operation has two parameters:b(the probability of applying the operation) andv(the magnitude of the operation).Ois a set of image processing operations. The original training set is divided into a training set Φtrainand a validation set Φval. The optimization objective is to find the optimal parameters ={a,b,v} by minimizing the validation lossLvalwhen training lossLtrainis converged via updating network weightw. Then the data augmentation policy optimization framework is represented as
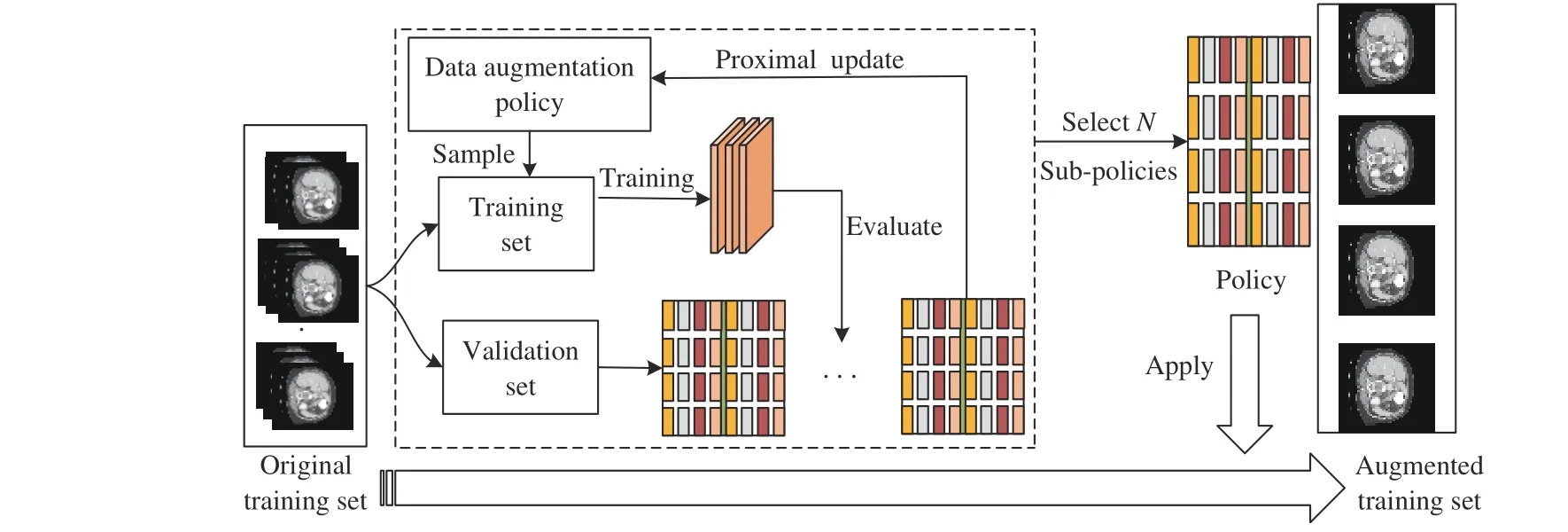
Fig. 1. The structure of the proposed algorithm.
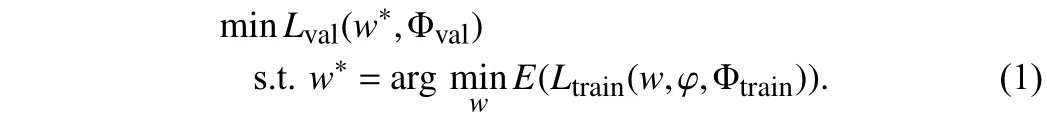
Search space:Since the automatic data augmentation algorithm needs to be employed for medical image segmentation, a dedicated search space is designed for diverse morphologies of tissues and lesions in medical images. We select 17 operations containing pixellevel and spatial-level transformations from albumentations [14],which are suitable for the variety of diseases and the uniqueness of the lesions in medical image, including contrast, randomgamma,brightness, clahe, gaussnoise, horizontalflip, verticalflip, elastictransform, opticaldistortion, gridfistortion, randomscale, rotate, shiftscalerotate, translateX/Y, shearX/Y. A data augmentation policy consisting of 136 sub-policies is sampled from the search spaceS. To increase the diversity of policies, we set the magnitude of operations in a continuous range. Therefore, we need to determine the scope of the interval. Besides the magnitude of the operation, the probabilities of applying these operations are also to be searched. The range of magnitudes and possibilities of the seventeen operations are illustrated in Table 1.
Proposed search algorithm:Based on (1), since the gradient ofφis not available directly,φis difficult to be updated via gradient descent. To this end, we use Gumbel-Softmax [13], [15] to approximate the discrete parameterφto continuous values, and then validation lossLvalis differentiable toφ. Finally, an efficient optimization method is introduced to updateφwith discrete constraints andwby proximal gradient descent.
Firstly, the sub-policy selection and operation application are sampled from Categorical and Bernoulli distributions, respectively[13]. In order to determine which sub-policy is selected, probabilityhis sampled from the Categorical distributionH.
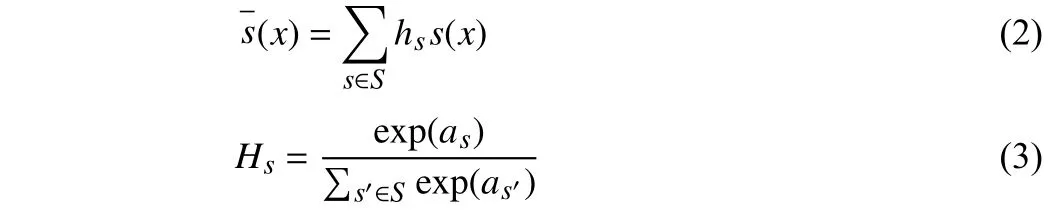
wherexdenotes image.
To estimate the gradient of the DA policy parameters {a,b}, the Gumbel-Softmax reparameterization trick is utilized to make the parameters {a,b} differentiable. Next, we describe in detail the differentiable of relaxation of sub-policy selectionaand operation applicationb. With the Gumbel-Softmax reparameterization, (2)could be represented as
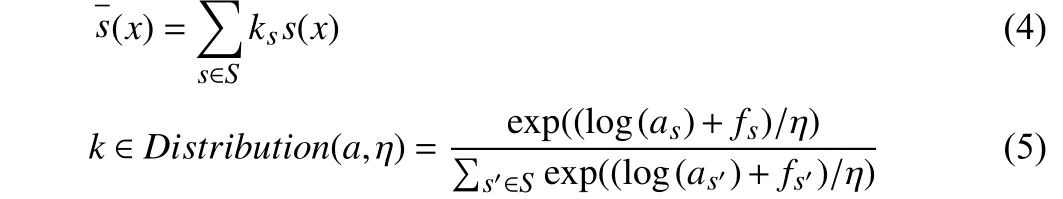
wheref=−log(−log(µ)) with µ∼Uniform(0,1), andηis thetemperature coefficient. Then, the reparameterization is applied to the Bernoulli distribution [13]
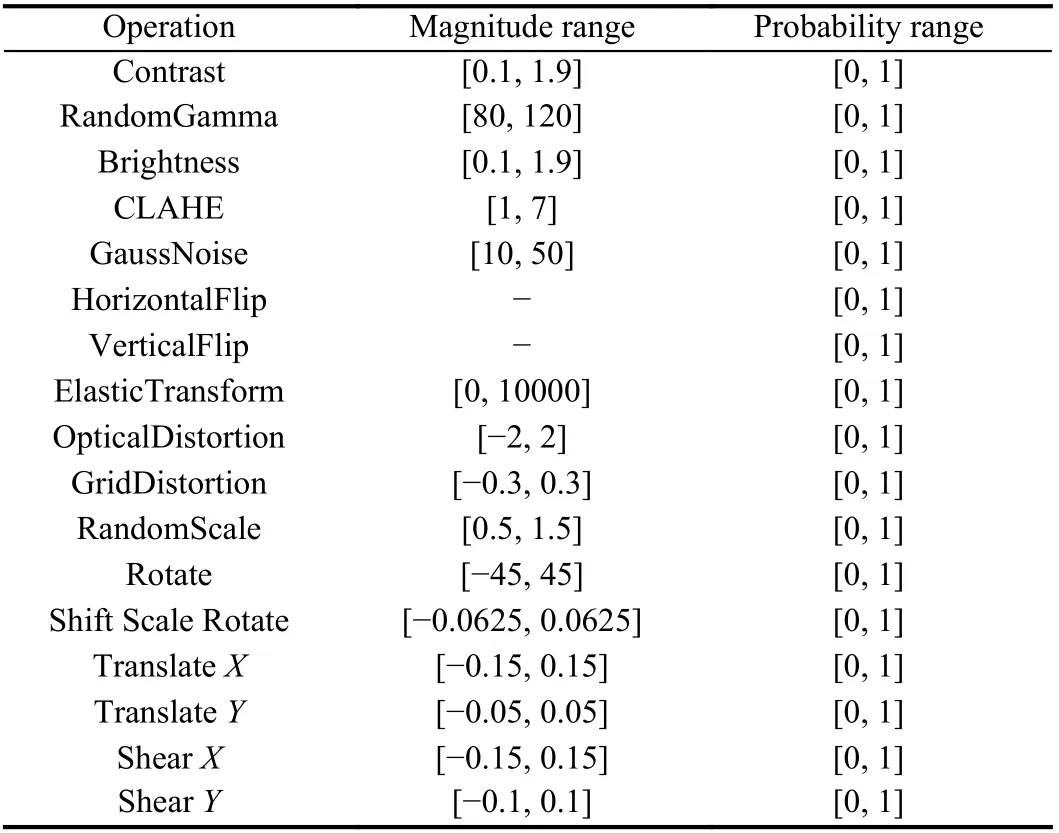
Table 1.The Designed Search Space for Medical Image Segmentation
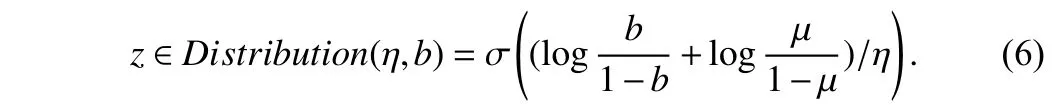
The magnitude parametervis optimized by approximating the gradient. Since the magnitude parameter is not differentiable, we apply a gradient estimator [13], [16] to optimize it for an image,
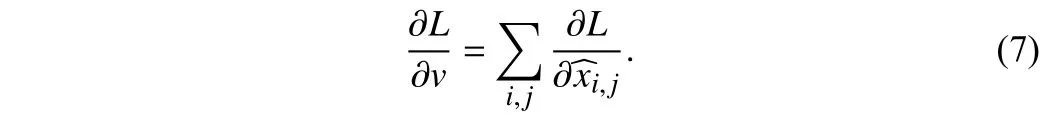
With the reparameterization trick, we keep {a,b} continuous,which is optimized by gradient descent, but constrains the selections of {a,b} to be discrete. Therefore, we generalize (4) as below:
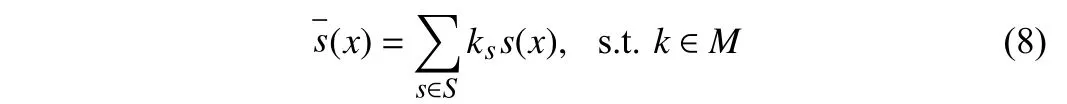
whereM={k|||k||0=1, and 0 ≤ks≤1}. Whilekis continuous to be differentiable,kis a one-hot vector when sampled. We formulate the applications of the combination of operations with the same discrete constraint. Then, the selection of operationszis sampled.
The proximal algorithm could quickly solve such convex optimization problems: A part of the objective function may be nondifferentiable, but it can be split into the sum of a differentiable convex function and a non-differentiable convex function [17]. The proximal algorithm is difficult to obtain reasonable solutions with discrete constraints. And proximal algorithm cannot be applied with the additional constraint.
To solve the optimization problem as minLval(w∗,Φval), following[17], a similar proximal algorithms is adopted. We optimizeφas a continuous variable subject to the constraintQ2. The discreteis constrained during the iteration by the constraintQ1derived fromφ.We denoteQ=Q1∩Q2, whereQ1={φ//ks//0=1and 0 ≤//zi//0≤2}andQ2={φ|0 ≤ks,zi≤1}. Then, the proximal update is given by
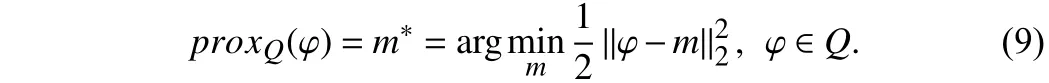
The constraintQ1is meant to imply thatm*could be expressed asjdi, wherejis the parameter to be determined anddiis a vector that contains the value 0 or 1. Letφbe ann-dimensional vector, and (9) is divided into n problems to be resolved
The procedure of the proposed algorithm is given in Algorithm 1.
Algorithm 1 The Proposed Algorithm

Dataset:We conducted experiments on three datasets including the publicly available LiTs dataset, the publicly available pneumothorax dataset, and our private liver tumor dataset.
The LiTs dataset is a publicly available liver tumor dataset containing liver and tumor labels. The dataset is provided by the 2017 Liver Tumor Segmentation Challenge organized by Medical Image Computing and Computer Assisted Intervention and IEEE International Symposium on Biomedical Imaging. The training set and the test set contain 130 CT scans and 70 CT scans, respectively.
The pneumothorax dataset is also a publicly available dataset containing only pneumothorax labels. The dataset is provided by Society for Imaging Informatics in Medicine-American College of Radiology (SIIM-ACR) pneumothorax segmentation. The training set contains 10 712 images and the test set has 1377 images.
The liver tumor dataset is an unpublished dataset containing the liver tumor label. The dataset is provided by a tertiary care hospital in Changsha, China, which contains 107 liver tumor CT scans of patients. This dataset is divided randomly into a training set and a test set in the ratio of 4:1.
Evaluation metrics:For the segmentation task, the common evaluation metrics are used [1], [4]: Dice coefficient and IoU.
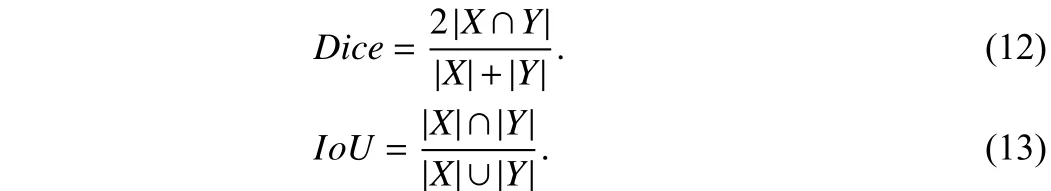
Implementation detail:As the test set labels of the LiTs dataset are unpublished, we need to submit the predictions of the test set.Since the number of submissions is limited, we compare only two well-known methods: UNet and nnUNet on the LiTs datasets. The Dice coefficient is the main evaluation metric on the LiTs and pneumothorax datasets.
Our experiments are divided into two parts: the data augmentation policy search stage and the network retraining stage. We divide the training set into two parts, half for optimizing the policy parameters and the remaining for updating the network weights in the policy search stage. Firstly, the top-25 sub-policies are obtained, when the validation loss is converged. Then the searched sub-policies are applied to the model for retraining. The model is trained using a cross-entropy loss function with a standard stochastic gradient descent (SGD) optimizer and a learning rate of 0.001. The data augmentation parameters are optimized using an Adam optimizer with a learning rate of 0.005 and a weight decay of 0. All experiments are implemented based on PyTorch and the model is trained on an NVIDIA RTX 2080Ti.
Comparisons with state-of-the-art methods:We aim to search for a group of data augmentation sub-policies suitable for multiple medical image segmentation tasks, and then the sub-policies obtained from the search stage are applied to common medical segmentation networks, such as UNet [2], UNet++ [4], DenseUNet, MANet [18],nnUNet [1], and FPN [19]. DenseNet [20] achieves better performance with fewer parameters and computational costs by linking features on channels to achieve feature reuse. Densenet161 is chosen as the encoder for UNet, which is a variant of UNet, called DenseUNet. We conducted comparison experiments on liver tumor,LiTs, and pneumothorax datasets, respectively.
Comparative results of liver tumor segmentation and pneumothorax segmentation are shown in Tables 2 and 3. The results in Tables 2 and 3 show that the searched data augmentation policy could improve segmentation accuracy when applied to networks.And the best segmentation results we achieve outperform current methods, especially nnUNet [1], which is considered to be the best segmentation framework in medical image segmentation. It is worth mentioning that our algorithm is used for the basic network architecture, and still achieves the best segmentation accuracy. This demonstrates the effectiveness of our algorithm. Moreover, as shown in Table 4, [11] takes 768 hours, and [12] takes nearly 100 hours.And * represents the results from the paper in Table 4. By contrast,our algorithm takes approximately 5 hours, which is at least one order of magnitude faster than [11] and [12]. Thus, the proposed algorithm has an advantage in speed.
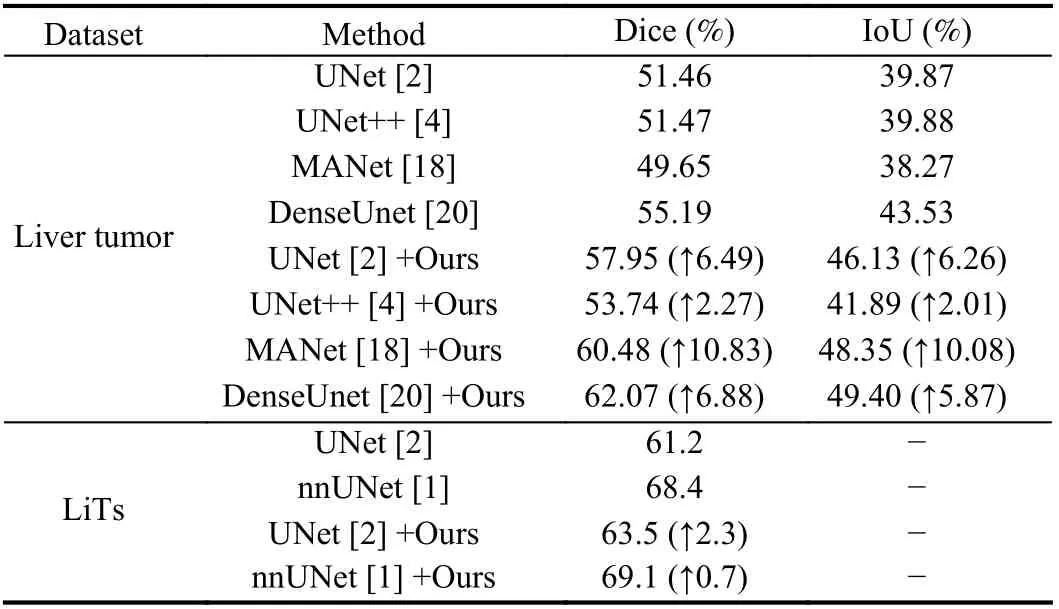
Table 2.Comparative Results of Liver Tumor Segmentation (Liver Tumor and LiTs Dataset)
Besides, we adapt the automatic data augmentation algorithm DADA [13] from the natural image domain to medical image segmentation. Then we choose the traditional data augmentation policies [1], [10] as well as DADA to compare with the proposed algorithm. In the implementation, MANet [18] is a relatively novel network for liver tumor segmentation, selected as the baseline on the liver tumor dataset, and * represents the data augmentation policy in the paper in Table 5. Additionally, UNet is selected as the baseline on the LiTs dataset, and * represents the combinations of traditional data augmentation transformations which include brightnesscontrast,randomgamma, elastictransform, griddistortion, opticaldistortion, and shiftscalerotate in Table 6 . As shown in Tables 5 and 6 , the performance of the proposed algorithm exceeds that of DADA and traditional data augmentation policies, which confirms the efficiency of the proposed algorithm. Moreover, we also plot the variation curve of the validation set loss in the search stage. As shown in Fig. 2, the proposed algorithm solves the problem that the DADA algorithm is not robust and also converges faster than DADA. These experiments demonstrate the superior robustness and convergence performance of the proposed algorithm.
Conclusions: The small scale and lack of diversity of medical image datasets, as well as the unique shapes and morphologies of different lesions, remain challenges in medical image segmentation.To solve the above problems, we firstly design a huge and novel search space that is suitable for most medical image segmentation tasks. Then, we propose a differentiable automatic data augmentation algorithm based on proximal update that searches for the optimal data augmentation policy. Finally, the comprehensive experiments demonstrate that the proposed algorithm outperforms state-of-the-art methods. And we could achieve the best segmentation accuracy by applying the searched data augmentation policy to basic network architecture. Additionally, the search speed of the proposed algorithm exceeds the best current automatic data augmentation algorithms in medical image segmentation.
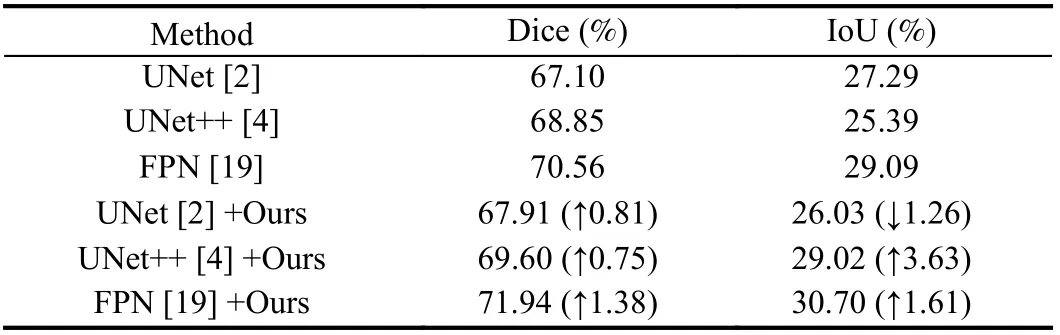
Table 3.Comparison of Pneumothorax Segmentation Results on Pneumothorax Dataset

Table 4.Comparison of GPU Hours
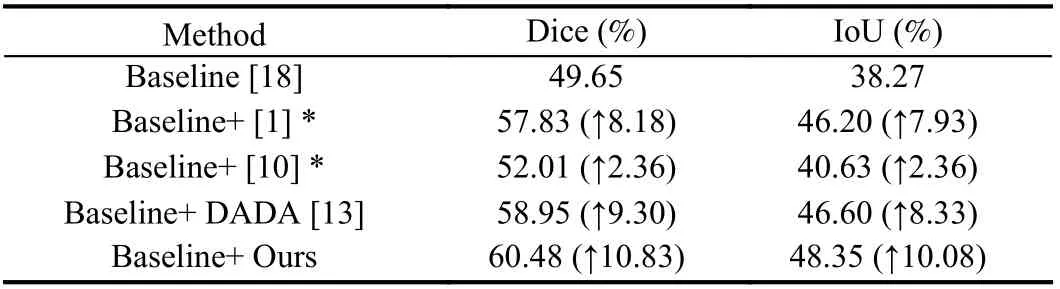
Table 5.Comparison Results of Traditional and Automatic Data Augmentation Algorithms on Liver Tumor Dataset
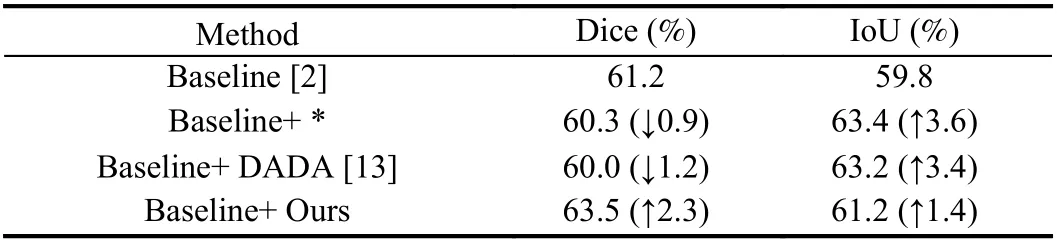
Table 6.Comparison Results of Traditional and Automatic Data Augmentation Algorithms on LiTs Dataset
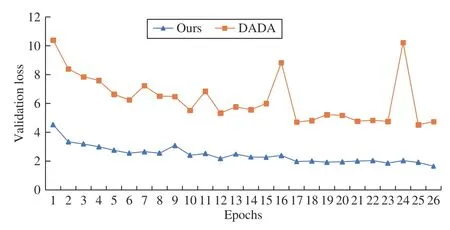
Fig. 2. Comparison results of validation set loss between ours (blue) and DADA (orange) in the search stage. Notably, the validation set loss of our method has been steadily decreasing, yet the loss curve of DADA oscillates during the search stage.
Acknowledgments:This work was supported by the National Natural Science Foundation of China (62073126), the Hunan Provincial Natural Science Foundation of China (2020JJ2008), the Key Research and Development Program of Hunan Province(2022WK2011), the Science and Technology Program of Changsha(897202102345).
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- An Overview and Experimental Study of Learning-Based Optimization Algorithms for the Vehicle Routing Problem
- Towards Long Lifetime Battery: AI-Based Manufacturing and Management
- Disagreement and Antagonism in Signed Networks: A Survey
- Finite-Time Distributed Identification for Nonlinear Interconnected Systems
- SwinFusion: Cross-domain Long-range Learning for General Image Fusion via Swin Transformer
- Real-Time Iterative Compensation Framework for Precision Mechatronic Motion Control Systems
