Disagreement and Antagonism in Signed Networks: A Survey
2022-07-18YuxinWuDeyuanMengandZhengGuangWu
Yuxin Wu, Deyuan Meng,,, and Zheng-Guang Wu
Abstract—Signed networks refer to a class of network systems including not only cooperative but also antagonistic interactions among nodes. Due to the existence of antagonistic interactions in signed networks, the agreement of nodes may not be established,instead of which disagreement behaviors generally emerge. This paper reviews several different disagreement behaviors in signed networks under the single-integrator linear dynamics, where two classes of topologies, namely, the static topology and the dynamic topology, are considered. For the static signed networks with the adjacency weights as (time-varying) scalars, we investigate the convergence behaviors and the fluctuation behaviors with respect to fixed topologies and switching topologies, respectively, and give some brief introductions on the disagreement behaviors of general time-varying signed networks. Correspondingly, several classes of behavior analysis approaches are also provided. For the dynamic signed networks with the adjacency weights as transfer functions or linear time-invariant systems, we show the specific descriptions and characteristics of them such that the disagreement behaviors can be obtained by resorting to the derived static signed graphs.Furthermore, we give their applications to the behavior analysis of static signed networks in the presence of high-order dynamics or communication delays.
I. INTRODUCTION
BEHAVIOR analysis for network systems has become one of the most fundamental and popular topics in many fields[1]–[4], which can be applied to solve, e.g., the formation control problem [5]–[8], the sensor fusion problem [9]–[12],the synchronization problem of coupled oscillators [13]–[15],and the opinion forming problem [16]–[19]. All the nodes in network systems are generally required to accomplish specific dynamic behaviors under distributed control protocols through the local information exchange among them. One of the most basic dynamic behaviors in networks systems is the consensus behavior [20]–[24], the study of which can formally be dated back to the 1970s [25]. The consensus actually shows a compromised agreement of nodes, for which the final states of all nodes are dependent on both their initial states and their interactions. Since the development of the consensus needs the collaborations among nodes, network systems admitting only cooperative interactions have been widely studied. To describe the information flow among all nodes in cooperative networks, the unsigned digraphs with only positive edges are generally adopted, due to which the cooperative networks are also called unsigned networks. Except for the consensus behavior, other significant dynamic behaviors have further been exploited for unsigned networks under various control protocols or topology conditions, such as the scaled consensus[26]–[28], the cluster [29]–[32], the synchronization [33]–[38],and the containment tracking [39]–[42].
A fact worth mentioning is that there may exist not only cooperative interactions but also antagonistic interactions among nodes in several real network systems. For example, in social networks, each individual may have either a friendly/allied or a hostile/competitive relation with other individuals[43]–[45]. To characterize such interaction relations of nodes in network systems, the signed digraph is leveraged with the positive/negative edge describing the cooperation/antagonism or like/dislike between two nodes, respectively [46]. Because of this fact, the network systems that simultaneously include the cooperative and antagonistic interactions are named signed networks. Since the antagonisms render it difficult to reach a unified agreement upon all nodes, the disagreement generally emerges in signed networks. As a consequence, the bipartite consensus rather than the consensus, which reflects a class of polarization phenomena, is of particular interest in the study of signed networks [47]–[49]. The bipartite consensus behavior can be commonly seen in many real world scenarios,such as duopolistic markets, two-party political systems, and two competitive sport teams. To realize the bipartite consensus, the structural balance property generally plays a basic role. It ensures the existence of a bipartition of nodes, where the nodes inside every group are all cooperative, but the nodes between the two groups are antagonistic [50], [51]. Given the structural balance property, signed networks can be transformed to their related unsigned networks under a linear gauge transformation.
Motivated by the natural phenomena and practical engineering problems, different dynamic models have been established for the study of signed networks. The most popular one is the first-order Laplacian-type model, which characterizes a single-integrator linear system subject to the Laplacian information flow. Under the first-order Laplacian-type model,many meaningful disagreement behaviors have been disclosed for signed networks with respect to different topology conditions, such as the bipartite consensus [47], [52], [53], the modulus consensus [54]–[57], the (quasi-)interval bipartite consensus [58]–[61], the bipartite containment tracking [62],[63], and the bipartite containment fluctuation [64]. Based on the behavior analysis results for the first-order Laplacian-type model, the high-order Laplacian-type model has further been investigated. Unlike the first-order signed networks, the dynamic behaviors of the high-order signed networks are influenced not only by the topology conditions but also by the internal characteristics of each node. This makes the behavior analysis of them much more complex [48], [49], [65], [66].Further, some other interesting dynamic behaviors have been exploited for signed networks in the presence of several specific linear models, such as the edge stability under the edge-based model [67], [68], the (bipartite) sign-consensus under the predictable model [69]–[72], and the consensus under the relative-state-flipping model [73], [74]. To capture more complicated dynamic characteristics and interaction relations of signed networks and to discover more possible disagreement behaviors, of particular interest are more than the simple linear models, which contain the nonlinear model[75], [76], the random network model [77]–[79], the fractional-order model [80]–[83], the bounded confidence model[84]–[86], the finite/fixed-time consensus model [87]–[91],and the dynamic communication model [92], [93]. It is a notable fact that the behavior analysis problem is only treated as the most essential problem for exploring signed networks,in addition to which other issues, such as the controllability problem [94]–[98] and the structural balance problem[99]–[103], are also important.
Instead of giving an extensive survey of all existing behavior analysis results and their corresponding analysis approaches of signed networks, we provide a more specific overview of those in the presence of single-integrator linear dynamics under the Laplacian flow, where both the static and dynamic topologies are involved. We firstly review the disagreement behaviors of signed networks with respect to the fixed topologies, for which three different behavior analysis approaches are given to show the similar convergence behaviors from different perspectives. It is clearly disclosed that different connectivity and structural balance properties may lead to diverse disagreement behaviors, including the bipartite consensus, the interval bipartite consensus, and the bipartite containment tracking. Secondly, the time-varying signed networks are taken into account. Via resorting to a state transition matrix-based approach, we establish the connections between signed and unsigned networks such that a complete behavior analysis framework is presented for any signed network in the presence of switching topologies, which reveals a class of leader-contained fluctuation behaviors. We further give a brief introduction on the disagreement behaviors for general time-varying signed networks. Last, we focus on the disagreement behaviors of dynamic signed networks with all communication channels composed of linear time-invariant systems. By using a frequency domain analysis approach, we investigate the disagreement behaviors for undirected dynamic signed networks and then introduce their applications to static signed networks under high-order dynamics or communication time delays.
The organization of the remainder part of this paper is given as follows. We present some preliminaries of signed digraphs and the structural balance theory in Section II. Sections III and IV show the disagreement behaviors for static signed networks with respect to fixed topologies and time-varying topologies, respectively, together with their corresponding behavior analysis approaches. In Section V, the disagreement behaviors of dynamic signed networks are discussed. We make conclusions in Section VI.
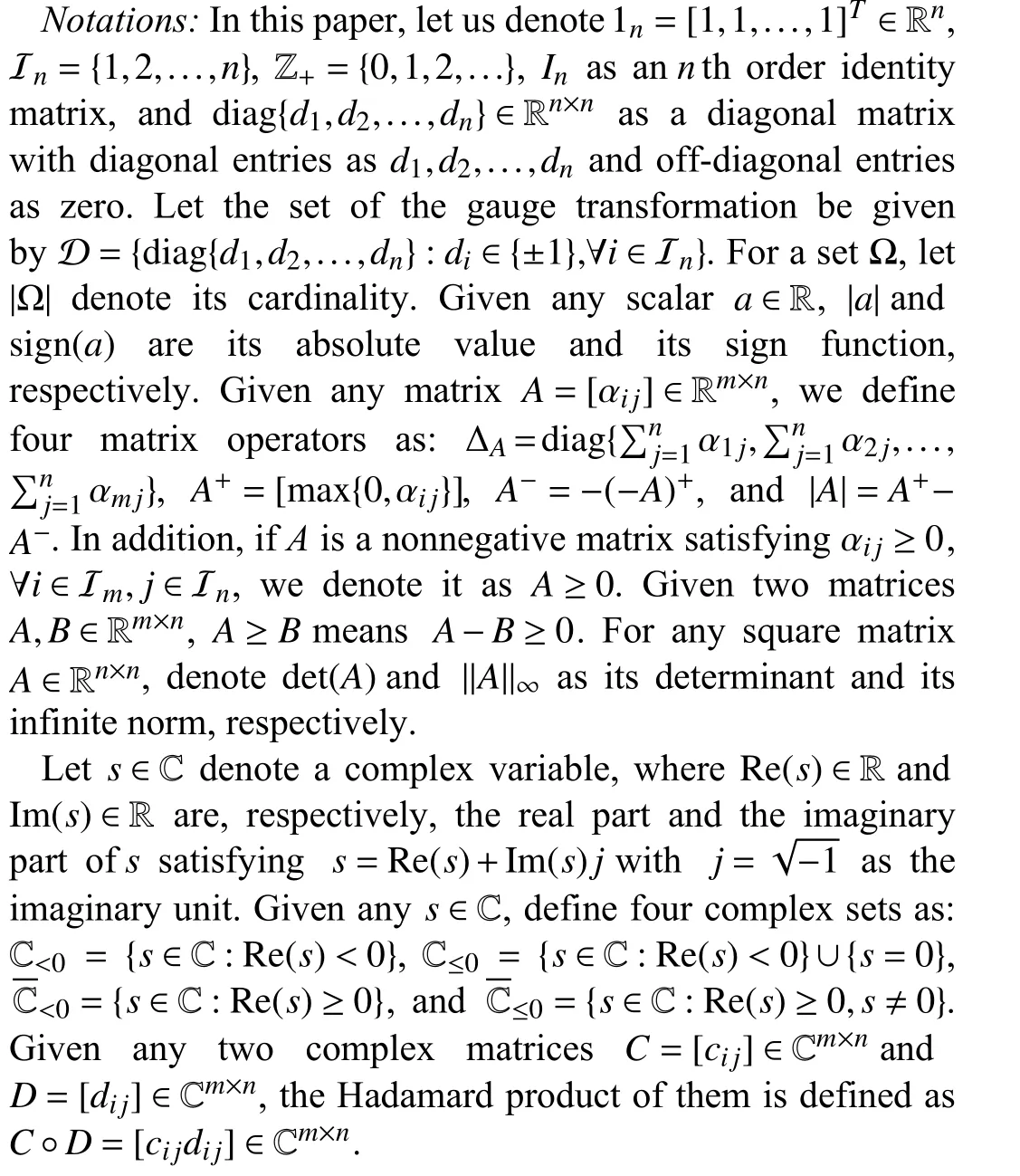
II. PRELIMINARIES
In this section, we introduce the preliminaries of the fixed and time-varying signed digraphs, which help to describe the interactions among nodes in signed networks, and present the structural balance theory. In subsequent sections, the notions for signed digraphs and those for signed networks are adopted without distinction if no confusions occur.
A. Fixed Signed Digraph
A fixed signed digraph, short for directed graph, is r epresentedbyatripleG={V,E,A},withV={v1,v2,...,vn},E ⊆V×V={(vj,vi):vi,vj∈V}, andA=[aij]∈Rn×nasthe node set, the edge set, and the weighted adjacency matrix,respectively.ai j≠0 ⇔(vj,vi)∈E; and otherwise,aij=0. We suppose that there exist no self-loops in G, i.e., (vi,vi)∉E oraii=0 , ∀i∈Inholds. If (vj,vi)∈E , thenvjis said to be a neighbor ofvi, based on which the set and the label set of all neighbors ofviare denoted as Nvi={vj:(vj,vi)∈E} and Ni={j:(vj,vi)∈E}, respectively. Ifai jaji≥0, ∀i,j∈In, then Gis said to be digon sign-symmetric; and it is digon signunsymmetric, otherwise. Given any ε>0 , theε-skeleton ofG is denoted by G[Aε], which is a deduced signed digraph ofG withthe adjacencymatrixAεsatisfying=aijif|aij|≥ε holds;andotherwise,=0.The Laplacian matrixLof Gis defined as
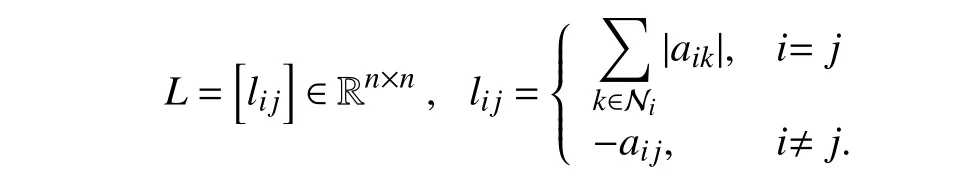
We alternatively denote a signed digraph G with the adjacency matrix A by G(A). An unsigned digraph possessing the same node set and edge set as the signed digraph G is represented by G (|A|)={V,E,|A|} with | A|≥0.
A(directed)pathfromvjtoviinGisreferredto a finite sequencewithm≥1edges {(vkl−1,vkl)∈E:1 ≤l≤m}, wherevk0=vj,vk1,...,vkm=viare distinct nodes. If there exists a dir ected path fromvjtovi,thenvjissaidto bean origin node ofvi.We denotethesetof allorigin nodesofviasMvi.If any two of the distinctnodes arethe originnodesofeachother,then G is strongly connected. For the particular undirected case thatai j=aji, ∀i,j∈In, the strong connectivity property collapses into the (weak) connectivity property. G is said to be quasi-strongly connected (or have a spanning tree) if G owns at least one nodevjbeing an origin node of all other nodes,wherevjis called a root node. We denote the root node and non-root node sets of G as Vrand Vnr, respectively.
AsigneddigraphGs={Vs,Es,As}issaidto be asubgraph of Gif it follows thatVs⊆VandEs⊆E.For anysubgraph Gs, if Esand Asare those deleting all edges in E and all columns and rows in A subject to the nodes in V Vs, then it issaidtobeasubgraphofGoverVs.Wecanclearly determinethatgiven anyVs⊆V,thesubgraphGsofGover Vsis unique. Thanks to this fact, we can directly extend the notion of neighbors to subgraphs, i.e., for any subgraph Gsof G over Vs, its neighbor set NGssatisfies
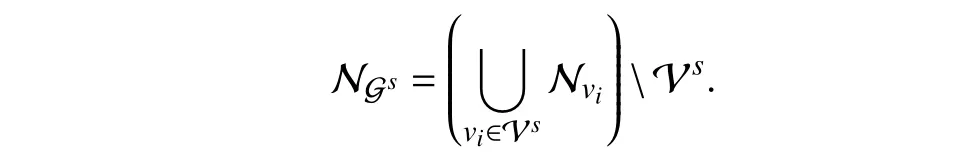
According to [62, Definition 1], a nodeviis called a leader of a signed digraph G if G has a strongly connected subgraph Gsover Vssatisfyingvi∈Vsand NGs=∅; and otherwise,viis called a follower of G. We denote the sets of the leaders and followers as L and F , respectively. Obviously,L∪F =V and L∩F =∅ hold, where all “stubborn nodes” are included as special components in L and isolated from other nodes in G[39], [104].
B. Time-Varying Signed Digraph
A time-varying signed digraph is generally in the presence of a time-varying triple G(t)={V,E(t),A(t)}, in which the three parts are in accord with those of the fixed signed digraph but E(t) and A(t) are time-varying. As a result, the neighbor label set ofvi, denoted by Ni(t)={j:(vj,vi)∈E(t)}, is also time-varying. Let={(vj,vi):|ai j(s)|ds=∞,i,j∈In}wheret0≥0 is the initial time. G(t) is said to be essentially(quasi-)strongly connected if={V,} is (quasi-)strongly connected. If theε-skeleton of the derived unsigned digraph G[|A(s)|ds], ∀t≥t0is (quasi-)strongly connected for some positive constantsT>0 and ε>0 , then G(t) is said to be uniformly (quasi-)strongly connected. It is obvious that the uniform (quasi-)strong connectivity guarantees the essential(quasi-)strong connectivity, but not vice versa. The Laplacian matrixL(t) of G (t) can be similarly given as
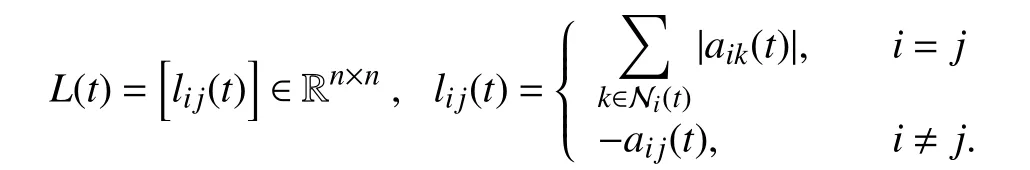
G(t)is said to be cut-balanced if there exists some constantK≥1 such that for anyt≥t0and any node partition satisfying V1∪V2=V and V1∩V2=∅, it holds
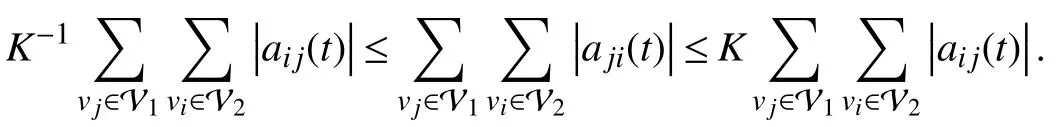
As a particular case of time-varying signed digraphs, a class of switching signed digraphs has received considerable attention. A switching signed digraph can obviously be described by a time-varying triple G(t)={V,E(t),A(t)},where G(t) switches amongMfinite signed digraphs.Specifically, it holds G(t)∈={Gσp=(V,Eσp,Aσp):p∈IM}, ∀t≥t0, where an infinite sequence {tk:k∈Z+} is admitted with the dwell timetk+1−tk≥τ for some constant τ>0 such that G(t)=Gk, ∀t∈[tk,tk+1) for a sequence{Gk=(V,Ek,Ak):k∈Z+} belonging to. The union of a collection of signed digraphs {Gk1,Gk2,...,Gk j} belonging tois described byGkp, with the node set and edge set as V andEkp, respectively. G(t) is jointly (quasi-)strongly connected if there exists some sequence {kj:j∈Z+} withk0=0 and 0 Assumption1:For anyp∈IMandany, it issatisfied that {t:G(t)=Gσp}∩[]≠∅forsomeconstantT>0. Based on Lemma 1, we can validate that under Assumption 1,ifG(t)isjointly quasi-stronglyconnected,thenthereexists somesequence {kj:j∈Z+}suchthat the unionGp=Gσp, ∀j∈Z+is quasi-strongly connected, andhence,all theroot nodesofGσpare the same as those oftheunionGp,∀j∈Z+.Consequently,wedefinetheunionroot nodesandunionnon-root nodesof G(t)astherootnodesand non-rootnodes ofGσpunderAssumption1,respectively.Inaddition,we define the union leaders andunion followers of G(t)as the leaders andfollowers ofGσp,respectively.Weleverageandtodescribethesetsoftheunionroot nodes and union non-root nodes, and L∪and F∪to represent the sets of the union leaders and union followers, respectively.We will disclose in Section IV that the union leaders (or the union root nodes) dominate the dynamic evolutions of signed networks subject to switching topologies. The structural balance property is generally referred to the sign pattern of signed digraphs, which guarantees the existence of two antagonistic node sets with internal cooperations.When the structural balance property holds, the equivalence between signed digraphs and unsigned digraphs can be built through the gauge transformation. The definition of the structural balance property is formally given as follows (see also [46], [47], [50]). Definition 1:A signed digraph G is said to be structurally balanced (s.b.) if its node set V can be decomposed as two node subsets {V1,V2:V1∪V2=V,V1∩V2=∅} fulfillingaij≥0 , ∀vi,vj∈Vpfor anyp∈{1,2} andai j≤0 ,∀vi∈Vp,vj∈Vqfor anyp,q∈{1,2} (p≠q); and otherwise, G is said to be structurally unbalanced (s.ub.). Based on Definition 1, it is easy to validate that there exists some gauge transformationD∈D renderingDAD=|A|. As a consequence, a structurally balanced signed digraph G(A) is always equivalent to its deduced unsigned digraph G (|A|), for which the alternative gauge transformationD∈D is generally non-unique. Clearly, the structural balance property given in Definition 1 is a global sign pattern of signed digraphs and it may be easily broken even under a “small flaw.” For example,given an s.b. signed digraph with an edge (vj,vi), if we make a slight change to the edge (vi,vj) such thatai jaji<0, then it becomes an s.ub. signed digraph. However, there may exist no unified ways to solve the problems subject to s.ub. signed digraphs. Thus, the definition of the global structural balance property seems too “restrictive.” To avoid this drawback, the structural balance property is generalized to concentrate on the local nodes rather than the global signed digraph itself (see also [105]). Definition 2:For a signed digraph G,viis called a structurally balancednodeif thesubgraph Gsof Goveris s.b.with=Mvi∪{vi}; andviis calleda structurallyunbalancednode, otherwise. The structural balance property in Definition 2 is developed from the viewpoint of the local nodes. Based on this definition, it is clear that all nodes of signed digraphs can be decomposed into two disjoint subsets depending on the structural balance properties of them. Then, we denote the sets of the structurally balanced and unbalanced nodes as B and U,respectively, and it fulfills B∪U=V and B∩U=∅. Actually, there exists an equivalent relationship between the structural balance property of a signed digraph and that of its nodes, which is revealed in the lemma below. Lemma 2([105,Lemma 1]):A signed digraph G is s.b.(respectively, s.ub.) if and only if B=V (respectively,B ⊂V) holds. In Lemma 2, it indicates that the global structural balance property of a signed digraph can be maintained under the consideration of the local structural balance property of nodes such that the global property of structural balance can still be determined even only given the local property of it. If G no longer has the global structural balance property, we may still benefit from the local structural balance property of nodes to explore signed digraphs, particularly when some of the nodes are of interest. Therefore, the local structural balance property may be more effective for the study of signed digraphs. Given a time-varying signed digraph, the structural balance property of the union of all alternative signed digraphs rather than that at every time instant plays a crucial role. We present the following definition of the simultaneous structural balance focusing on overall structural balance properties along the time axis for time-varying signed digraphs (see also [61], [64]). Definition 3:A signed digraph G(t) is simultaneously structurally balanced (s.s.b.) if the node set V can be decomposed as two fixed node subsets{V1,V2:V1∪V2=V,V1∩V2=∅} fulfillingai j(t)≥0, ∀vi,vj∈Vp,t≥t0for anyp∈{1,2} andai j(t)≤0, ∀vi∈Vp,vj∈Vq,t≥t0for anyp,q∈{1,2}(p≠q); and otherwise, G is said to be simultaneously structurally unbalanced (s.s.ub.). For an s.s.b. time-varying signed digraph G (t), there always exists some constant gauge transformationD∈D to guaranteeDA(t)D=|A(t)|, with which the equivalent relation between an s.s.b. signed digraph G(A(t)) and a time-varying unsigned digraph G(|A(t)|) can be developed. The simultaneous structural balance in Definition 3 is a global property of G(t),which has limitations for the study of time-varying signed digraphs. By following Definition 2, for any switching signed digraph, we can similarly provide the definition of the simultaneous structural balance for the local nodes (see also [106]). Definition 4:For a switching signed digraph G (t),viis said to be a simultaneously structurally balanced node if the subgraph Gs(t) of G(t) overis s.s.b., where{vi} withas the set of all the origin nodes ofviinGσp; and otherwise,viis said to be a simultaneously structurally unbalanced node. Denote the sets of simultaneously structurally balanced and unbalanced nodes as B∩and U∩, respectively. It follows B∩∪U∩=V and B∩∩U∩=∅. Analogously, a relation can be built for the simultaneous structural balance of a switching signed digraph and that of its nodes, i.e., G(t) is s.s.b(respectively, s.s.ub.) if and only if B∩=V (respectively,B∩⊂V ). Further, for any time instantt≥t0, G (t) has structurally balanced and unbalanced nodes, the sets of which are,respectively, denoted by B(t) and U(t). Some relations existamong the four node sets B∩, U∩, B(t), and U(t). To be specific, it holds that 1) B∩⊆B(t), ∀t≥t0; 2) U∩⊇U(t),∀t≥t0; 3) B∩∩U(t)=∅ , ∀t≥t0, but U∩∩B(t)≠∅ may be fulfilledforsome time instantt≥t0; 4)∩t≥t0B(t)=B∩⇔∪t≥t0U(t)=U∩. TABLE 1 THE COMPARISONS AMONG THREE BEHAVIOR ANALYSIS APPROACHES FOR THE SIGNED NETWORK (2) In this section, we focus on the disagreement behaviors for signed networks with respect to fixed topologies. Three classes of behavior analysis approaches are, respectively,introduced to reveal the specific characteristics of signed networks under different connectivity and structural balance properties. We consider a signed network withnnodes, which is related to a fixed signed digraph G. The dynamics of theith node under the Laplacian protocol can be given as wherexi(t)∈Risthestateoftheithnodeandaij, ∀i,j∈Inis theadjacencyweightofG.Letx(t)=[x1(t),x2(t),...,xn(t)]T,and then the dynamics of the signed network (1) can be shown in a compact form of whereLis the Laplacian matrix of G. Since the signed network (2) admits the Laplacian flow among all nodes, we call (2) the Laplacian-type model. The Laplacian-type model is the most classic model for the study of signed networks, and it exhibits various significant disagreement behaviors subject to different connectivity and structural balance properties [47],[60], [62]. In this section, the disagreement behaviors of the signed network (2) are investigated under different topology conditions, where three different behavior analysis viewpoints are discussed (see Table I for the comparisons among them).To proceed, the definitions of some common dynamic behaviors are proposed as follows. Definition 5:The signed network (2) achieves 1) modulus consensus if for anyx(0)∈Rn, l imt→∞|xi(t)|=c,∀i∈Inforsomescalarc≥0(inparticular,thebipartite consensusisrealizedifc>0 foralmostall(a.a.)x(0)∈Rnand the stability is realized ifc=0 for anyx(0)∈Rn); 2) interval bipartite consensus if for a.a.x(0)∈Rn,limt→∞=c,∀vi∈Vrfor somescalarc>0,and limt→∞≤c,∀vj∈Vnr, where thenumberofnodeswith state moduli converging tocis called the impact index of root nodes; 3) bipartite containment tracking if for anyx(0)∈Rn, From Definition 5, it is clear to see that bipartite consensus andstabilityaretwo specialcasesof modulusconsensus.For intervalbipartiteconsensus,whenlimt→∞=c,∀vj∈Vnrholds, it collapses into bipartite consensus. Further, bipartite containment tracking includes all behaviors given in Definition 5 as special cases. The signed network (2) is a linear time-invariant system,and hence, the eigenvalue distribution ofLof its associated signed digraph G plays a decisive role in its dynamic evolution. By noting that the adjacency matrix A is no longer a nonnegative matrix, it is generally not easy to directly exploit the properties of the signed digraph G. As a consequence,the derived signed undirected graph with the adjacency matrix Au=(A+AT)/2is adopted as an intermediate tool. In order to render G(Au) to maintain the similar properties of G, the digon sign-symmetry assumption is usually required [47],[60], [62]. In this subsection, if there are no special indications, we suppose that the digon sign-symmetry property is always ensured for G. With the digon sign-symmetry property, we give an equivalent structural balance result of G and G(Au). Lemma 3:Given a digon sign-symmetric signed digraph G,it is s.b. (respectively, s.ub.) if and only if G(Au) is s.b.(respectively, s.ub.). Proof:This lemma can be directly developed based on [47,Lemma 2 and Corollary 3]. ■ With Lemma 3, the eigenvalue distribution ofLfor strongly connected signed digraphs can be determined (see [47,Lemma 2 and Corollary 3]), thanks to which the convergence behaviors of the signed network (2) under the strong connectivity property can be presented in the theorem below. Theorem 1:Let G be strongly connected. The signed network(2)establishesbipar[tit econs]ensus(respectively,stability) withlimt→∞x(t)=D1n(respectively,limt→∞x(t)=0),whereD∈Dandv∈RnsatisfyDAD=|A|,vT(DLD)=0, andvT1n=1, ifandonlyifGiss.b. (respectively, s.ub.). Proof:If G is s.b., the bipartite consensus result can be concluded from the consensus result in [21] via a gauge transformation. The structural unbalance property of G leads to the positive stability ofL(see [47, Corollary 3]) such that the stability of the system (2) can be directly derived (see[108]). The necessity is a direct result of the sufficiency by noticing thatthestructural balance and unbalance properties are mutuallyexclusive.■ It shows in Theorem 1 that given the structural (un)balance property, the dynamic behaviors of the signed network (2) are confirmable under the strong connectivity property. Moreover,the structural balance leads to the disagreement of all nodes such that they converge to two different scalars, whereas the structural unbalance results in a trivial agreement of all nodes such that the impacts of their initial states disappear. However, only given the quasi-strong connectivity, the structural balance and unbalance properties of G may not be effective anymore for distinguishing the dynamic behaviors of signed networks. For a quasi-strongly connected signed digraph G,denote the subgraph of G over Vras Gr={Vr,Er,Ar} and the subgraph of G over Vnras Gnr={Vnr,Enr,Anr}, respectively.Since the root nodes can send information to the non-root nodes, but not vice versa, the Laplacian matrix of G has a special form as Lemma 4([60,Lemma 3]):If the signed digraph G is quasistrongly connected, the eigenvalues ofLnr+∆|Arnr|all possess positive realparts . From Lemma 4, it is obvious thatLnr+∆|Arnr|is positive stable in spite of the structural (un)balance property of G such that the eigenvalue distribution ofLheavily relies on that ofLr. By noting the fact that Gris always strongly connected,we can benefit from Theorem 1 to verify the eigenvalue distribution ofL, which depends on the structural (un)balance of Gr. Lemma 5:If G is quasi-strongly connected, then 1)Lhas exactly one zero eigenvalue and other eigenvalues ofLall have positive real parts if and only if Gris s.b.; 2) the eigenvalues ofLall have positive real parts if and only if Gris s.ub. Proof:Thislemma canbe derivedfrom[60, Theorem 2]together with[47, Lemma2and Corollary 3].■ Based on the eigenvalue distribution ofLrevealed in Lemma 5, the signed network (2) is always convergent regardless of the structural (un)balance of G. But different structural balance properties may lead to different dynamic behaviors, which will be disclosed in the theorem below. Theorem 2([60,Theorem 5]):Let G be quasi-strongly connected. The signed network (2) realizes interval bipartite consensus such that wherexr(0) is the initial state of root nodes, andDr∈D andvr∈RmsatisfyDrArDr=|Ar|,vr(DrLrDr)=0 , and1m=1,if and only if Gris s.b. The signed network (2) achieves stability with l imt→∞x(t)=0 if and only if Gris s.ub. Remark 1:The structural (un)balance property of Grinstead of that of G determines the dynamic behaviors of the signed network (2) with respect to a quasi-strongly connected signed digraph. It is shown in Theorem 2 that the root nodes dominate the dynamic evolution of signed networks, and all nodes finally converge within the bounded zone spanned by the converged states and the symmetric states of the root nodes in spite of the structural (un)balance property. For an s.b. G, it can be directly deduced via a gauge transformation that the signed network (2) realizes bipartite consensus, and it is evidently a particular case of interval bipartite consensus.However, only given the structural balance of Gr, the more complicated disagreement behavior emerges such that all nodes may converge to several different clusters. In comparison to the convergence results in Theorem 1, it is shown that the status inequality of nodes may lead to more disagreement behaviors. This is different from the consistent consensus results for strongly connected and quasi-strongly connected unsigned networks [21]. As a consequence, the existence of antagonistic interactions is one of the crucial inducements for the disharmony of network systems. To advance further, the general signed network without any particular connectivity property is considered. For such signed networks, all nodes can be decomposed into two groups, that is, the leader group and the follower group. By the definitions of the leaders and the followers in Section II-A, we can verify that the leaders can not receive information from nodes outside their own leader group, and the followers can gain information from at least one leader, i.e., the requirement in[62, Condition 1] always holds for the followers. Without loss of generality, assume thatthereexistkleadergroupswithminodes intheith leader group Liand∑mi=m.Wedenote thesubgraphof GoverLiasGLi={VLi,ELi,ALi},∀i∈Ikand the subgraphof GoverF asGF={VF,EF,AF},respectively. Then the Laplacian matrix of G is in the form of whereLLiandLFare the Laplacian matrices of GLi,∀i∈Ikand GF, respectively,AFL=[AFL1,AFL2,...,AFLk]=[]∈R(n−m)×mwith=a(i+m)j, ∀i∈In−m,j∈Im. Since GLi,∀i∈Ikis an isolated strongly connected subgraph of G, the dynamic behaviors of leaders can be derived according to Theorem 1, namely, each leader group establishes bipartite consensus or stability depending on its structural balance or unbalance property. Without loss of generality, we suppose that the firstpleader groups are s.b. To gain the dynamic behaviors of followers, the key problem is to investigate the eigenvaluedistributionofLF+∆|AFL|. Construct a signed digraphwith theadjacencymatrixas such that its corresponding Laplacian matrix is given by In [62, Claim 1], it validates thatis always quasi-strongly connected. By following Lemma 4, we have a similar result for theeigenvaluedistribution ofLF+∆|AFL|, i.e.,the eigenvalues ofLF+∆|AFL|all havepositivereal parts.Then,thedynamic behaviorsof the signednetwork (2) withoutany connectivity property can be obtained. Theorem 3([62,Theorem 8]):For any signed network with dynamics provided by (2), the bipartite containment tracking is achieved in spite of the structural (un)balance property of G.Moreover, each leader group realizes either bipartite consensus or stability, and the followers fulfill wherexl(t) andxf(t) are the states of leaders and followers,respectively,xLi(0) is the initial state of theith leader group,andDLi∈D andvLisatisfyDLiALiDLi=,vLi(DLiLLiDLi)=0, and1mi=1, ∀i∈Ip. Remark 2:In Theorem 3, it validates that the leader groups,especially the s.b. leader groups, dominate the dynamic behaviors of all nodes and the followers converge to the convex hull formed by the converged states of leaders and their symmetric states. In particular, if all the leader groups are s.ub., then the stability is realized. It is noteworthy that the leaders concerned in Theorem 3 refer to a class of dynamic leaders, which can dynamically evolve under the influences of other leaders, and they include the generally considered“stationary leaders” (or “stubborn nodes”) as a special case[104], [109], [110]. In addition, the convergence results in Theorem 3 include those in Theorems 1 and 2 with respect to the cases that G (t) has only one unique leader group, and more general and complex disagreement behaviors are revealed for signed networks. Thanks to Theorems 1−3, a complete framework for the behavior analysis of the first-order time-invariant Laplaciantype model has been developed, which is applicable for the signed network (2) with respect to all potential fixed topologies. This analysis framework is established by taking advantage of the properties of associated signed digraphs. As a counterpart of the continuous-time model (2), the discretetime model under the Laplacian flow has also been studied[60]. The dynamic behaviors for signed networks under the discrete-time model can generally be investigated through the similar ways as those for continuous-time cases. Therefore,some detailed discussions for disagreement behaviors under the discrete-time Laplacian-type model are omitted here. As mentioned in Section III-A, the digon sign-symmetry assumption is a common requirement for the signed network(2) when employing the graph-based behavior analysis approach. A question naturally arises: whether the digon signsymmetry property is necessary for the behavior analysis of the signed network (2). The answer is negative. Thanks to theM-matrix-based analysis approach, we can thus remove the digon sign-symmetry assumption [107]. We provide a formal definition of theM-matrix as follows (see also [111]). Definition 6:Given a square matrixA∈Rn×n, it is anMmatrix ifA∈ZnandAis positive stable with In [111, Theorem 2.5.3], it proposes an equivalent statement thatA∈Znis anM-matrix if and only ifAis nonsingular andA−1is nonnegative. This is a useful property for the following behavior analysis of the signed network (2). Since the stability of the Laplacian matrixLplays a central part in identifying the behaviors of the signed network (2), the main focus of this subsection is on the stability analysis ofLbased on the properties of theM-matrix (we refer the reader to[112] for more details of the matrix stability). Let G be strongly connected, and then the Laplacian matrixLof G can be decomposed as In [107, Lemma 4.1], it discloses thatLA++∆|A−|is anMmatrix if and only if A−≠0.As a result,LA++∆|A−|is nonsingular and (LA++∆|A−|)−1≥0 (see [111]). Let us denoteS=−(LA++∆|A−|)−1A−. By − A−≥0 and Sis obviously a stochastic matrix. Then, we can rewriteLas which is the product of anM-matrix and a diagonally dominant nonnegative matrix. Thanks to the Gershgorin circle theorem [112], the eigenvalues ofLandIn+Seither are zero or have positive real parts owing to the diagonal dominance of them. By also noting det(LA++∆|A−|)>0, we can determine the equivalence between the stability ofLand that ofIn+S.Then, the following results for the stability ofLandIn+Scan be presented. Lemma 6:For a strongly connected signed digraph G with A−≠0, the following statements hold: 1)L(orIn+S) is semi-positive stable if and only if G is s.b.; 2)L(orIn+S) is positive stable if and only if G is s.ub. Proof:The results of this lemma are direct consequences of[107, Theorems 4.1 and 4.2]. ■ With Lemma 6, the conclusions in Theorem 1 can further be drawn by taking advantage of the gauge transformation or the stability result of linear time-invariant systems. From the above analysis processes, the digon sign-symmetry assumption is never required, which pushes a little further for the behavior analysis results under the graph-based analysis approach. It is noteworthy that only the eigenvalue analysis for the Laplacian matrix of strongly connected signed digraphs makes use of the digon sign-symmetry property in Section III-A. Consequently, the results in Theorems 2 and 3 are also available without the requirement of the digon signsymmetry property by resorting to Lemma 6. The disagreement behaviors in Theorems 2 and 3 can also be developed by utilizing theM-matrix-based approach. Next,a brief outline is presented for the proof of Theorem 2 based on theM-matrix-based approach, which may motivate a new perspective for studying signed networks. For a quasi-strongly connected signed digraph, the stability ofLdepends on the stabilityofLrandLnr+∆|Arnr|( see (3)).The stabilityofLrcan be determinedby Lemma 6 becauseof thestrongconnectivity of Gr. Then, we can rewriteLnr+∆|Arnr|as From[107,Lemma 5.1],LA+nr+∆|A−nr|+∆|Arnr|is anM-matrix,underwhicha substochasticmatrixcanbe constructedas such that Combining the positive stability ofI+Snrand the nonsingularity oftheM-matrixLA+nr+∆|A−nr|+∆|Arnr|,the positive stability ofLnr+∆|Arnr|isa direct consequence thanksto the diagonal dominance ofLnr+∆|Arnr|. Consequently, the interval bipartiteconsensus resultcanthus be validated.For more detailed proof processes, the reader can refer to [107]. The previous subsections study the disagreement behaviors of the signed network (2) with respect to different connectivity conditions separately. In this subsection, a unified framework is given for the behavior analysis of signed networks in spite of any connectivity property. Section II indicates that we can divide the nodes of a signed digraphG into different disjoint subsets depending on their characteristics, such as the leaders and followers, and the structurally balanced and unbalanced nodes. Then, a hierarchical structure decomposition can thus be developed for signed networks considering both the leading roles and structural balance properties of nodes such that all nodes are classified into four subgroups, namely, structurally balanced leaders, structurally balanced followers, structurally unbalanced leaders, and structurally unbalanced followers. For the clarity, we denote these four node subsets as B∩L, B∩F, U ∩L, and U ∩F,respectively. The specific decomposition of all nodes and the interaction flows among four node subsets are illustrated in Fig. 1. We can clearly see from Fig. 1(b) that the structurally unbalanced followers are able to acquire information from all nodes in other node groups, whereas the structurally balanced followers can only receive information from structurally balanced leaders (for detailed explanations, see [105]). Several helpful properties subject to the structure decomposition framework can be revealed in the following lemma. Fig. 1. The decomposition of nodes and the interaction flows among four node subsets [105]. Lemma 7:For any signed digraph G, it holds: 1) L ≠∅; 2) B ∩L=∅⇔B=∅⇔det(L)>0; 3) B ∩L ≠∅⇔B ≠∅⇔det(L)=0. Proof:We can prove this lemma based on [105, Lemmas 3 and 4]. ■ With Lemma 7, a general result for the dynamic behaviors of the signed network (2) subject to any topology condition can be established. Theorem 4([105,Theorem 1]):For the signed network (2)associated with any signed digraph G, all nodes converge with their converged states θi,i∈Infulfilling or equivalently, Remark 3:In Theorem 4, a novel viewpoint for the behavior analysis of signed networks is exploited through revealing the influences brought by the different roles of nodes. It is clear to see that the structurally balanced nodes, especially structurally balanced leaders, dominate the dynamic evolutions of all nodes in signed networks. To be specific, all nodes converge within the convex hull spanned by the structurally balanced leaders’ converged states and their symmetric states. It thus provides a more specific characterization for the dynamic behaviors of the signed network (2) in contrast to the bipartite containment tracking result in Theorem 3. Next, we present an example to illustrate the dominant role of structurally balanced leaders for general signed networks without specific connectivity and structural balance properties. Example 1:Let the signed network (2) be related to a signed digraph G shown in Fig. 2. Based on the hierarchical structure decomposition framework, it is easy to derive that Fig. 2. (Example 1) A signed digraph G without specific connectivity and structural balance properties. and thus that the signed network (2) does not have any specific connectivity and structural balance properties. We perform the simulation of the signed network (2) with the initial condition Fig. 3. (Example 1) The state evolution of the signed network (2) related to the signed digraph in Fig. 2. under which its state evolution is plotted in Fig. 3. From Fig. 3,we can see that the structurally unbalanced leaders all converge to zero such that the stability is established and the structurally balanced leaders cluster such that each leader group achieves bipartite consensus. In addition, for all the followers regardless of their structural (un)balance properties,they converge inside the zone spanned by the converged states of leaders, especially the structurally balanced leaders. This clearly determines the leading roles of the structurally balanced leaders and coincides with the results in Theorem 4. Particularly given the quasi-strong connectivity property,the following results can be directly deduced from Theorem 4. Corollary 1:Let the signed network (2) be associated with a quasi-strongly connected signed digraph G. Then, the signed network (2) realizes 1) bipartite consensus if and only if B =V; 2) interval bipartite consensus if and only if ∅≠B ⊂V (or B ≠∅ and U ≠∅); 3) stability if and only if B =∅. In Corollary 1, a more specific description of the dynamic behaviors is given for quasi-strongly connected signed networks compared with that in Theorem 2. For interval bipartite consensus, the impact index refers to the number of nodes that reach agreement with root nodes in modulus, which actually reflects the influences of root nodes on all other nodes. The calculation of the impact index can be implemented in the presence of the structure decomposition framework, and we provide it in the theorem below. Theorem 5([105,Theorem 4]):Let G be quasi-strongly connected. The impact indexμof the root nodes in the signed network (2) fulfills That is, µ=|B| is equivalent to the number of structurally balanced nodes in G. In Theorem 5, the equivalence of the impact index and the number of the structurally balanced nodes is revealed, which verifies the dominant roles of the structurally balanced nodes.Since the impact index may help to estimate the disagreement of signed networks and to more precisely describe the dynamic behaviors of nodes, it is significant to obtain its accurate value. However, the behavior analysis approaches in the previous two subsections are not effective for the calculation of the impact index. Therefore, the structure decomposition-based behavior analysis approach has its own unique advantages. In the following, we give an example to more clearly show the equivalence between the impact index and the number of the structurally balanced nodes. Example 2:Consider the signed network (2) associated with a quasi-strongly connected signed digraph G in Fig. 4, where the leader (or root node) group {v1,v2,v3} is strongly connected and structurally balanced, and there simultaneously exist structurally balanced followers (or non-root nodes){v4,v5,v6}and a structurally unbalanced follower (or non-root node) {v7}. Based on Corollary 1, the signed network (2)realizes interval bipartite consensus. We depict the state evolution of the signed network (2) in Fig. 5, where the initial condition is given by We can see from Fig. 5 that not only the structurally balanced leaders but also the structurally balanced followers finally have the same state moduli, namely, they reach bipartite consensus, whereas the structurally unbalanced followers converge within the converged states of structurally balanced nodes. As a result, the impact index of the structurally balanced leaders (or root nodes) satisfiesµ=|B∩L|+|B∩F|=6, which illustrates the results in Theorem 5. Fig. 4. (Example 2) A quasi-strongly connected signed digraph G. Fig. 5. (Example 2) The state evolution of the signed network (2) related to the signed digraph in Fig. 4. In real world scenarios, the interactions among nodes generally change over time, which renders the fixed topology no longer applicable. In this section, we further aim at analyzing the disagreement behaviors of signed networks subject to more general time-varying topologies. The close relations between signed and unsigned networks are disclosed based on the state transition matrix-based analysis approach, which helps to build the complete behavior analysis framework for signed networks under specific switching topologies. The disagreement behaviors for signed networks under general time-varying topologies are also briefly discussed. Let a signed network consisting ofnnodes be associated with a time-varying signed digraph G(t). Under the Laplacian flow, the dynamics of the signed network can be described by wherex(t) is the state vector of all nodes,L(t) is the Laplacian matrix of G(t) , andt0≥0 is the initial time. In contrast with(2), the signed network (5) is not a linear time-invariant system any longer but becomes a linear time-varying system such that the eigenvalue analysis of the Laplacian matrix is not effective for exploring the dynamic behaviors of (5).Moreover, due to the existence of antagonistic interactions,the behavior analysis of time-varying signed networks is not easy to be implemented by the stochastic matrix theory, which has been successfully applied to that for time-varying unsigned networks [21], [22], [27]. As a consequence, it is necessary to develop new approaches for the behavior analysis of the time-varying signed network (5). The change of network topologies may lead to more complicated disagreement behaviors for signed networks,including the fluctuation behaviors. In the following, we introduce some meaningful fluctuation behaviors for the signed network (5) (see also [61], [64]). Definition 7:The signed network (5) achieves A popular idea to cope with the time-varying signed network is to build the connections between it and its induced unsigned networks. Then, the existing behavior analysis results of time-varying unsigned networks are applicable for developing those of time-varying signed networks. Motivated by [54], a lifting approach is commonly adopted, which transforms the behavior analysis problem of signed networks to that of related twice enlarged unsigned networks. This equivalent transformation is realized by seeking the relation between the structural balance property of signed networks and the connectivity property of unsigned networks (For detailed behavior analysis results by the lifting approach, the reader can refer to [54], [57], [59]). It is worth mentioning that the development of the lifting approach may require the digon sign-symmetry condition. To overcome this drawback,another way to build the connections of signed and unsigned networks is to adopt the state transition matrix-based approach. These two approaches all utilize the separation idea of cooperative and antagonistic interactions. This subsection mainly focuses on how to develop the essential connections of signed and unsigned networks by resorting to the state transition matrix-based approach. Since (5) is a linear time-varying system, we can solve it asx(t)=Φ(t,t0)x(t0) with Φ (t,t0) being its state transition matrix.DenoteΦ−L|A(t)|(t,t0)asthestatetransitionmatrixof an inducedunsignednetworksubjecttoan unsigned digraph with the adjacency matrix | A(t)|≥0. From [21], Φ−L|A(t)|(t,t0)≥0 is a stochastic matrix. Next, we provide a theorem to build the connectionbetween Φ(t,t0)andΦ−L|A(t)|(t,t0). Theorem6:For anyt≥t0, Φ(t,t0)andΦ−L|A(t)|(t,t0) can be,res pectively,decomposedinto and where Φeven(t,t0)≥0 , ∀t≥t0and Φodd(t,t0)≥0, ∀t≥t0are nonnegative matrices in the form of and In addition, Φ (t,t0) can be bounded by Φ−L|A(t)|(t,t0) as Proof:See the proofs of [61, Theorems 1 and 2]. ■ It shows in Theorem 6 that Φ (t,t0) can actually be viewed as the difference of two nonnegative matrices, the sum of which is the state transition matrix of an unsigned network related to|A(t)|. Consequently, the connections of signed and unsigned networks are found in the sense of the state transition matrices. We may benefit from (6) and (7) to explore dynamic behaviors of the signed network (5). In addition, by further noticingthe fact thatΦ−L|A(t)|(t,t0)isastochasticmatrix, we can directly deducefrom(8)that //Φ(t,t0)//∞≤1, ∀t≥t0. This guarantees that the system (5) is uniformly stable, i.e.,//x(t)//∞≤//x(t0)//∞, ∀t≥t0, which provides an essential premise for the emergence of some nondivergent disagreement behaviors of the signed network (5). We can further exploit Theorem 6 to get another relation of signed and unsigned networks based on also the state transition matrices of them, which is given in the theorem below. Theorem 7([61,Theorem 3]):Let Then Ψ(t,t0)=Φ−LA(t)(t,t0) is the state transition matrix of a linear system with the state matrix as −LA(t), whereLA(t)is exactly the Laplacian matrix of an unsigned digraph with the nonnegative adjacency matrix given by It is clear thatA(t) is a nonnegative matrix derived from the adjacency matrix A(t)∈Rn×n, which is the adjacency matrix of an unsigned digraphG(t)=(V,E(t),A(t)) with 2nnodes derived from the signed digraph G(t). From Theorems 6 and 7, we see that the signed digraph G(t) is related closely to the unsigned digraphs G(|A(t))| a ndG(t). It is worth emphasizing that the proposal of Theorems 6 and 7 never imposes any requirement on topologies, such as the connectivity property,the structural balance property, and the digon sign-symmetry property. As a consequence, the connections built for signed and unsigned networks in Theorems 6 and 7 are applicable for any time-varying signed networks with the system dynamics given by (5) regardless of any topology condition. The switching topology is a special case of the time-varying topology, which admits that the interactions among all nodes switch at some instants and remain unchanged in the rest of time. The interactions among nodes in a signed network subject to the switching topology can generally be represented by a switching signed digraph G(t) (see Section II-B). We have revealed the close relations between the signed network and its associated unsigned networks from the view of state transition matrices in Theorems 6 and 7. To proceed, we further apply Theorems 6 and 7 to address the behavior analysis problem for the signed network (5) in the presence of switching topologies. Becausex(t)=Φ(t,t0)x(t0),∀t≥t0,t0≥0, it is only required to explore the dynamic evolution of the state transition matrix Φ(t,t0). Next, we present the convergence property of Φ(t,t0) with respect to jointly strongly connected signed digraphs. Lemma 8:Let Assumption 1 hold and G(t) be jointly strongly connected. Then l imt→∞Φ(t,t0)=D1nvT(t0)D(respectively, l imt→∞Φ(t,t0)=0) , ∀t0≥0 with an exponentially fast speed,whereD∈Dandv(t0)≥0satisfyDA(t)D=|A(t)|andvT(t0)1n=1,if and onlyifG(t) iss.s.b.(respectively, s.s.ub.). Proof:For the s.s.b. signed digraph G(t), Φeven(t,t0) and Φodd(t,t0)converge exponentially fast such that For the s.s.ub. signed digraph G(t), Φeven(t,t0) andΦodd(t,t0)converge exponentially fast such that By inserting (10) and (11) into (6), we can directly obtain the convergence results in Lemma 8. For more details, the reader can refer to [61, Lemmas 5 and 7]. ■ With Lemma 8, the dynamic behaviors of the jointly strongly connected signed network (5) can be revealed. Theorem 8([61,Theorem 4]):Let Assumption 1 be satisfied and G (t) be jointly strongly connected. Then for anyt0≥0, the signed network (5) establishes bipartite consensus(respectively, stability) exponentially fast if and only if G (t) is s.s.b. (respectively, s.s.ub.). In Theorem 8, necessary and sufficient conditions are provided on the bipartite consensus and the stability for the jointly strongly connected signed network (5) under switching topologies, which shows that the simultaneous structural balance and unbalance are two mutually exclusive conditions for the bipartite consensus and the stability, respectively. In addition, it yields that given the ergodicity property, the switching signed networks exhibit the similar disagreement behaviors to those of fixed signed networks under the strong connectivity property. However, for switching signed networks without any particular connectivity property, more complex disagreement behaviors may emerge in contrast with fixed signed networks. Given any switching signed network, all the nodes can be classified into two groups, that is, the union leaders and the union followers, which are dependent on the roles of nodes in the union signed digraphGσp. Without loss of generality, we assume that G(t) haskunion leader groups withminodes in theith union leader group. Let us denote the subgraphs of G (t) overand over F∪as GLi(t)={VLi,ELi(t),ALi(t)}, ∀i∈Ikand as GF(t)={VF,EF(t),AF(t)}, respectively. From the definition of the union leader, it is clear that GLi(t), ∀i∈Ikis uniformly strongly connected without any neighbor. Under this classification, the Laplacian matrix of G(t)can be given in the form of whereLL(t)=diag{LL1(t),LL2(t),...,LLk(t)} withLLi(t) as the Laplacian matrix of GLi(t), ∀i∈Ik[,LF(t)] is the Laplacian matrix of GF(t), and AFL(t)=∈R(n−m)×mwithm=miand(t)=a(i+m)j(t) , ∀i∈In−m,j∈Im. Then,by the Peano-Baker series expression of Φ(t,t0) (see [108]),Φ(t,t0)can also be described in a special form as where Φ−LL(t)(t,t0)andΦ−LF(t)−∆|AFL(t)|(t,t0)denotethestate transition matricessubjectto thestatematrices−LL(t)and−LF(t)−∆|AFL(t)|, respectively, and Besides, Φ−LL(t)(t,t0) is actually in a block-diagonal form as whereΦ−LLi(t)(t,t0) isthe statetransitionmatrixsubject to the statematrix −LLi(t),∀i∈Ik. Basedon (12),the dynamic behaviors of the signed network(5) subject toany switching signed digraph G (t) can be disclosed in the following theorem. Theorem 9([64,Theorem 1]):Let Assumption 1 hold. Then the signed network (5) establishes bipartite containment fluctuation. Furthermore, all union leaders converge (uniformly and exponentially fast) such that each union leader group realizes either bipartite consensus or uniform asymptotic stability. Remark 4:In Theorem 9, it validates that all union leaders converge but may have different converged states, whereas the union followers may fluctuate instead of converging inside the bound formed by the converged states and the symmetric states of the union leaders, which reflects a class of leadercontained phenomena. Compared with the disagreement results for fixed signed networks in Section III, the fluctuation behaviors for signed networks are revealed in Theorem 9,which may show a stronger disagreement among nodes. This indicates that the change of topologies may be one of the important inducements for the fluctuation of signed networks and may result in the stronger disagreement of nodes. It is also worth emphasizing that the development of Theorem 9 does not impose any condition on the switching topologies except for the ergodicity property. Hence, the results in Theorem 9 are applicable for any possible switching signed network under the Laplacian-type model, in spite of the connectivity property, the structural balance property, and the digon signsymmetry property. As a particular case, we can derive a quasi-interval bipartite consensus result straightforwardly from Theorem 9 for jointly quasi-strongly connected signed networks. Corollary 2:Let Assumption 1 hold. Then the signed network (5) related to a jointly quasi-strongly connected signed digraph G(t) achieves quasi-interval bipartite consensus(respectively, stability) if and only if G(t) admits an s.s.b.(respectively,s.s.ub.)subgraph Gr(t), where Gr(t) is the subgraphof G(t) over. Section III-C shows that the structure decomposition framework for fixed signed networks may help to more specifically characterize the disagreement behaviors of them.Similar results also hold for switching signed networks. From Section II, we can divide the nodes of switching signed digraphs into four separate groups, which is implemented based on the structural balance properties and leading roles of them. Consequently, four classes of roles can be identified for the nodes of switching signed networks, i.e., the simultaneously structurally balanced union leaders, the simultaneously structurally balanced union followers, the simultaneously structurally unbalanced union leaders, and the simultaneously structurally unbalanced union followers. For the clarity,denote these four node subsets as B∩∩L∪, B∩∩F∪, U∩∩L∪,and U∩∩F∪, respectively. Obviously, these four node subsets are time-invariant, i.e., the role of each node is fixed, even though the considered signed network is time-varying.Analogously to Lemma 7, it follows that L∪≠∅ and B∩∩L∪=∅ if and only if B∩=∅. Thanks to the structure decomposition of switching signed networks, we can more specifically describe the disagreement behaviors for the signed network (5) in the following theorem. Theorem 10([106,Theorem 1]):Let Assumption 1 hold.For the signed network (5) related to any switching signed digraph G (t), all union leaders converge such that In comparison with Theorem 9, the dominant roles of the simultaneously structurally balanced union leaders are further validated in Theorem 10. Besides, it is also implied that if there exist no simultaneously structurally balanced union leaders, then the stability is accomplished for the signed network (5). For a jointly quasi-strongly connected signed network, a more specific behavior analysis result can be further provided in the following theorem. Theorem 11:Let Assumption 1 hold and G (t) be jointly quasistrongly connected. Then the signed network (5) realizes 1) bipartite consensus if and only if B∩=V; 2) quasi-interval bipartite consensus if and only if∅≠B∩⊂V (i.e., B∩≠∅ and U∩≠∅), where the impact indexμsatisfies µ =|B∩∩L∪|+|B∩∩F∪|; 3) uniform asymptotic stability if and only if B∩=∅. Proof:This theorem can be developed directly from [106,Theorems 3 and 4]. ■ Remark 5:From Theorem 11, it is disclosed that for jointly quasi-strongly connected signed networks, if the same structural balance properties hold for all nodes, the convergence behaviors are possible to be realized, under which they have the same state moduli. Otherwise, the fluctuation behaviors may emerge such that only simultaneously structurally balanced nodes reach bipartite consensus and other nodes either converge or fluctuate inside the bound spanned by the simultaneously structurally balanced nodes’ converged states. This implies that the inconsistency of the structural balance properties for nodes may be a potential factor for the emergence of the fluctuation. Next, an example is given to illustrate the results in Theorem 10 for general switching signed networks. Example 3:We consider the signed network (5) with respect toatime-varying{ signeddigrap}hG(t) switchingamongthree candidates=Gσ1,Gσ2,Gσ3given inFig. 6for anyt≥0.Weadopt thefollowing switchingrule: suchthat Assumption 1 holds.Itis clear thatthe unionof Gσ1,Gσ2,and Gσ3yieldsthe signeddigraph shownin Fig. 2, which directlyleads tothat Fig. 6. (Example 3) Three candidates for a switching signed digraph G (t). Therefore, the signed network (5) does not possess any specific connectivity and structural balance properties.Besides,wecanverifythat for thesigneddigraphGσ1,{v3,v5,v6}arefollowers and{v9,v11,v17}areleaders,which are inconsistent with the role identification of the union leaders and followers for G(t). The similar role inconsistency also appearsin Gσ2andGσ3.Inthefollowing,wewill exhibitthe dominant roles ofunionleaders.We takethe sameinitial condition as that in Example 1 to perform the simulation,under which we depict the state evolution of the signed network (5) in Fig. 7. From Fig. 7(b), we can see that two simultaneously structurally balanced union leader groups achieve bipartite consensus, respectively, whereas the simultaneously structurally unbalanced union leaders establish stability. In addition, Fig. 7(a) indicates that not all union followers converge and both simultaneously structurally balanced and unbalanced union followers are finally limited by the converged states of simultaneously structurally balanced union leaders and their symmetric states. This clearly shows the validity of the results in Theorem 10. The discrete-time counterpart of the Laplacian-type model(5) has also been widely studied, which can similarly be coped with by resorting to the lifting approach or the state transition matrix-based approach. For more details of the behavior analysis results of the discrete-time model with respect to switching topologies, the reader can refer to [56], [57], [61]. For signed networks under switching topologies, they can be regarded as linear time-varying systems composed of several linear time-invariant systems, thanks to which we can explore their dynamic behaviors by the segmentation.However, for the general time-varying signed networks with interactions among nodes changing at every time instant, the behavior analysis approaches for switching cases may not be effective anymore. To deal with the general time-varying signed networks, a state modulus-based analysis approach is exploited in [55], based on which this subsection mainly introduces the disagreement behaviors of general time-varying signed networks. From Section IV-A, we can verify that //Φ(t,t0)//∞≤1,∀t≥t0. Consequently, //x(t)//∞≤//x(t0)//∞, ∀t≥t0holds such that the signed network (5) is uniformly stable under general time-varying topologies. Hence, the boundedness of the states of all nodes can be ensured. In the following analysis, let the initial time of (5) bet0=0. From (5), the dynamics of theith node are in the form of wherexi(t), ∀i∈Inis the state of theith node. Let the state modulus of each node be denoted by Xi(t)=|xi(t)|, ∀i∈Inand it satisfies (see [55, Lemma 10]) where θij(t) = sign(xi(t))sign(xj(t))sign(ai j(t)) ∈{−1, 0, 1},∀i,j∈In. By exploring the dynamic evolution of the system(13), the dynamic behaviors of the signed network (5) can be obtained, which are given in the theorem below. Theorem 12:Letai j(t), ∀i,j∈Inbe bounded for anyt≥0.If G(t) is uniformly strongly connected, then the signed network (5) realizes modulus consensus. Further, if G(t) is s.s.b., then the signed network (5) realizes bipartite consensus. Proof:The proof of Theorem 12 can be implemented by leveraging the ordering permutation technique for Xi(t). For more detailed proof processes, the reader can refer to the proof of [55, Theorem 2 and Lemma 4]. ■ Fig. 7. (Example 3) The state evolution of the signed network (5) whenG(t)switches among the signed digraphs G σ1, G σ2 , and G σ3 in Fig. 6. It reveals in Theorem 12 that the uniform strong connectivity results in the modulus consensus of time-varying signed networks, which gives a class of agreements on the state modulus. When the uniform strong connectivity can not be guaranteed, it is challenging to exploit the dynamic behaviors of the time-varying signed network (5) without the simultaneous structural balance, since the similar structure decomposition framework as that for switching signed networks is hard to be established. Hence, the necessary conditions for the modulus consensus are difficult to be determined owing to the complicated change of topologies. Furthermore,it is also not easy to distinguish the necessary and sufficient conditions for the bipartite consensus and the stability even given the uniform strong connectivity. There have been reported few behavior analysis results for the general timevarying signed networks. But it is clear that more complex disagreement behaviors may emerge in general time-varying signed networks compared with switching ones. With Theorems 13 and 14, the complete framework is built for the behavior analysis of the time-varying signed network(5) under the cut-balance assumption. This mainly attributes to the good properties implied in the cut-balance condition such that only two classes of topology conditions possibly emerge in time-varying signed networks. However, it is worth pointing out that owing to the limitations generated by the cutbalance assumption, only the convergence behaviors may occur given the general time-varying topologies. In comparison, the more complicated disagreement behaviors, including the fluctuation, can emerge in the time-varying signed network (5) without the requirement of the cut-balance property,the analysis of which may be much more challenging.Besides, for the discrete-time counterpart of the Laplaciantype model (5) subject to general time-varying topologies,there actually is no essential difference between it and that for the switching signed networks. In the previous two sections, we have explored the dynamic behaviors of static signed networks, whose interactions among nodes are represented by either constants or time-varying real numbers. Nevertheless, in the practical scenarios, the dynamic interactions may possibly exist in signed networks, that is, the communication channels among nodes may be in the presence of transfer functions or linear time-invariant systems. Network systems having dynamic interactions can be commonly seen,particularly in thermal processes for rooms of buildings, large scale systems with interconnected storage components, and load frequency control networks of electric power grids[114]–[116]. The dynamic networks have many potential applications. For example, they are applicable for solving the PageRank problem, in which the dynamic interactions may be beneficial to filter or deal with the negative hyperlinks, like those from spammers [117], [118]. Because of the existence of dynamic interactions, the signed digraphs shown in Section II are not effective any longer to describe topologies of dynamic signed networks. In this section, an introduction of the dynamic signed digraphs is provided to represent the interactions among nodes in dynamic signed networks, under which the disagreement results for dynamic signed networks subject to the Laplacian flow are presented together with their applications. The main results in this section were originally proposed in [92], and the reader can refer to it for more details. A dynamic signed digraph can be in the presence of a triple G(A(s))={V,E,A(s)} with V as the node set, E as the edge set, and A(s)=[ai j(s)]∈Cn×nas the adjacency matrix. It is satisfied thatai j(s)≠0,∃s∈C ⇔(vj,vi)∈E; andaij(s)=0,otherwise. (vj,vi)∈E hints that the communication channel from the nodevjto the nodeviis equipped with a transfer functionai j(s) such that the information ofvjreceived byviis processed through a linear time-invariant system. The notions of the neighbor, path, and connectivity of G (A(s)) are defined in a similar way as those of the fixed signed digraph. Forai j(s)≠0, we, respectively, denote the leading coefficients of its numerator polynomial and its denominator polynomial asNLC(ai j(s))≠0andDLC(aij(s))≠0. Then,wecanfurther provide thedefinitions ofthecoefficientmatrix Acoefand the nominal (transfer function) matrix Anom(s) of A (s) as and It is easy to verify that A(s)=Acoef◦Anom(s) such thatai j(s)=(s) , ∀i,j∈In. Clearly, the following equivalent relations hold: Consider a signed network withnnodes, which is relevant to a dynamic signed digraph G(A(s)). Theith node has the single-integrator dynamics fulfilling wherexi(t)∈R andui(t)∈R are the state and the control input of theith node, respectively. Through the Laplace transform,the frequency domain description of (14) can be given as whereXi(s) andUi(s), respectively, denote the Laplace transforms ofxi(t) andui(t), andxi(0) is the initial state of theith node. Then, we follow the nearest neighbor rule to propose a dynamic distributed control protocol for the system (15) as which, substituted into (15), yields whereLA(s)is theLaplacianmatrix of G(A(s)),X(s)=[X1(s),X2(s),...,Xn(s)]T, andx(0)=[x1(0),x2(0),...,xn(0)]T.We aim at exploring disagreement behaviors of the dynamic signed network (16) by exploiting properties of G(A(s)). To proceed, the weakly strictly positive real (WSPR) property is first introduced (see also [119, Definition 2.5]). Definition 8:A (rational) transfer functionh(s) is said to have the WSPR property ifh(s) is analytic for alls∈and Re(h(jω))>0, ∀ ω ∈R is satisfied. The WSPR property ensures that the rational transfer functionh(s) is stable and is a positive real number under any positive real variables. Then, we attach the WSPR property to each interaction channel of G(A(s)) and define a property (P)for G (A(s)) as follows: Proof:We can verify theresultsin thislemma by resorting to [92,Lemmas 2 and3 andCorollary 1].■ Based on Lemma 9, we can implement the behavior analysis for the dynamic signed network (16). If the poles of all entries in [sI+LA(s)]−1lie in C<0or C≤0with only one zero pole, the final value theorem is applicable for the dynamic signed network (16) [120]. LetQ(s)=[sI+LA(s)]−1, the pole distribution of which is presented in the lemma below. Lemma 10:Let G(A(s)) be undirected, namely,AT(s)=A(s), ∀s∈C holds. If G (A(s)), ∀s∈C having the property (P)is connected and s.b. (respectively, s.ub.), then the poles of all entries inQ(s) belong to C≤0with only one unique zero pole(respectively, C<0). Proof:The straightforward consequences of [92, Lemmas 5 and 6]. ■ Thanks to Lemma 10, the following theorem can be established to disclose the disagreement behaviors of the undirected dynamic signed network (16). Theorem 15([92,Theorem 1]):Let G(A(s)) be undirected,connected and have the property (P). Then the signed network(16) realizes 1) bipartite consensus if and only if G(A(s)) is s.b.Furthermore, it holds: whereD∈D satisfiesDAsgnD=|Asgn|; 2) stability with limt→∞x(t)=0 if and only if G(A(s)) is s.ub. Remark 6:The disagreement behaviors are given in Theorem 15 for signed networks under undirected dynamic topologies, which clearly indicates that the bipartite consensus and stability correspond to the structural balance and unbalance properties of their associated dynamic signed undirected graphs. An interesting fact implied in Theorem 15 is that thanks to the property (P) of G(A(s)), the dynamic interactions among nodes do not dominate the final converged states of all nodes, which are the same as those of the static signed network (2) associated with G(Asgn). It is worth noting,however, that the dynamic interactions impact the dynamic evolution processes of dynamic signed networks, such as the convergence rate and the transient behaviors. This hints that we may benefit from the design of the proper dynamic controllers rather than the static controllers to enhance the transient performances of signed networks subject to the same convergence behaviors. Remark 7:The dynamic signed network (16) includes many common signed networks as special cases. For example, (16)can represent the dynamics of the hybrid static and dynamic signed network, in which there simultaneously exist the static and dynamic interactions among nodes. As another example,if(s)=1,∀aij(s)≠0holds,then G(A(s))collapsestoa fixedsigneddigraph G(Acoef),which clearly hastheproperty(P). Consequently, not only the results in Theorem 1 developed for the signed network (2) subject to fixed undirected topologies are extended, but also an alternative frequency domain approach is provided for the behavior analysis of the signed network (2). We give two examples to show the bipartite consensus and stability results in Theorem 15. Example 4:We consider the signed network (16) related to a dynamic signed graph G (A(s)) in Fig. 8(a). The static signed graph G(Asgn) subject to the sign-indicator matrix Asgnof G(A(s))is also given in Fig. 8(b). We can see from Fig. 8(b)that G(Asgn) is connected and s.b. such that G(A(s)) is also connected and s.b. Further, it is easy to verify that the property(P) is also satisfied for G(A(s)). According to Theorem 15,the bipartite consensus can be achieved for the signed network(16). We depict the state evolution of the signed network (16)with respect to the dynamic signed graph G(A(s)) in Fig. 9(a)under the initial condition which indicates that all nodes in the signed network (16) reach agreement on modulus such that limt→∞|xi|=1.375, ∀i∈I8,namely, the bipartite consensus is realized. Furthermore, the state evolution of the signed network (16)subject to the static signed graph G(Asgn) is provided in Fig. 9(b), for which the same initial condition as that subject to the dynamic signed graph G (A(s)) is employed. In Fig. 9(b),the bipartite consensus is guaranteed with limt→∞|xi|=1.375,∀i∈I8. Consequently, we can deduce that the same converged states can be established for the signed network (16)under both the dynamic signed graph G(A(s)) and the static signed graph G (Asgn), whereas the transient performances for them are different as shown in Figs. 9 (a) and 9 (b). This implies that the dynamic interactions do not influence the final converged states of all nodes except for the transient evolution processes of them. Fig. 8. (Example 4) An s.b. dynamic signed graph G(A(s)) and its related s.b. static signed graph G (Asgn). Fig. 9. (Example 4) The state evolutions of the signed network (16) under the s.b. signed graphs in Figs. 8(a) and 8(b). Example 5:Let the signed network (16) be associated with a dynamic signed graph G(A(s)) given in Fig. 10(a), whose relevant static signed graph G(Asgn) is shown in Fig. 10(b).Because G(Asgn) is connected and s.ub., G(A(s)) is also connected and s.ub. Besides, the property (P) holds for G(A(s)). Then, we implement the simulation for the signed network (16) with respect to the dynamic signed graph G(A(s))under the same initial condition as that in Example 4,where its state evolution is depicted in Fig. 11(a). Fig. 11(a)shows that the signed network (16) accomplishes stability,which illustrates the effectiveness of the results in Theorem 15. For comparison, we admit the same initial condition to perform the simulation for the signed network (16) subject to the static signed graph G(Asgn) with its state evolution given in Fig. 11(b). We can see from Fig. 11(b) that the stability is realized, which reflects the same convergence behavior as that subject to the dynamic signed graph G (A(s)). When the directed dynamic signed networks are taken into account, there may exist more diverse disagreement behaviors. Even given the property (P), the divergence behaviors may still emerge, which brings many difficulties to the behavior analysis of them. Hence, the behavior analysis results for the directed dynamic signed network (16) have only been investigated under some particular cases, for which the reader can refer to [92], [93]. Fig. 10. (Example 5) An s.ub. dynamic signed graph G(A(s)) and its related s.ub. static signed graph G (Asgn). Fig. 11. (Example 5) The state evolutions of the signed network (16) under the s.ub. signed graphs in Figs. 10(a) and 10(b). Behavior analysis results for the dynamic signed network(16) can be not only directly applied to fixed signed networks or hybrid static and dynamic signed networks but also extended to deal with signed networks with high-order dynamics or communication delays, which will be introduced in detail in this subsection. Consider an oscillator network subject to double-integrator dynamics and theith node has the dynamics as withk>0 as the damping coefficient, andxi(t)∈R andui(t)∈Ras the state and control input of theith node. Let the system (17) be relevant to a fixed signed graph G(A).According to the nearest neighbor rule, a typical distributed control protocol is employed as Through the Laplace transform, (17) and (18) can be described in a frequency domain formulation as wherex(0) andx˙(0) are the initial conditions, andX(s) is the Laplace transform ofx(t)=[x1(t),x2(t),...,xn(t)]T. We can particularly take which obviously has the property (P). Then, (19) can also be described in the form of Theorem 16([92,Theorem 2]):Let G (A) be undirected and connected. The system (19) realizes 1) bipartite consensus if and only if G(A) is s.b. Moreover,it holds: whereD∈D satisfiesDAD=|A|; 2) stability with limt→∞x(t)=0 and limt→∞x˙(t)=0 if and only if G (A(s)) is s.ub. The system (19) is actually a second-order signed network.From Theorem 16, we can see that by certain transformations,the second-order signed networks can be described in the form of dynamic signed networks such that they can be investigated under the framework of the dynamic signed networks. From another perspective, it also implies that the existence of the dynamic interactions increases the order of their related closed-loop systems because they create a class of dynamic feedback controllers. Even though we only present the connections of dynamic signed networks and second-order signed networks, the behavior analysis results and their corresponding analysis ideas in Theorem 15 may also be applicable for the behavior analysis of signed networks with general high-order dynamics. As another application, the behavior analysis results given for dynamic signed networks may help analyze the behaviors of signed networks with communication delays. We consider a signed network with its dynamics given by (14) and let it be relevant to a fixed signed graph G(A), whose communication channels among nodes are equipped with the time delay τ ≥0.By the nearest neighbor rule, the distributed control protocol for this signed network can be given as which, together with (14), can result in a frequency domain description in the form of wherex(0) is the initial state andX(s) is the Laplace transform ofx(t)=[x1(t),x2(t),...,xn(t)]T. Clearly, (21) falls into the framework of (16) with A(s)=e−τsA. Next, we benefit from Theorem 15 to discuss the dynamic behaviors of the signed network (21). Theorem 17([92,Theorem 3]):Let G (A) be undirected and connected. The system (21) achieves modulus consensus if and only if τ ∈(0,τˆ), where τˆ=π/[2λn(LA)] with λn(LA) as the maximum eigenvalue ofLA. In particular, the system (21)realizes 1) bipartite consensus if and only if G(A) is s.b. Moreover,it holds: whereD∈D satisfiesDAD=|A|; 2) stability with limt→∞x(t)=0 if and only if G(A(s)) is s.ub. From Theorem 17, it is indicated that the time delays have little effects on dynamic behaviors of signed networks as long as they are small enough. By comparing (21) with (16), we may see that the time delays can be regarded as the dynamic components of communication channels such that they may be more effectively coped with based on the frequency domain approaches. Furthermore, it is worth mentioning that the more general case that different communication channels possess different time delays is also involved in the framework of the dynamic signed network (16). Hence, it may be well studied by leveraging the techniques for dynamic signed networks. In this paper, we have introduced the disagreement behaviors for signed networks in the presence of both cooperative and antagonistic interactions. Given the single-integrator linear dynamics, two classes of topologies have been discussed, that is, the static topology and the dynamic topology,where the previous one includes both the fixed topology and the time-varying topology. For the signed networks with respect to fixed signed digraphs, three different behavior analysis approaches have been developed such that similar disagreement behaviors have been disclosed from different perspectives. For the signed networks with time-varying topologies, we have presented a state transition matrix-based approach to establish the relations between them and their relevant unsigned networks, based on which a complete behavior analysis framework has been given for switching signed networks. In addition, some disagreement behaviors for general time-varying signed networks have also been briefly introduced. For the dynamic signed networks with adjacency weights in the form of transfer functions, we have shown the specific descriptions and characteristics of them, by which their disagreement behaviors have further been revealed relying on the properties of their related static signed graphs. Moreover, their applications to the behavior analysis of signed networks under high-order dynamics or communication time delays have also been proposed. Note that owing to the simple dynamics of signed networks under fixed topologies, the complete behavior analysis framework and results have been developed. By contrast, for time-varying signed networks, the disagreement behaviors subject to only specific switching topologies have been revealed, whereas concerning general time-varying topologies, the disagreement behaviors are barely known except for those given the uniform strong connectivity. Therefore, the general time-varying signed networks are worth further investigation such that more diverse disagreement behaviors can be disclosed. Moreover, due to the complex characteristics of dynamic signed networks, only the undirected cases have been systematically explored. However, the directed dynamic signed networks may be more common in many real scenarios, the disagreement behavior analysis of which is also a valuable issue for further study. In addition, the behavior analysis problems for signed networks with respect to more complicated dynamics, such as the high-order dynamics or the nonlinear dynamics, are interesting and challenging, and they are worth further consideration, especially concerning the different classes of topologies.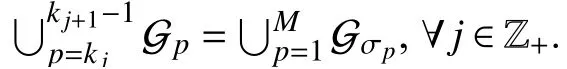
C. Structural Balance Theory

III. LAPLACIAN-TYPE MODEL UNDER FIXED TOPOLOGIES
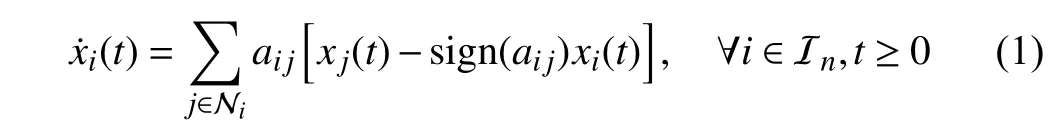
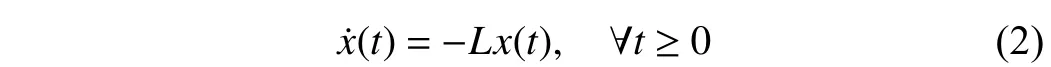
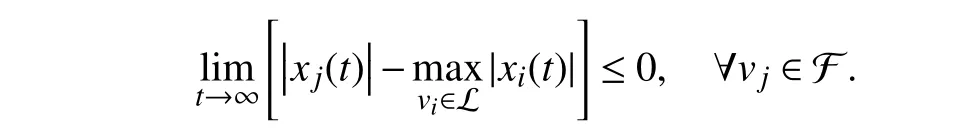
A. Graph-Based Analysis Approach
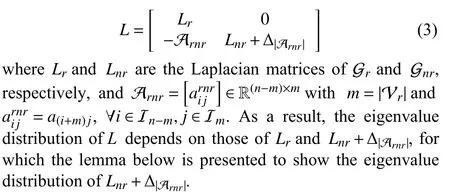

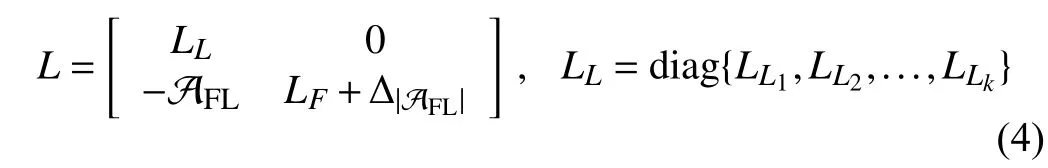
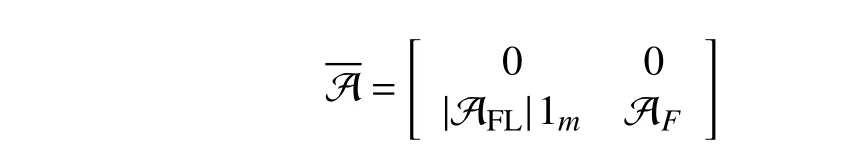
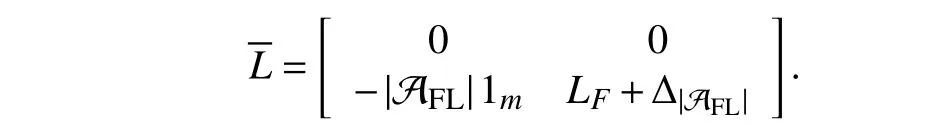
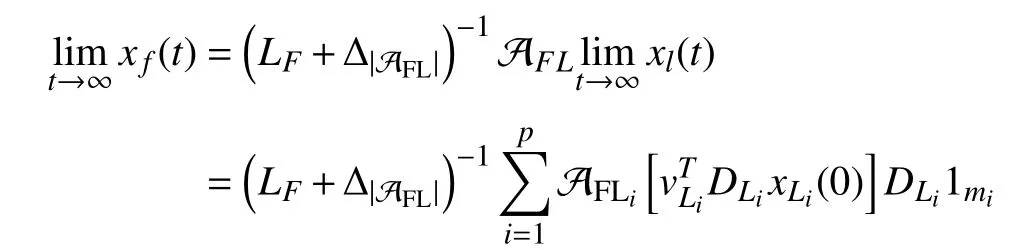
B. M-Matrix-Based Analysis Approach
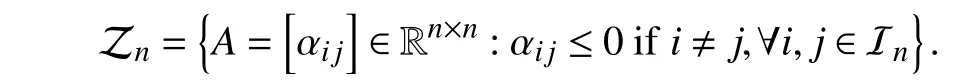
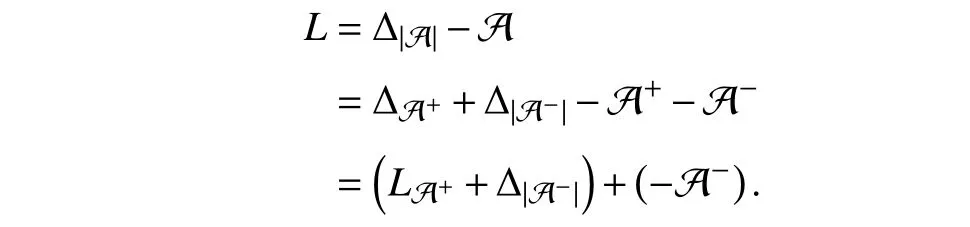
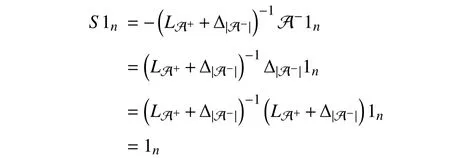
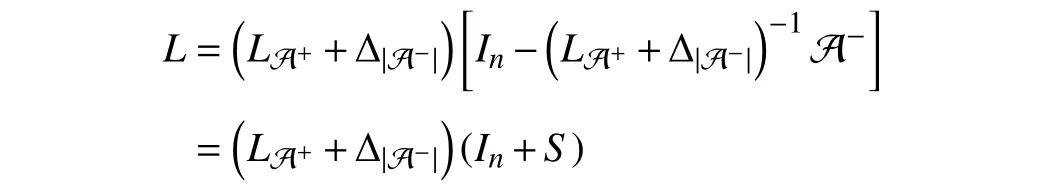
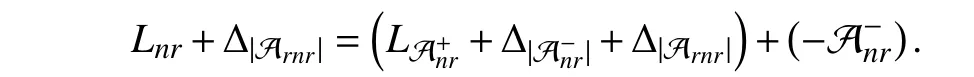
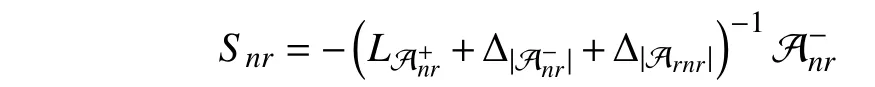
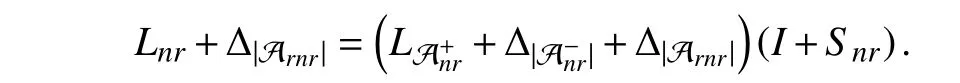
C. Structure Decomposition-Based Analysis Approach
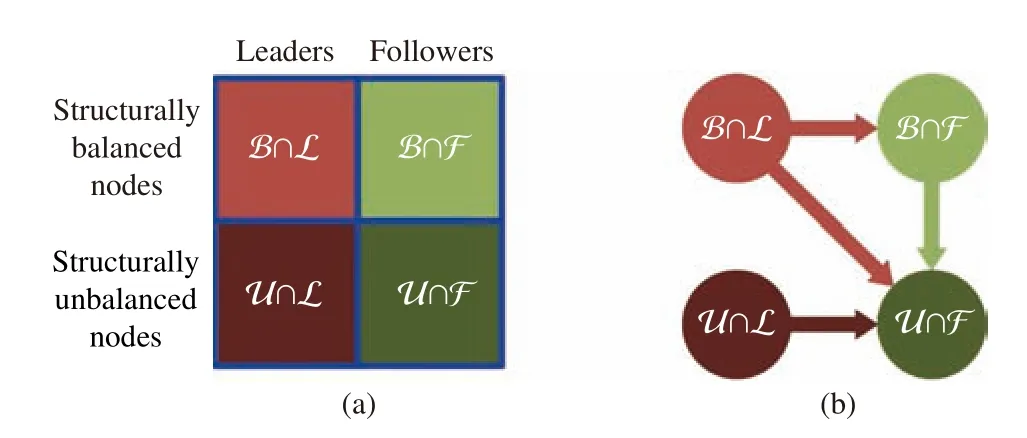
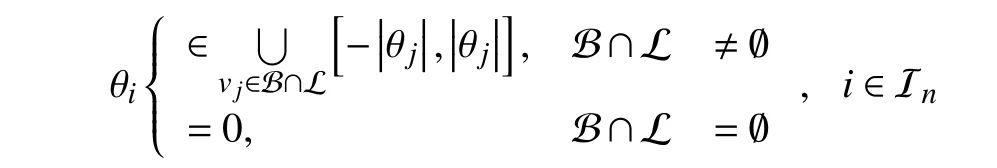
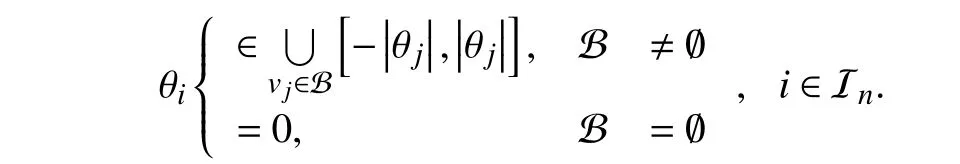
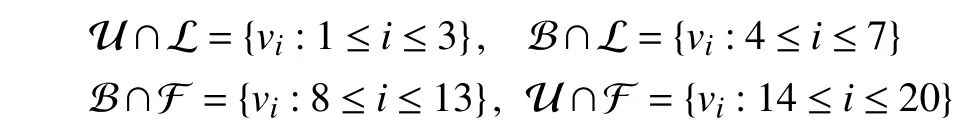
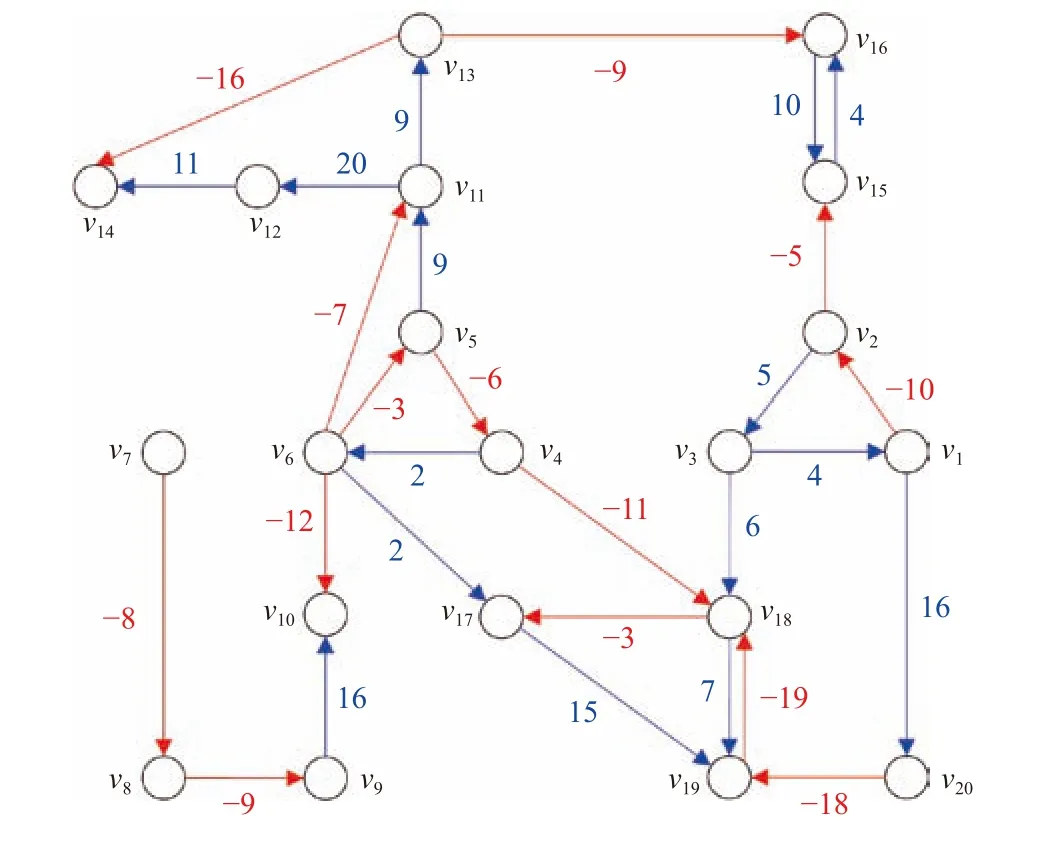
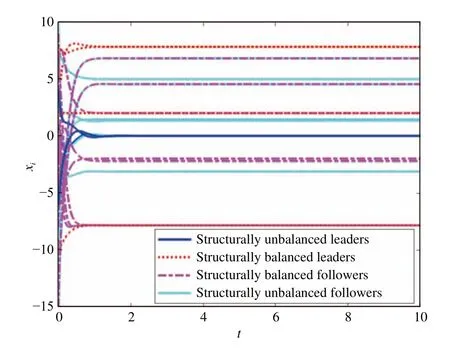
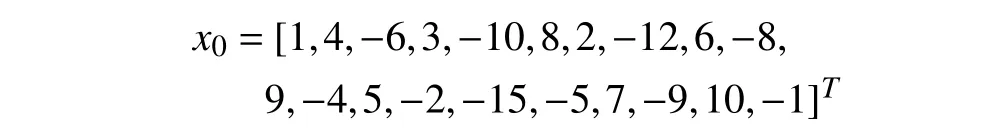
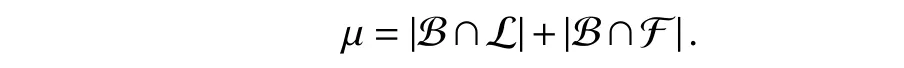
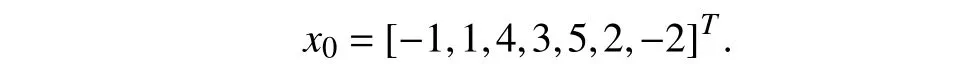
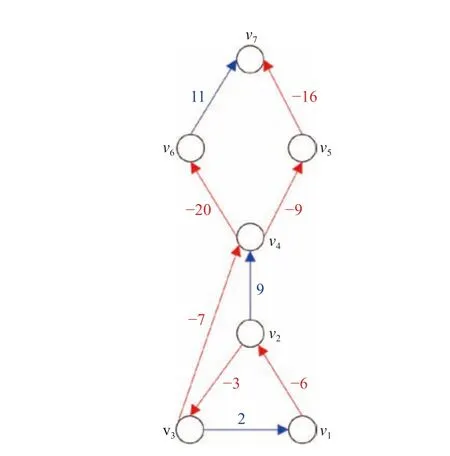

IV. LAPLACIAN-TYPE MODEL UNDER TIME-VARYING TOPOLOGIES
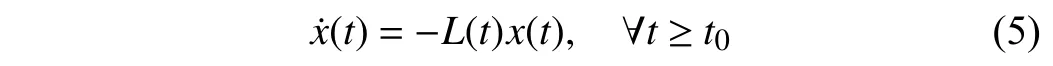

A. Connections of Signed and Unsigned Networks
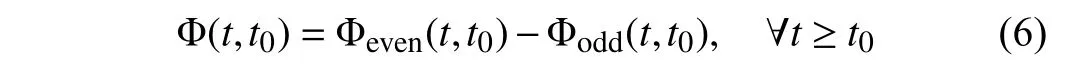
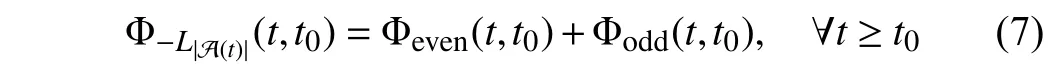
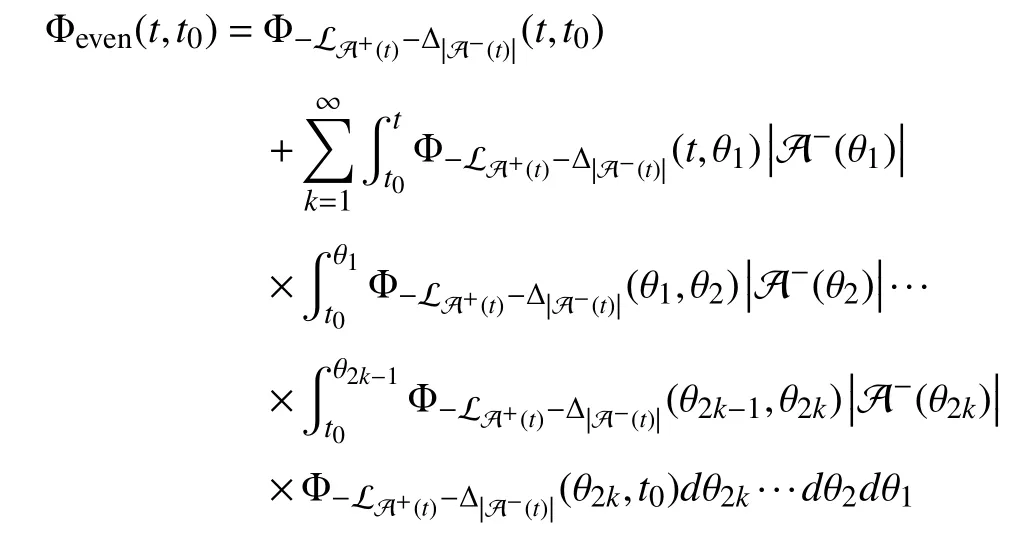
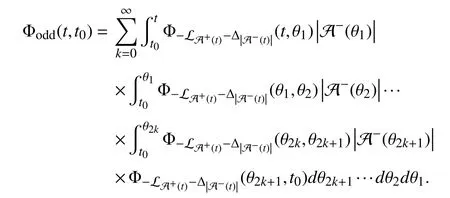
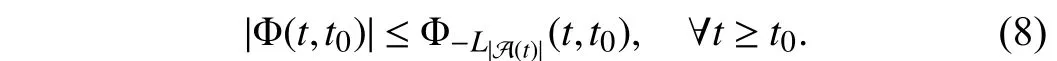
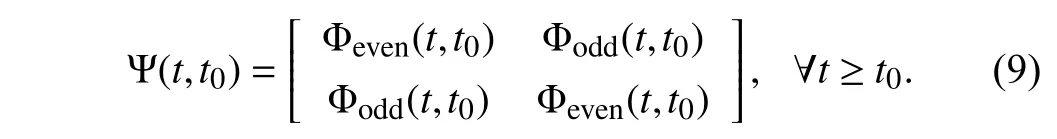
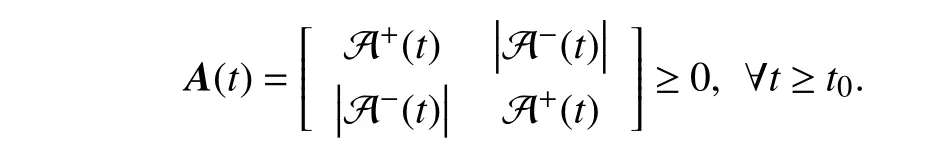
B. Switching Topology
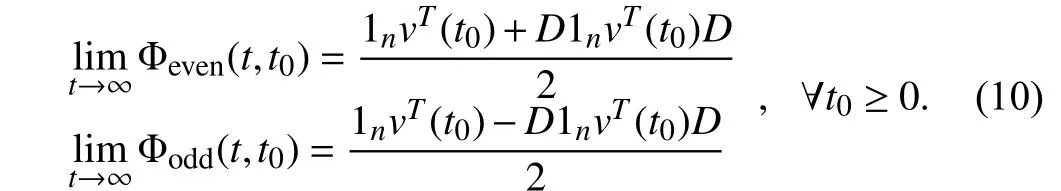
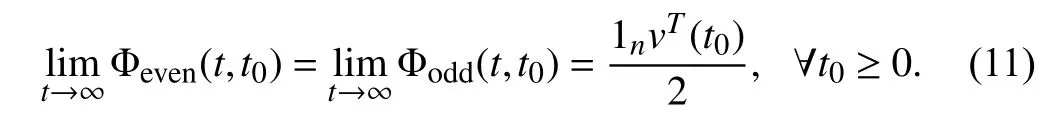
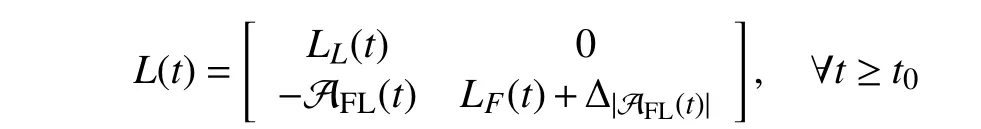
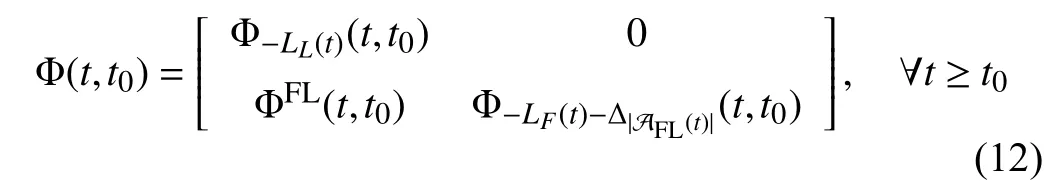
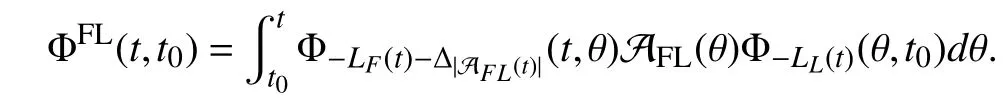
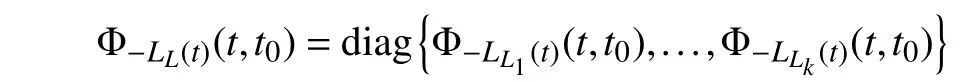
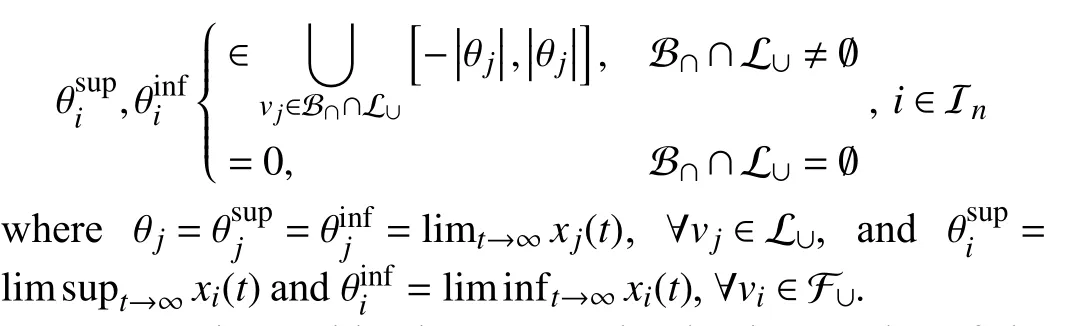
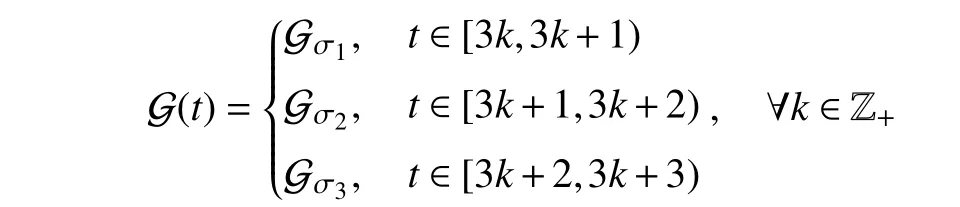

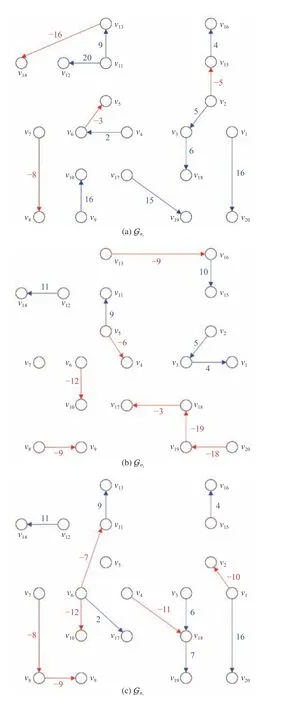
C. General Time-Varying Topology
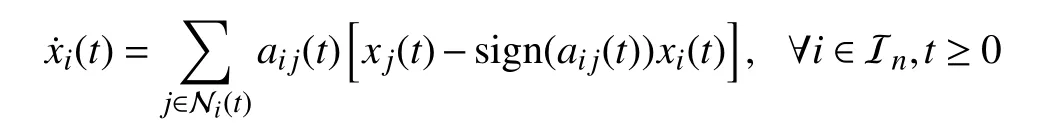
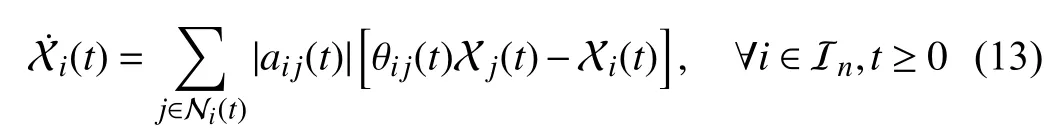
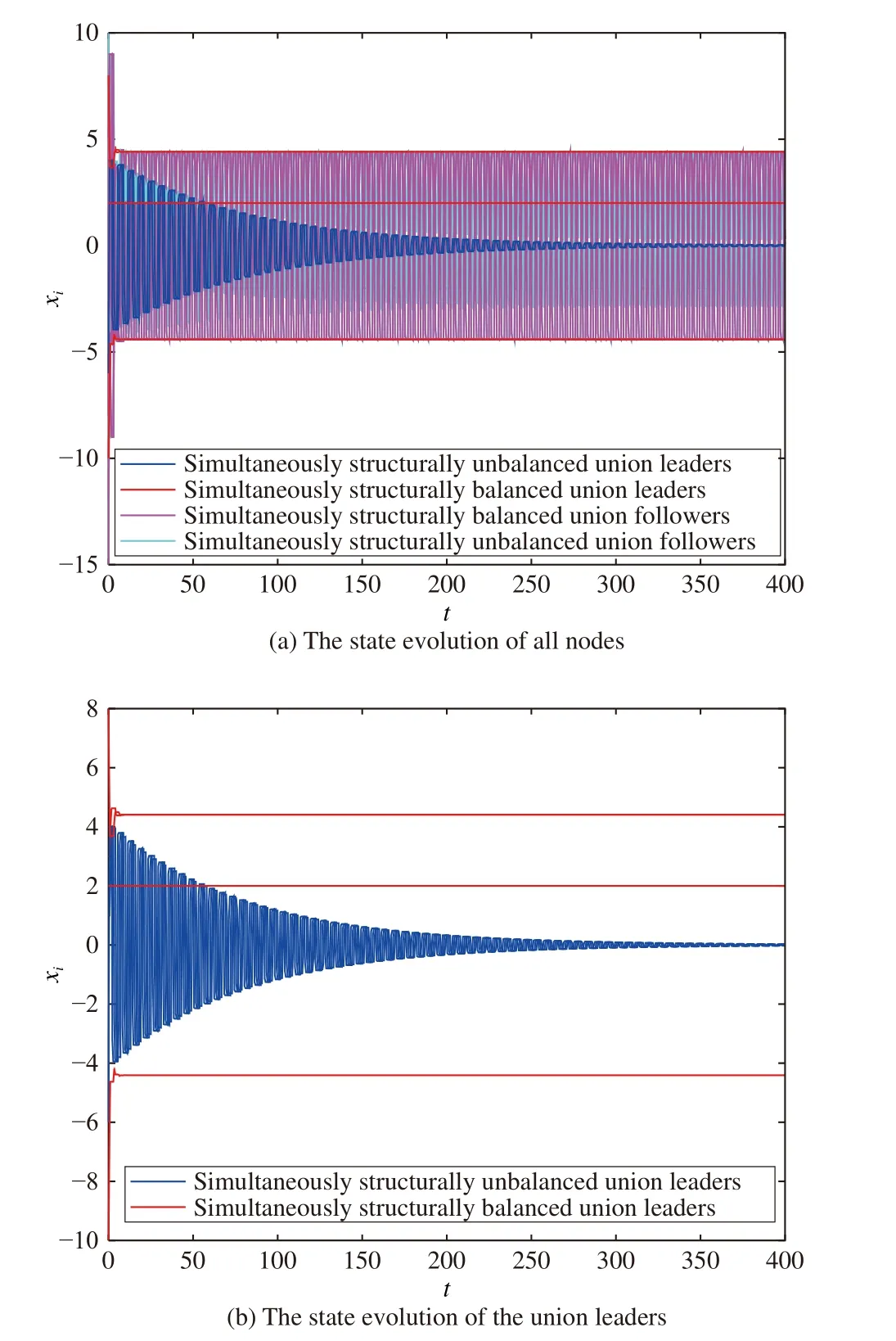


V. DYNAMIC SIGNED NETWORKS
A. Dynamic Signed Digraph
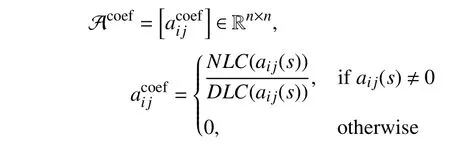
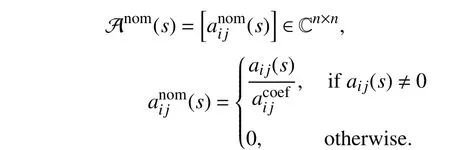

B. Behavior Analysis of Dynamic Signed Networks
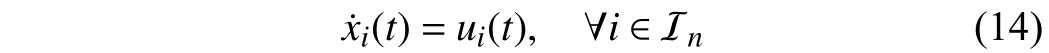
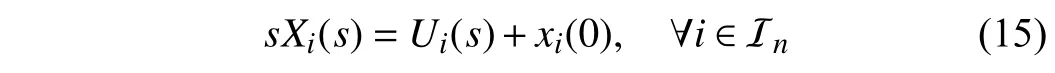
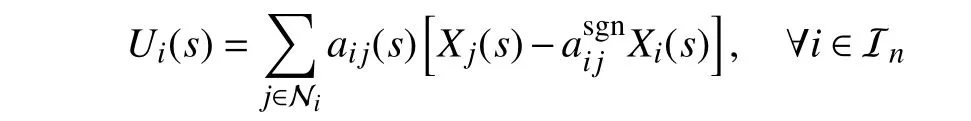
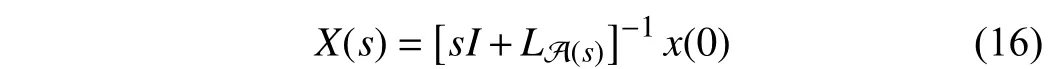
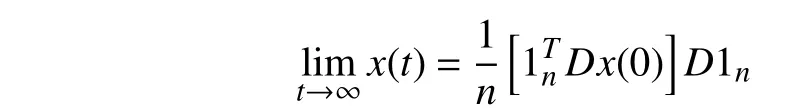
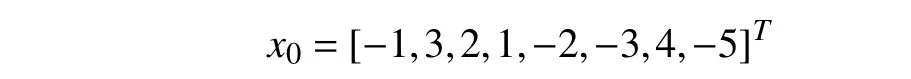
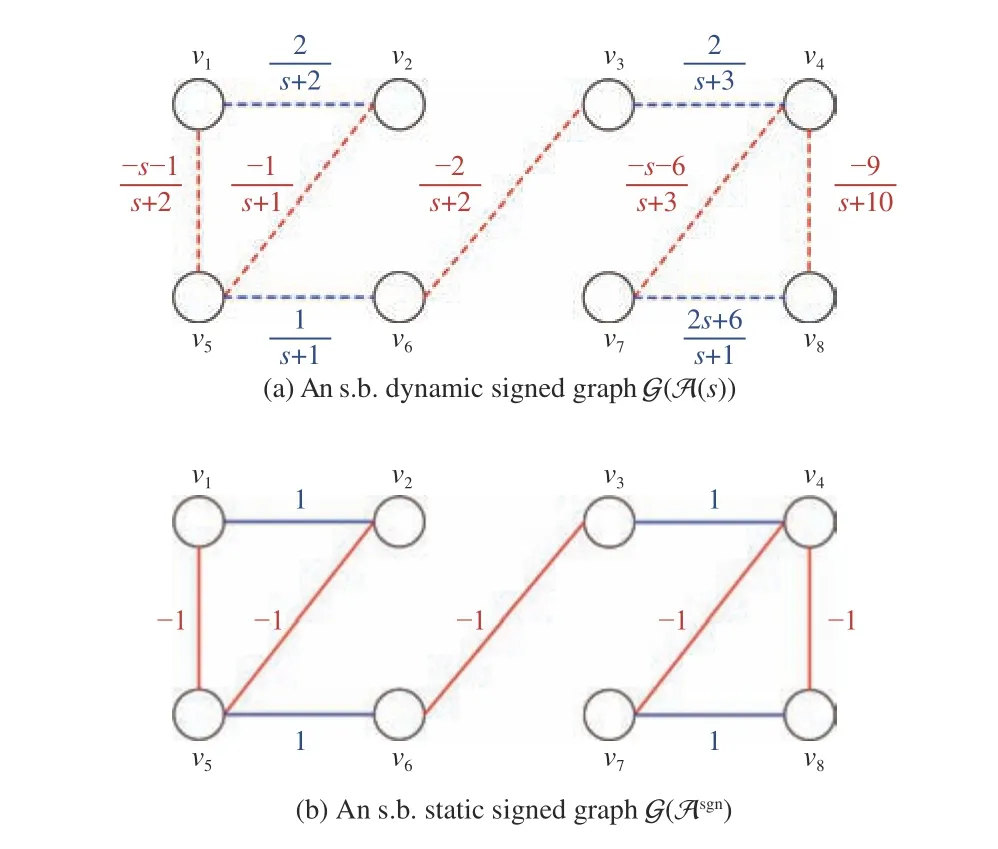
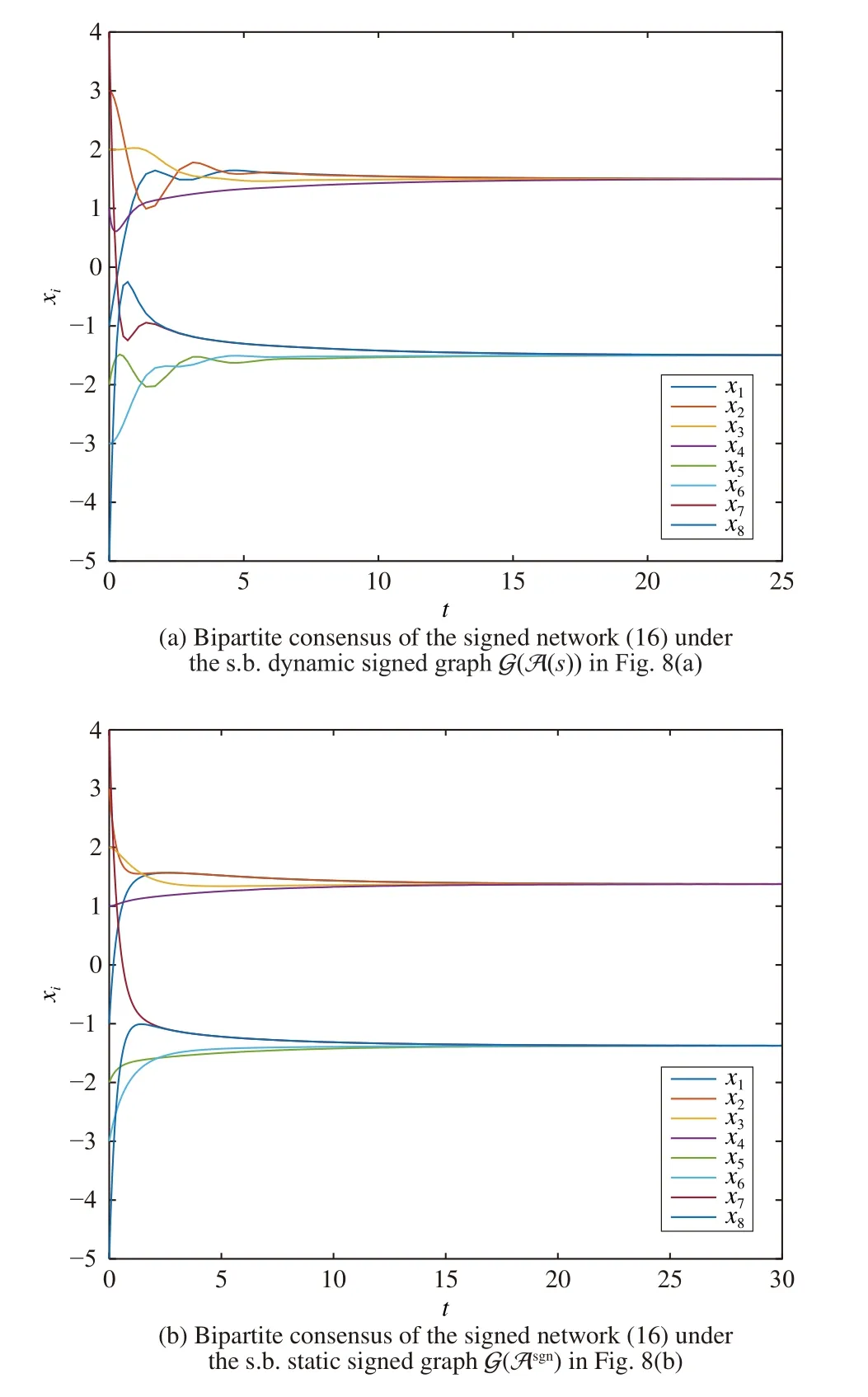
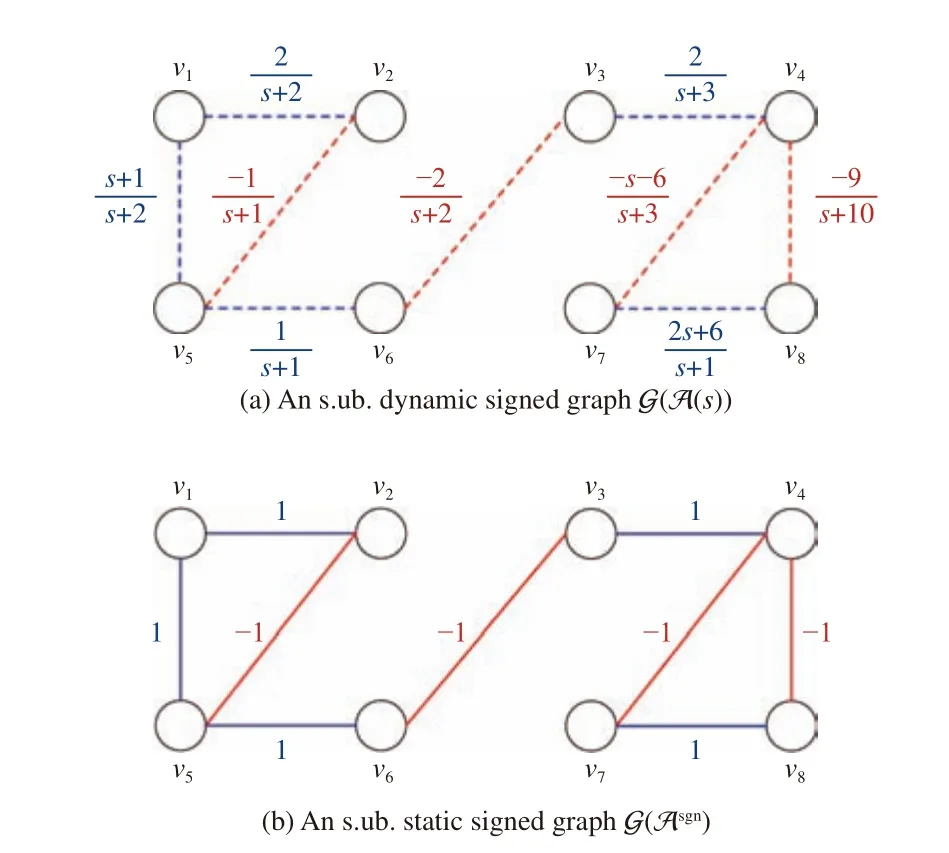
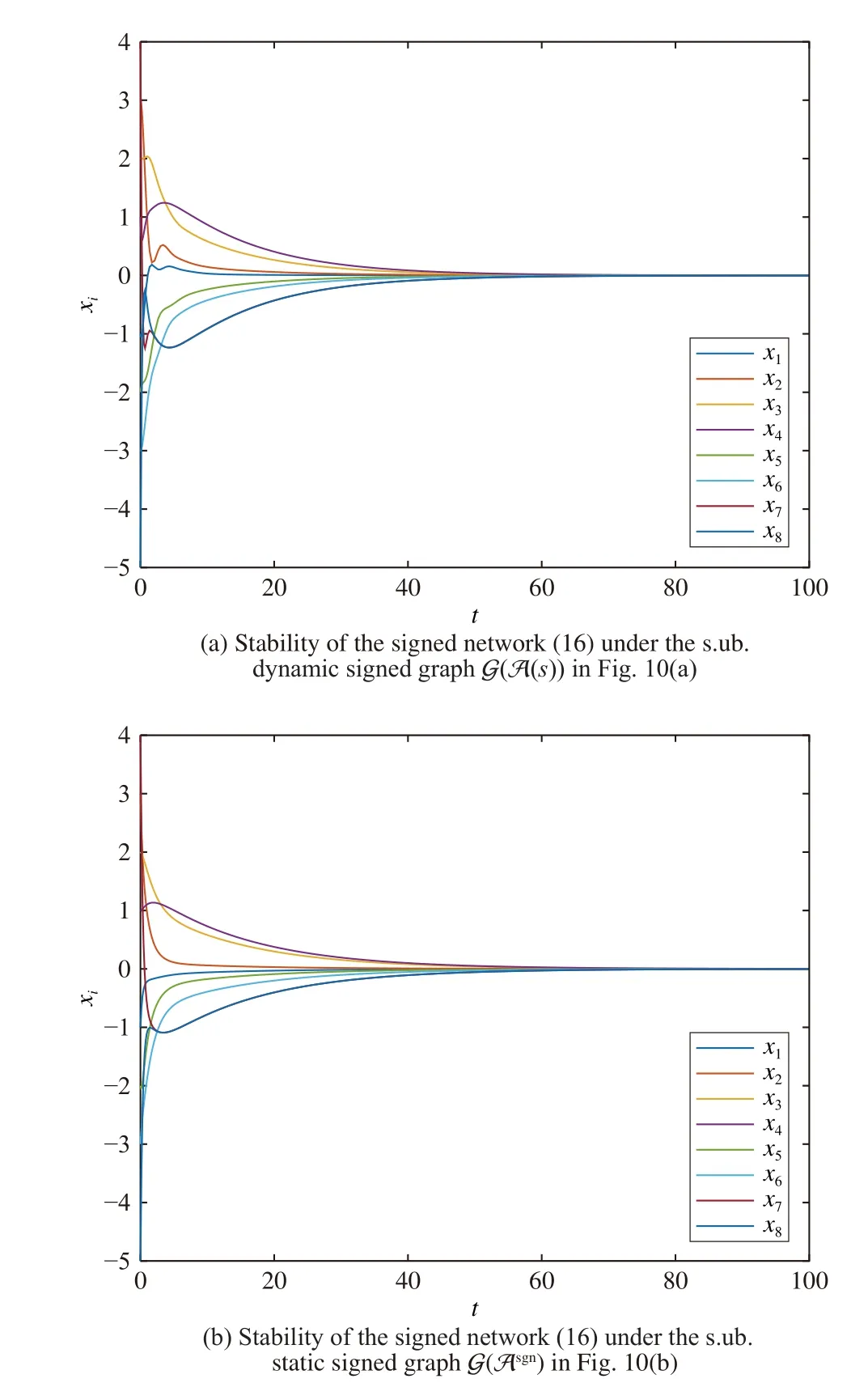
C. Applications
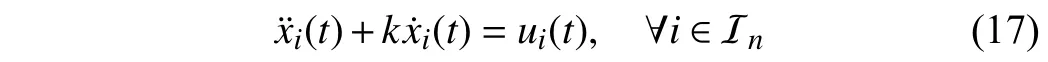
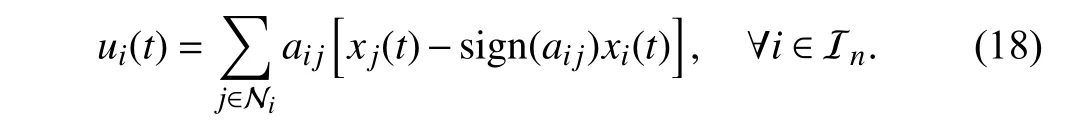
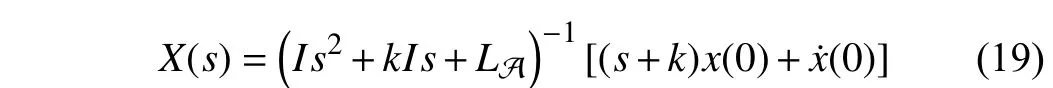
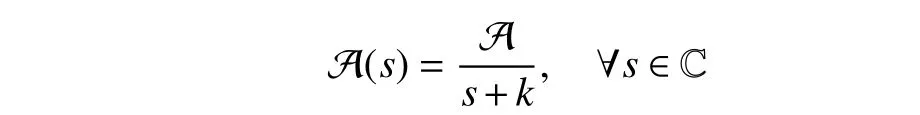
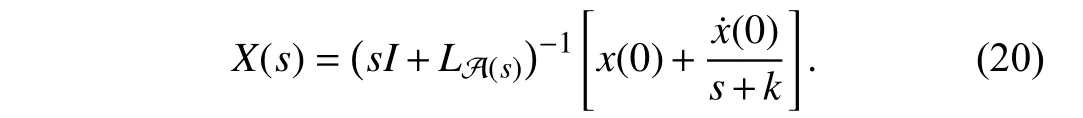
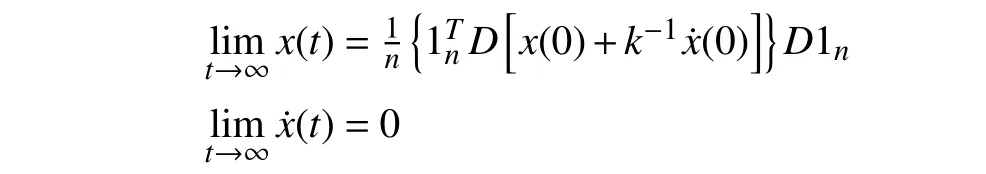
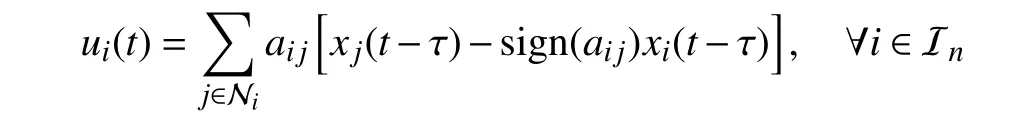
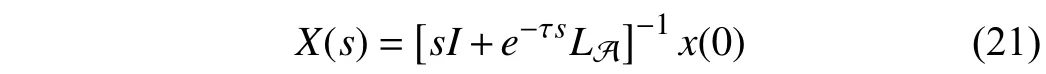

VI. CONCLUSIONS
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- An Overview and Experimental Study of Learning-Based Optimization Algorithms for the Vehicle Routing Problem
- Towards Long Lifetime Battery: AI-Based Manufacturing and Management
- Finite-Time Distributed Identification for Nonlinear Interconnected Systems
- SwinFusion: Cross-domain Long-range Learning for General Image Fusion via Swin Transformer
- Real-Time Iterative Compensation Framework for Precision Mechatronic Motion Control Systems
- Meta Ordinal Regression Forest for Medical Image Classification With Ordinal Labels
