Modeling and Analysis of Matthew Effect Under Switching Social Networks via Distributed Competition
2022-07-18MeiLiuSuibingLiandLongJin
Mei Liu, Suibing Li, and Long Jin,,
Dear editor,
This letter models and analyzes the Matthew effect under switching social networks via distributed competition. A competitive strategy is leveraged to trace the evolution of individuals in social systems under the Matthew effect. In addition, a consensus filter is utilized to decentralize the model with undirected graphs used to describe the interactions among individuals in social networks. Further, a term is added to the dynamic consensus filter to compensate for the influence of the switching of communication networks on the model. In this letter, the convergence of the proposed Matthew effect model is theoretically proved, and simulative experiments are conducted to verify the availability of the model. In particular, this letter points out the state and evolution of each individual in social systems with distributed competition, and the influence of the social environment on the development of individuals is also intuitively displayed.
Introduction:The Matthew effect is essentially a process in which individuals or organizations with development advantages in some fields of social systems further accumulate advantages, which means that the strong get stronger and the weak get weaker, and it exists widely in social systems. Most of the existing work has been devoted to proving the existence of the Matthew effect in a certain field and characterizing it through language. Farys and Wolbring [1] investigate the influence of the Nobel Prize effect on citations based on the case of obtaining the Sveriges Riksbank Prize in Economic Sciences in Memory of Alfred Nobel, and results show that there is a cumulative advantage of the Matthew effect in this field. They estimate a linear panel regression model with the logged number of yearly citations as outcomes, in which the relationship between the Nobel Prize and the number of citations is quantitatively described, and the causal relationship between them is explored, which is devoted to proving the existence of the Matthew effect. In addition, Regarding the impact of journal rankings on the number of citations received by their papers, Drivas and Kremmydas [2] explore the Matthew effect contained therein. Moreover, the Matthew effect has also been widely confirmed in the fields of network science [3], education [4],economics [5], and politics [6], etc.
Agent-based modeling (ABM) adopts computational methods to simulate social phenomena [7], [8]. Through abstracting individuals in the real world into simplified agents and simulating operations and interactions performed by multiple agents simultaneously, complex social processes are reproduced. In this way, a better understanding of social structure, functions, and changes can be obtained, and further, the evolution direction of social systems can be predicted and evaluated [9]. In view of the feasibility and effectiveness of ABM in simulating social phenomena, to investigate the Matthew effect in social systems in depth, a computational model is established in this letter using the ABM technology based on the theoretical research and empirical basis of this social effect. The above-mentioned model simulates the dynamic evolutionary process of social systems under the Matthew effect, from which to obtain guidance on human behaviors and provide optimized solutions for decision-making.
Due to the dynamic nature of social systems, social networks tend to change over time. In addition, changes in interferences from various factors in complex systems may cause switching of social networks. In view of this, when establishing the computational model of social systems under the Matthew effect, it is essential to consider the dynamic communication in social networks. In recent years,many scholars conduct a series of research on the impact of switching in communication networks on the accuracy of models[10]. For instance, in [11], the cooperative output regulation problem of the singular multi-agent system subject to the jointly connected switching networks is examined. Wang and Yang [12] present a cooperative fault-tolerant control method under switching directed networks.
This letter exploits ABM technology for the first time to design a Matthew effect model that can ensure the accuracy and stability of the system under switching social networks. Facing the challenge of how to construct the model accurately, firstly a communication topology is established, and a distributed consensus filter with compensation for switching communication topologies is selected to accurately describe the interactions among agents. Then, competitive strategy is utilized for tracing the influence of the Matthew effect.Finally, the evolutionary behaviors of individuals in social systems are modeled. Through theoretical analyses and numerical simulations, the convergence and effectiveness of the constructed model are verified. Moreover, this letter points out possible application scenarios of the proposed model. The schematic diagram of this letter is shown in Fig. 1.
Problem statement:Under a switching and jointly connected communication topology, the question is how to effectively model the Matthew effect in social systems in a distributed manner.Specifically, under the premise that at least one topology is maintained for a long enough time in all switching time periods,nagents continue to develop with the goal of occupying the monopoly position in their field. Among them,kagents currently occupying development advantages have cumulative advantages and are able to develop themselves rapidly. Ultimately,kagents occupy the monopoly position in the field, and the remainingn-kagents lose.
Preliminary and scheme formulation:
1) Communication topology: Undirected and jointly connected graphs are used to represent social networks, reflecting the interactions among individuals in social systems. Each node in the undirected graph represents an agent (individual, organization, or area in social systems), and the interactions among agents are represented by the adjacency matrix A=[aij]n×nof the undirected graph. In addition, the corresponding communication status is expressed by the Laplacian matrix L=[lij]n×n=diag(A1n)−A where 1nis a vector composed ofnelements with each one being 1.Define the neighbor set of theith agent as Ni. When there is an edge between theith node and thejth node, we call thejth agent the neighbor of theith agent, that is,j∈Ni.
Under these circumstances, theith agent and thejth agent in the social network can communicate with each other directly. If all topologies in the topology series are balanced and the union of all the topologies is connected, then this set of topologies is called jointly connected. It is worth noting that the social network discussed in this work is based on the assumption of joint connectivity.
2) Distributed consensus filter: In social networks, each agent is often unable to know the global information, and they obtain the reference for the next decision-making through concurrent information interaction with their neighbors. To achieve distributed communication, various distributed filters are utilized to decentralize models [13]−[15]. Therefore, in order to better describe the distribution of interactions among individuals in social systems,thereby improving the reliability, usability, and scalability of the model, the distributed consensus filter presented by Freemanet al.[16] is considered
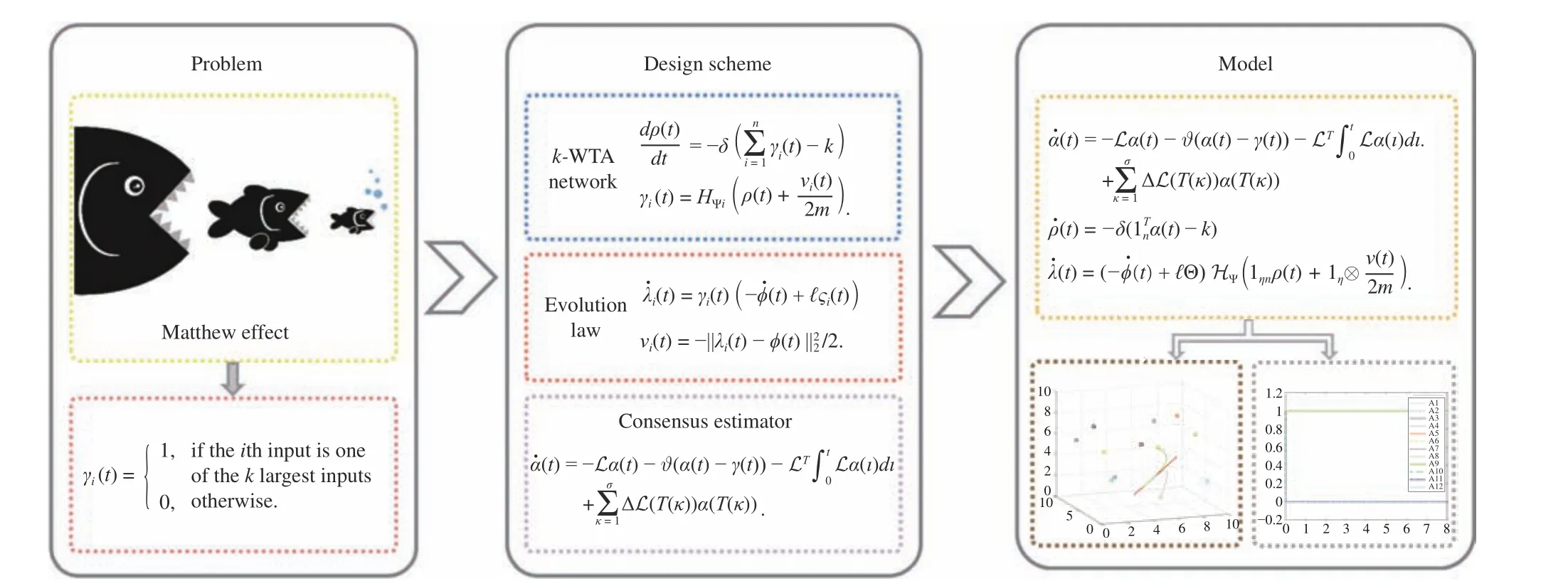
Fig. 1. Schematic diagram of this letter.
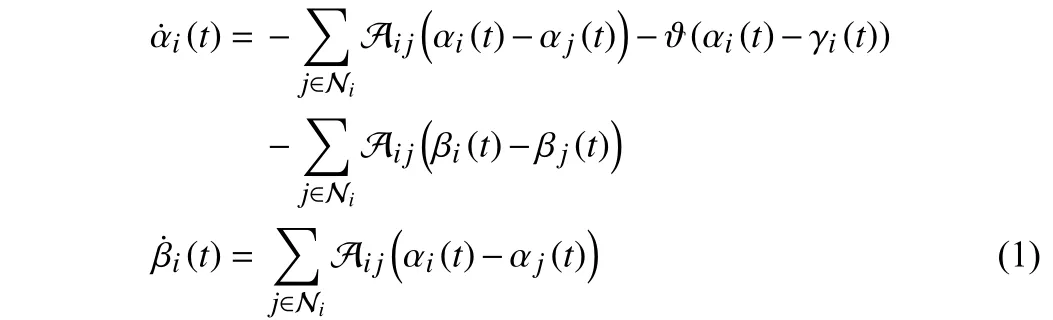
where γi(t)is thesignalfollowedby thefilter;αi(t)isthe decision variable; βi(t)isthe internalestimatorstate;ϑ>0istheglobal estimatedcoefficient.

of which superscriptTrepresents the transpose operation;T(κ)indicates the time at which the κth switching of the communication topology happens;σdenotes the index set of the switch times;△L(T(κ))signifies the difference of the Laplacian matrix before and after timeT(κ). When the topology is fixed, the compensation term remains 0. After each topology switching, the system needs to reconverge to the correct solution in the new state. Therefore, there must be at least one topology to be maintained for a long enough time in all switching time periods to ensure the convergence of the filter [18]. Furthermore, the following theorem holds for switching balanced graphs.

Then, the additional item can be simplified to
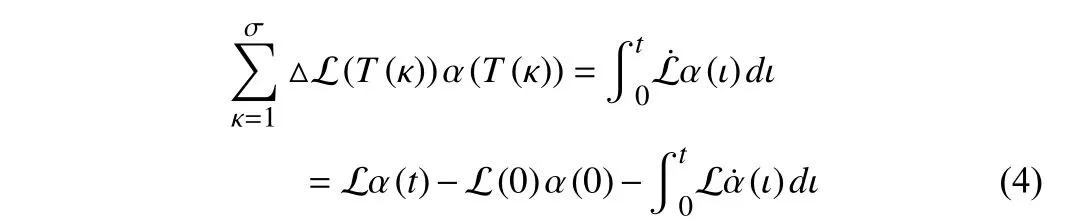
where L (0) and α (0) are the Laplacian matrix and the state value at the initial time, respectively. According to (4), (2) can be reformulated as
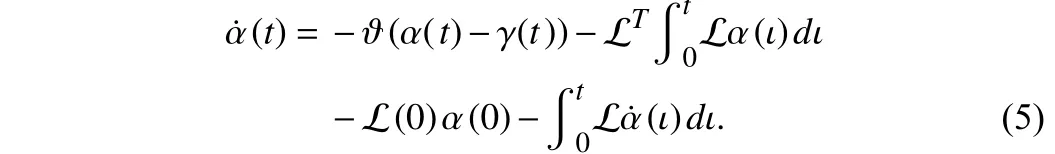
Next, define an auxiliary variable
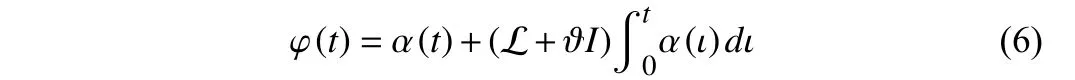
whereIis ann×nidentity matrix and its time derivative is

Matthew effect model:Since the winner-take-all (WTA) competitive strategy is a kind of manifestation of the Matthew effect, the WTA network can be leveraged to control the evolution of agents in social systems under the Matthew effect. A neural network that can select the maximum value from a set of inputs is called a WTA network. As a generalization of WTA,k-winners-take-all (k-WTA)refers to selectingkmaximum values from a set ofninputs, and there have been a lot of related researches [19], [20]. A centralizedk-WTA network [21] is presented by Hu and Wang
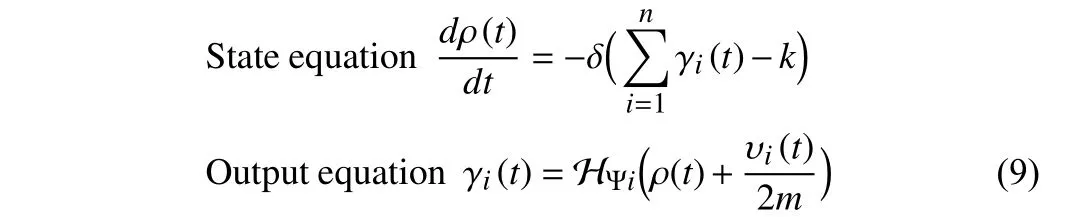
whereυi(t)represents theithinput;γi(t) representstheithoutput;ρ(t)isauxiliaryvariables;δisa positive coefficient relatedtothe convergence rate of the network, and within the allowable range of the hardware and calculation, the larger the value ofδ, the faster the convergence speed of thek-WTA network;mis a constant being
enough small. Fori= 1,...,nand Ψi=[0,1], HΨiis defined as
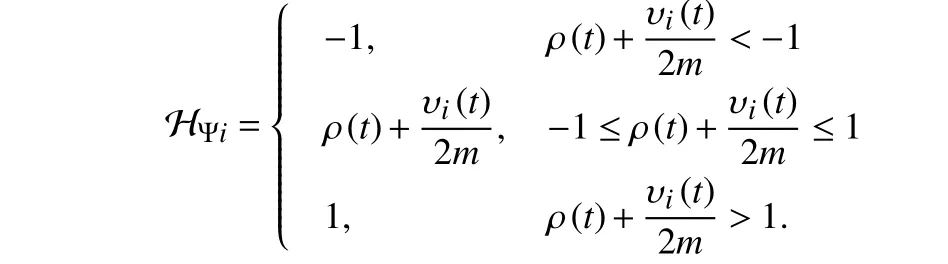
The network (9) can assign the corresponding outputs of theklargest inputs to 1, which is expressed as
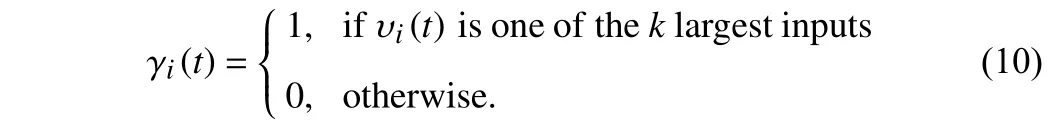
In order to describe the evolutionary behaviors of individuals in social systems, individuals are abstracted into different agents, and the evolution law of each agent is defined as

Substituting the above expression into (11), and organizing obtain
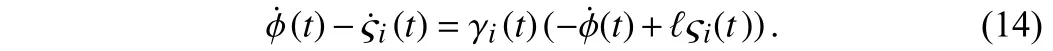
Then, (14) can be transformed into
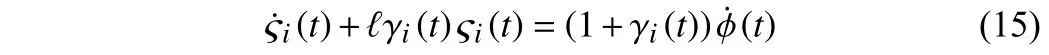
whose solution is

whereηrepresents the dimension of λ(t) and ϕ(t) ; ⊗ is the Kronecker product.
Experiments:Thek-WTA network is exploited to select the dominant individuals in the current social environment, and then their evolution laws and the interactions among different individuals are described. In the end, some social individuals occupy the monopoly position in their field.
When measuring the development status of individuals in social systems, it is often necessary to consider multiple dimensions. For the convenience of demonstration, in the simulative experiment, we
define three dimensions (that is, η=3) forλand ϕ, namelyX,YandZ. Moreover, due to the dynamic characteristics of the social system,the monopoly position in the current field will change over time,which is shown in the experiment as a dynamic change of ϕ.
What is more, a total of four different communication topologies are switched in order, and each topology is maintained for 2 s. Their adjacency matrices are used to describe the interactions among individuals in the social system. As the social system evolves, the social network will also change accordingly.
In our example, the number of agents in the field is set ton=12,the number of agents that finally occupy the monopoly position in the field is set tok=2, and the dimension of the development status of agents is set to η =3. Within the allowable range of hardware and calculation, inordertoachievefastconvergenceofthemodel, the remaining parameters areset tom=0.01,ℓ=1,δ=5, ϑ=105, and the execution time T =8 s. In the field of the example, the initial development status of the twelve agents (A1, A2, ..., A12) are randomly assigned, and then they continue to accumulate advantages under the influence of the Matthew effect, and finally two of them obtain monopoly status in this field. When the gap between an agent and the monopoly position is less than 0.01, the agent is considered to be in a monopoly position. The simulative results are shown in Fig. 2.
The structures of four communication topologies of the social network composed of twelve agents are shown in Fig. 2(a). In Fig. 2(b),the outputs of thek-WTA network converge to the correct value in a short time. Among them, the corresponding outputs of the two agents with cumulative advantages are 1, and the others are 0. The outputs of thek-WTA network undergo a change att=0.35 s, which means that the agents with cumulative advantages changed. In addition,Fig. 2(c) displays the gaps between each agent and the monopoly position. Figs. 2(d)−2(f) show the entire process of system evolution under the Matthew effect.
According to Fig. 2(d), it can be seen that, initially, the monopoly position in the field is around (7.7, 7.8, 0.3), which is marked with a red cross. The twelve agents are marked with circles of different colors, randomly distributed in society. Contact Fig. 2(b) to know that the two most advantageous agents at this time are A6 and A8.Their correspondingk-WTA network outputs are 1. Therefore, these two agents develop towards the monopoly position, and the gaps between them and the monopoly position are constantly narrowing.
The remaining ten agents are difficult to accumulate advantages to develop themselves, and can only grow or shrink with changes of the social environment (such as the promulgation of new policies, shortage of raw materials, and climate changes, etc.). With the evolution of the system, referring to Figs. 2(b) and 2(c), A2 (which is called the new winner) surpasses A8 (which is called the new loser) to become one of the two most dominant agents att=0.35 s and then develops rapidly with A6, while the development of A8 stagnates. Whent=6 s,A2 and A6 successfully occupy the monopoly position in this field.The overall trajectory of these simulative results is smooth with slight fluctuations. Additionally, the above simulative results prove the effectiveness of the proposed model (17).
Furthermore, the proposed social system evolution model under the Matthew effect can be applied in many fields. For example, in elections in the field of political science, candidates with greater current advantages are more likely to obtain more resources to strengthen themselves, thereby attracting more voters’ supports. In the field of economics, the ultimate manifestation of the WTA phenomenon is oligopoly, that is, only a few large and powerful companies control most of the market share. Besides, due to the existence of herd mentality, brands at the top of the rankings are more likely to be selected by consumers in brand marketing. These social phenomena all match the model proposed in this letter.
Conclusions:This letter has investigated the influence of the Matthew effect in the evolution of individuals in social systems under switching social networks. Thek-WTA competitive strategy has been utilized to control the evolution of agents in social systems under the Matthew effect, and the distributed consensus filter with compensation for switching communication topologies has been used to describe the interactions among individuals in social systems.Through theoretical analyses and simulative experiments, the effectiveness and availability of the proposed model have been verified. In future research, we will consider various influencing factors in social systems, such as development obstacles and time delay, so as to further enhance the flexibility and accuracy of the model.
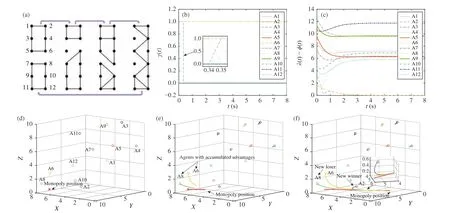
Fig. 2. Evolutionary process of the social system under the Matthew effect with n =12 and k =2. (a) Communication topology switching rule. (b) Outputs of k-WTA network. (c) Gaps between the individuals and the monopoly position. (d) Snapshots for agents and the corresponding evolutionary process at t=0 s.(e) Snapshots at t =0.29 s. (f) Entire evolutionary process of agents and the monopoly position.
Acknowledgments:This work was supported by the National Natural Science Foundation of China (62176109), the Natural Science Foundation of Gansu Province (21JR7RA531), the Tibetan Information Processing and Machine Translation Key Laboratory of Qinghai Province (2021-Z-003), the Youth Science and Technology Foundation of Gansu Province (20JR10RA639), and the Super-Computing Center of Lanzhou University.
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- An Overview and Experimental Study of Learning-Based Optimization Algorithms for the Vehicle Routing Problem
- Towards Long Lifetime Battery: AI-Based Manufacturing and Management
- Disagreement and Antagonism in Signed Networks: A Survey
- Finite-Time Distributed Identification for Nonlinear Interconnected Systems
- SwinFusion: Cross-domain Long-range Learning for General Image Fusion via Swin Transformer
- Real-Time Iterative Compensation Framework for Precision Mechatronic Motion Control Systems
