Self-Supervised Monocular Depth Estimation via Discrete Strategy and Uncertainty
2022-07-18ZhenyuLiJunjunJiangandXianmingLiu
Zhenyu Li, Junjun Jiang, and Xianming Liu
Dear Editor,
This letter is concerned with self-supervised monocular depth estimation. To estimate uncertainty simultaneously, we propose a simple yet effective strategy to learn the uncertainty for selfsupervised monocular depth estimation with the discrete strategy that explicitly associates the prediction and the uncertainty to train the networks. Furthermore, we propose the uncertainty-guided feature fusion module to fully utilize the uncertainty information. Codes will be available at https://github.com/zhyever/Monocular-Depth-Estimation-Toolbox.
Self-supervised monocular depth estimation methods turn into promising alternative trade-offs in both the training cost and the inference performance. However, compound losses that couple the depth and the pose lead to a dilemma of uncertainty calculation that is crucial for critical safety systems. To solve this issue, we propose a simple yet effective strategy to learn the uncertainty for selfsupervised monocular depth estimation using the discrete bins that explicitly associate the prediction and the uncertainty to train the networks. This strategy is more pluggable without any additional changes to self-supervised training losses and improves model performance. Secondly, to further exert the uncertainty information,we propose the uncertainty-guided feature fusion module to refine the depth estimation. The uncertainty maps serve as an attention source to guide the fusion of decoder features and skip-connection features. Experimental results on the KITTI and the Make3D dataset show that the proposed methods achieve satisfying results compared to the baseline methods.
Estimating depth plays an important role in the perception of the 3D real-world, and it is often pivotal to many other tasks such as autonomous driving, planning and assistive navigation [1]–[3]. Selfsupervised methods trained with many monocular videos have emerged as an alternative for the depth estimation [4]–[6] since the ground truth RGB-D data is costly. These methods treat the depth estimation as one of novel view-synthesis by training a network to predict target images from other viewpoints. In general, the framework consists of a depth network to predict image depth and a pose network to predict the camera ego-motion between successive image pairs, and aims to minimize the photometric reprojection loss in the training stage. Moreover, the smooth regularization [5], [6] and the masking strategy [4], [5], [7] are commonly included in the selfsupervised loss for sharper estimation results.
However, complex self-supervised training losses that couple the depth and the pose lead to a dilemma of uncertainty estimation [8],which is extremely vital in safety critical systems, allowing an agent to identify unknowns in an environment and reaches optimal decisions [6]. The popular log-likelihood maximization strategy proposed in [9] causes sub-optimal modeling and fails to beneficially work in the self-supervised situations [8]. This strategy needs to reweight all the loss terms during training stage to get reasonable uncertainty predictions, leading to a plight re-balancing the delicately designed loss terms in self-supervised depth estimation. In contrast,we aim for a pluggable uncertainty prediction strategy that can leave the weights of loss terms untouched.
In this paper, instead of pre-training a teacher network to decouple the depth and the pose in losses [8], which doubles the training time and the parameters, we aim to learn the uncertainty by a single model in an end-to-end fashion without any additional modifications to the self-supervised loss terms. To this end, we apply the discrete strategy[10]. Following [9], We train the network to infer the mean and variance of a Gaussian distribution, which can be treated as the prediction and the uncertainty, respectively. After that, we divide the continued interval into discrete bins and calculate the probability of each bin based on the mean and the variance. A weighted sum of the normalized probabilities is then served to calculate the expected prediction. Such a strategy can explicitly associate the prediction and the uncertainty before calculating losses. After self-supervised training withonly a simpleadditionalL1uncertainloss,ourmethod can masterthe capabilitytopredictthe uncertainty.Itis more pluggable for self-supervised methods and improves the model performance in addition. Furthermore, our method also guarantees the Gaussian probability distribution on the discrete bins, which yields more reasonable and sharper uncertainty results compared to the method of standard deviation proposed in [6].
Moreover, to make full use of the uncertainty information, based on the U-net multi-scale prediction backbone [5], we propose an uncertainty-guided feature fusion module to refine the depth estimation. Therefore, it will help the model pay closer attention to high-uncertain regions and refine the depth estimation more effectively. Sufficient experiments on the KITTI dataset [11] and the Make3D dataset [12] demonstrate the effectiveness and generalization of our proposed methods.
Our contributions are three-fold: 1) We propose a strategy to learn uncertainty for self-supervised monocular depth estimation utilizing the discrete bins. 2) We design an uncertainty-guided feature fusion module in the decoder to make full use of the uncertainty. 3)Extensive experiments on KITTI and Make3D dataset demonstrate the effectiveness of our proposed methods.
Methods:In this section, we present the importance of the main contributions of this paper: 1) A pluggable strategy to learn the depth uncertainty without additional modification to the self-supervised loss terms; and 2) An uncertainty-guided feature fusion module. We use the Monodepth2 [5] as our baseline. The framework with improvements is shown in Fig. 1.
Depth and uncertainty: Following [9], we simultaneously estimate the mean and the variance of the Gaussian distribution, which respectively represent the mean estimated depth and the measurement uncertainty. It is formulated by
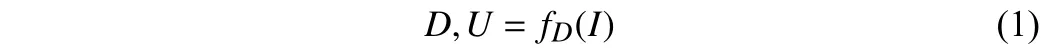
whereIis the input RGB image,Dis the mean estimated depth map,Uistheuncertainty map, andfDrepresents the depth estimation network.
In general, two key points are indicated in the design of loss terms tomakeuncertainty reasonable:1) AddingaL1losstoforcethe model topredict depthmore confidently; and2)Re-weightingthe loss terms according to the uncertainty. There will be a more relentless punishment for the pixel prediction results with a lower uncertainty. However, complex loss terms make 2) much more tough[9]. To this end, we combine the prediction and uncertainty before the loss computing.
To be specific, we divide the depth range into discrete bins,compute the approximate probability of each bin, and normalize the probabilities
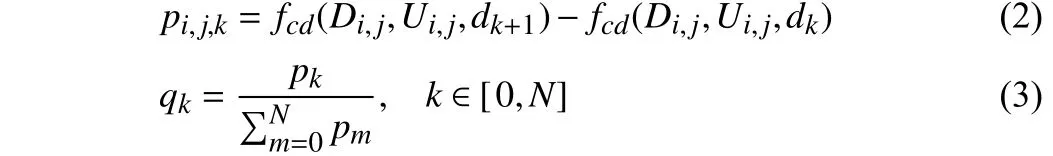

Fig. 1. Overview of our proposed methods. In part (a), the framework is based on Monodepth2 [5] that contains a U-net-based depth network and a pose network. We simply extend the depth network in Monodepth2 to estimate depth and uncertainty at the same time. (b) shows more details of the modified multiscale decoder. Successive uncertainty-guided feature fusion modules refine the depth estimation. Our strategy is performed at each output level to achieve multi-scale predictions. In (c), we illustrate details of the uncertainty-guided feature fusion module. It makes full use of the uncertainty information, containing two convolutions to extract useful information and an identity feature mapping to facilitate gradients back-propagation and preserve semantic cues.
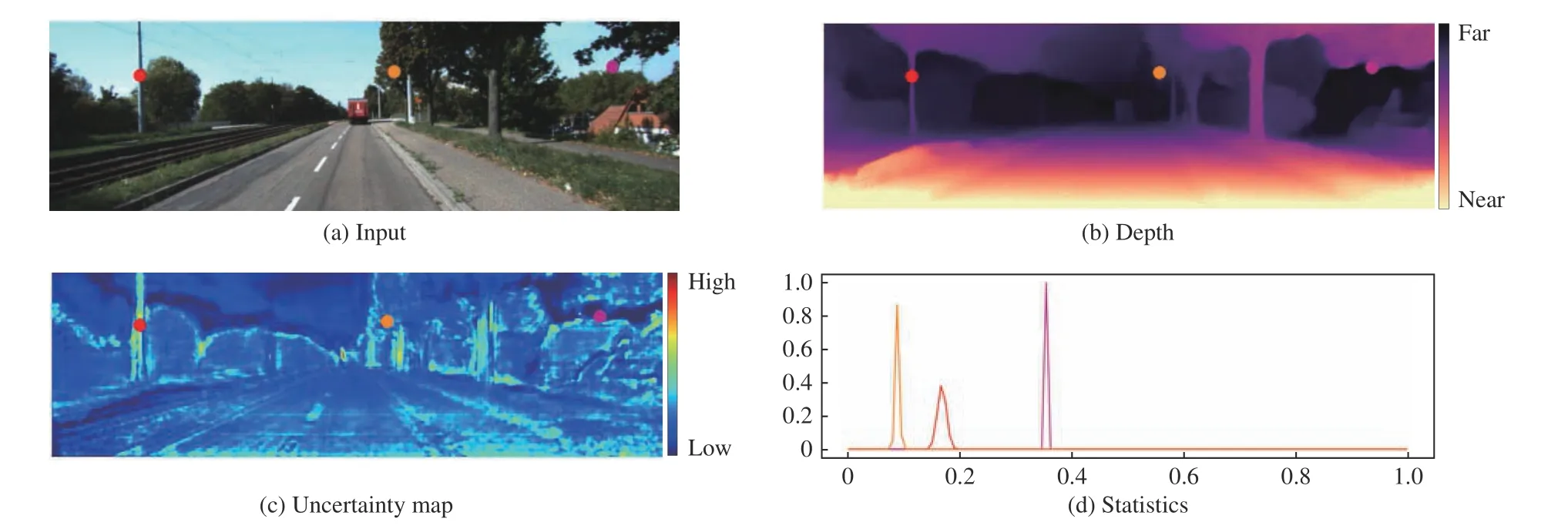
Fig. 2. Visualization Example. Given the input RGB (a), (b) and (c) show the depth and the uncertainty prediction, respectively. (d) shows the depth probability distributions for the three selected points in picture. Blue and orange points have sharp peaks, indicating low uncertainty. Red point has a flatter probability distribution which means high uncertainty.
whereiandjdenote the location of one pixel on the image. To make the representation more concise and cause no misunderstandings, we omit the subscriptsiandjin (2) and after.fcd(D,U,·) is the cumulative distribution function of the normal distribution whose mean and areDandU, respectively.dkis thek-th split point of the range,Nisthe number of bins, andqkis the probability after normalization.
Finally, we calculate the expected depth as following:
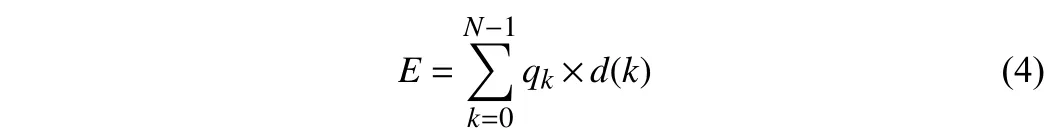
whered(k) represents the depth of thek-th bin andEis the expected depth. We use the expected depth to train our modals like other discrete bins based method [6].
Notably, the expected depth is not equal to the predicted mean depth thanks to the discrete strategy. Therefore, we combine the mean and the variance explicitly before the loss calculation. In the mathematics view, smaller variance leads to a relatively higher lower bound of the self-supervised losses. Models are forced to predict more precise depth at pixels with smaller variance, thereby predicting reasonable uncertainty. Such a strategy avoids complicating the selfsupervised losses.
In the training stage, we apply the minimum per-pixel photometric reprojection errorlp, the auto-masking strategy and the edge-aware smoothness losslsproposed in our baseline to train our model.Limited by pages, we recommend referring all the details in [5].
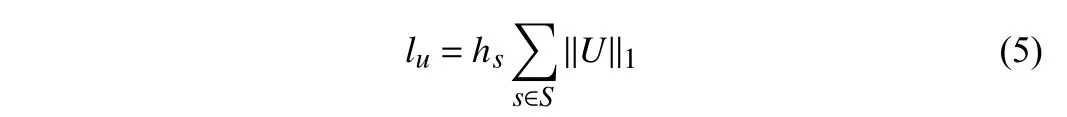
Additionally, we also want the model to provide more confident results with less uncertainty, so we add an uncertainty loss followinglu[9]:hsmeans the hyperparameter factors in multi-scale outputS={1,1/2,1/4,1/8}. The scale factorshsare set to 1 ,1/2,1/4,1/8 to force the model decrease uncertainty (i.e., increase the punishment on uncertainty) during the depth refinement process. The total loss can be written as
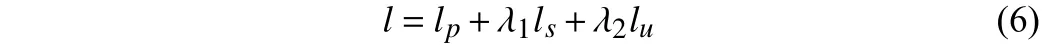
where λ1and λ2are the hyperparameters for weighing the importance of the smoothness loss and the proposed uncertainty loss.Both the pose model and depth model are trained jointly using this loss. Hyperparameter λ1follows the setting in origin paper [5].
Examples of the probabilities on bins are shown in Fig. 2. We can see a sharper peak at a low-uncertainty point (please refer to the blue and orange points), which means the model is more confident with the estimation. A higher-uncertainty point has a flatter probability distribution (the red point), indicating the model is uncertain about the prediction.
Fusion module: Uncertainty maps can provide the information of how confident the depth estimation is, which can help the depth refinement process to focus on areas with high uncertainty [13].
Therefore, we propose the uncertainty-guided feature fusion module to refine the depth estimation. The proposed uncertaintyguided feature fusion module contains three main components as shown in Fig. 1(c), which are two 3×3 convolution layers and an identity feature mapping. Specifically, the first concatenation and convolution layer is used to extract low-uncertain information and filter high-uncertain features to make the model pay closer attention to high-uncertainty areas. The output is then concatenated with the skip connected feature and the uncertainty map, and they are fed into the second convolution layer. This allows effective feature selection between feature maps. Finally, identity mapping is used to facilitate gradient back-propagation and preserve high-level semantic cues[14].
The fusion module,whichutilizesthepredicted uncertaintyUto fus e theupsampled featuresFuandthe skipconnectedfeaturesFs,ca n be formulated as

In the multi-scale depth decoder, the uncertainty-guided feature fusion module is repeatedly applied to the gradual feature fusion procedure to refine the depth estimation. It helps the model pay closer attention to higher-uncertain depth estimation areas and refine the depth estimation more effectively.
Experiments:
Datasets: We conduct a series of experiments on the KITTI dataset[11] and the Make3D dataset [12] to prove the effectiveness of the proposed methods. KITTI contains 39 810 monocular triplets for training and 4424 for validation. After training our models on the KITTI dataset, we evaluate them on the Make3D dataset without further fine-tuning.
Implementation details: We jointly train the pose and depth network by the Adam Optimizer with β1=0.9 and β2=0.999 for 25 epochs. The initial learning rate is set tolr=1E−4. We use a multilearning rate decay which drops tolr=1E−5 at after 15 epochs and decay tolr=1E−6 after 20 epochs. Following [6], we include a context module. By sufficient experiments, the weights in (6) are empirically set to λ1=1E−3 and λ2=1E−2, which can get the best results.
Evaluation metrics: For the quantitative evaluation, several typical metrics [15] are employed in our experiments
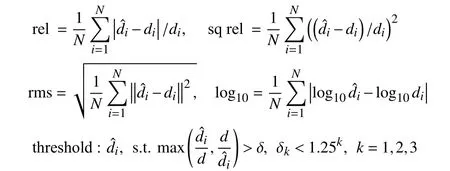
Performance comparison: We first evaluate our models on the KITTI dataset. The quantitative results compared with other methods are shown in Table 1. With the proposed methods, our models further decrease the evaluation error and achieve higher accuracy. We also provide some qualitative results in Fig. 3 . Our models provide sharper and more accurate results on object boundaries such as signboards, lamp posts, and background buildings. Furthermore,uncertainty maps also provide useful information. As shown in the first sub-figure in Fig. 3, the depth estimation of the closer round signboard is not very satisfactory with clear and accurate boundaries.On the uncertainty map, such inaccurate areas have higher uncertainty. Then, we compare the uncertainty maps with other methods. As shown in Fig. 4, the uncertainty maps we provided are more reasonable without artifacts from close to far and have more detailed information than the results in [6].
Ablation study: Table 1 also shows the quantitative results of the ablation study. As for low-resolution images (640×192), based on Monodepth2 (Baseline), we can observe the better per formation in almost all the evaluation measures by the discrete strategy (+ DS).Uncertainty-guided feature fusion module (+ UGF) also provides a satisfying improvement. The ablation study for high-resolution images (1024×320) also shows the effectiveness of our proposedmethods.
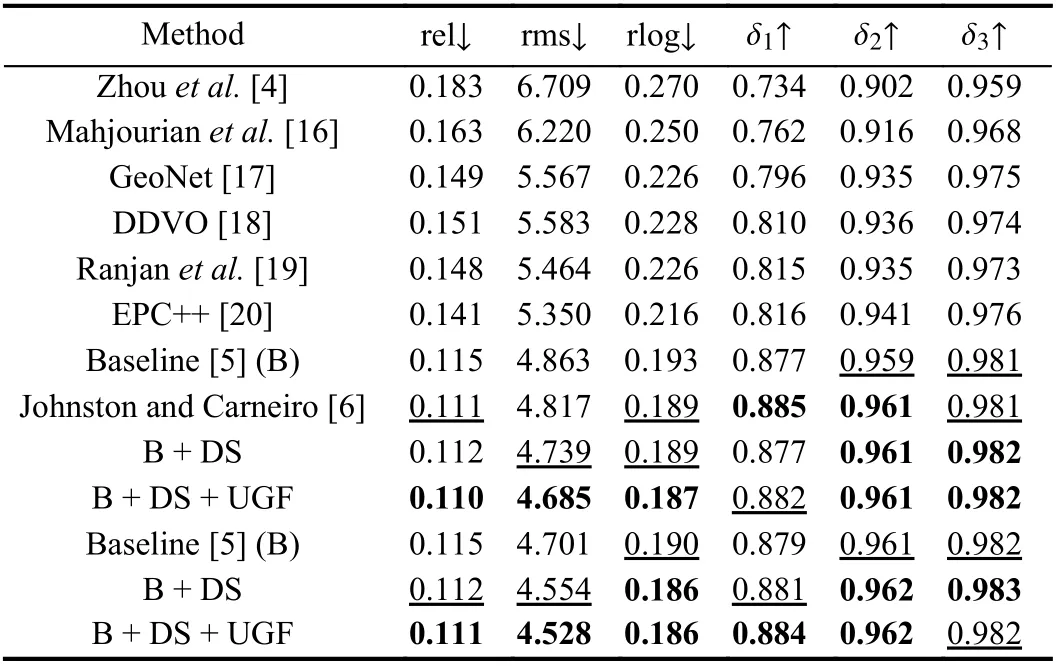
Table 1.Quantitative Results. Comparison of Existing Methods to Ours on the KITTI 2015 [11] Using the Eigen Split [15]. The Best and Second Best Results are Presented in Bold and Underline for Each Category. The Upper/Lower Part is the Low/High Resolution Result (640×192/1024×320). DS: Discrete Strategy. UGF: Uncertainty-Guided Fusion Module. DDVO: Differentiable Direct Visual Odometry

Fig. 3. Qualitative results on the KITTI Eigen split. Our model produce sharper depth maps than baseline MonoDepth2 (MO2), which are reflected in the superior quantitative results in Table 1. At the same time, uncertainty depth maps are provided for high-level applications.
We also provide some qualitative ablation study results in Fig. 4.Comparing the depth estimation results, the model with the uncertainty-guided feature fusion module provides sharper and more accurate results. Furthermore, there is a more prominent deep blue(lower uncertainty) area in uncertainty results provided by the model with an uncertainty-guided feature fusion module, which indicates the module can further reduce the uncertainty of depth estimations.
Generalization test: To further evaluate the generalization of our proposed methods, we tested our model without fine-tuning on the Make3D dataset. The quantitative comparison results are tabulated in Table 2. It shows that our proposed method outperforms the baseline method with a significant margin. Qualitative results can be seen in Fig. 5. Our method results in sharper and more accurate depth maps and reasonable uncertainty estimations.
Result analysis and future work: As we can see in the qualitative results, the highest uncertain areas locate at the object edges, which may be caused by the smooth loss that blurry the object edges since the lack of prior object information and occlusion. Therefore,designing a more effective smooth regularisation term, introducing objective edge information, and taking more effective masking strategies will help model training procedures and reduce uncertainty.Additionally, the smooth areas with less texture (high shadow and sky) show the lowest uncertainty. It indicates that photometric loss may not be helpful enough to train the model in this kind of area.While our model can precisely estimate the depth in these areas, it is essential to develop a more effective loss to supervise these areas better.
While we have achieved more reasonable uncertainty maps, when we concatenate the uncertainty maps along the time axis, we find there will be fluctuations in different areas of the image. They will hurt the algorithm’s robustness, especially for the systems that request smooth predictions in the temporal domain. In the future, we will try to associate filter methods or explore more temporal constraints to make the prediction more smooth and stable, and it is much more meaningful work.
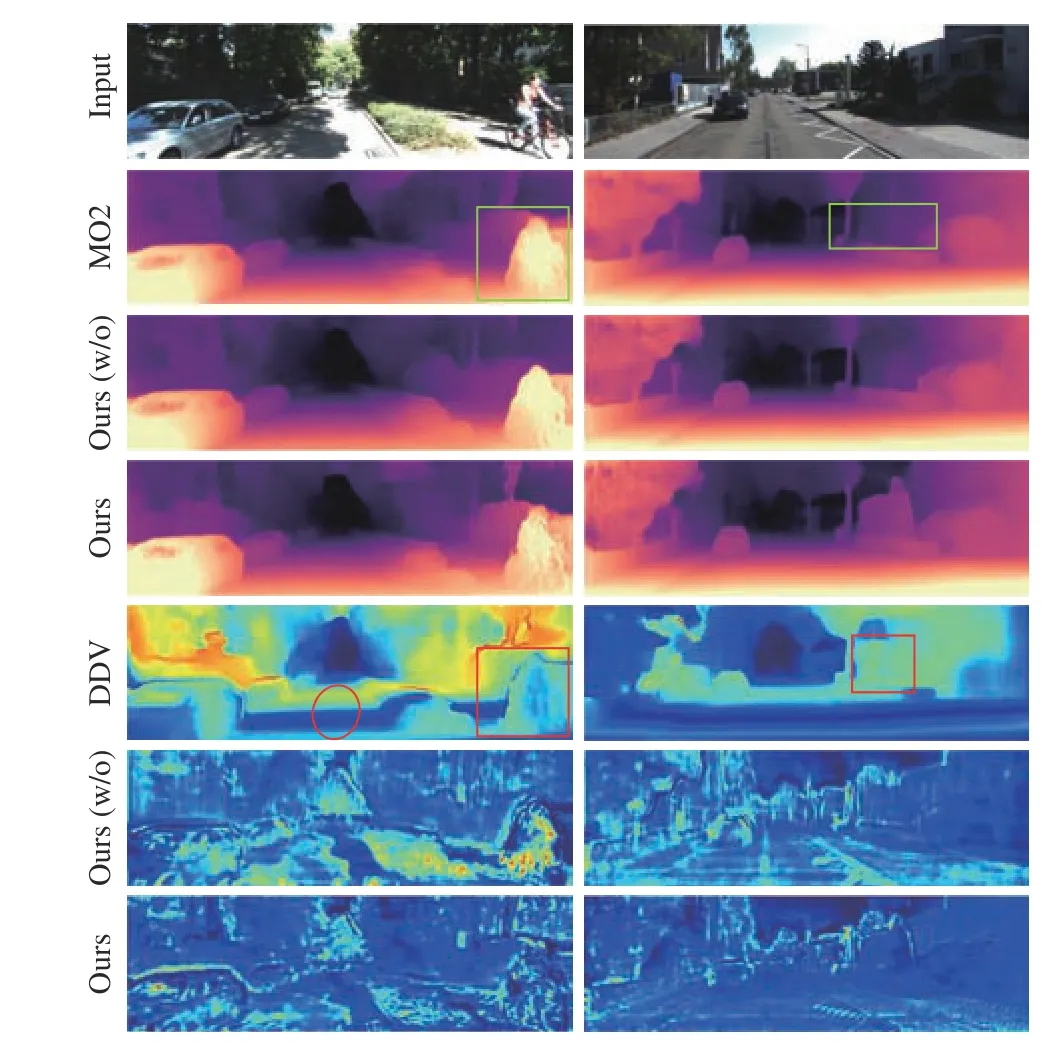
Fig. 4. Comparison examples. Ours (w/o) represents our method without the UGF. MO2 is the baseline. Discrete disparity volume (DDV) shows the uncertainty results from [6].
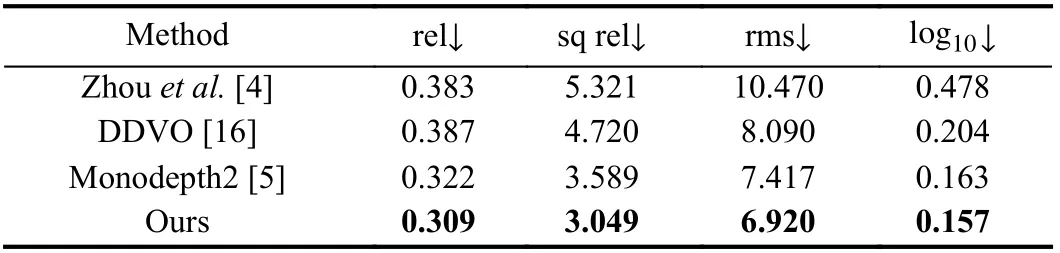
Table 2.Quantitative Results of the Make3D Dataset

Fig. 5. Qualitative results on the Make3D dataset. Our methods show a better effectiveness on the depth estimation and can also provide uncertainty maps.
Conclusion:This paper proposes a simple yet effective strategy to learn the uncertainty for self-supervised monocular depth estimation with the discrete strategy that explicitly associates the prediction and the uncertainty to train the networks. Furthermore, we propose the uncertainty-guided feature fusion module to fully utilize the uncertainty information. It helps the model pay closer attention to high-uncertain regions and refine the depth estimation more effectively. Sufficient experimental results on the KITTI dataset and the Make3D dataset indicate that the proposed algorithm achieves satisfying results compared to the baseline methods.
Acknowledgments:This work was supported by the National Natural Science Foundation of China (61971165), in part by the Fundamental Research Funds for the Central Universities (FRFCU 5710050119), the Natural Science Foundation of Heilongjiang Province (YQ2020F004).
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- An Overview and Experimental Study of Learning-Based Optimization Algorithms for the Vehicle Routing Problem
- Towards Long Lifetime Battery: AI-Based Manufacturing and Management
- Disagreement and Antagonism in Signed Networks: A Survey
- Finite-Time Distributed Identification for Nonlinear Interconnected Systems
- SwinFusion: Cross-domain Long-range Learning for General Image Fusion via Swin Transformer
- Real-Time Iterative Compensation Framework for Precision Mechatronic Motion Control Systems
