Two-Stage Robust Optimization Under Decision Dependent Uncertainty
2022-07-18YunfanZhangFengLiuYifanSuYueChenZhaojianWangandJoCatal
Yunfan Zhang, Feng Liu,,, Yifan Su, Yue Chen,,,Zhaojian Wang,,, and João P. S. Catalão,,
Abstract—In the conventional robust optimization (RO)context, the uncertainty is regarded as residing in a predetermined and fixed uncertainty set. In many applications, however,uncertainties are affected by decisions, making the current RO framework inapplicable. This paper investigates a class of twostage RO problems that involve decision-dependent uncertainties.We introduce a class of polyhedral uncertainty sets whose righthand-side vector has a dependency on the here-and-now decisions and seek to derive the exact optimal wait-and-see decisions for the second-stage problem. A novel iterative algorithm based on the Benders dual decomposition is proposed where advanced optimality cuts and feasibility cuts are designed to incorporate the uncertainty-decision coupling. The computational tractability,robust feasibility and optimality, and convergence performance of the proposed algorithm are guaranteed with theoretical proof.Four motivating application examples that feature the decisiondependent uncertainties are provided. Finally, the proposed solution methodology is verified by conducting case studies on the pre-disaster highway investment problem.
I. INTRODUCTION
A. Background
UNCERTAINTIES widely exist in real-world decisionmaking problems and various mathematical programming techniques, including scenario-based or chance-constrained stochastic programs, robust optimization (RO) [1] and distributionally robust optimization [2], have been developed to fit in different characteristics of the applications [3]. RO seeks a risk-averse solution by explicitly considering the worst-case effect of all possible realizations of the uncertain parameter within a pre-determined uncertainty set. It appeals especially when the decision maker has no knowledge of the probability distributions of the uncertain parameters, or when the feasibility of the system over the entire uncertainty set is prioritized. Due to its salient advantages on modeling capability, feasibility, and computational tractability [4], RO has gained increasing popularity over the recent decades and encompassed a wide variety of applications including process scheduling [4]–[6], power system planning and scheduling[7]–[10], and network optimization [3], [11], [12], etc.
In the context of RO, the uncertainty sets are usually assumed to be a priori and fixed. The underlying assumption is that the decision maker’s strategies would not alter the range of uncertainty realization. In many real-world decisionmaking problems, however, uncertainties can depend on the strategies chosen by the decision makers and are assumed as endogenous. For example, in a batch-process scheduling problem, the processing time or the production yield of a task is endogenously uncertain since it retains a physical meaning only when the optimizer decides to operate the associated task in a given period [4]–[6], [13]. Another example is the demand response program on buildings’ electricity consumption [8]. For buildings participating in the program, the reserve demand requested from the system operator is uncertain and of endogenous nature due to its dependency on the reserve capacity provided by the building in the day-ahead market. The uncertainties affected by decisions are called decision-dependent uncertainties (DDUs) or endogenous uncertainties. In this paper, we use these two terms interchangeably without distinction. Also, we refer to decisionindependent uncertainties (DIUs) or exogenous uncertainties as those not altered by decisions. Consideration of DDUs in RO problems can provide considerably less conservative solutions, attributed to the fact that DDUs can be proactively controlled by the optimizer. However, differently from DIUs,the presence of DDUs brings great challenges to solving RO problems, mainly due to the mutual influences between uncertainties and decisions. In this paper, we propose a convergence-guaranteed algorithm to efficiently solve the two-stage RO problems with DDUs.
B. Literature Review
Regarding RO under DDUs, existing works can be categorized into two classes, based on whether there are recourse or wait-and-see decisions after the revelation of uncertainty realization:
1)Static RO Under DDUs:In static RO, which is also called single-stage RO, all the decisions are here-and-now,i.e., to be determined before observing the uncertainty realization. In [14] and [15], variable budgeted static RO is studied, where the budget parameter that regulates the conservatism of the uncertainty set is modeled as an affine function with respect to the decision variables. In [16],polyhedral and conic uncertainty sets are introduced where decisions control the upper bounds of the uncertain variables.In [3] and [4], uncertainties are governed by binary-valued materialization indicator variables. The materialization indicator attains the values of 1 if the corresponding uncertain parameter retains a physical meaning in the problem and 0 otherwise. The DDU-involved RO models in the above works maintain the advantage of computational tractability of conventional RO problems, since a robust counterpart of mixed-integer linear programming (MILP) formulation can be derived by applying the strong duality theory and McCormick envelopes convex relaxation.
2)Adaptive RO Under DDUs:Adaptive robust optimization(ARO), or called adjustable RO [17], is established in a twostage or a more general multi-stage setting where recourse or wait-and-see decisions are incorporated in response to actual uncertainty realization. The computational complexity of ARO lies in the fact that multi-level programming problems with more than two decision levels are non-deterministic polynomial-time (NP)-hard [18]. To overcome this intrinsic computational burden as well as the challenges raised by the coupling relationship between the here-and-now decisions and the uncertainties, affine decision rules parameterized in the uncertainty realizations and the here-and-now decisions are postulated on the wait-and-see decisions in [5], [19]–[21].Differently from the aforementioned approximate affine policies, the decision rules in [22] are generated with the aid of multi-parametric programming technique, rendering the exact solution to the ARO problem; however, computation burden of solving the second-stage problem parametrically as an explicit function of the here-and-now decisions and the uncertainty is transferred off-line but not eliminated. In the line of primal cut algorithms [23], [24], [9] proposes an improved column-and-constraint generation (C&CG) algorithm based on a worst-case scenario mapping technique. Its application, however, is limited to a high-dimensional rectangle decision-dependent uncertainty set (DDUS).
Compared with conventional ARO problems, the challenges of solving DDUs-incorporated ARO problems reside in the fact that the existing cutting plane algorithms [23]–[26], with constraints generated by whether primal or dual information of the second-stage problem, fail to warrant finite convergence to the global optimum when the uncertainty set depends on the here-and-now decision variable which changes with iterations. This is because in that case the optimality cuts and feasibility cuts generated with concrete uncertain parameter values may become invalid and ruin the optimality of the solution, or even render an infeasible master problem which falsely implies that the original ARO problem is not robust feasible. Moreover, since the vertices of the uncertainty set change with the here-and-now decision, it is difficult to justify the finite convergence of these cutting plane algorithms by completely enumerating the vertices of the polyhedral uncertainty set. To the best of the authors’ knowledge, the solution approach for ARO under DDUs with a generic decision-dependency and without any assumption on approximation policies has not been addressed.
C. Contribution and Organization
The main contributions of this paper are twofold:
1)From a Modeling Perspective:This paper addresses a generic two-stage robust optimization model with a class of polyhedral DDUSs whose right-hand-side vector has a dependency on the here-and-now decisions. Differently from[3], [4], [6], [14]–[16] that contemplate the static RO involving endogenous uncertainty, our two-stage RO grants more feasibility by the implementation of wait-and-see decisions after the revelation of uncertainty realization.Compared with [5], [20], [21] that are established in a twostage or multi-stage setting and postulate affine decision rules on the wait-and-see decisions, our model seeks to derive the exact optimal solution to the second-stage problem. In view of the DDUS, we extend the polyhedral uncertainty sets with reduced decision-dependency considered in [6], [8], [9], [15],[16] into a generic form where both the shape and size of the uncertainty set may be altered by decisions. Due to the aforementioned improved modeling capability, our model can considerably eradicate the conservatism effects of RO by proactively controlling the level of uncertainties and inherently capture the trade-off between the robustness and conservatism of the solution.
2)From a Solution Standpoint:To solve the two-stage RO model with DDUs, we propose a novel iterative solution algorithm involving one master problem and two subproblems, based on the Benders dual decomposition.Compared with the C&CG algorithm [23], [24] which is widely applied to conventional two-stage RO problems, the proposed algorithm overcomes the challenges stemming from endogenous worst-case uncertainty scenarios by using only dual information of the second-stage problem. Also differently from classical Benders dual cutting-plane algorithms[25]–[27], advanced optimality cuts and feasibility cuts are designed to accommodate the coupling between uncertain parameters and decision variables. Performance of the proposed algorithm, including convergence and optimality, is guaranteed with a strict proof. To implement the algorithm,we derive the robust counterpart of the master problem and the reformulations of the sub-problems, maintaining the computational tractability of the proposed solution algorithm.
The remainder of the paper is organized as follows. The remainder of this section introduces the notation. The mathematical formulation of the two-stage RO with DDUs is provided in Section II. Section III proposes the solution approach based on modified Benders decomposition. Section IV addresses some implementation issues of the proposed algorithm, including the derivation of a tractable robust counterpart of the master problem which is a static RO and the reformulation of the bi-level sub-problems into MILPs. In Section V, four examples are provided as the applications of the proposed model and solution methodology. And we present a case study on the pre-disaster highway network investment problem. We conclude the paper in Section VI.
Notation:Rnis the set ofn-dimensional real vectors and Rm×nis the set ofm×nreal matrices. Z ( Z+) denotes the set of(positive) integers. [n]≜{1,...,n} denotes the set of integers from 1 tonand [0]≜∅.Fora vectorx∈Rn(amatrixA∈Rm×n),xT(AT)denotes its transpose. Weuse1and0 to denote vectors of ones and zeros, respectively. Forx,y∈Rn,we denote theinnerproductxTy=xiyiwherexi,yistand for thei-th entries ofxandy, respectively. The Hadamard product is defined asx◦y=(x1y1,...,xnyn)T, i.e., the elementwise product of two equally-sized vectors or matrices. For a polytopeX⊆Rn, vert(X) is the set of the vertices ofX. ⎿a」 is the largest integer less than or equal toa. We define the difference of setXandYasXY≜{x:x∈X,x∉Y}.
II. PROBLEM FORMULATION
A. Two-Stage RO With DDU
The two-stage RO with DDU (TRO-DDU) problem is formulated as
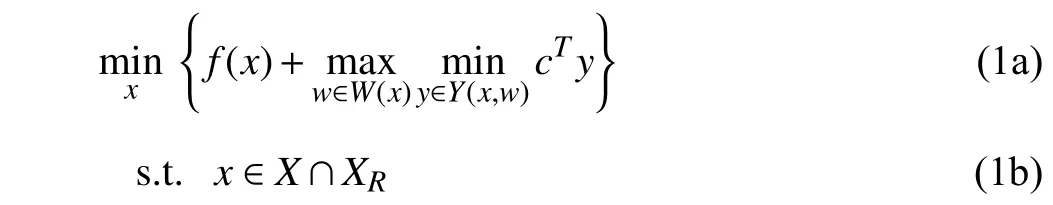
where
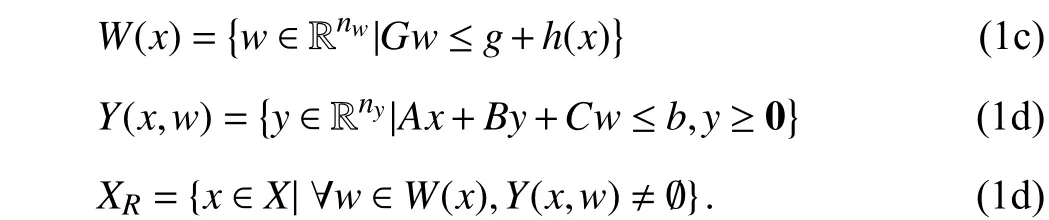
The here-and-now decisionx∈RnR×ZnZ is a mixed-integer variablevectorwitha dimensionofnx=nR+nZ.X⊆RnR×ZnZis the feasibleregionofx.f(x):RnR×ZnZ →R1is the costfunction withrespecttox.TheDDU parameteris denoted byw∈Rnwand the DDUSofwisW(x):RnR×ZnZ2Rnw,which is essentially a set-valued map parameterized byxwhereG∈Rr×nwis a constant matrix,g∈Rris a constant vector andh(x):RnR×ZnZ →Rris a vector-valued function with respect tox. The wait-and-see decision vector isy∈Rny.We consider the case that the second-stage decision problem isalinearprogram(LP) andc∈Rnydenotesthecost coefficientofy.Y(x,w):RnR×ZnZ×Rnw2Rny,whichis essentially a set-valued map parameterized byxandw,denotes the feasible region ofywith a specific form in (1d)whereA∈Rm×nx,B∈Rm×ny,C∈Rm×nwandb∈Rmare constant parameters. The constraint setXR⊆RnR×ZnZ defined in (1e) is the set ofxthat are robust feasible. A hereand-now decisionxis called robust feasible [1], [26] if for any realization of the uncertainwwithinW(x) there exists at least one feasible wait-and-see decisionylying withinY(x,w). The TRO-DDU problem (1) aims at minimizing the total cost of the two stages, which isf(x)+cTy, under the worst-case uncertainty realization. The following assumptions are made on problem (1).
Assumption 1:1)f(x) is a convex function; 2)Xis a convex set; 3)X∩XR≠∅; 4)Xis bounded,W(x) is bounded for anyx∈XandY(x,w) is bounded for anyx∈Xandw∈W(x).
Under Assumption 1-1) and 1-2), the nominal problem of(1) is a convex minimization problem. Assumption 1-3) and 1-4) imply that the TRO-DDU problem (1) is feasible and bounded, thus there exists the optimal solution to (1).
The TRO-DDU problem distinguishes itself from the existing literature by the consideration of the DDUwand the DDUSW(x). Regarding the generality of the DDU modeling in the TRO-DDU problem (1), we have the following remark.
Remark 1(Decision-Dependent Uncertainty Set):The polyhedral DDUSW(x) in (1c), whose right-hand-side vector has a dependency onx, covers the formulations proposed in the existing literature [8], [9], [14]–[16], [20], [21]. It provides generic modeling capability since both the shape and size of the uncertainty set can be altered byx. Moreover,W(x) in (1c)applies readily with DIUs by settingh(x)=0. Though the coefficient matrixGis fixed in (1c), the solution strategy proposed in Sections III and IV can be easily extended to the cases in [3]–[5] wherexaffects the coefficient matrix through certain binary-valued functions with respect tox.
Regarding the difficulty in solving TRO-DDU problem (1),we have the following remark.
Remark 2:The well-known C&CG algorithm is no longer applicable to TRO-DDU problem (1) since finite convergence to the global optimum is not warranted in the presence of DDUs.
1)Failure in Robust Feasibility and Optimality:The cutting planes in the C&CG algorithm with recourse decision variables in the primal space are generated with concrete values of the uncertain parameter for each identified scenario;and these cuts can become invalid when the uncertainty set depends on the here-and-now decisionxwhich varies with iterations. Forexample,given ahere-and-now decisionx1,the identified worst-case uncertaintyrealizationw1∈W(x1)would nevercometrueifanotherhere-and-nowdecisionx2is adopted andw1∉W(x2);andinthat case, thefeasibilityand optimality cuts generated according tow1no longer necessarily perform a relaxation to problem (1) and may ruin the optimality of the solution, or even render an infeasible master problem.
2)Failure in Finite Convergence:The finite convergence of C&CG algorithm is justified by a complete enumeration of the vertices of the uncertainty set. However, in problem (1), the vertices set of polytopeW(x) changes withxwhich varies with iterations, thus the C&CG algorithm no longer necessarily terminates within a finite number of iterations.
III. SOLUTION METHOD
A. Equivalent Transformation
1)Robust Optimality:Looking at the inner-level problem in
(1), we denote the following max-min bi-level optimization byS(x):
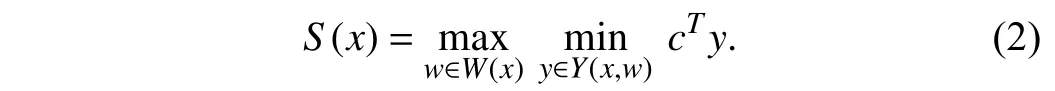
By noting the duality of the inner problem inS(x),S(x) can be equivalently transformed into the following bi-linear maximization problem:
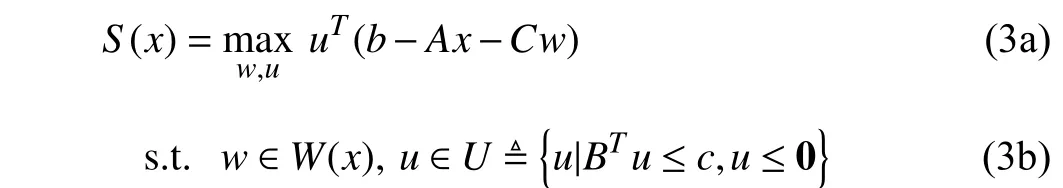
whereu∈Rmis the dual variable that corresponds with the constraintsAx+By+Cw≤b. Then, problem (1) is equivalent to
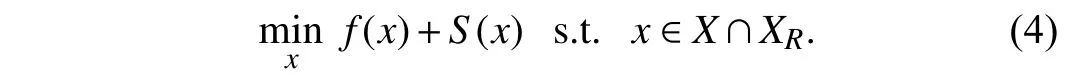
Introducing a supplementary variable α ∈R1, then problem(4) can be further rewritten in an epigraph form as
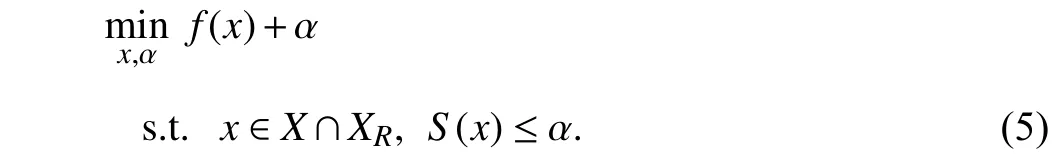
2)Robust Feasibility:The robust feasibility of decisionx,i.e., whetherxlies inXR, can be examined by solving the following relaxed bi-level problem:
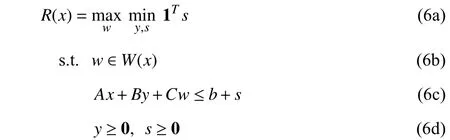
wheres∈Rmis the slack variable vector introduced to relax the feasible region ofydefined in (1d). IfR(x)≤0,xis robust feasible, i.e.,x∈XR.ElseifR(x)>0, theremustexista realizationw∗∈W(x)suchthat nofeasiblewait-and-see decisionyis available. It is useful to write the dual of the inner minimization problem inR(x) . ThenR(x) is equivalent to the single-level bi-linear optimization problem as follows:
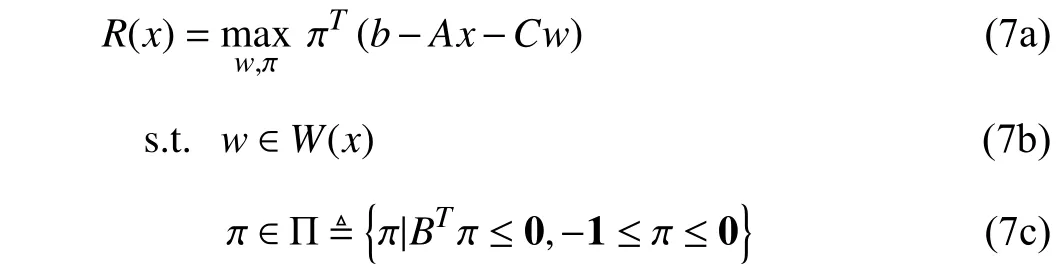
where π ∈Rmis the dual variable vector corresponding with constraints (6c). Sincex∈XRif and only ifR(x)≤0, problem(5) can be further written as
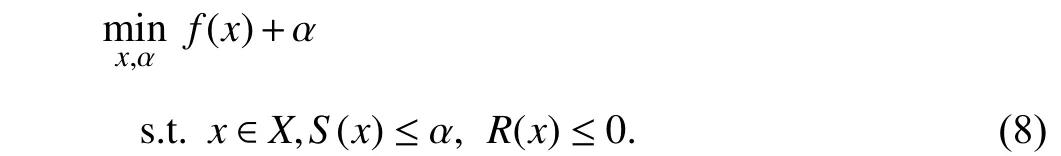
From the above transformation, we derive problem (8)which is the surrogate model of TRO-DDU problem (1).
B. Modified Benders Decomposition Algorithm
Next, we have the overall Algorithm 1 to solve problem (8)where the master problem (MP) involved is formulated as
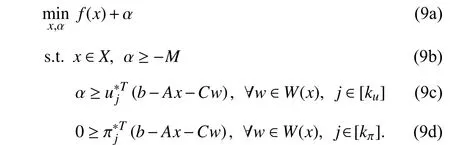
Regarding the difference between the proposed modified Benders dual decomposition (Algorithm 1) and the existing algorithms such as the C&CG algorithm and classic Benders dual cutting-plane algorithms, we give a remark as below.
Algorithm 1 Modified Benders Dual Decomposition Algorithm for TRO-DDU Problem (1)

Remark 3(Advanced Optimality and Feasibility Cuts):Constraints (9c) and (9d), which are appended to the master problem with iterations, are called optimality cuts and feasibility cuts, respectively. They are designed to have the following salient features to adapt to the DDUS: 1) Concrete worst-case uncertainty, i.e., the solution toR(xk) orS(xk)denoted bywk, is not involved in the optimality cuts or the feasibility cuts. This is different from the C&CG algorithm, as it incorporates the coupling relationship betweenxandw;2) Dual information of sub-problemsR(xk) andS(xk), i.e.,πkanduk, are utilized to generate the feasibility cuts and optimality cuts, inspired by the Benders dual decomposition.However, these cuts are designed to be no longer hyperplanes,but a set of static robust constraints, to comprise a cluster of endogenous worst-case uncertainty realizations.
Regarding the extensive adaptability of Algorithm 1, we have the following remark.
Remark 4(Adaptability to DDU Formulations):Algorithm 1 is designed to be applicable to a wide range of DDU formulations. Note that the explicit formulation of DDUSW(x)is not involved in Algorithm 1, nor in the theoretical justification of its performance. Thus, Algorithm 1 does not preclude the implementation of more DDUS structures besides polyhedrons, such as ellipsoidal and conic sets.However, considering the difficulty in solving master problem(9) and sub-problemsR(x) andS(x), here we focus on a class of polyhedral uncertainty sets with decision dependency in the right-hand-side vector, as formulated in (1c).
We justify the convergence and optimality of Algorithm 1 by the following theorem.
Theorem 1:Letqbe the number of vertices ofUdefined in(3b) andpbe the number of vertices of Π defined in (7c). Letx∗denote the optimal solution to the TRO-DDU problem (1).Then, Algorithm1terminateswithinO(p+q)iterationsand outputsthe solutionxksuch thatxk∈X∩XRand|f(xk)+S(xk)−f(x∗)−S(x∗)|<ε.
Theorem 1 indicates that the proposed modified Benders dual decomposition algorithm is finitely convergent to the optimum. Proof of Theorem 1 can be found in Appendix.
IV. ROBUST COUNTERPART AND BIG-M REFORMULATION
In this section, we show that the implementation of Algorithm 1 is computationally tractable, by deriving the robust counterpart of the master problem (9) and reformulations of sub-problemsR(xk) andS(xk).
In Algorithm 1, the master problem (9) involves static robust constraints (9c) and (9d). Without loss of generality,we illustrate how to deal with the robust constraint (9c) in the master problem by substituting it with its robust counterpart.
The following robust constraint with respect to (α,x) with given:
A. Robust Counterpart of the Master Problem
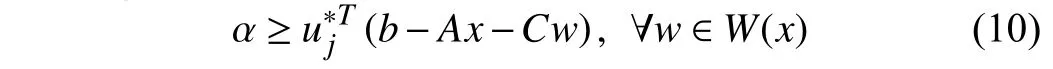
is equivalent to
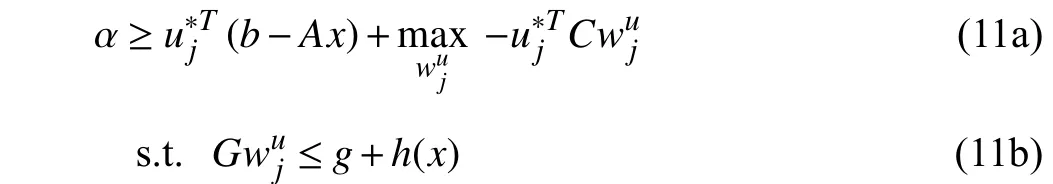
wherewesubstitutewbyfordenotingvariablein constraintformed by.Next,thefollowing twocasesare discussed:
1)A Bi-Linear TermλTh(x)can be Precisely Linearized Through the Big-M Method Whereλ ∈Rris an r-Dimensional Variable and x is annx-Dimensional Variable:To illustrate this, we takex∈{0,1}nxandh(x)=Hxas an example. Duality of the inner-level problem in (11) is deployed, thus (11) can be reformulated as
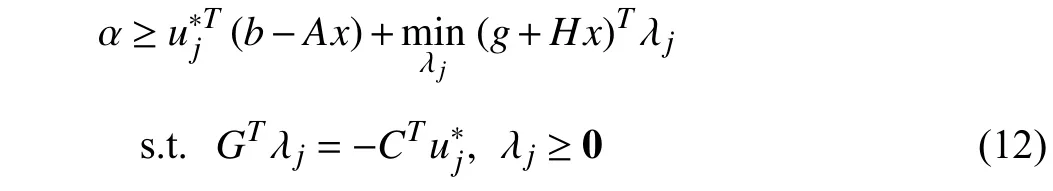
where λj∈Rris the dual variable corresponding with constraint (11b). Note that constraint (12) is equivalent to
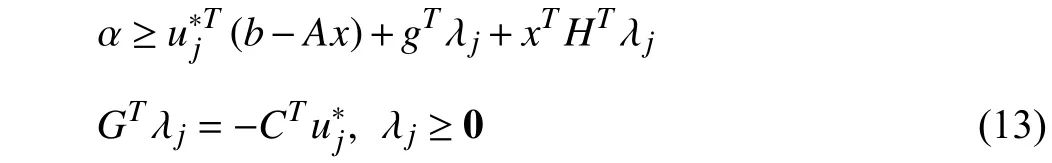
bydroppingthe minimizationoperation.Sincexisbinary,the bi-lineartermxT HTλjcanbeexactlylinearizedthroughthe big-Mmethodby introducingsupplementaryvariableηj∈Rnxand a largeenoughpositivenumberM,whereηj=x◦(HTλj).Then, constraint (13) has the following equivalent formulation:
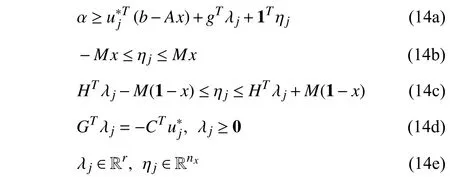
which constitutes the robust counterpart of constraint (10).The robust counterpart of feasibility cuts (9d) can be derived in a similar way. Thus the master problem (9) has the following MILP robust counterpart:
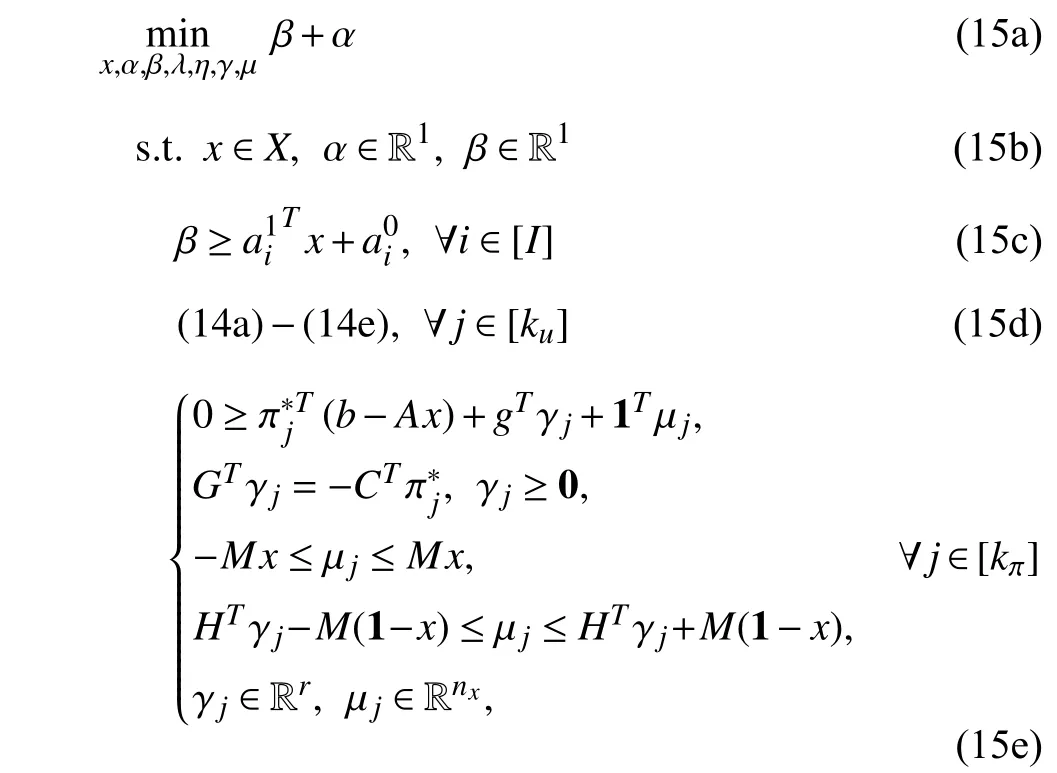
where the convex functionf(x) is substituted by its piecewise linearization form as in (15c) and the optimality cuts and the feasibility cuts are substituted by their robust counterparts.∈Rnx,∈R1(i∈[I])areconstant parameters for the piecewise linearizationoff(x).
2)Otherwise:If a bi-linear term λTh(x) cannot be exactly linearized by the big-M method, we deploy the Karush-Kuhn-Tucker (KKT) conditions of the inner-level problem in (11) as follows:
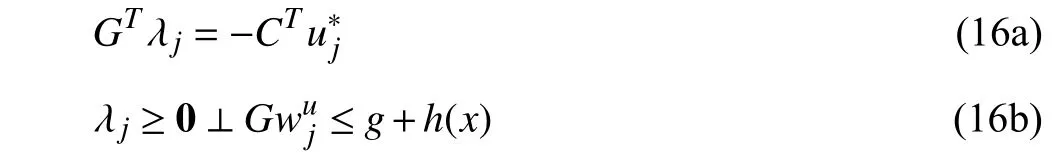
where λj∈Rris the dual variable corresponding with constraints (11b), and (16b) denotes the complementary relaxation condition. The nonlinearity of complementary condition (16b) can be eliminated through the big-M method by introducing the binary supplementary variablezj∈{0,1}r.Thus, the optimality cut (11) has the following equivalent robust counterpart:
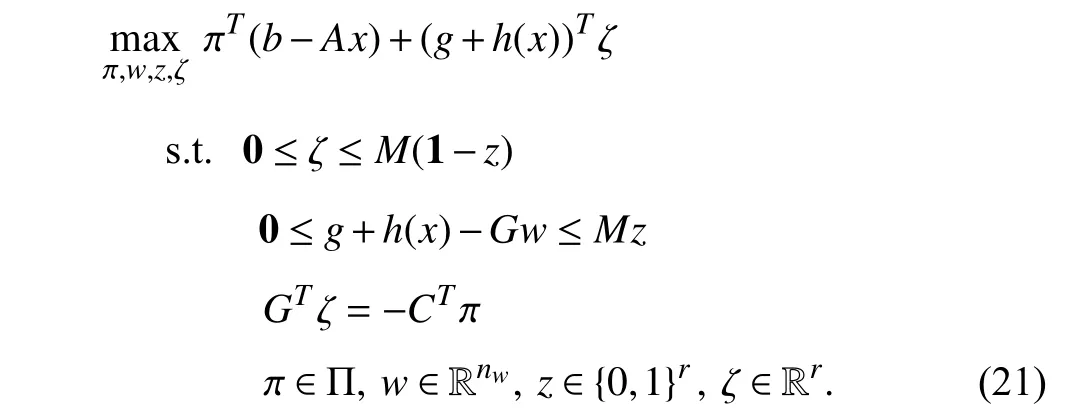
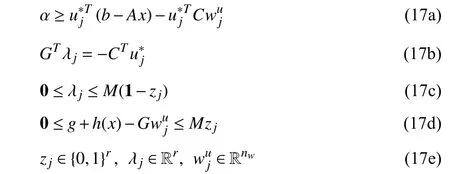
where the complementary relaxation condition (16b) is substituted by (17c) and (17d). The robust counterpart of the feasibility cut (9d) can be derived similarly. Thus the master problem (9) has the following robust counterpart which is a mixed-integer programming problem.
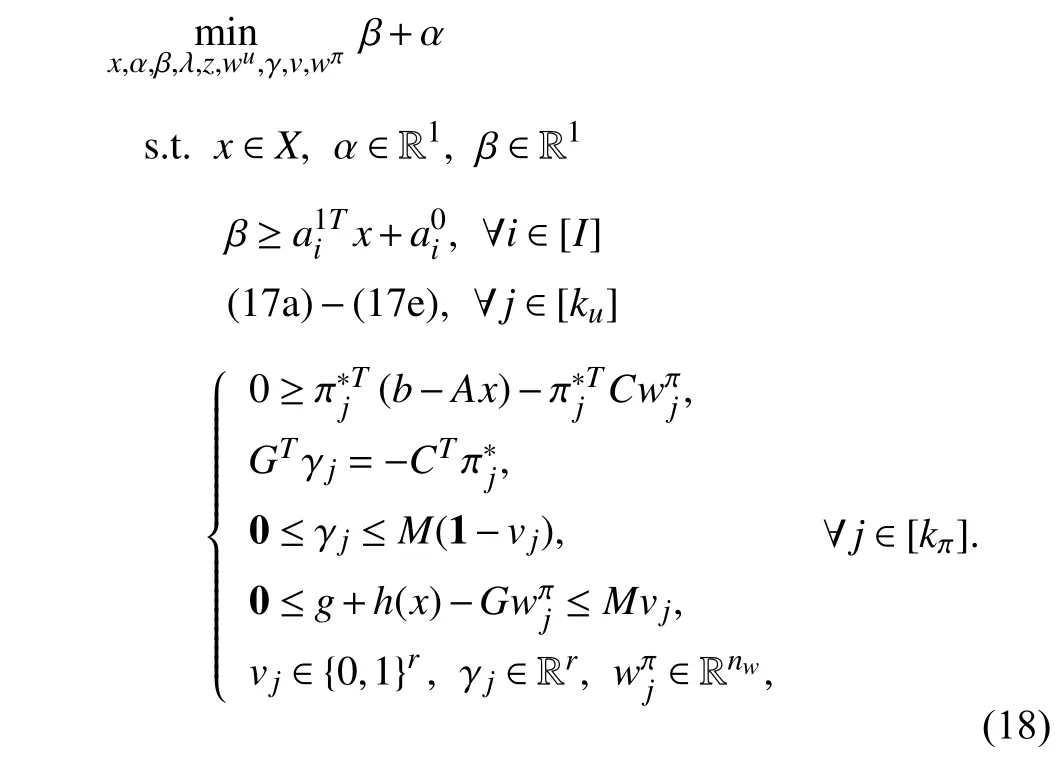
B. Reformulation of Sub-Problems
In Algorithm 1, the robust feasibility examination subproblemR(x) in (7) and the robust optimality sub-problemS(x)in (3) both have bi-linear objective, imposing difficulties on the solving. Next, we provide linear surrogate formulations ofS(x) andR(x). Since they have similar structure, without loss of generality we only focus onR(x).
R(x) in (7) can be equivalently rewritten into
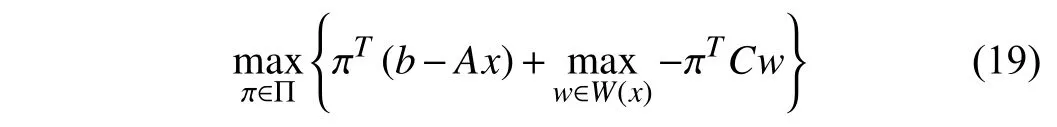
where the here-and-now decisionxis given by solving the master problem. We deploy the KKT condition of the innerlevel LP problem in (19) as follows:

where ζ ∈Rris the dual variable corresponding with constraintw∈W(x) in (19). The complementary constraints(20a) can be linearlized by introducing binary supplementary variablez∈{0,1}r. Then, the complementary constraints (20a)can be substituted with its equivalent linear formulations, like what we have done to (16b). Moreover, since strong duality holds, we substitute the − πTCwin (19) by (g+h(x))Tζ. Then,sub-problemR(x) is equivalent to the following MILP problem:
V. APPLICATIONS
The proposed model and solution algorithm cater for a variety of application problems. In this section, we provide four motivating DDU-featured examples that can be formulated into the proposed TRO-DDU model (1). For the first three applications, we focus on the endogeneity of the uncertainties by constructing the DDUS and do not go into the details of problem formulation. For the last application, predisaster network investment, detailed problem statements and numerical case studies are provided with an out-of-sample analysis.
A. Application 1: Batch Scheduling Problem
This case is from [13] (Section 8) where stochastic programming formulations with endogenous uncertainties are established. Here we reform the characterization of DDUs to fall in the scope of RO. Consider a chemical process network as shown in Fig. 1.
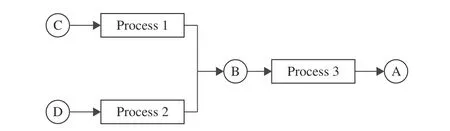
Fig. 1. Illustration of Application 1.
Here, chemical A is produced in Process 3 from chemical B while chemical B can be produced in Process 2 from chemical D or produced in Process 1 from chemical C. If needed,chemicals A, B, C, and D can be purchased from market. Now there is a demand for chemical A that must be satisfied and decisions on which specific processes should be operated are made to maximize the net profit. The per unit yields of the three processes, denoted by θi,tfor each processi∈I={1,2,3} and timet∈T, are uncertain. The endogeneity stems from the fact that θi,tretains a physical meaning only when processiis operated at time periodt. Letxi,t∈{0,1}denote the binary decision of operating processiat timet,then the DDUS forθis constructed as
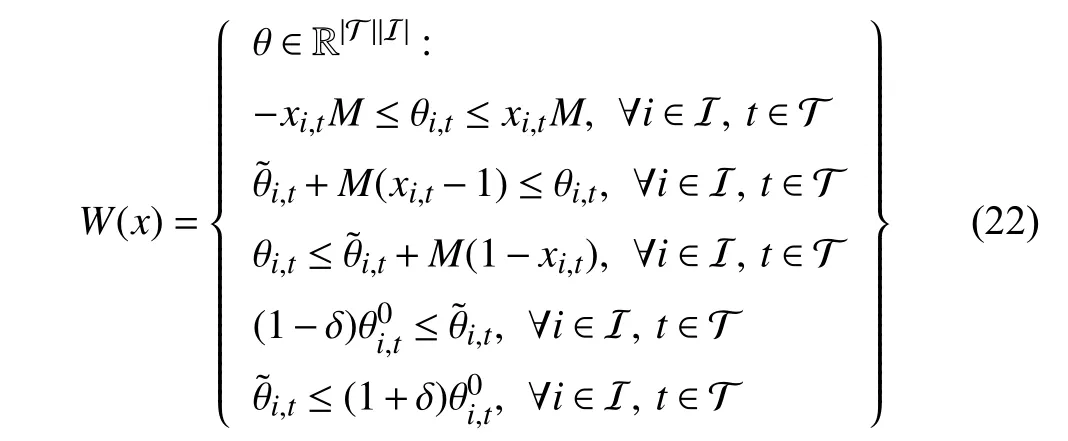
B. Application 2: Shortest Path Over an Uncertain Network
The second case comes from [16] (Example 2), considering to find the shortest path from the origin node A to the destination node B over a network with uncertain arc lengths,as shown in Fig. 2.
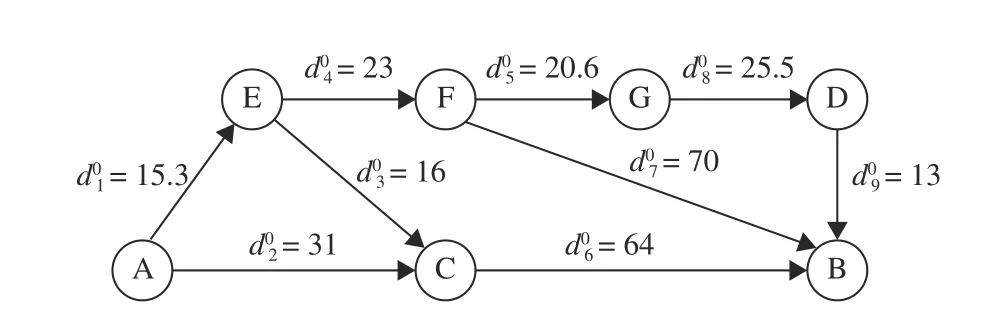
Fig. 2. Illustration of Application 2.
Let E denote the arcset of the graph and the uncertain length for an arce∈E is denoted byde. The uncertain arc lengthsdlie in the DDUS as follows:
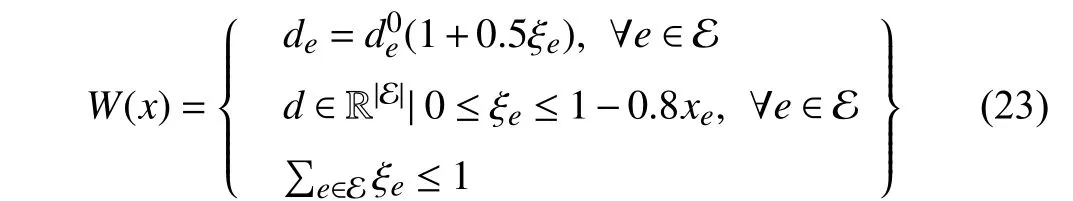
C. Application 3: Frequency Reserve Provision
The third application comes from [8]. Consider a smart building participating in the demand response program on electricity consumption. The building is asked by the grid operator to adjust its electricity consumption within a prespecified reserve capacity. The building is rewarded for providing this reserve service and the payment depends on both the size of the reserve capacity and the actually deployed reserve energy.
Consider a symmetric reserve capacityRt(Xt)=[−Xt,Xt]whereXt≥0 is the size of reserve capacity at timet. For the smart building, the operator’s real-time reserve deployment requestrtis endogenously uncertain at the planning stage. The endogeneity stems from the fact that the range of reserve deployment that the smart building admits is fundamentally affected by its decisions on the reserve capacity. Specifically,rt∈Rt(Xt) andXtis the building’s day-ahead decision. It is assumed that providing reserve capacity of sizeXtis rewarded byXtandofferingreserveenergyofsizertis compensatedbyrt.Thefrequencyreserveprovision problem is formulated to maximize the building’s profit while always satisfying inner technical and comfort constraints.
D. Application 4: Pre-Disaster Network Investment
In this subsection, a pre-disaster highway network investment problem is provided, including its problem formulation and a case study. This application is motivated by the work of [28] where the decision maker aims to strengthen the highway system in advance to prevent link failures due to earthquakes. By contrast, we model the problem into a twostage RO with DDUs for the case that link failure probabilities are not known.
The goal is to guarantee the existence of a path between a given origin-destination (O-D) pair after the earthquake and concurrently minimize the post-disaster travel cost from the origin node to the destination node and the costs of necessary pre-disaster investment. Endogenous uncertainties arise from the fact that the post-disaster state of each link, either functional or non-functional, is uncertain but can be altered by pre-disaster reinforcement.
1)Problem Formulation:The high-way network is modeled into a directed graphN=(V,E) with node setVand arc setE.To characterize the functionality of the highway system after the disaster, two nodes in the graphNare specified:Ddenotes the destination node which is the district with the highest expected damage in the earthquake, andOdenotes the origin node which usually refers to the district with the most support resources.
We use binary-valued variablexe∈{0,1}1to denote the investment decision on linke∈E.xetakes the values of 1 if thereisaninvestmentonlinkeand0otherwise.Letwe∈{0,1}1denotethedecision-dependentuncertainpostdisaster state of linke∈E.weattains the value of 1 if the linkeis not functional after the occurrence of the disaster and the value of 0 otherwise. Strengthened links have guaranteed functionality after the disaster and the non-strengthened links are subject to random failures. Thus the realization ofweis restricted by
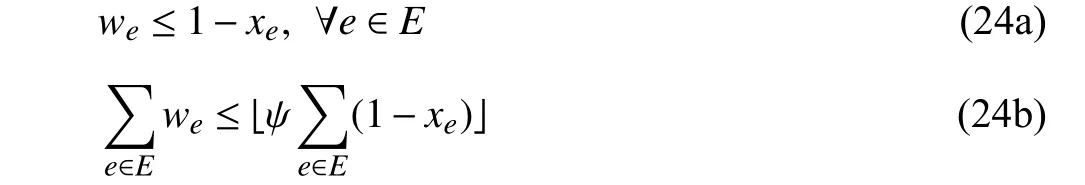
where ψ ∈[0,1] is the robustness budget to reduce conservativeness. Note that the constraint matrix of (24)satisfies total unimodularity, thus the binary-valuedwecan be relaxed to be continuous without any compromise [3]. Thus,the budgeted DDUS forweis constructed as
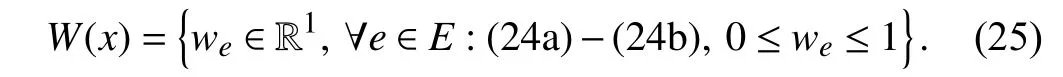
To verify the post-disaster connectivity fromOtoDas well as find the path fromOtoDwith minimal traversal costs after the disaster, the following second-stage optimization problem is considered:
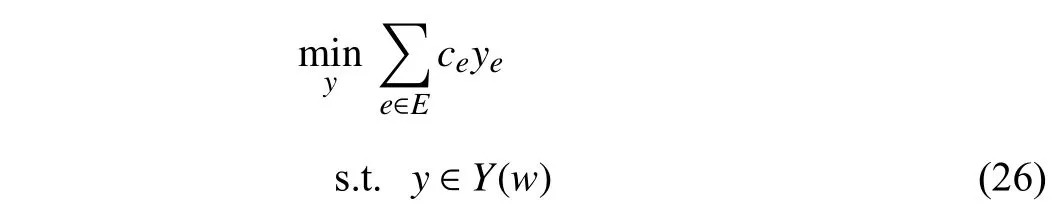
whereY(w)⊆R|E|is defined through the following constraints:

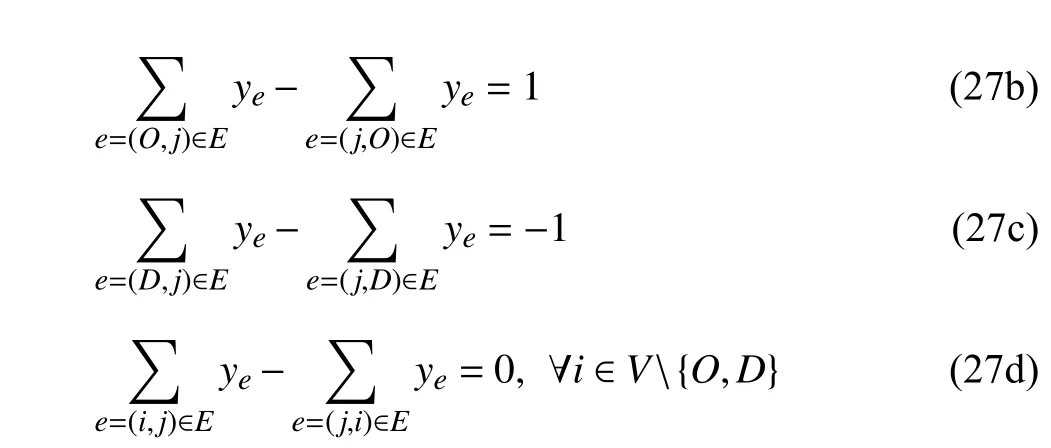
andce∈R1denotes the length of linke. The objective is to minimize the traversal cost fromOtoDin the network. The wait-and-see decision variableye∈{0,1}1takes the values of 1 if the path fromOtoDgoes through linkeand 0 otherwise.Note that in (27), the binary-valuedyeis substituted by its continuous relaxation (27a) since the constraint matrix ofysatisfies total unimodularity property. There exists a path fromOtoDafter the occurrence of the disaster if and only if (26)has at least one feasible solution and the optimal solution to(26) implies the path with least traversal cost fromOtoDin the network.
Next, the mathematical formulation of the two-stage robust pre-disaster highway network investment problem is given
whereae∈R1denotes the investment cost of linke.W(x) andY(w)are defined in (25) and (27), respectively. The objective is to minimize the traversal costs between the O-D pair under the worst-case uncertainty realization as well as the necessary investment cost. Constraint (28c) guarantees the existence of at least one path fromOtoDafter the disaster under any realization ofwin the uncertainty setW(x). The proposed modified Benders dual decomposition algorithm is applied to solve problem(∑28).Notethat givenavariableλ∈R1, thebilinear item λ⎿ψe∈E(1−xe)」 canbepreciselylinearized,thus the robust counterpart of the master problem in Algorithm 1 can be formulated into an MILP problem.
2)Basic Results:The computational results are based on a network with 8 nodes and 9 links, as demonstrated in Fig. 3.The relevant data are from [28]. The traversal costs (lengths)and investment costs of links are provided in Table I. The O-D pair is chosen as (1,6), i.e.,O=1,D=6. For the nominal 9-link network, there are 4 possible paths fromOtoD, as listed in Table II. If all links remain functional, the shortest path fromOtoDis Path 1 (1-3-5-9) with a length of 13.52. The program runs on an Intel Core-i5 1.6-GHz computer and is coded with YALMIP. CPLEX 12.6.0 is utilized as the solver.
The proposed modified Benders dual decomposition algorithm is applied with an initialization ofUB0=4000,LB0=0, ε=0.01, ψ=0.3. The algorithm reaches convergence ofUB=LB=1100.65 after 8 rounds of iterations and the evolution process ofUBkandLBkis shown in Fig. 4. The optimal robust investment (the here-and-now decision) is on Link 3, Link 8, and Link 9. For all possible network realizations under this pre-disaster investment scheme, the worst-case is the failure on Link 5 after the earthquake. In that case, the shortest post-disaster path fromOtoD(the waitand-see decision) is Path 3 with a length of 20.65. The correctness of the computational results can be verified by enumeration.
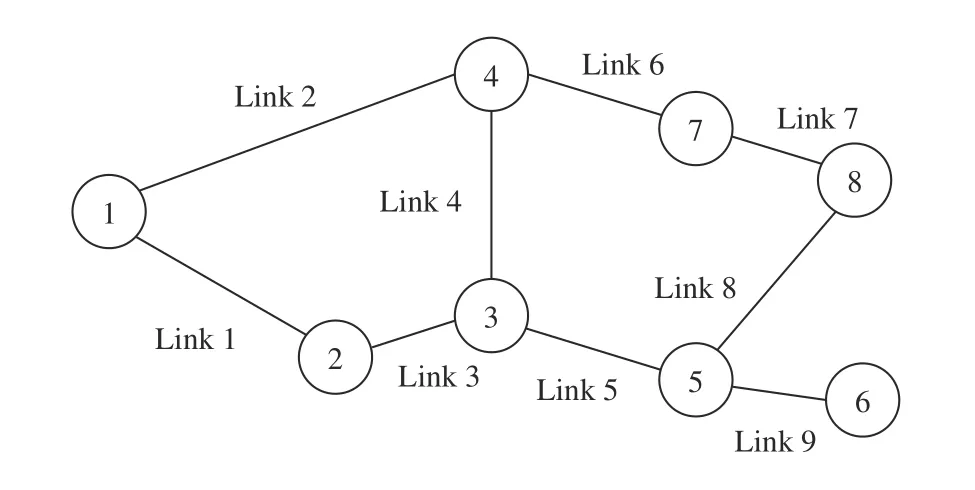
Fig. 3. The 8-node 9-link network.

Link e 1 2 3 4 5 6 7 8 9 ce 6.41 8.09 1.97 6.35 2.87 4.11 2.27 3.91 2.27 ae 500 620 160 780 260 220 500 120 800
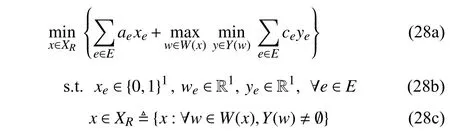
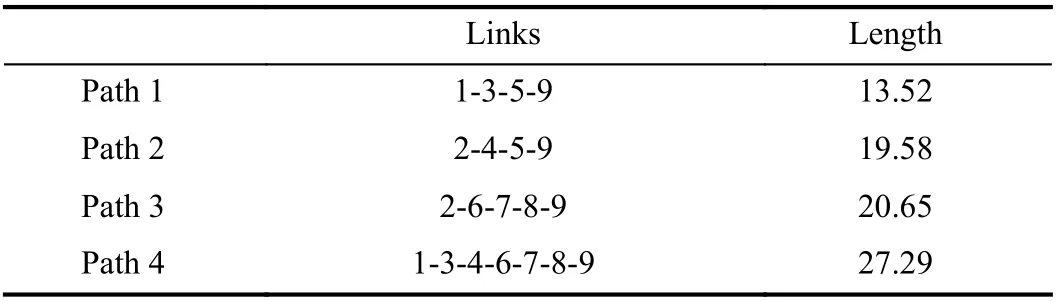
TABLE II PATHS FOR O-D PAIR (1,6)
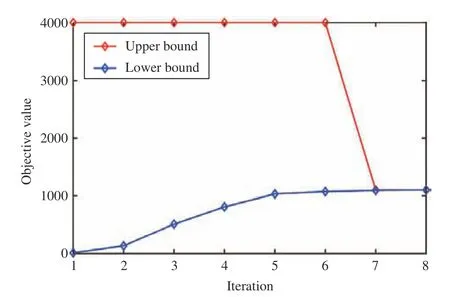
Fig. 4. Evolution of the U Bk and L Bk .
3)Comparative Study:To emphasize the necessity and superiority of the proposed algorithm for DDU-involved twostage RO problems, existing cutting plane algorithms that are theoretically applicable to only the case of DIUs are adopted to solve the same problem in (28). In both the classical Benders decomposition algorithm and the C&CG algorithm,the master problem becomes infeasible at the second round,then the solution procedure interrupts without convergence.This is because the worst-case uncertainty realization identified on the first round is a failure in Link 9, under which there is no path fromOtoD. This situation can be eliminated by strengthening Link 9; however, the invalid feasibility cutgenerated with this concrete scenario is appended to the master problem and the consequent infeasibility falsely implies that there is no feasible solution to the original problem (28). The observations in this comparative case study verify the statements in Remark 2.

TABLE III IMPACT OF ROBUSTNESS PARAMETER ψ
4)Sensitivity Analysis:We present the impact of robustness budgetψon the optimal solution to problem (28). In this case,7 robustness parametersψfrom 0 to 0.6 with a gradient of 0.1 are introduced and the results are displayed in Table III. It is observed that, asψincreases, the optimal objective value including investment costs and worst-case traversal costs increases accordingly. This is because the decision maker has to enhance more links to hedge against the increasing uncertainties on link failures. However, the optimal predisaster investment saturates whenψis greater than or equal to 0.5. This is due to the fact that no matter how largeψis,there always exists a path between the O-D pair if links 1,3,5,9 (Path 1) are all reinforced.
5)Out-of-Sample Analysis:Finally, an out-of-sample analysis is carried out to verify the performance of the robust investment decision. Steps of the out-of-sample assessment areasfollows [29]:a)Consideringallpossible statesofthe 9 links,wegenerate29=512scenarios, namelywo∈{0,1}9,o∈[512]. b) Givenx∗derived by solving (28), for each scenarioo, the following relaxed second-stage problem is solved:

where non-negative slack variablesso+,so−are introduced to the flow conservation constraints (29d)–(29f) and penalized in the objective (29a). The penalty cost coefficientP∈R1is set as 5000 in this case. Problem (29) is a modified version of the second-stage problem (26) with a given here-and-now decisionx∗andthegiven uncertaintyrealizationwo. Denote the solutionto(29)byyo∗,so+∗,so−∗.c)Atlast,the average sampled second-stage costCavand the average sampled infeasibility levelsavare computed as follows:
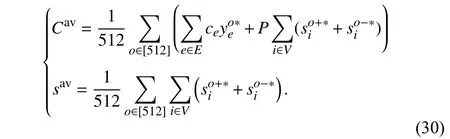
Table IV shows the out-of-sample assessment results for the robust optimal solution under different values of the robustness budgetψ. It is observed thatCavandsavdecrease with the increasingψ, indicating that a biggerψleads to a more robust solution that can hedge against a higher level of uncertainties, but also accordingly generates higher investment cost in the first stage. Comparison with the deterministic model is also provided in Table IV . We can see that disregarding uncertainty would give rise to significantly high second-stage costs (due to the penalty on the slack variablesand)andinfeasibilitylevel.By choosingaproper r obustnessbudgetψ,the decisionmaker can achievethetradeoff between the first-stage investment costs and the secondstage feasibility level.
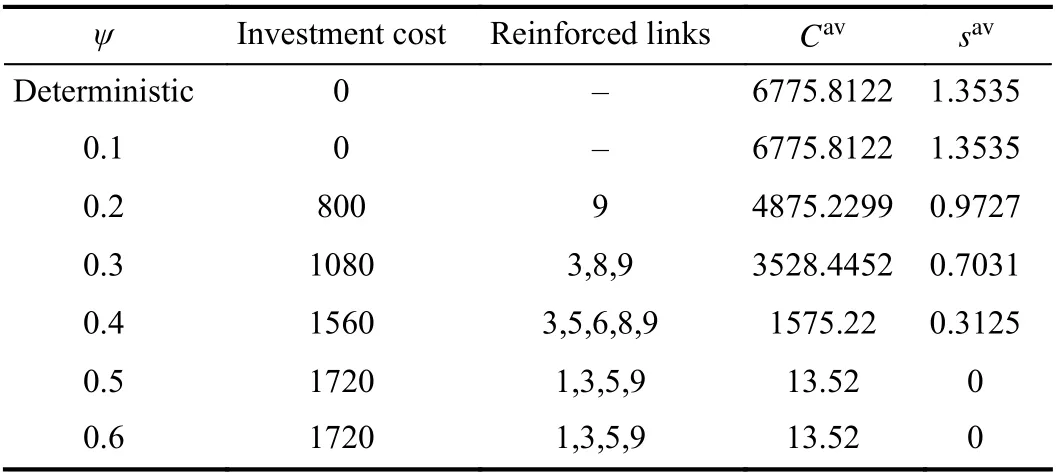
TABLE IV RESULTS FROM THE OUT-OF-SAMPLE ANALYSIS
VI. CONCLUSIONS
In this paper, a novel two-stage RO model with DDUs is proposed. We introduce a class of polyhedral DDUSs whose right-hand-side vectors are in a dependency of the here-andnow decision. Solution methodology for the problem is designed based on modified Benders decomposition, robust counterpart derivation, and linearization techniques. Computational tractability and convergence performance of the proposed algorithm is guaranteed by a strict proof.
Case studies on the pre-disaster highway network investment problem verify that the proposed DDU-incorporated two-stage RO model is an amenable framework for addressing decision-making problems under endogenous uncertainties.The optimality and feasibility of the robust solution are validated by enumeration in this case. Furthermore, the computational studies elucidate that the DDU-involved twostage RO model inherently captures the trade-off between uncertainty mitigation (line investment) and the corresponding expenses (line investment costs) and provides less conservative robust results.
Though we focus on polyhedral DDUS whose right-handside vector has a general correlation with the here-and-now decision, the proposed solution framework based on the modified Benders decomposition in Section III is also applicable to DDUSs with ellipsoidal or conic structure. The limitation of the work in this paper lies in the fact that the duality-based Benders decomposition is conditional upon the second-stage problem which is an LP. Also, uncertain parameters that are of discrete or binary nature would prohibit us from formulating the robust counterpart of the master problem as described in Section IV. These issues remain to be addressed in our future study. In addition, as an extension of this work, future study could combine the optimality and feasibility cuts (9c) and (9d) with the so-called Pareto cuts[30], or extend the robust counterpart (17) to incorporate primal cuts with recourse decision variables in the primal space, to further improve the convergence rate in practice.
APPENDIX
Before we give the proof of Theorem 1, a crucial lemma is provided as follows.
Lemma 2:Letx∗denote the optimal solution to TRO-DDU problem (1). For anyk∈Z+:

Since the TRO-DDU problem (1), problem (8) and problem(31) are equivalent,f(x∗)+S(x∗) is also the optimal objective value of (31). Also note that the master problem (9) is a relaxation to minimization problem (31) since∈Ufor allj∈[ku] and∈Π for allj∈[kπ]. Thus, the optimal objective value of problem (9), which is denoted byLBk, is less than or equaltotheoptimal objective value of problem (31), i.e.,LBk≤f(x∗)+S(x∗).
Recall the updating rule of the upper bound which isUBk=UBk−1whenR(xk)>0 andUBk=f(xk)+S(xk) whenR(xk)=0 . Next, we proveUBk≥f(x∗)+S(x∗) by induction.First of all,UB0=M>f(x∗)+S(x∗). Suppose for the sake of induction thatUBk−1≥f(x∗)+S(x∗) wherek∈Z+. Then, ifUBk=UBk−1, we haveUBk≥f(x∗)+S(x∗) directly. Else ifUBk=f(xk)+S(xk) whenR(xk)=0, then we haveUBk=f(xk)+S(xk)≥f(x∗)+S(x∗) sincexkis a feasible solution to the TRO-DDU problem (1) (by recalling thatxk∈XRif and only ifR(xk)=0 ) andf(x∗)+S(x∗) is the optimal objective value of TRO-DDU problem (1).
Assertion b):∈vert(Π) canbeeasily verified bynoting thattheoptimalsolutionofabi-linear programwith polyhedral feasible region can be achieved at one of the vertices of the polytopes [31].

which contradicts with (33).
Assertion c):Similarly to the proof of Lemma 2–b),∈vert(U)can be verified by noting that the optimal solution of bi-linear programming over a polytope can be achieved at one of its vertices.Suppose there existj1,j2∈[ku] andj1≠j2such that=. We assume thatis the optimum toS(xk j1) andis the optimum toS(xkj2). Without loss of generality, we assume thatj1 then, we have which is equivalent to Recalling the updating rule of lower bound, we have wherei) comes from the relationship in (38),ii) comes from the fact that=,iii) comes from the fact thatis the optimum toS(xk j2), andiv) comes from the updating rule of the upper bound. Thus, we haveUBk j2 ≤LBk j2. According to Lemma 2-a),LBk j2 ≤f(x∗)+S(x∗)≤UBk j2. Thus, we haveLBk j2 =UBk j2 =f(x∗)+S(x∗)and the Algorithm 1 terminates at iterationkj2. This completes the proof of the statement in Lemma 2-c). ■ The proof of Theorem 1 is given as follows. Proof of Theorem 1:First, we prove that Algorithm 1 terminates within a finite round of iterations through a complete enumeration of the vertices of the polyhedral feasible regions of the dual multipliers. According to Lemmas 2-b) and 2-c), no vertex of Π orUwill be appended twice to the master problem. Thus, the termination condition must be met within O (p+q) iterations. Next, we prove the feasibilityofsolutionxk.Sincexkis ge nerated through master problem(9),xk∈X. Moreover,since Algorithm 1 terminates withR(xk)=0 , wehavexk∈XRbyrecallingthatx∈XRif and only ifR(x)=0. Thus,xk∈X∩XR. Finally, we prove the optimality of solutionxk. According to Lemma 2-a),LBk≤f(x∗)+S(x∗)≤UBk. Together with the fact that the Algorithm 1 terminates with |UBk−LBk|<ε andR(xk)=0 , we have |UBk−f(x∗)−S(x∗)|<ε. Recalling thatUBk=f(xk)+S(xk), we have|f(xk)+S(xk)−f(x∗)−S(x∗)|<ε, which justifies the optimality ofxk.■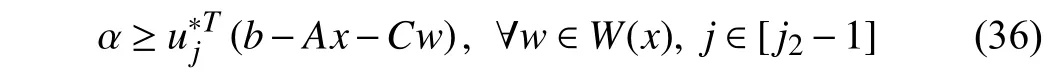
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- An Overview and Experimental Study of Learning-Based Optimization Algorithms for the Vehicle Routing Problem
- Towards Long Lifetime Battery: AI-Based Manufacturing and Management
- Disagreement and Antagonism in Signed Networks: A Survey
- Finite-Time Distributed Identification for Nonlinear Interconnected Systems
- SwinFusion: Cross-domain Long-range Learning for General Image Fusion via Swin Transformer
- Real-Time Iterative Compensation Framework for Precision Mechatronic Motion Control Systems
