Input-to-State Stabilization of Nonlinear Impulsive Delayed Systems: An Observer-Based Control Approach
2022-07-18YuhanWangXiaodiLiandShijiSongSenior
Yuhan Wang,,, Xiaodi Li,,, and Shiji Song, Senior,
Abstract—This paper addresses the problems of input-to-state stabilization and integral input-to-state stabilization for a class of nonlinear impulsive delayed systems subject to exogenous disturbances. Since the information of plant’s states, time delays, and exogenous disturbances is often hard to be obtained, the key design challenge, which we resolve, is the construction of a state observer-based controller. For this purpose, we firstly propose a corresponding observer which is independent of time delays and exogenous disturbances to reconstruct (or estimate) the plant’s states. And then based on the observations, we establish an observer-based control design for the plant to achieve the inputto-state stability (ISS) and integral-ISS (iISS) properties. With the help of the comparison principle and average impulse interval approach, some sufficient conditions are presented, and moreover, two different linear matrix inequalities (LMIs) based criteria are proposed to design the gain matrices. Finally, two numerical examples and their simulations are given to show the effectiveness of our theoretical results.
I. INTRODUCTION
AS an important subclass of hybrid systems, impulsive systems consist of three main components: An ordinary differential equation, a difference equation, and an impulsive law [1], [2]. These systems have drawn considerable attention due to their wide applications in many challenging areas such as networked control systems [3], multi-agent systems [4],optimization problems [5], etc. In addition, time delays are ubiquitous in many fields of science and engineering and might bring about undesired dynamics such as oscillation,instability, and some complicated phenomena, see [6]–[12].Consequently, considering the fact that many dynamical systems are affected by impulsive effects and time delays,stability properties of such systems which are also called impulsive delayed systems have been extensively investigated, see [13]–[20].
In the past decades, the concept of input-to-state stability(ISS), firstly introduced by Sontag in [21] and then extended to delayed systems by Teel in [22], plays an important role in characterizing the influences of external inputs on nonlinear systems. Roughly speaking, the ISS property implies that a system can be asymptotically stable in input-free case and it also has bounded state under bounded input. As a natural generalization of ISS, integral-ISS (iISS) is a weaker but still very meaningful concept, see [23]. Recently, the problems of ISS and iISS were investigated for (delay-free) impulsive systems in [24]–[26] and were subsequently also studied for impulsive delayed systems in [14], [16], [17], [20]. For example, [24] firstly developed the ISS-Lyapunov function method to impulsive systems with external inputs affecting both the continuous dynamics and discrete dynamics, [14]established Razumikhin-type theorems for ISS and iISS of a class of impulsive delayed systems, and [20] investigated the ISS property of time-delay systems subject to delayed impulse effects. Another interesting topic that has been investigated extensively is the input-to-state stabilization problems, that is,designing control laws for plants such that the closed-loop systems achieve the ISS property with respect to exogenous disturbances, see [27], [28]. In particular, [29], [30] studied the input-to-state stabilization of nonlinear systems from impulsive control point of view. However, there is no result for input-to-state stabilization that takes into account the effects of impulsive perturbations and time delays. It is,therefore, important and necessary to design a control scheme for impulsive delayed systems to achieve ISS from impulsive perturbation point of view.
It is well known that the full state information of practical systems might not be completely measurable due to the limitation of implementation cost or measurement technology,which implies that the state feedback is generally limited in control engineering. To this end, numerous interesting works have considered the observer-based output feedback control approach, that is, a sort of dynamic output feedback control approach that can estimate plant’s states online, see [31]–[33].Recently, such control approach has been widely studied for impulsive systems. For example, [34] proposed an observerbased fault-tolerant control method for a class of hybrid impulsive systems, [35] studied robust stabilization for a class of linear impulsive systems, and [36] solved the observerbased quasi-synchronization problem of delayed dynamical networks with impulsive effects. However, it should be noted that when the impulsive systems involve unmeasurable time delays and unknown exogenous disturbances, the abovementioned results are infeasible. Since such undesirable factors may complicate the problems of stability analysis,state estimation, and controller design, it is natural to ask whether it is possible to design an observer-based controller for impulsive systems involving unmeasurable time delays to achieve the ISS performance with respect to exogenous disturbances. So far, to the authors’ best knowledge, this problem has not been fully investigated yet, and remains to be challenging, which motivates our present work.
Statement of Contributions:Motivated by the above discussions and practical requirements, our primary interest in this paper is to design observer-based controllers for input-tostate stabilization of a class of nonlinear impulsive systems with unmeasurable time delays and unknown exogenous disturbances. Based on the comparison principle and average impulse interval approach, some stability criteria are derived and the observer-based output feedback controllers are correspondingly designed. The effectiveness of the developed results is illustrated by numerical simulations. The main contributions of this paper are summarized as follows.
1) Differently from the classical state observers for timedelay systems in [31], [33], [36], [37], in which the construction of the state observers depends on the full information of time delays, the state observer proposed in this paper is delay-independent and can be applied to the case involving unavailable and unmeasurable time delays.
2) The observer-based control for ISS of impulsive systems has been extensively studied, such as [30]–[35]. However,those results cannot be applied to the case involving both time delays and exogenous disturbances. While in this paper, some ISS results have been obtained, in which an observer-based output feedback controller which does not need the full information of time delays and exogenous disturbances has been designed.
3) In order to design the gain matrices of observer-based output feedback controllers conveniently, two different design schemes are proposed in terms of linear matrix inequalities(LMIs), which can be implemented in different cases.
The remainder of this paper is organized as follows. In Section II, we precisely explain the type of systems considered and provide the relevant notations, assumptions, definitions, and lemmas. Main results are proposed in Section III.Two numerical examples are given in Section IV to show the effectiveness of the proposed design. Finally, Section V concludes the paper.
II. PRELIMINARIES
Notations:We use the common definition of class K, K∞,and KL functions from [38]. Let R denote the set of real numbers, R+the setofnonnegativereal numbers,Z+thesetof positive integer numbers, RnandRn×mthen-dimensionalandn×m-dimensional real spaces equipped with the Euclidean norm ||·||, respectively, λmax(A) and λmin(A) the maximum and minimum eigenvalues of symmetric matrix A,respectively. A>0 or A<0 denotes that the matrix A is a symmetricandpositiveornegativedefinitematrix. The notations AT, A−1denotethetransposeandtheinverse ofA,respectively.Iis the identity matrix with appropriate dimensions and ⋆ denotes the symmetric block in one symmetricmatrix.ForanyintervalS1⊆RandanysetS2⊆Rk,1≤k≤2n, we putPC(S1,S2)≜{υ:S1→S2is continuous everywhere except at finite number of pointst, at which υ(t−), υ(t+) exist and υ(t+)=υ(t)}. Fora,b∈R,a
Considerthe following nonlinearimpulsivedelayedsystem:
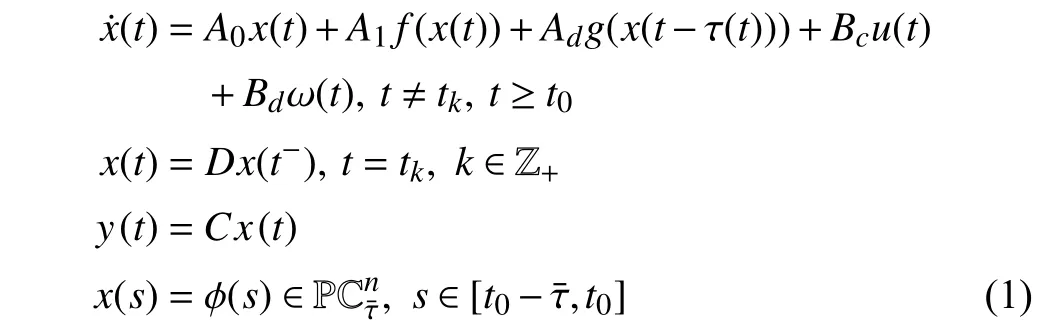
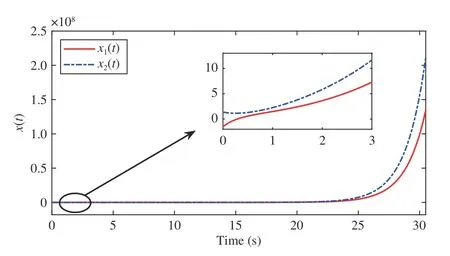
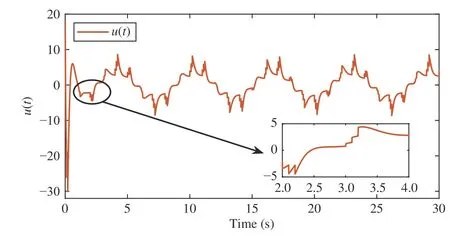
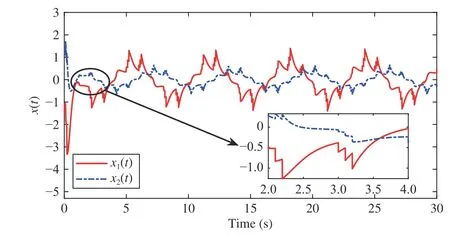
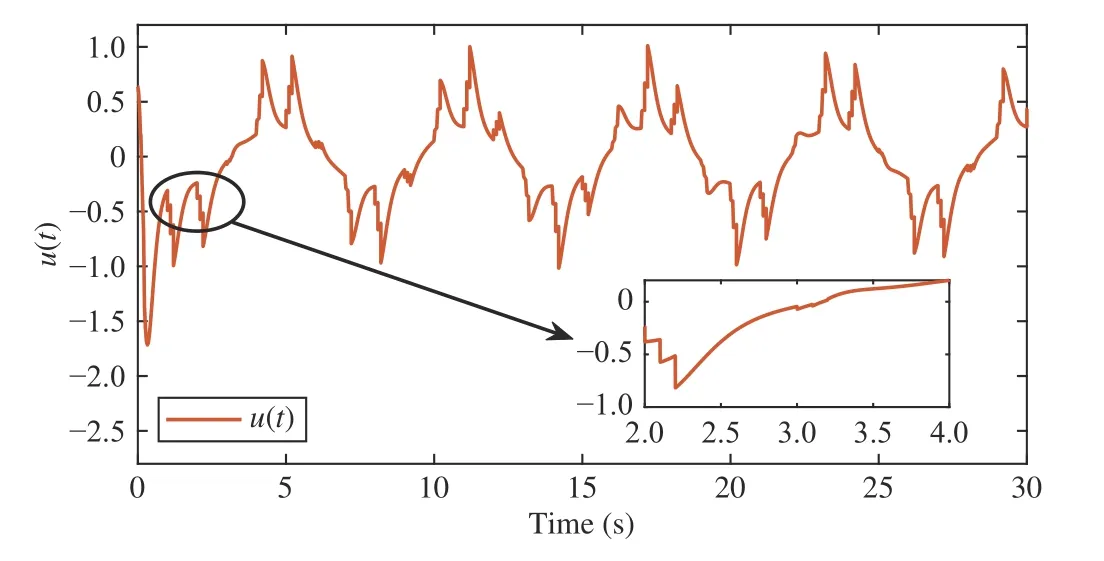
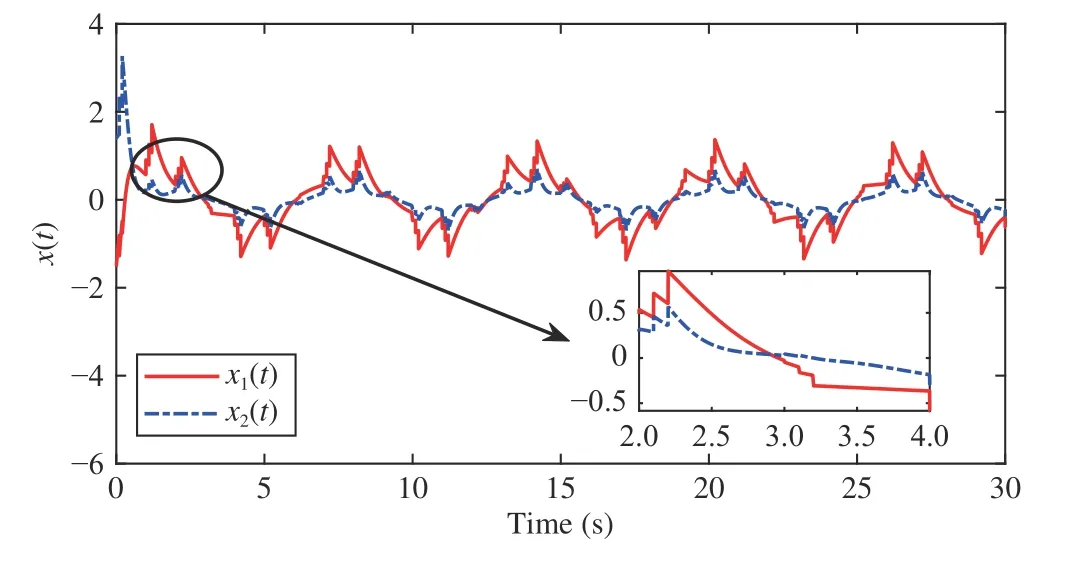
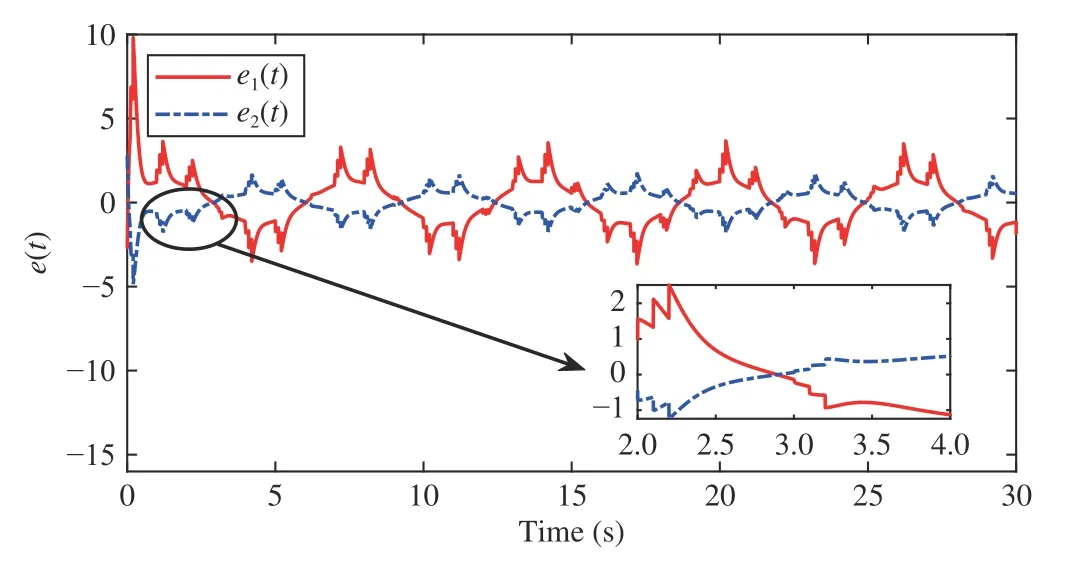
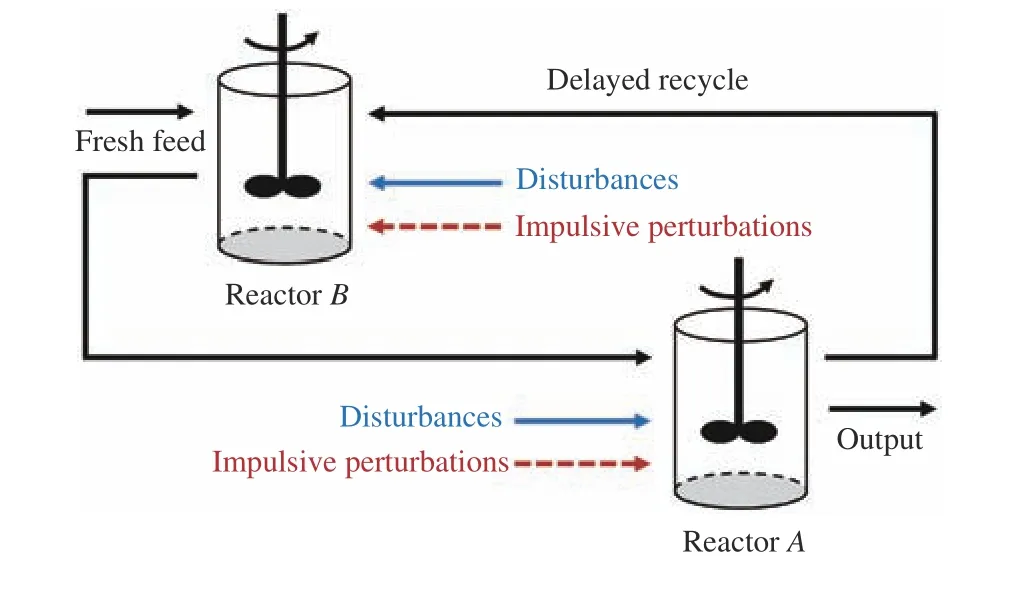
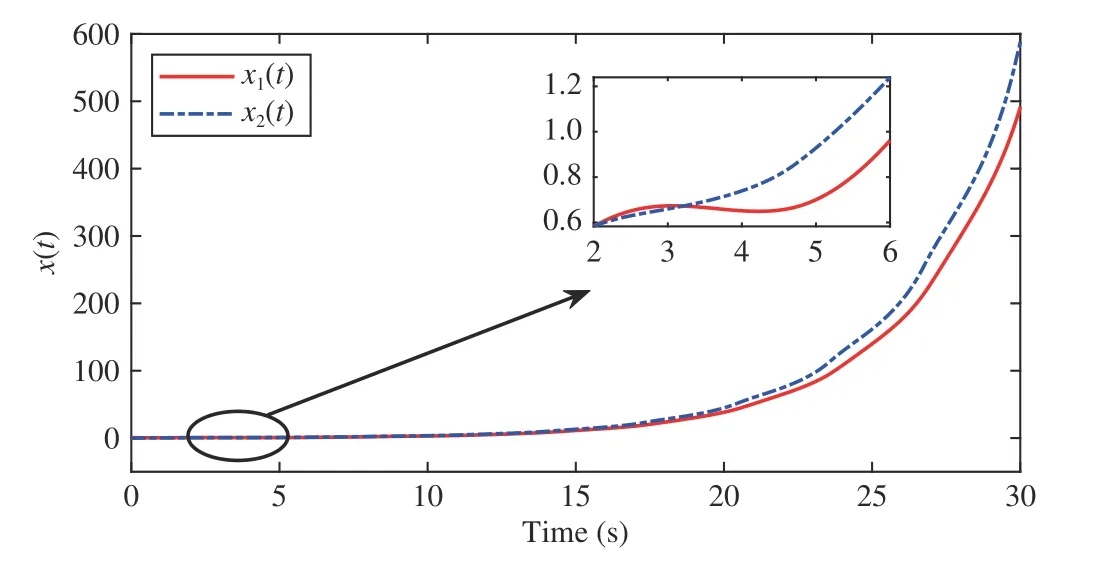
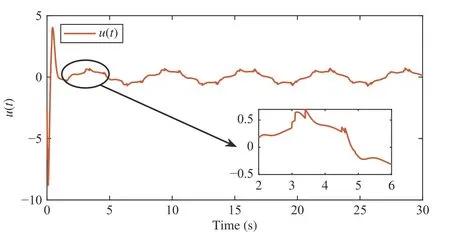
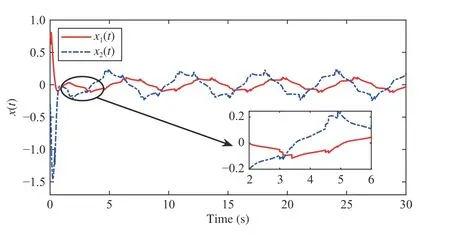
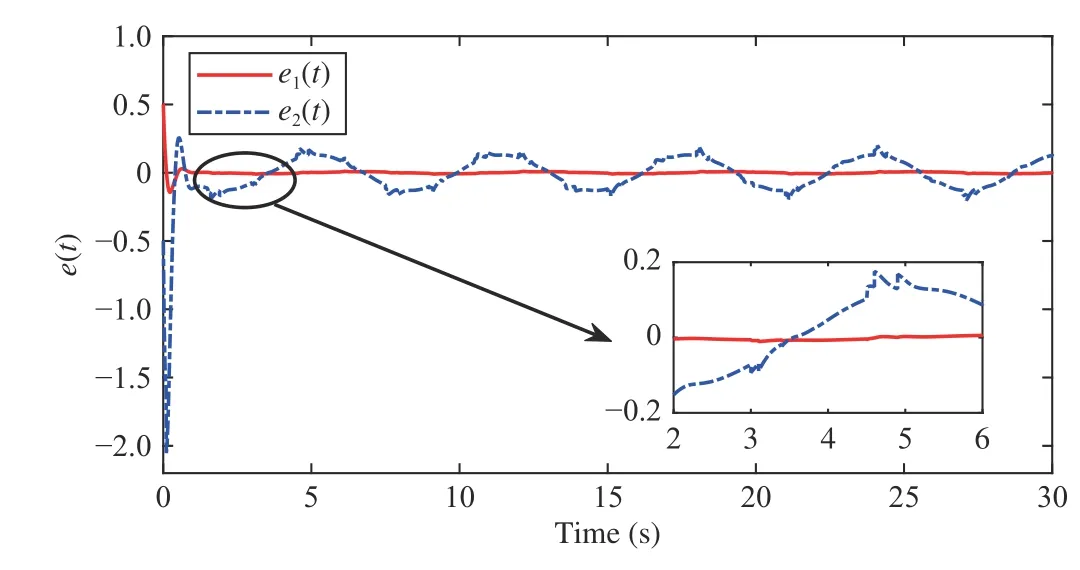
wherex(t)∈Rnis the state,x˙(t) is the upper right-hand derivative ofx(t),u(t)∈Rqis the control input, ω(t)∈Rnis the bounded exogenous disturbance, andy(t)∈Rmis the output (or measurement) withm≤n;A0∈Rn×n,A1∈Rn×n,Ad∈Rn×n,Bc∈Rn×q,Bd∈Rn×n,C∈Rm×n, andD∈Rn×nare constant matrices; τ(t) is the time-varying delay satisfying τ(t)∈[0, τ¯] with τ¯>0;f(x(·))=(f1(x1(·)),...,fn(xn(·)))T∈Rnandg(x(·))=(g1(x1(·)),...,gn(xn(·)))T∈Rnare the nonlinear functions satisfying certain conditions which will be given later. To prevent the occurrence of accumulation points, such as Zeno phenomenon, we only consider that the impulse time sequence {tk}k∈Z+satisfies 0 ≤t0 Assumption 1:For nonlinear functionsfandg, the structure isknown, andtherearepositiveconstantsandsuch that|fj(s1)−fj(s2)|≤|s1−s2|and |gj(s1)−gj(s2)|≤|s1−s2|for alls1,s2∈R,j=1,...,n. In particular,f(0)=g(0)=0.DenoteLf=diag() andLg=diag() for later use. In general, the plant’s states might not be fully available due to the physical limitation or the implementation cost [32],[37], which means that it is very hard to apply a full state feedback control for the plant in such case. Thus, a state observer can be constructed to estimate the plant’s states by utilizing the available measurements. In this paper, the assumption and processing of nonlinear part are not new [39],[40], but we consider the case that the information of time delays and exogenous disturbances cannot be completely obtained. To this end, we firstly consider the following state observer which is independent of time delays and exogenous disturbances: whereK∈Rq×nis the control gain matrix to be designed.Under control input (3), the plant can be rewritten as wheree(t)≜x(t)−(t) is the estimation error between the plant and the observer. It then follows from systems (2) and(4) that the dynamics of the error system is derived as follows: whereF(e(·))≜f(x(·))−f(xˆ(·)) andG(e(·))≜g(x(·))−g(xˆ(·)).According to systems (2) and (5), we obtain the augmented closed-loop impulsive system as follows: with the following vectors: and the following constant matrices: For further discussion, we introduce some definitions and lemmas. Definition 1 [14]:For given impulse time sequence {tk}k∈Z+,system (1) is said to be stabilized to input-to-state stability(ISS) by controller (3), if there exist functions β ∈KL and γ ∈K∞such that for any ϕ ∈and any exogenous disturbance ω (t), the solutionx(t) of system (4) satisfies Definition 2 [14]:For given impulse time sequence {tk}k∈Z+,system (1) is said to be stabilized to integral-ISS (iISS) by controller (3), if there exist functions β ∈KL and α,γ ∈K∞such that for any ϕ ∈and any exogenous disturbance ω (t),the solutionx(t) of system (4) satisfies Remark 1:The above definitions depend on the choice of the sequence{tk}k∈Z+.However,itisoften ofinterestto characterize ISS(iISS)overclassesof sequences {tk}k∈Z+. To this end, thesystem issaidto bestabilized to uniformly ISS(iISS) over a given class F if the system is ISS (iISS) for every sequence in F with functionsβandγthat are independent of the choice of the sequence, see [24]. Definition 3 [24]:The average impulse interval (AII) of the impulsetime sequence{tk}k∈Z+is said tobe notless than τ∗, if thereexistpositive constantsN0and τ∗such that whereN(T,t) is the number of impulses of the sequence{tk}k∈Z+occurring on the interval (t,T], andN0is the elasticity number. Denote such kind of impulse time sequences by set F+[τ∗,N0]for later use. Lemma 1[16]:Letfunctionsh1(t),h2(t)∈PC([t0−,+∞),R+), and φ(t)∈PC([t0,+∞),R+).If thereexist∈R,∈R+, and∈R+such that and it then holds that for allt≥t0, Remark 2:The proof of Lemma 2 is similar to that in [16].However, one can see that the main difference is that we only need thatis a real constant, which can lead to wider applications. The purpose of this paper is to derive some sufficient conditions for input-to-state and integral input-to-state stabilization of system (1) via observer-based control (2) and(3). To do this, we firstly find sufficient conditions for uniformly ISS (iISS) of system (6), which means that the system (1) is stabilized to uniformly ISS (iISS) under the given observer-based control scheme. The proof is based on Lemmas 1 and 2. Based on (11) and (12), we derive the following comparison system: Assume thatvε(t) is the corresponding maximal solution of system (13) for any given ε >0. Based on Lemma 1, it can be deduced thatV(t)≤v(t)≤vε(t) for allt≥t0. It then follows from Lemma 2 that: for allt≥t0. Using Definition 3, we have where λ3=λ1−lnµ/τ∗>0 and η=µN0. Substituting (13) and(15) into (14) yields that From (16) and (18), we observe that where Then, the following proof is separated into two parts. Part I:In this part, we aim to prove that system (1) is stabilized to uniformly ISS over the class F+[τ∗,N0]. Using(19), we get for allt≥t0, which implies that Remark 3:In particular, if we consider the case thatN0=1,then one can see that the minimal impulse interval is used instead of the average impulse interval, which implies that two consecutive impulse instants must be separated by at leastτ∗units of time. Then, we can derive the following corollary from Theorem 1. Corollary 1:Given matricesK∈Rq×nandL∈Rn×m, if there exist 2n×2nmatricesP>0,R>0, 2n×2ndiagonal matricesQi>0,i=1,2,3,and positiveconstantsτ∗,λ1, λ2,and µ>1,s uchthatτ∗>lnµ/(λ1−µλ2)>0,Q3<λ2P, (9),and(10), then by the observer-based controller (3) with (2),system (1) is stabilized to uniformly ISS (iISS) over the class Fτ∗,where Fτ∗denotesthe class of impulse sequences{tk}k∈Z+satisfyingtk−tk−1≥τ∗. Next, consider the case thatD=Iwith µ>1, we can formulate Theorem 1 as follows. Corollary 2:Suppose thatD= √Iwith µ>1. Given matricesK∈Rq×nandL∈Rn×m, if there exist 2n×2nmatricesP>0,R>0, 2n×2ndiagonal matricesQi>0,i=1,2,3, and positive constantsN0, τ∗, λ1, and λ2, such that τ∗>lnµ/(λ1−µN0λ2)>0 ,LˇT Q3Lˇ<λ2P, and (9), then by the observer-based controller (3) with (2), system (1) is stabilized to uniformly ISS (iISS) over the class F+[τ∗,N0]. Remark 4:In Theorem 1, Corollaries 1, and 2, the matrix inequality (9) is nonlinear, which limits the design of gain matricesKandLvia the MATLAB LMI Toolbox. To overcome this difficulty, two different cases are fully considered and some necessary matrix transformations need to be applied, which leads to the following results. Theorem 2:Suppose that the control input matrixBcis full columnrank.ForgivenpositiveconstantsN0,λ1,λ2,andµ>1,if thereexist apositive constantτ∗,n×nmatricesP1>0,P2>0 ,R1>0,R2>0,n×ndiagonal matricesQij>0,i=1,2,3,j=1,2,and constantmatricesX∈Rn×n,Y∈Rn×m, such thatτ∗>lnµ/(λ1−µN0λ2)>0 ,Q3<λ2P,(10), and where with which means that where with Then, one can see that Next, pre-multiplying and post-multiplying both sides of(21) with, it holds that Remark 5:There have been various results on input-to-state stabilization of linear (nonlinear) systems involving unmeasurable states in the literature, see [30], [34], [35], [37],[41]. Similarly to those results, the output feedback controller we designed is also based on a state observer. One can see that the possible time delays are excluded in [30], [34], [35]. In the framework of time delays, [37] studies the observer-based input-to-state stabilization problem for nonlinear delayed system. However, the state observer proposed in [37] depends on the full information of time delays. That is, the time delays need to be fully available and measurable. Although the observer designed in [41] does not require the full information of network-induced delays, the state delays of system itself are excluded. In this paper, we propose an observer-based controller which can stabilize nonlinear impulsive systems involving unmeasurable time delays and unknown exogenous disturbances to ISS (iISS), where the information of time delays and exogenous disturbances is not needed. Moreover,the destabilizing effects of impulsive perturbations are also considered in this paper, which leads to wider applications. Remark 6:Theorem 2 presents some LMI-based conditions to design observer-based control input u such that system (1)is stabilized to ISS (iISS). When using Theorems 2 and 3, it is necessary to give proper parameters such that inequalities τ∗>lnµ/(λ1−µN0λ2)>0,Q3<λ2P, (10), and (20) hold.Then the feasible solutions of those inequalities, that is,X,Y,P1,P2,R1,R2, andQi j>0,i=1,2,3,j=1,2, can be derived by the MATLAB LMI Toolbox. Based on the above analysis,the gain matrices can be designed by such known matrices and the low bound of the AII constant τ∗can be derived. From the algorithm point of view, since positive constants λ1and λ2describe the possible convergence rate of the Lyapunov functionV, it is desirable to give a larger λ1and a smaller λ2when solving LMIs in Theorem 2. In addition, the positive constant µ>1 describes the possible jump amplitude of the Lyapunov functionVat impulse instants. Thus, a smaller μ is preferred for the feasibility of LMI in (10). Similarly, the above analysis is suitable to Theorem 3. Remark 7:In Theorem 2, we assume that the control input matrixBcis full column rank, which implies thatBcis invertible. Such assumption is crucial for the design of the controller gainK. While in Theorem 3, we assume that the output matrixCis full row rank, which implies thatCCTis invertible. Such assumption is crucial for the design of the observer gainL. One can see that the proposed results in Theorems 2 and 3 can be applied for different cases. Hence,they are different but complementary to each other. Moreover,how to derive some less conservative conditions for the general case is an interesting topic. This issue will be explored in our future work. In this section, we present two numerical examples and relevant simulations to demonstrate the validity of the above designed observer-based control schemes. Example 1:Consider the following nonlinear delayed system: with where the time delay τ(t) is unmeasurable and satisfies τ(t)∈[0 0.2], and the exogenous disturbance ω(t) is unknown but bounded. When there is no control input (i.e.,u(t)=0), by simulation, Fig. 1 shows that the system (23) is not ISS with the choiceofτ(t)=0.2|sint|,ω(t)=[0.8cost1.1sint]T,initial condition [ϕ1(s) ϕ2(s)]T=[−1.5 1.4]Tfors∈[−0.2,0].In the following, we consider two different cases. Fig. 1. Trajectories of x(t) without control input. Case I:The control input matrixBcis full column rank. In this case, we will design the observer-based controller (3) with(2) such that system (23) with the following impulsive perturbations: achieves the ISS property based on Theorem 2. We firstly assume thatBc=[0.5 0.3]TandC=[0 7]. Then, for given λ1=5.8, λ2=0.28 ,µ=2.56,andN0=2,bycalculatingthe rangeofvaluesforτ∗ andsolvingtheLMIs, we obtain τ∗∈(0.2371,+∞) and the following gain matrices: Thus, according to Theorem 2, system (23) and (24) can be stabilized to uniformly ISS over the class F+[τ∗,2] with τ∗∈(0.2371,+∞). For simulations, we take impulse time sequence {tk}k∈Z+={t3n−2=n−0.9,t3n−1=n−0.8,t3n=n}n∈Z+∈F+[1/3,2] and still consider τ(t)=0.2|sint|,ω(t)=[0.8cost1.1sint]T, initial condition [ϕ1(s) ϕ2(s)]T=[−1.5 1.4]Tfors∈[−0.2,0]. Moreover, the observer-based controller (3) with(2) is given with the designed gains in (25). One can see that Fig. 2 shows the control signals, Fig. 3 shows the trajectories of plant states, and Fig. 4 shows the trajectories of observation error signals. The corresponding simulations reflect the validity of our results. Fig. 2. Trajectory of u (t) in Case I. Fig. 3. Trajectories of x(t) under control input in Case I. Fig. 4. Trajectories of e(t) with the initial condition []T =[−2.7 2.8]T in Case I. Case II:The output matrixCis full row rank. In this case,to study the input-to-state stabilization of system (23) and(24), we suppose thatBc=[0 5.2]TandC=[3 6]. If we chooseparametersλ1=5, λ2=0.32,µ=2.56,andN0=2,t hen byTheorem 3,wecan obtain τ∗∈(0.3238,+∞) and Thus, using the above calculated solutions, the ISS property of system (4) is achieved. In simulations, τ(t), ω(t), ϕ(s), and{tk}k∈Z+aresameasthoseinCase I. The corresponding simulationsare shownin Figs. 5–7. Fig. 5. Trajectory of u (t) in Case II. Fig. 6. Trajectories of x(t) under control input in Case II. Fig. 7. Trajectories of e (t) with the initial condition []T =[−2.7 2.8]T in Case II. Example 2:To further demonstrate the flexibility and effectiveness of the proposed design scheme, we consider a chemical reactor system with two reactorsAandB[42], as shown in Fig. 8. Based on mass balances, when there is no impulse, the dynamics of the reactants can be modeled approximately as follows: Fig. 8. Chemical reactor system. wherex1(·) andx2(·) are the compositions;y(t) is the output;kAandkBare the reaction constants; θAand θBare the reactor residence times;rAandrBare the recycle flow rates;vAandvBare the reactor volumes; ϑ is the feed rate; the time delayτ(t)is unmeasurable and satisfies τ (t)∈[0 0.5], and the exogenous disturbances ω1(t) and ω2(t) are unknown but bounded. Some other information on system (26) can be found in [42]. For the chemical reactor system (26), we consider thatkA=1,kB=0.5, θA=θB=2 ,rA=0.5,rB=0.25,vA=vB=0.5, and ϑ=0.5. Then, we obtain the following system: with When there is no control input (i.e.,u(t)=0), by simulation,Fig. 9 shows that the system (27) is not ISS with the choice of τ(t)=0.5|cost|,ω(t)=[0.2sint0.25cost]T,initial condition[ϕ1(s)ϕ2(s)]T=[0.8−0.3]Tfors∈[−0.5,0]. In practice, many chemical reactions are affected by discontinuous perturbations at certain instants, which may lead to sudden changes in the states of the chemical reactor system. To describe it, we consider such sudden changes as the impulsive perturbations in the form of (24). Moreover, due to the complexity of the chemical reactor system, the full information of system states is hard to be obtained. Thus, it is more realistic to design the observer-based controller (3) with(2) for the input-to-state stabilization of system (27) with impulses (24). If we choose parameters λ1=5.7 , λ2=1.6,µ=1.69, andN0=2,thenbyTheorem2,wecan obtain τ∗∈(0.4643,+∞)andthe following gainmatrices: Fig. 9. Trajectories of x(t) without control input. Thus, by using above solutions, the observer-based control inputu(t) can be obtained, which can be used to stabilize system (24)–(27) to ISS. For simulations, we take impulse time sequence{tk}k∈Z+={t3n−2=1.5n−1.4,t3n−1=1.5n−1.1,t3n=1.5n}n∈Z+∈F+[0.5,2] andstill consider τ(t)=0.5|cost|,ω(t)=[0.2sint0.25cost]T,initial condition[ϕ1(s)ϕ2(s)]T=[0.8−0.3]Tfors∈[−0.5,0]. The corresponding control inputu(t)can be found in Fig. 10 . With such control input, the simulation results are shown in Figs. 11 and 12. One can see that the designed controller can render the resulting closedloop system as ISS, which illustrates the effectiveness of the observer-based output feedback control approach. Fig. 10. Trajectory of u (t). Fig. 11. Trajectories of x (t) under control input. Fig. 12. Trajectories of e(t) with the initial condition[]T =[0.5−0.5]T. The paper’s key design idea is how to develop a novel control scheme to stabilize a class of impulsive delayed systems to ISS and iISS when the information of the plant’s states cannot be adequately obtained. We have constructed an observer to estimate the plant’s states and designed an observer-based control scheme for input-to-state stabilization.Using the Lyapunov method and comparison principle, some criteria have been presented for the ISS property of the closedloop system and moreover, the corresponding observer-based controller has been designed. Finally, the advantage and effectiveness of our results have been demonstrated by simulation results. Since practical systems are often affected by the random noises [43], another interesting direction is to develop observer-based control for input-to-state stabilization of impulsive stochastic nonlinear systems.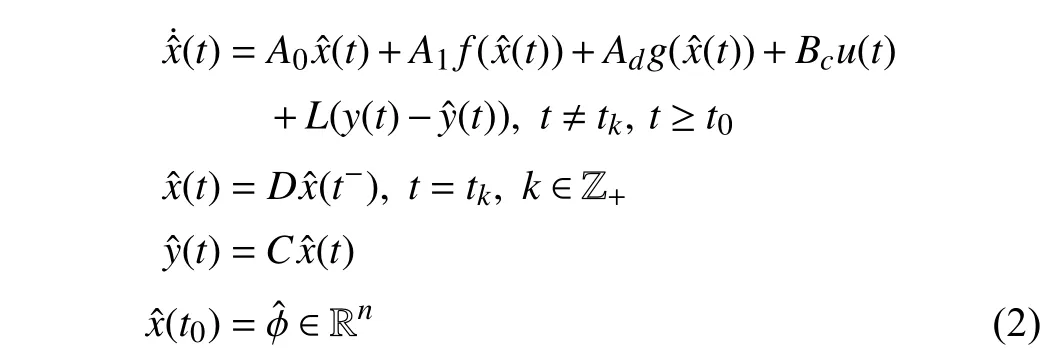
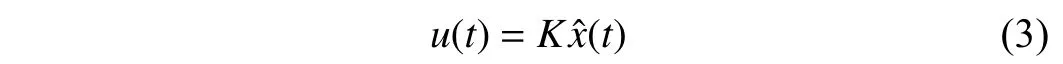
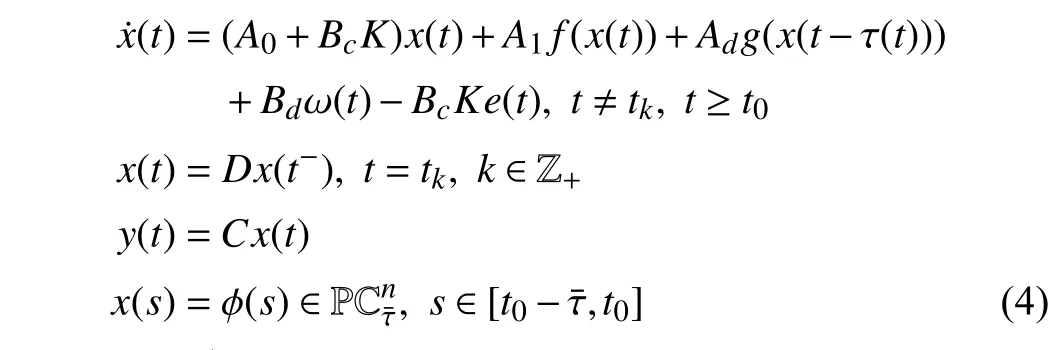
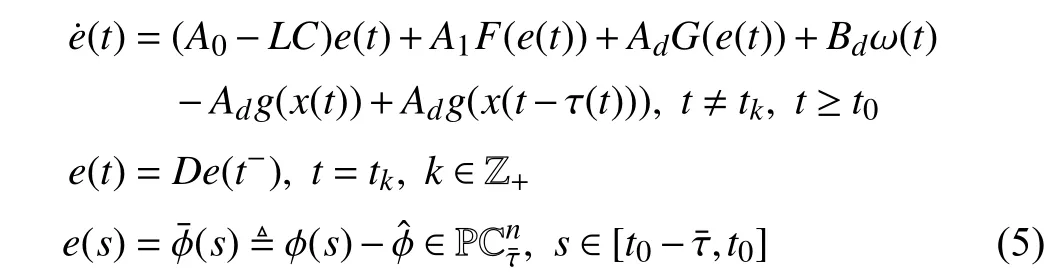
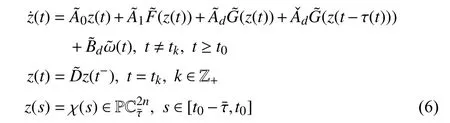
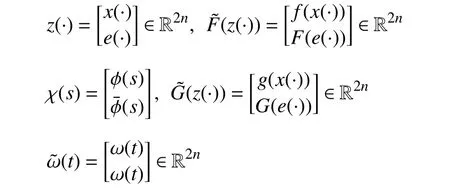
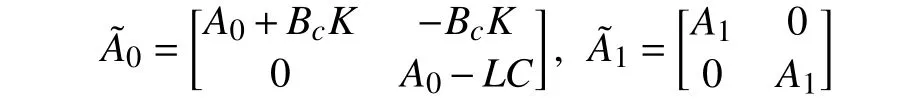
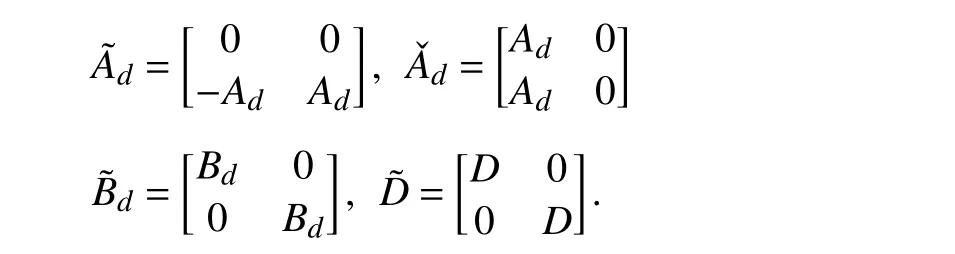
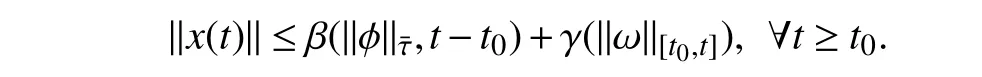


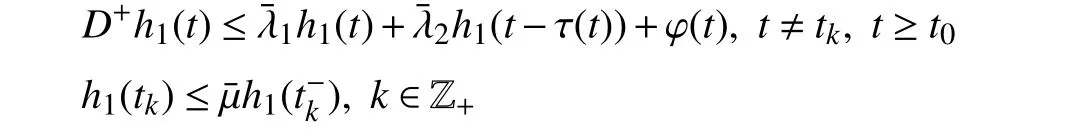
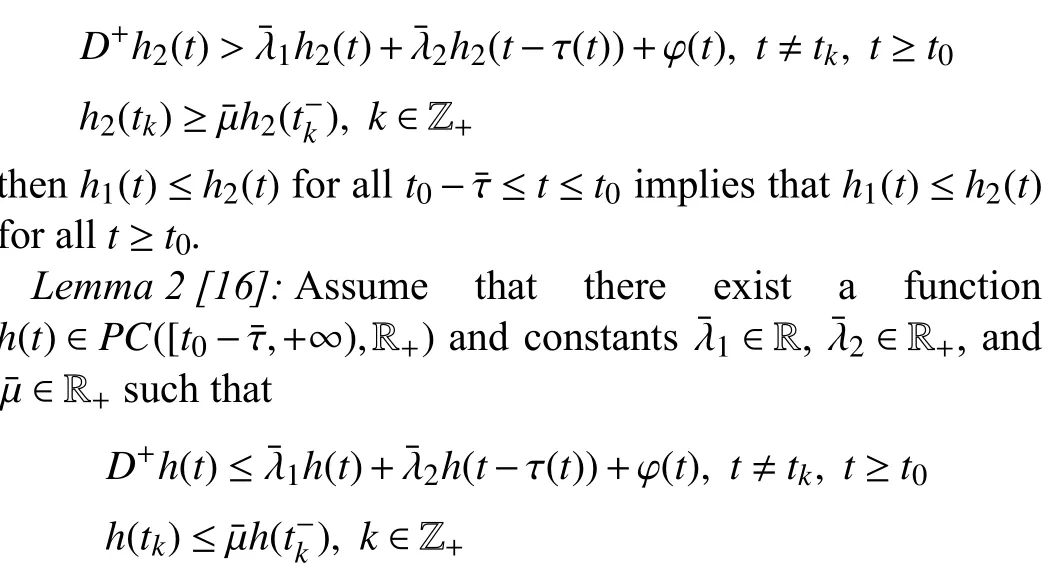
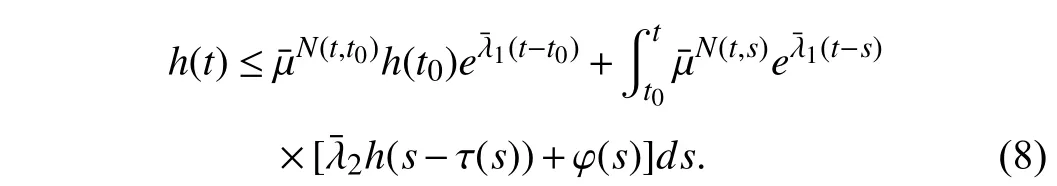
III. MAIN RESULTS

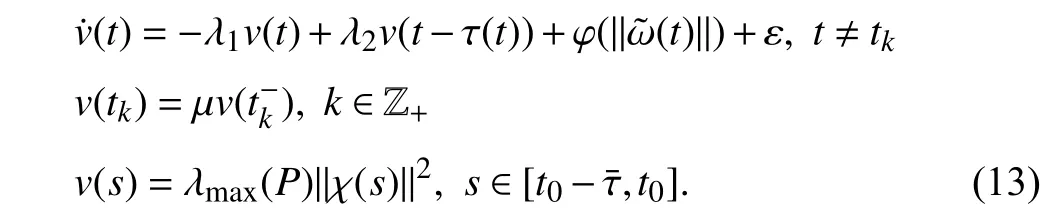
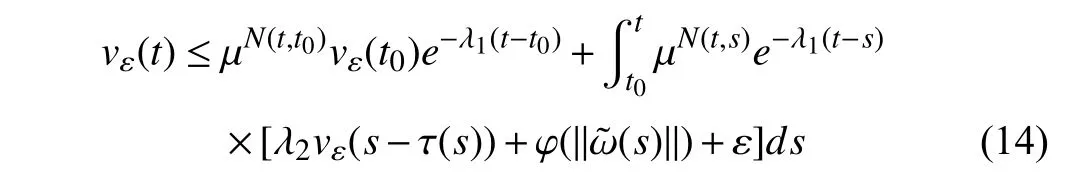
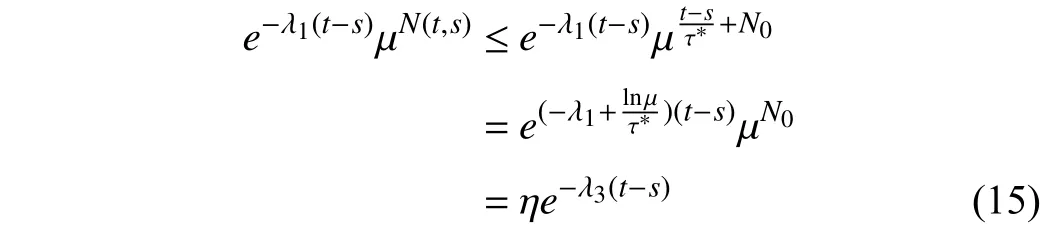

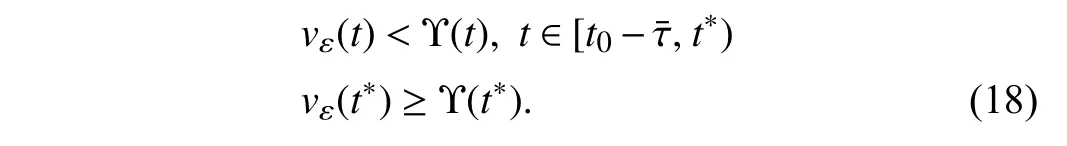
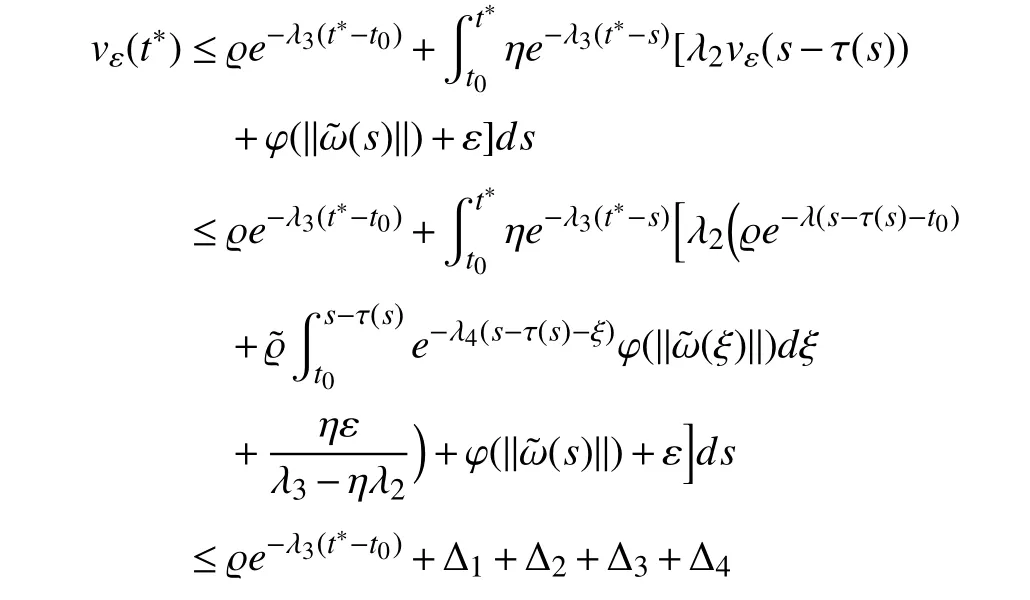



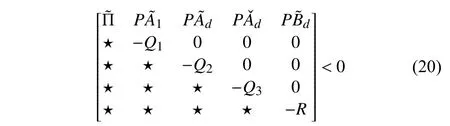
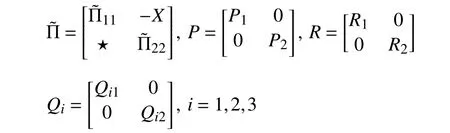

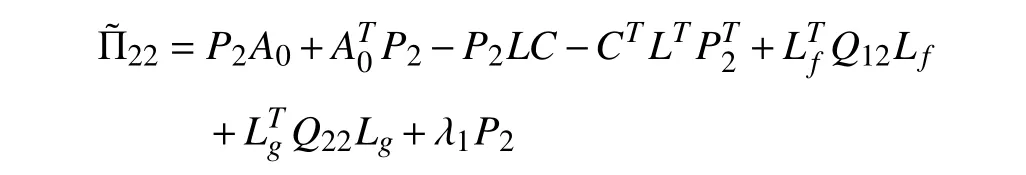





IV. NUMERICAL EXAMPLES


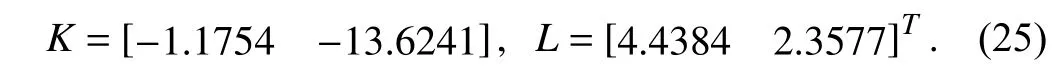

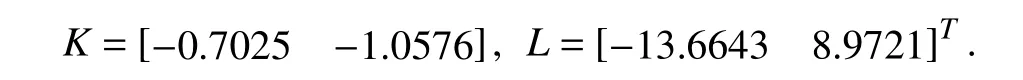
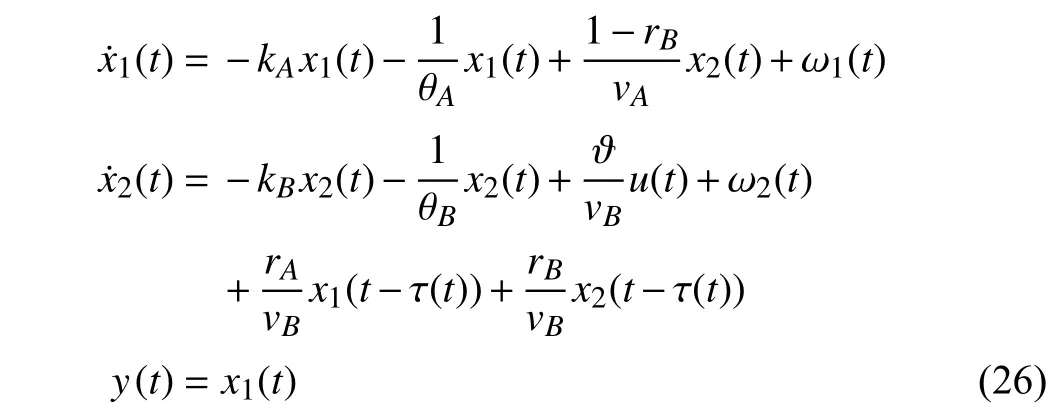

V. CONCLUSIONS
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- An Overview and Experimental Study of Learning-Based Optimization Algorithms for the Vehicle Routing Problem
- Towards Long Lifetime Battery: AI-Based Manufacturing and Management
- Disagreement and Antagonism in Signed Networks: A Survey
- Finite-Time Distributed Identification for Nonlinear Interconnected Systems
- SwinFusion: Cross-domain Long-range Learning for General Image Fusion via Swin Transformer
- Real-Time Iterative Compensation Framework for Precision Mechatronic Motion Control Systems
