Discounted Iterative Adaptive Critic Designs With Novel Stability Analysis for Tracking Control

Mingming Ha, Ding Wang,,, and Derong Liu,,

Abstract—The core task of tracking control is to make the controlled plant track a desired trajectory. The traditional performance index used in previous studies cannot eliminate completely the tracking error as the number of time steps increases. In this paper, a new cost function is introduced to develop the value-iteration-based adaptive critic framework to solve the tracking control problem. Unlike the regulator problem,the iterative value function of tracking control problem cannot be regarded as a Lyapunov function. A novel stability analysis method is developed to guarantee that the tracking error converges to zero. The discounted iterative scheme under the new cost function for the special case of linear systems is elaborated.Finally, the tracking performance of the present scheme is demonstrated by numerical results and compared with those of the traditional approaches.

I. INTRODUCTION

RECENTLY, adaptive critic methods, known as approximate or adaptive dynamic programming (ADP) [1]–[8],have enjoyed rather remarkable successes for a wide range of fields in the energy scheduling [9], [10], orbital rendezvous[11], [12], urban wastewater treatment [13], attitude-tracking control for hypersonic vehicles [14] and so forth. Adaptive critic designs have close connections to both adaptive control and optimal control [15], [16]. For nonlinear systems, it is difficult to obtain the analytical solution of the Hamilton-Jacobi-Bellman (HJB) equation. Iterative adaptive critic techniques, mainly including value iteration (VI) [17]–[20]and policy iteration (PI) [21], [22], have been extensively studied and successfully applied to iteratively approximate the numerical solution of the HJB equation [23]–[26]. In [27],relaxed dynamic programming was introduced to overcome the “curse of dimensionality” problem by relaxing the demand for optimality. The upper and lower bounds of the iterative value function were first determined and the convergence of VI was revealed. For ensuring stability of the undiscounted VI, Heydari [28] developed a stabilizing VI algorithm initialized by a stabilizing policy. With this operation, the stability of the closed-loop system using the iterative control policy can be guaranteed. In [29], the convergence and monotonicity of discounted value function were investigated.The discounted iterative scheme was implemented by the neural-network-based globalized dual heuristic programming.Afterwards, Haet al. [30] discussed the effect of the discount factor on the stability of the iterative control policy. Several stability criteria with respect to the discount factor were established. In [31], Wanget al. developed an event-based adaptive critic scheme and presented an appropriate triggering condition to ensure the stability of the controlled plant.

Optimal tracking control is a significant topic in the control community, which mainly aims at designing a controller to make the controlled plant track a reference trajectory. The literature on this problem is extensive [32]–[37] and reflects considerable current activity. In [38], Wanget al. developed a finite-horizon optimal tracking control strategy with convergence analysis for affine discrete-time systems by employing the iterative heuristic dynamic programming approach. For the linear quadratic output tracking control problem, Kiumarsiet al. [39] presented a novel Bellman equation, which allows policy evaluation by using only the input, output, and reference trajectory data. Liuet al. [40] concerned the robust optimal tracking control problem and introduced the adaptive critic design scheme into the controller to overcome the unknown uncertainty caused by multi-input multi-output discrete-time systems. In [41], Luoet al. designed the modelfree optimal tracking controller for nonaffine systems by using a critic-only Q-learning algorithm, while the proposed method needs to be given an initial admissible control policy. In [42],a novel cost function was proposed to eliminate the tracking error. The convergence and monotonicity of the new value function sequence were investigated. On the other hand, some methods to solve the tracking problem for affine continuoustime systems can be found in [43]–[46]. For affine nonlinear partially-unknown constraint-input systems, the integral reinforcement learning technique was studied to learn the solution to the optimal tracking control problem in [43], which does not require to identify the unknown systems.

In general, the majority of adaptive critic tracking control methods need to solve the feedforward control input of the reference trajectory. Then, the tracking control problem can be transformed into a regulator problem. However, for some nonlinear systems, the feedforward control input corresponding to the reference trajectory might be nonexistent or not unique, which makes these methods unavailable. To avoid solving the feedforward control input, some tracking control approaches establish a performance index function of the tracking error and the control input. Then, the adaptive critic design is employed to minimize the performance index. With this operation, the tracking error cannot be eliminated because the minimization of the control input cannot always lead to the minimization of the tracking error. Moreover, as mentioned in[30], the introduction of discount factor will affect the stability of the optimal control policy. If an inappropriate discount factor is selected, the stability of the closed-loop system cannot be guaranteed. Besides, unlike the regulator problem,the iterative value function of tracking control is not a Lyapunov function. Till now, few studies have focussed on this problem. In this paper, inspired by [42], the new performance index is adopted to avoid solving the feedforward control and eliminate the tracking error. The stability conditions with respect to the discount factor are discussed, which can guarantee that the tracking error converges to zero as the number of time steps increases.

The main contributions of this article are summarized as follows.

1) Based on the new performance index function, a novel stability analysis method for the tracking control problem is established. It is guaranteed that the tracking error can be eliminated completely.

2) The effect of the presence of the approximation errors derived from the value function approximator is discussed with respect to the stability of controlled systems.

3) For linear systems, the new VI-based adaptive critic scheme between the kernel matrix and the state feedback gain is developed.

The remainder of this paper is organized as follows. In Section II, the necessary background and motivation are provided. The VI-based adaptive critic scheme and the properties of the iterative value function are presented. In Section III, the novel stability analysis for tracking control is developed. In Section IV, the discounted iterative formulation under the new performance index for the special case of linear systems is discussed. Section V compares the tracking performance of the new and traditional tracking control approaches by the numerical results. In Section VI, conclusions of this paper and further research topics are summarized.

Notations:Throughout this paper, N and N+are the sets of all nonnegative and positive integers, respectively, i.e.,N={0,1,2,...} and N+={1,2,...}. R denotes the set of all real numbers and R+is the set of nonnegative real numbers. Rnis the Euclidean space of alln-dimensional real vectors.Inand 0m×nrepresents then×nidentity matrix and them×nzero matrix, respectively.C≤0 means that the matrixCis negative semi-definite.

II. PROBLEM FORMULATION AND VI-BASED ADAPTIVE CRITIC SCHEME

Consider the following affine nonlinear systems given by:

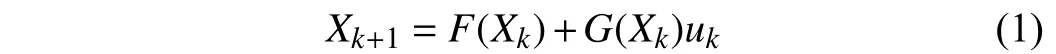
withthestateXk∈Rnandinputuk∈Rm,wheren,m∈N+andk∈N.F: Rn→RnandG: Rn×Rm→Rnarethedriftand control input dynamics, respectively. The tracking error is defined as

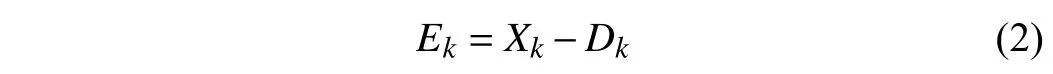
whereDkis the reference trajectory at stagek. Suppose thatDkis bounded and satisfies

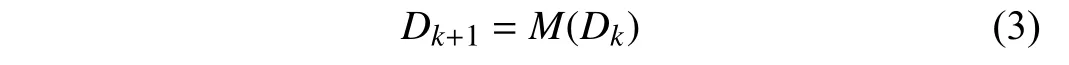
whereM(·) is the command generator dynamics. The objective of the tracking control problem is to design a controller to track the desired trajectory. Letuk={uk,uk+1,...},k∈N, be an infinite-length sequence of control inputs. Assume that there exists a control sequenceu0such thatEk→0 ask→∞.

In general, in the previous works [34], [38], assume that there exists a feedforward control input ηksatisfyingDk+1=F(Dk)+G(Dk)ηkto achieve perfect tracking. However,for some nonlinear systems, the feedforward control input might be nonexistent. To avoid computing the feedforward control input ηk, the performance index [33], [34] is generally designed as

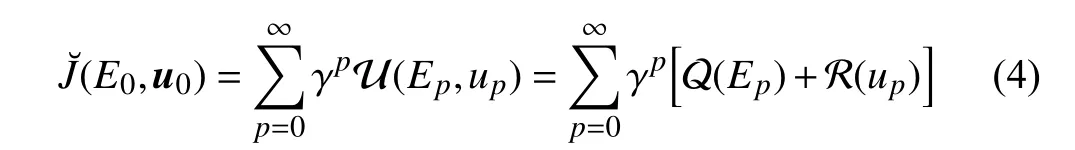
whereγ ∈(0,1]isthe discountfactor and U(·,·)istheutility function.TermsQ: Rn→R+andR: Rm→R+intheutility function are positive definite continuous functions. With this operation, both the tracking error and the control input in the performance index (4) are minimized. To the best of our knowledge, the minimization of the control input does not always result in the minimization of the tracking error unless the reference trajectory is assumed to beDk→0 ask→∞.Such assumption greatly reduces the application scope of the approach. Therefore, for the majority of desired trajectories,the tracking error cannot be eliminated [42] by adopting the performance index (4). According to [42], under the control sequence u0, a new discounted cost function for the initial tracking errorE0and reference pointD0is introduced as

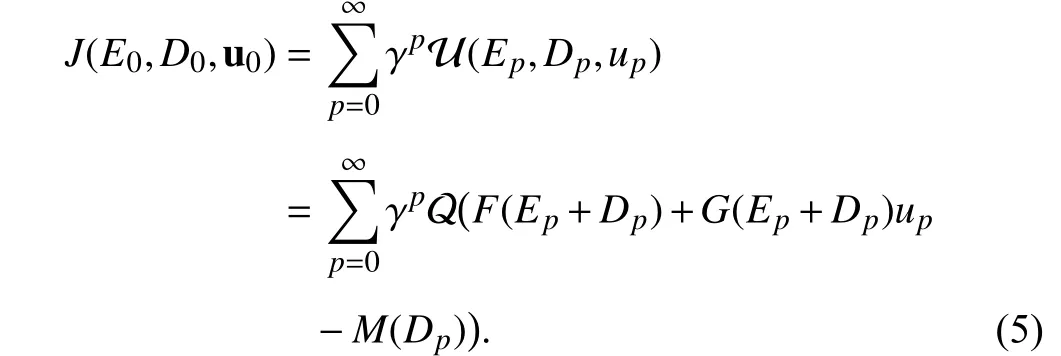
The adopted cost function (5) not only avoids computing the feedforward control input, but also eliminates the tracking error. The objective of this paper is to find a feedback control policy π(E,D), which both makes the dynamical system (1)track the reference trajectory and minimizes the cost function(5). According to (5), the state value function can be obtained as

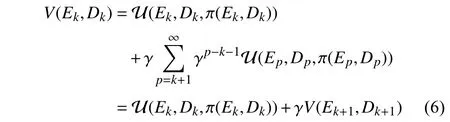
and its optimal value isV∗(Ek,Dk).

According to the Bellman’s principle of optimality, the optimal value function for tracking control problem satisfies

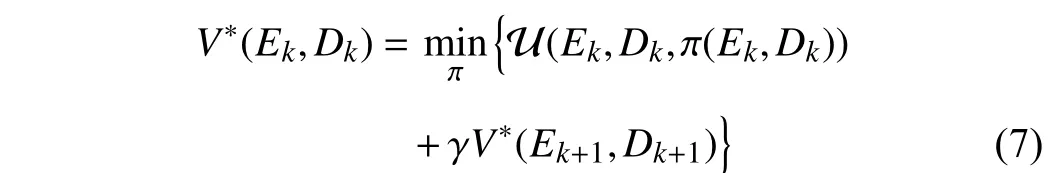
whereEk+1=F(Ek+Dk)+G(Ek+Dk)π(Ek,Dk)−M(Dk). The corresponding optimal control policy is computed by

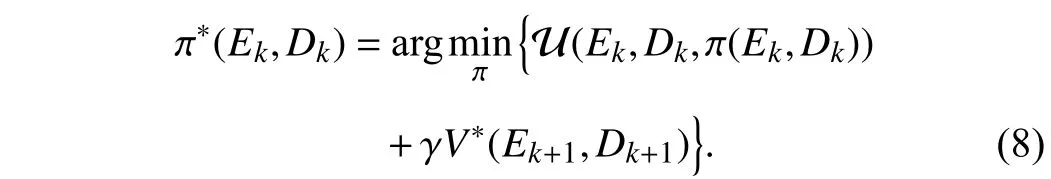
Therefore, the Hamiltonian function for tracking control can be obtained as

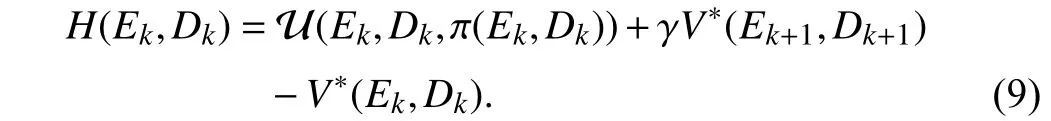
The optimal control policy π∗satisfies the first-order necessary condition for optimality, i.e.,=0 [42]. The gradient of(9) with respect toπis given as

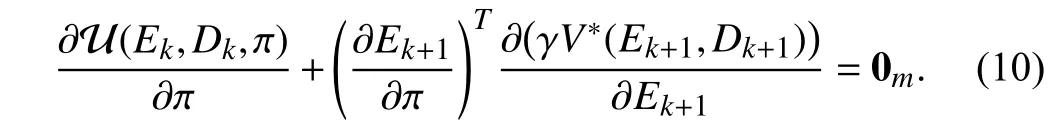
In general, the positive definite function Q is chosen as the following quadratic form:

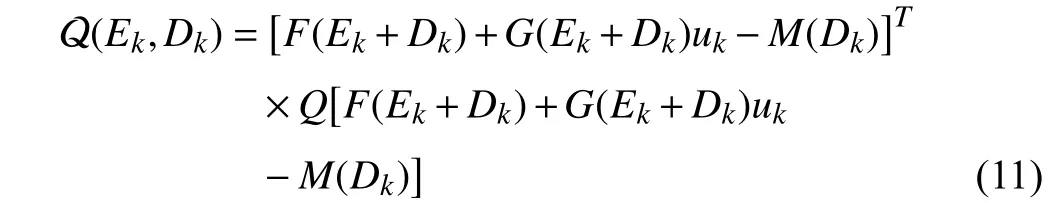
whereQ∈Rn×nis a positive definite matrix. Then, the expression of the optimal control policy can be obtained by solving (10) [42].

Since it is difficult or impossible to directly solve the Bellman equation (7), iterative adaptive critic methods are widely adopted to obtain its numerical solution. Here, the VIbased adaptive critic scheme for the tracking control problem is employed to approximate the optimal value functionV∗(Ek,Dk)formulated in (7). The VI-based adaptive critic algorithm starts from a positive semi-definite continuous value functionV(0)(Ek,Dk).UsingtheinitialvaluefunctionV(0)(Ek,Dk),theinitialcontrol policy iscomputed by

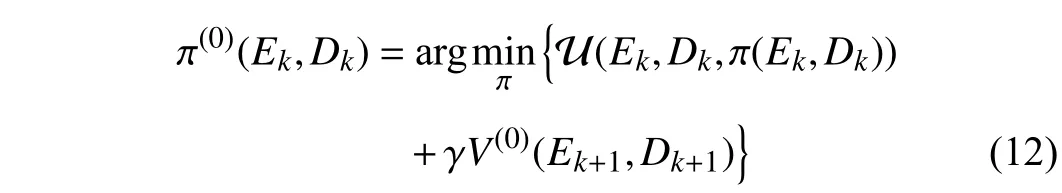
whereEk+1=F(Ek+Dk)+G(Ek+Dk)π(Ek,Dk)−M(Dk). For the iteration index ℓ ∈N+, the VI-based adaptive critic algorithm is implemented between the value function update

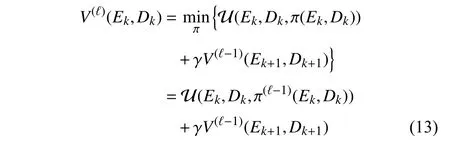
and the policy improvement

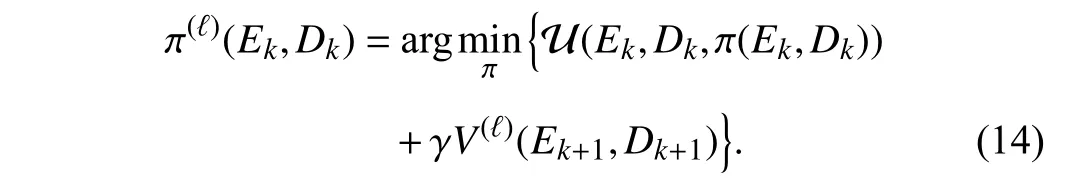
In the iteration learning process, two sequences, namely the iterative value function sequence {V(ℓ)} and the corresponding control policy sequence {π(ℓ)}, are obtained. The convergence and monotonicity of the undiscounted value function sequence have been investigated in [42]. Inspired by [42], the corresponding convergence and monotonicity properties of the discounted value function can be obtained.

Lemma 1 [42]:Let the value function and control policy sequences be tuned by (13) and (14), respectively. For anyEkandDk, the value function starts fromV(0)(·,·)=0.

1) The value function sequence {V(ℓ)(Ek,Dk)} is monotonically nondecreasing, i.e.,V(ℓ)(Ek,Dk)≤V(ℓ+1)(Ek,Dk),ℓ ∈N.

2) Suppose that there exists a constant κ ∈(0,∞) such that 0 ≤γV∗(Ek+1,Dk+1)≤κU(Ek,Dk,uk), whereEk+1=F(Ek+Dk)+G(Ek+Dk)uk−M(Dk). Then, the iterative value function approaches the optimal value function with the following manner:

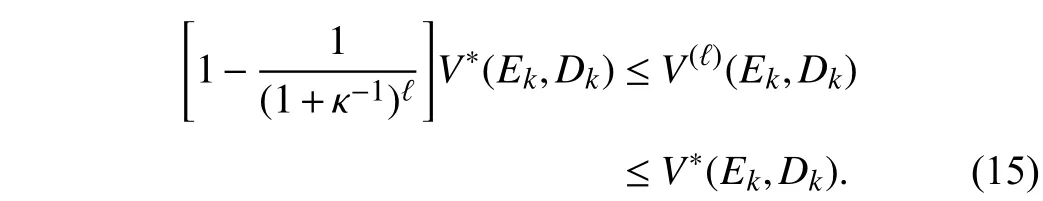
It can be guaranteed that the discounted value function and corresponding control policy sequences approximate the optimal value function and optimal control policy as the number of iterations increases, i.e.,limℓ→∞V(ℓ)(Ek,Dk)=V∗(Ek,Dk) and limℓ→∞π(ℓ)(Ek,Dk)=π∗(Ek,Dk). Note that the introduction of the discount factor will affect the stability of the optimal and iterative control policies. If the discount factor is chosen too small, the optimal control policy might be unstable. For the tracking control problem, the policy π∗(Ek,Dk)cannot make the controlled plant track the desired trajectory. It is meaningless to design various iterative methods to approximate the optimal control policy. On the other hand, for the regulation problem, the iterative value function is a Lyapunov function to judge the stability of the closed-loop systems [18]. However, for the tracking control problem, the iterative value function cannot be regarded as a Lyapunov function as the iterative value function does not only depend on the tracking errorE. Therefore, it is necessary to develop a novel stability analysis approach for tracking control problems.

III. NOVEL STABILITY ANALYSIS OF VI-BASED ADAPTIVE CRITIC DESIGNS

In this section, the stability of the tracking error system is discussed. It is guaranteed that the tracking error under the iterative control policy converges to zero as the number of time steps increases.

Theorem 1:Suppose that there exists a control sequenceu0for the system (1) and the desired trajectory (3) such thatEk→0 ask→∞. If the discount factor satisfies

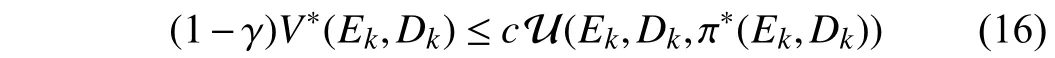
wherec∈(0,1) is a constant, then the tracking error under the optimal control π∗(Ek,Dk) converges to zero ask→∞.

Proof:According to (7) and (8), the Bellman equation can be rewritten as

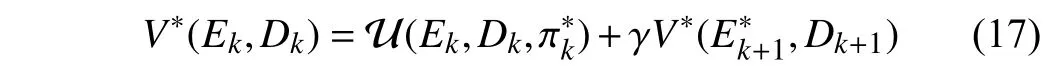
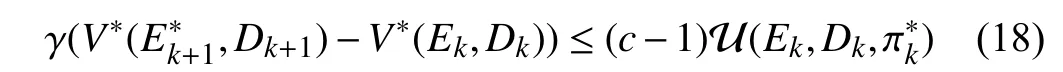
which is equivalent to

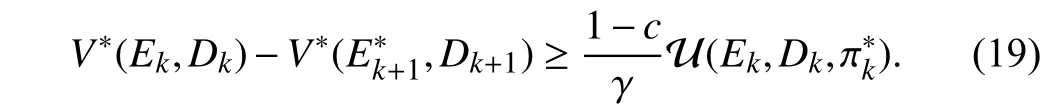
Applying (19) to the tracking errorsE0,E1, ...,ENand the corresponding reference pointsD0,D1, ...,DN, one has

Combining the inequalities in (20), we have

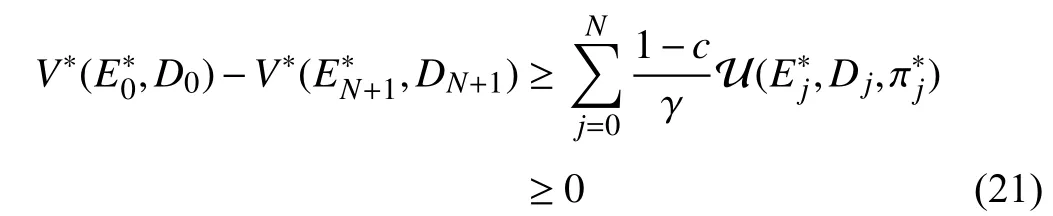
For the discounted iterative adaptive critic tracking control,the condition (16) is important. Otherwise, the stability of the optimal control policy cannot be guaranteed. Theorem 1 reveals the effect of the discount factor on the convergence of the tracking error. However, the optimal value function is unknown in advance. In what follows, a practical stability condition is provided to guarantee that the tracking error converges to zero under the iterative control policy.

Theorem 2:Let the value function with(·,·)=0 and the control policy be updated by (13) and (14), respectively. If the iterative value function satisfies

which implies, forj=1,2,...,N

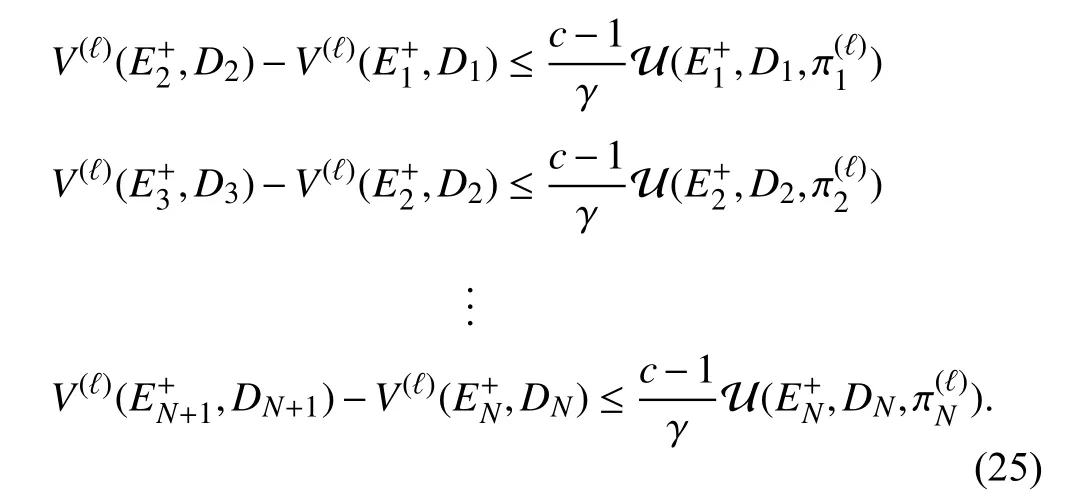
Combining (23) and (25), the following relationship can be obtained:

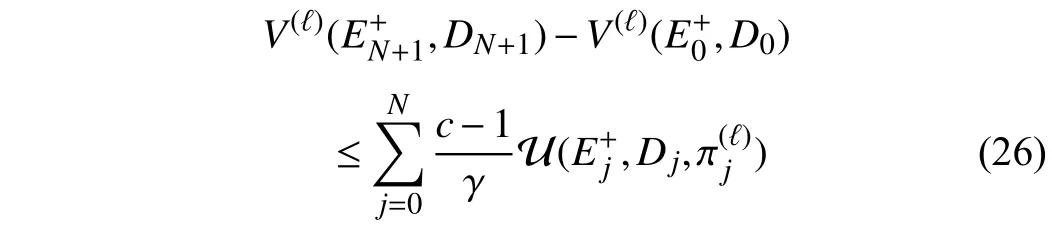
According to 2) in Lemma 1,V(ℓ+1)(Ek,Dk)−V(ℓ)(Ek,Dk)→0 as ℓ →∞. Therefore, the condition (22) in Theorem 2 can be satisfied in the iteration process. There must exist an iterative control policyin the control policy sequence {π(ℓ)}, which makesEk→0 ask→∞.

In general, for nonlinear systems, the value function update(13) cannot be solved exactly. Various fitting methods, such as neural networks, polynomial fitting and so forth, can be used to approximate the iterative value function of the nonlinear systems and many numerical methods can be applied to solve (14). Note that the inputs of the function approximator are the tracking error vectorEand the desired trajectoryD.Especially, for high dimensional nonlinear systems, the artificial neural network is applicable to approximate the iterative value function. Compared with the polynomial fitting method, the artificial neural network avoids manually designing each basis function. The introduction of the function approximator inevitably leads to the approximation error.

Define the approximation error at theℓth iteration as ε(ℓ)(Ek,Dk). According to the value function update equation(13), the approximate value function is obtained as

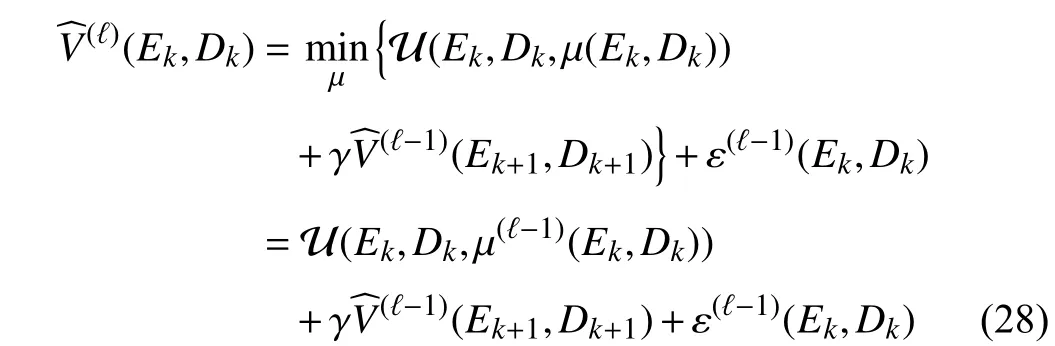
whereEk+1=F(Ek+Dk)+G(Ek+Dk)µ(Ek,Dk)−M(Dk) and the corresponding control policy µ (Ek,Dk) is computed by

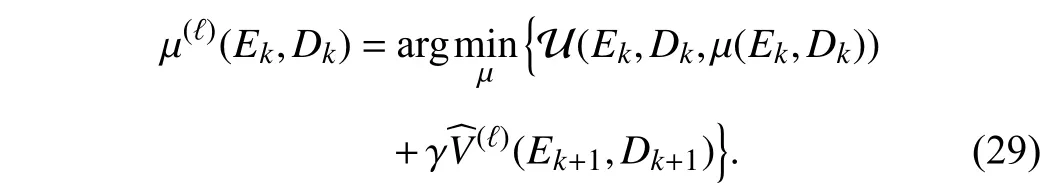
Note that the approximation error ε(ℓ−1)(Ek,Dk) is not the error between the approximate value function(ℓ)(Ek,Dk) and the exact value functionV(ℓ)(Ek,Dk). Next, considering the approximation error of the function approximator, we further discuss the stability of the closed-loop system using the control policy derived from the approximate value function.

Theorem 3:Let the iterative value function withV(0)(·,·)=0 be approximated by a smooth function approximator. The approximate value function and the corresponding control policy are updated by (28) and (29), respectively. If the approximatevaluefunction withtheapproximationerror≤αU(Ek,Dk,µ(ℓ)(Ek,Dk))isfiniteand satisfies where α ∈(0,1) andc∈(0,1−α) are constants, then the tracking error under the control policy µ(ℓ)(Ek,Dk) satisfiesEk→0ask→∞.

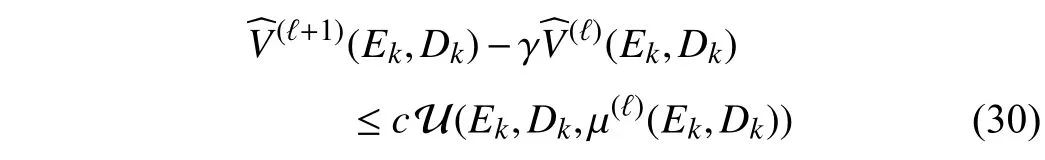
Proof:Forconvenience, in the sequel, µ(ℓ)(Ek,Dk) is written as.According to (28) and the condition(30),itleadsto

Evaluating (32) at the time stepsk=0,1,2,...,N, it results in

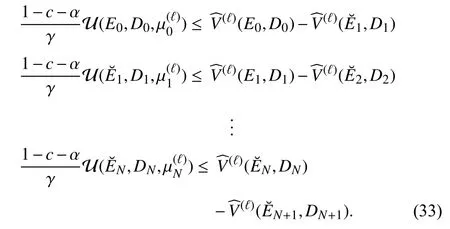
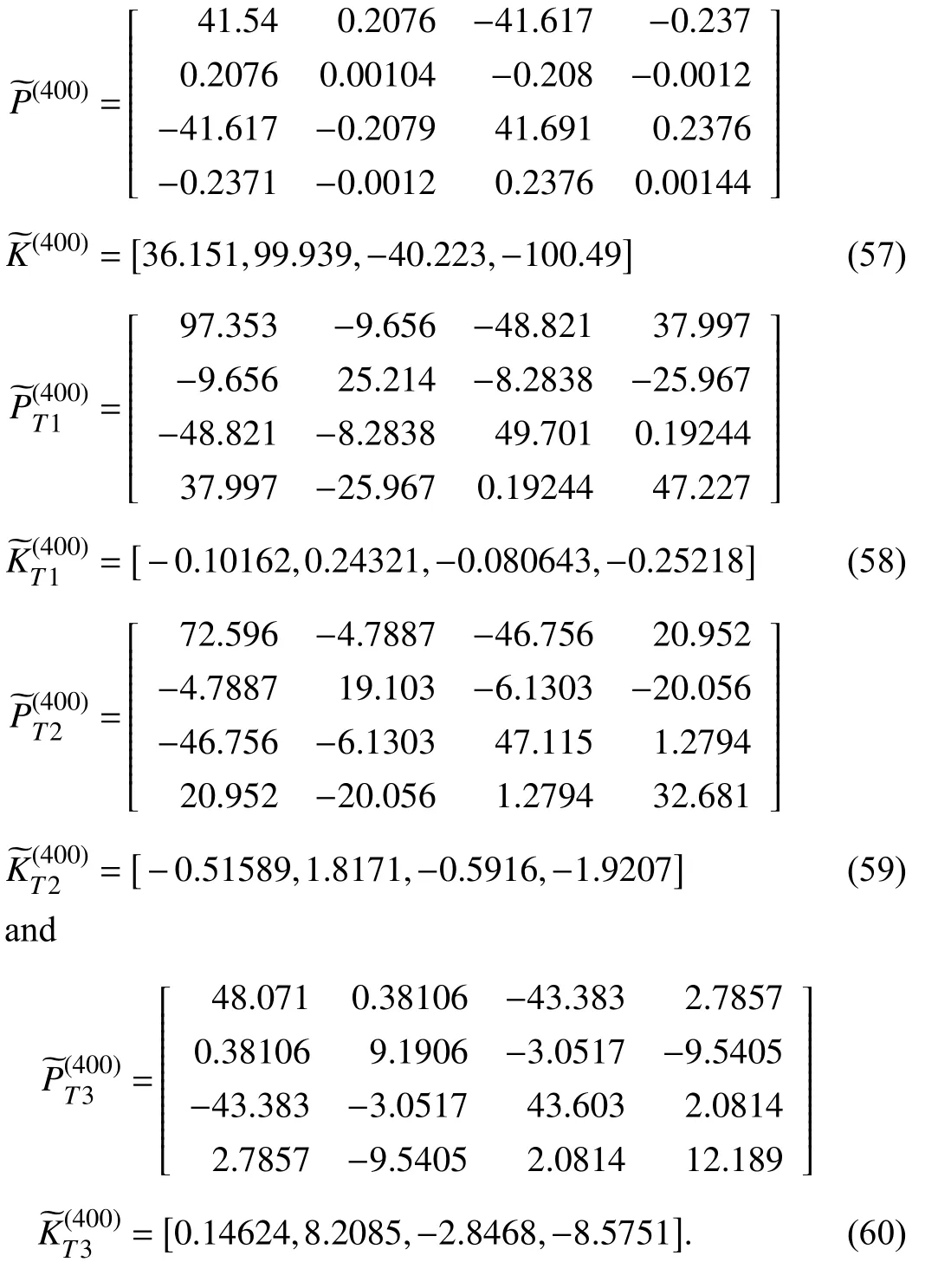
Combining the inequalities in (33), we obtain

IV. DISCOUNTED TRACKING CONTROL FOR THE SPECIAL CASE OF LINEAR SYSTEMS

In this section, the VI-based adaptive critic scheme for linear systems and the stability properties are investigated.Consider the following discrete-time linear systems given by

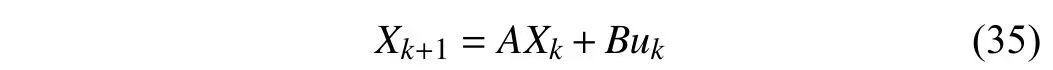
whereA∈Rn×nandB∈Rn×mare system matrices. Here, we assume that the reference trajectory satisfiesDk+1=ΓDk,where Γ ∈Rn×nis a constant matrix. This form is used because its analysis is convenient. According to the new cost function(5), for the linear system (35), a quadratic performance index with a positive definite weight matrixQis formulated as follows:

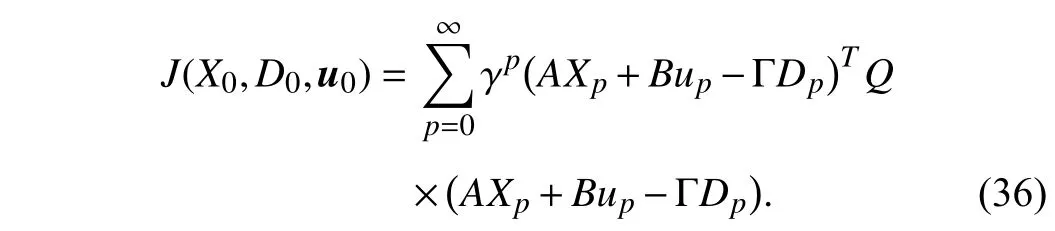
Combining the dynamical system (35) and the desired trajectoryDk, we can obtain an augmented system as

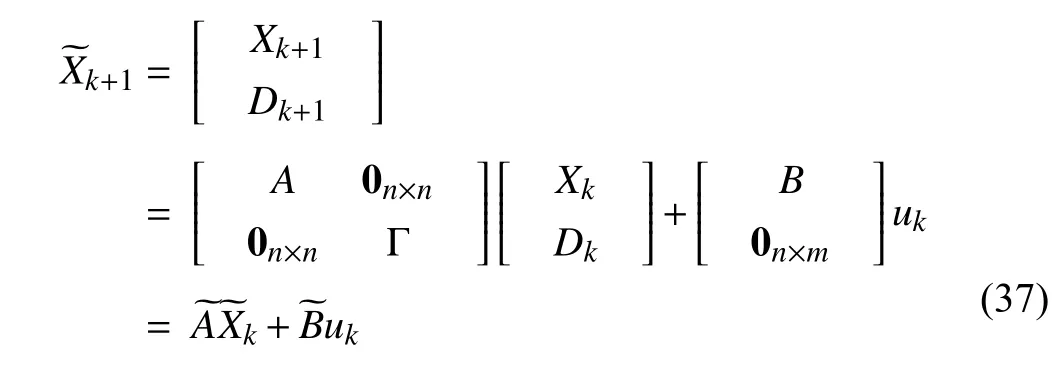
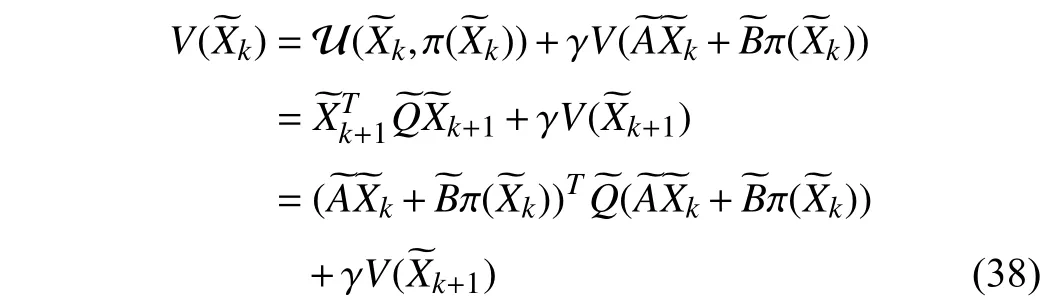
where the new weight matrixsatisfies

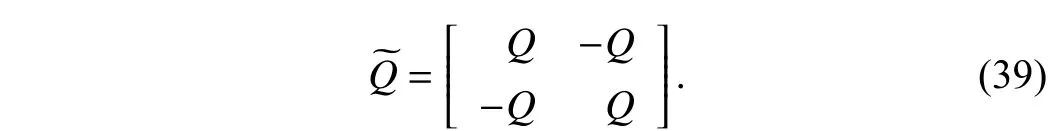
As mentioned in [15], [16], [39], the value function can be regarded as the quadratic form in the state, i.e.,V()=for some kernel matrix. Then, the Bellman equation of linear quadratic tracking is obtained by

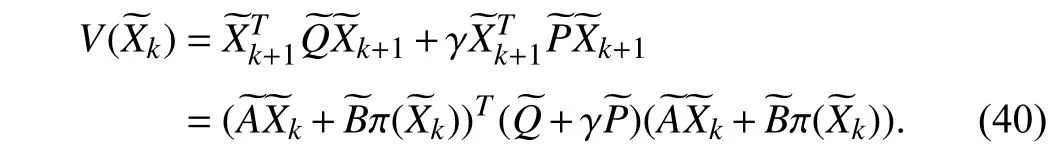
The Hamiltonian function of linear quadratic tracking control is defined as

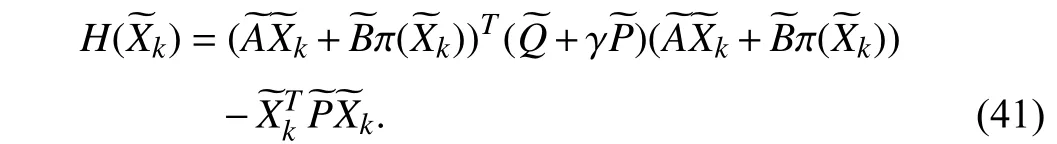
Considering the state feedback policy π ()=−and the equation (40), it results in

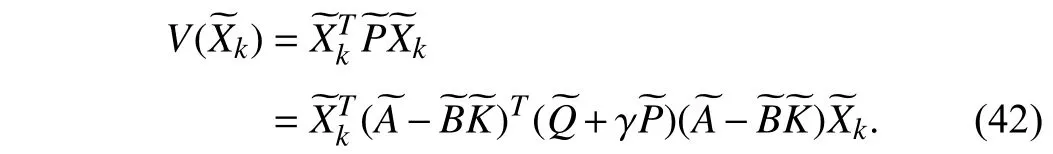
Therefore, the linear quadratic tracking problem can be solved by using the following equation:

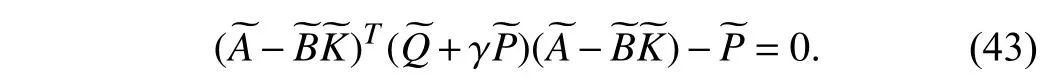
Considering the Hamiltonian function (41), a necessary condition for optimality is the stationarity condition=0[15 ], [16]. The optimal control policy is computed by

and

Theorem 4:Let the kernel matrix and the state feedback gain be iteratively updated by (45) and (46), respectively. If the iterative kernel matrix and state feedback gain satisfy

which implies

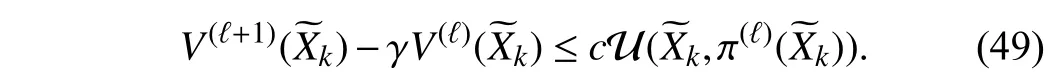
According to Theorem 2, we can obtainU(,π(ℓ)())→0 ask→∞,whichshows thatthetracking errorunder the iterativecontrol policy π(ℓ)()approacheszero ask→∞. ■

For linear systems, if the system matricesAandBare known, it is not necessary to use the function approximator to estimate the iterative value function. According to the iterative algorithm (45) and (46), there is no approximation error derived from the approximate value function in the iteration procedure.

V. SIMULATION STUDIES

In this section, two numerical simulations with physical background are conducted to verify the effectiveness of the discounted adaptive critic designs. Compared with the cost function (4) proposed by the traditional studies, the adopted performance index can eliminate the tracking error.

A. Example 1

As shown in Fig. 1, the spring-mass-damper system is used to validate the present results and compare the performance between the present and the traditional adaptive critic tracking control approaches. LetM,s, anddbe the mass of the object,the stiffness constant of the spring, and the damping, respectively. The system dynamics is given as

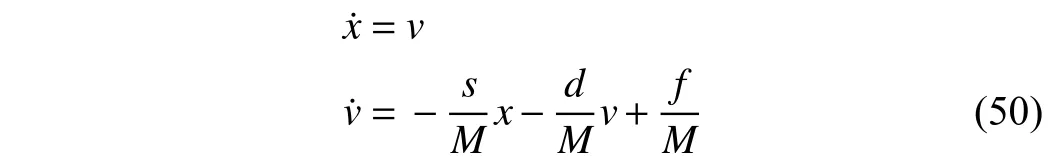
wherexdenotes the position,vstands for the velocity, andfis theforce appliedtotheobject. Letthesystemstate vectorbeX=[x,v]T∈R2andthe controlinputbeu=f∈R. The continuous-time system dynamics (50) is discretized using the Euler method with sampling interval ∆t=0.01 s. Then, the discrete-time state space equation is obtained as

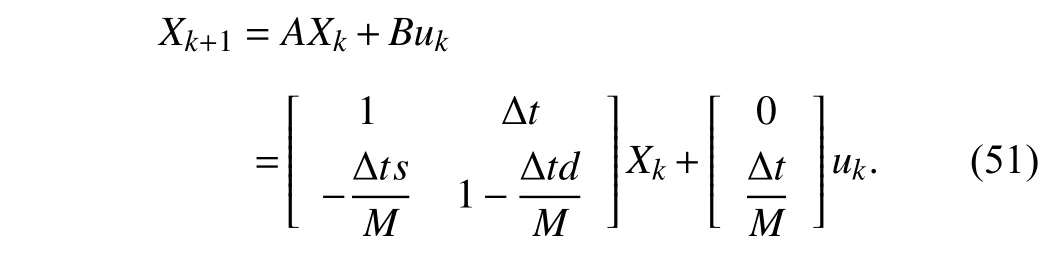
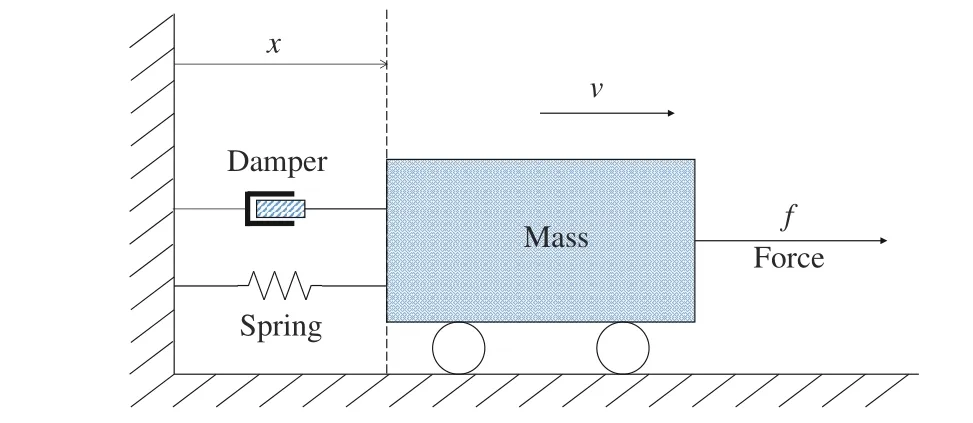
Fig. 1. Diagrammatic sketch of the spring-mass-damper system.

In this example, the practical parameters are selected asM=1 kg,s=5 N/m, andd=0.5 Ns/m. The reference trajectory is defined as

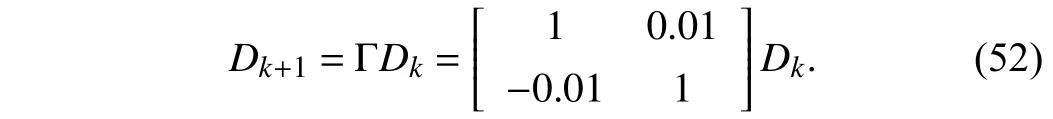
Combining the original system (51) and the reference trajectory (52), the augmented system is formulated as

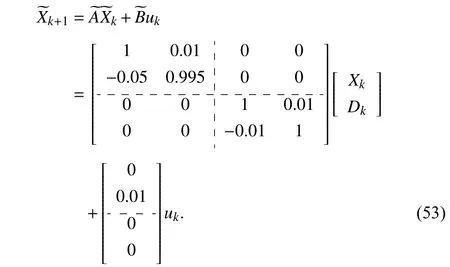
The iterative kernel matrix with(0)=04×4and the state feedback gain are updated by (45) and (46), respectively,whereQ=I2and the discount factor is chosen as γ =0.98. On the other hand, considering the following traditional cost function:

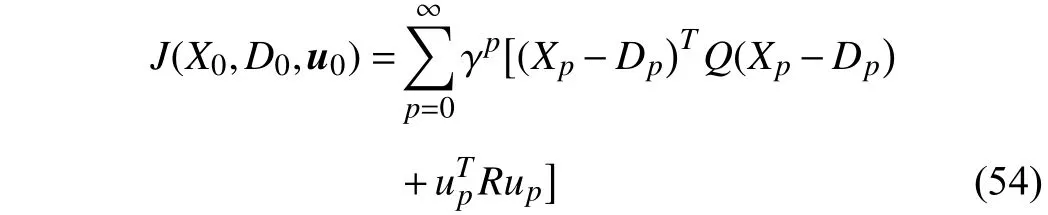
the corresponding VI-based adaptive critic control algorithm for system (53) is implemented between

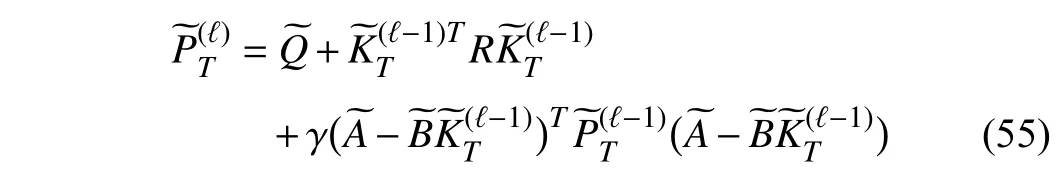
and

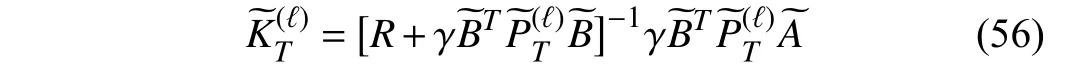
whereR∈Rm×mis a positive definite matrix. As defined in(54), the objective of the cost function is to minimize both the tracking error and the control input. The role of the cost function (54) is to balance the minimizations of the tracking error and the control input according to the selection of the matricesQandR. To compare the tracking performance under different cost functions, we carry out the new VI-based adaptive critic algorithm and the traditional approach for 400 iterations. Three traditional cost functions with different weight matricesQiandRi,i=1,2,3 are selected to implement the algorithms (55) and (56), whereQ1,2,3=I2andR1,2,3=1,0.1,0.01. After 400 iteration steps, the obtained corresponding optimal kernel matrices and state feedback gains are given as follows:

Let the initial system state and reference point beX0=[0.1,0.14]TandD0=[−0.3,0.3]T. Then, the obtained state feedback gains are applied to generate the control inputs of the controlled plant (53). The system state and tracking error trajectories under different weight matrices are shown in Figs. 2 and 3, respectively. It can be observed that smallerRleads to smaller tracking error. The weight matricesQandRreveal the importance of the minimizations of the tracking error and the control input. The tracking performance of the traditional cost function with smallerRis similar to that of the new tracking control approach. From (56), the matrixRcannot be a zero matrix. Otherwise, there might exist no inverse of the matrixR+. The corresponding control input curves are plotted in Fig. 4.

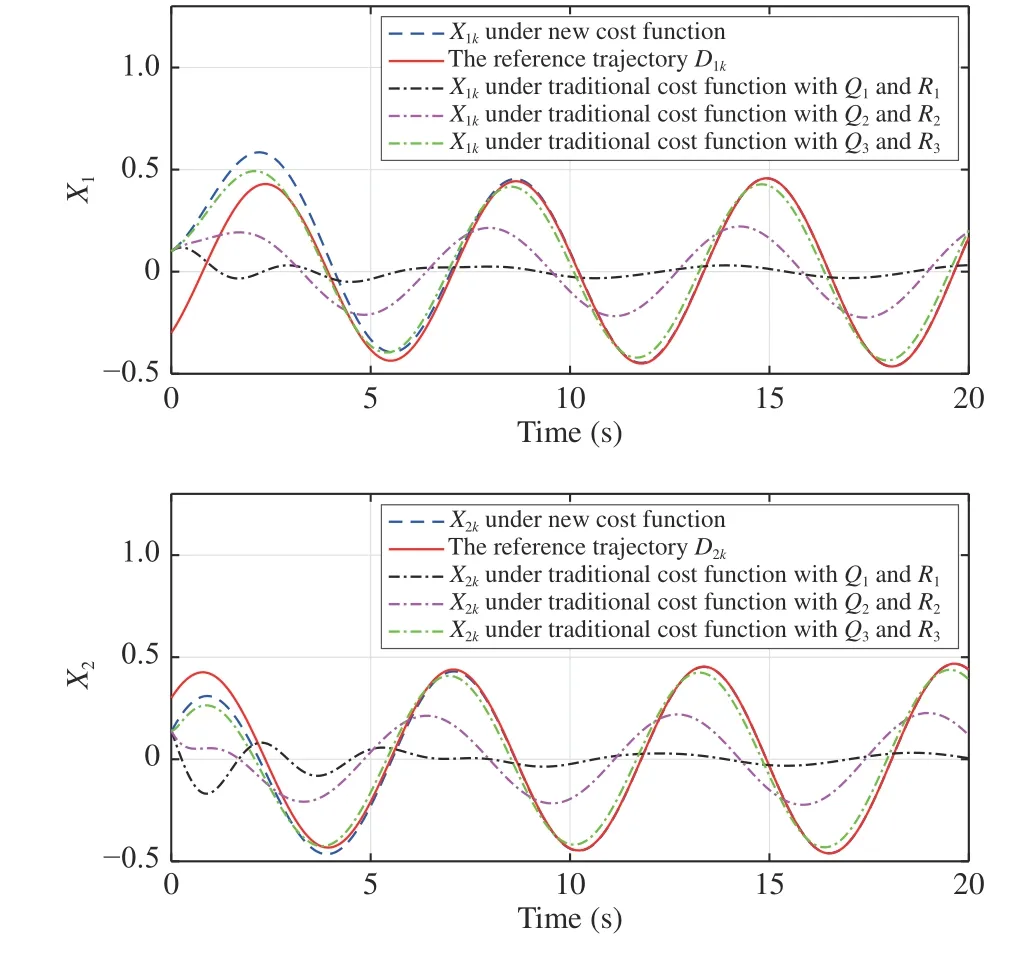
Fig. 2. The reference trajectory and system state curves under different cost functions (Example 1).

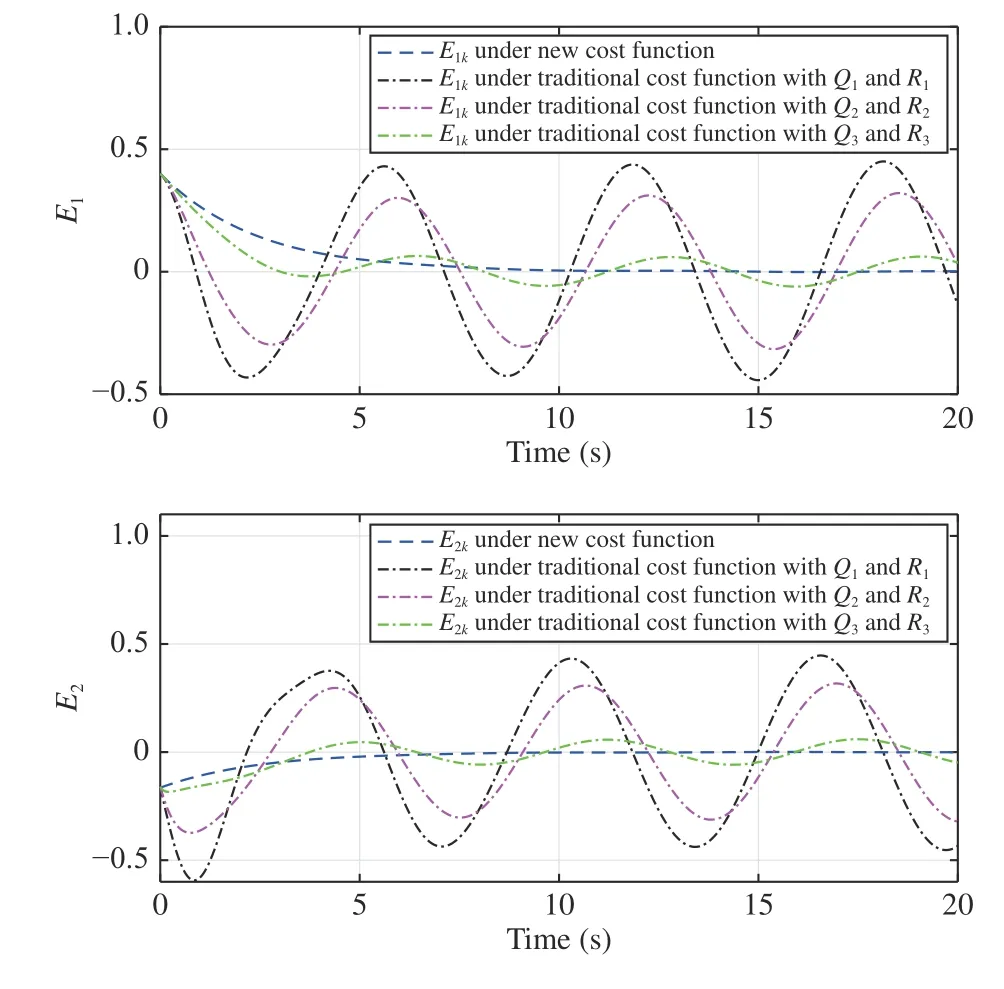
Fig. 3. The tracking error curves under different cost functions (Example 1).

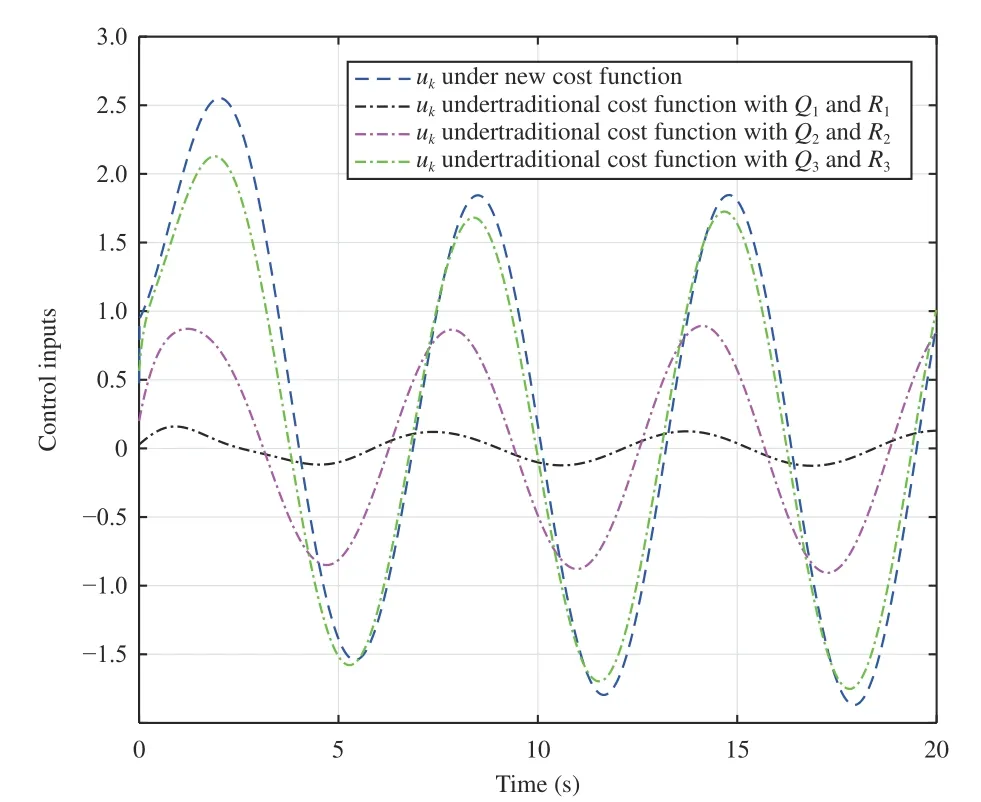
Fig. 4. The control input curves under different cost functions (Example 1).

B. Example 2

Consider the single link robot arm given in [47]. LetM,g,L, J andfrbe the mass of the payload, acceleration of gravity, length of the arm, moment of inertia and viscous friction, respectively. The system dynamics is formulated as

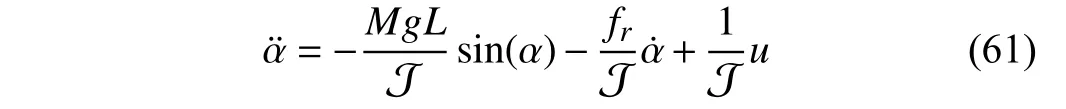
whereαandudenote the angle position of robot arm and controlinput, respectively.LetthesystemstatevectorbeX=[α,α˙]T∈R2. SimilarlytoExample 1,the singlelink robot arm dynamics is discretized using the Euler method with sampling interval ∆t=0.05 s. Then, the discrete-time state space equation of (61) is obtained as

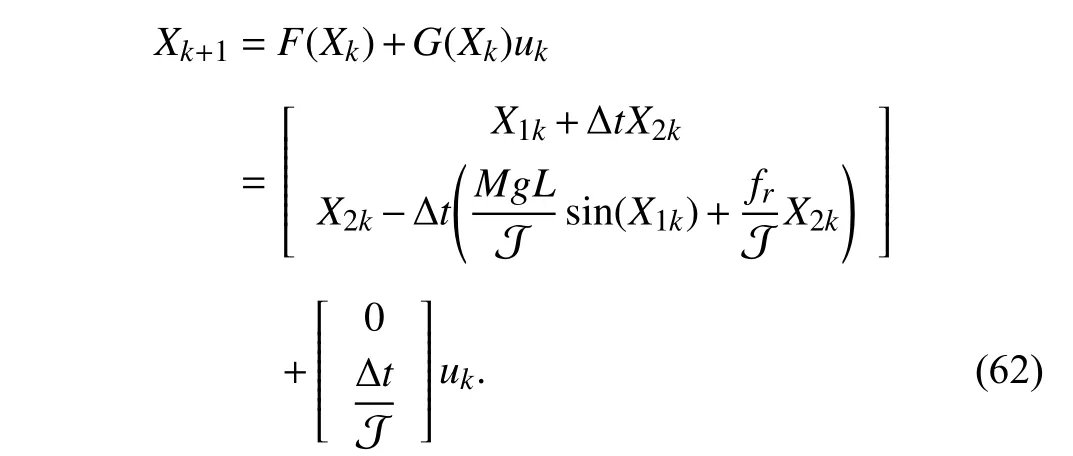
Inthisexample,thepractical parametersaresetasM=1kg,g=9.8m/s2,L=1m ,J =5 kg·m2andfr=2.The desired trajectory is defined as

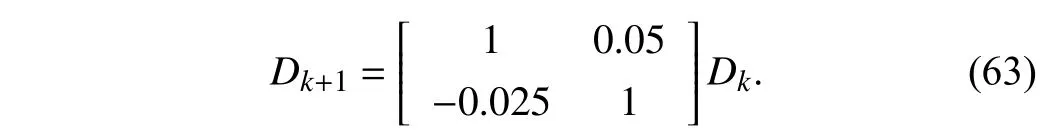
The cost function (5) is set as the quadratic form, whereQandγare selected asQ=I2and γ=0.97, respectively. In this example, sinceEkandDkare the independent variables of the value function, the function approximator of the iterative value function is selected as the following form:

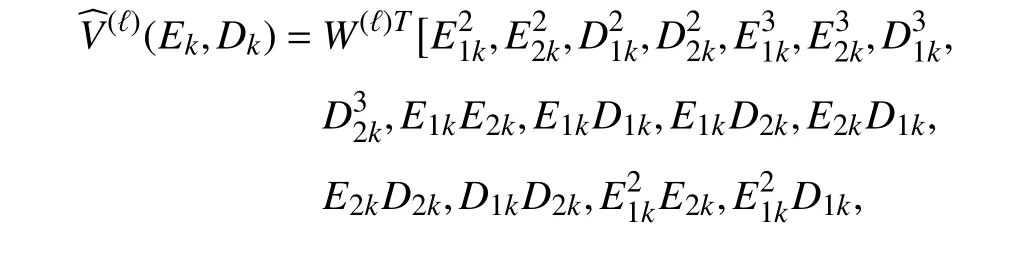
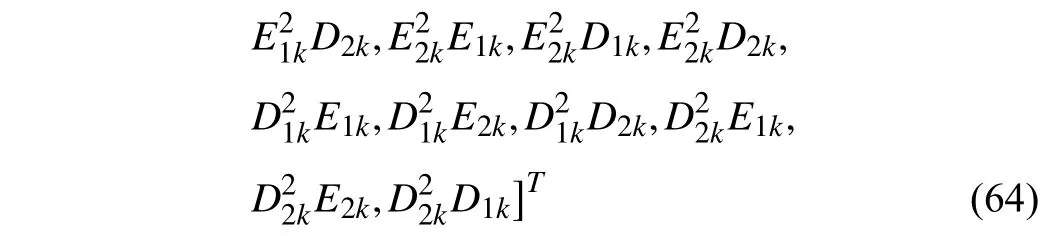
whereW(ℓ)∈R26is the parameter vector. In the iteration process, 300 random samples in the region Ω={(E∈R2,D∈R2):−1 ≤E1≤1,−1 ≤E2≤1,−1 ≤D1≤1,−1 ≤D2≤1}are chosen to learn the iterative value functionV(ℓ)(E,D) for 200 iteration steps. The value function is initialized as zero. In the iteration process, considering the first-order necessary condition for optimality, the iterative control policy can be computed by the following equation:

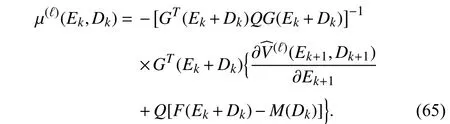
Note that the unknown control input µ(ℓ)(Ek,Dk) exists on both sides of (65). Therefore, at each iteration step,µ(ℓ)(Ek,Dk)is iteratively obtained by using the successive approximation approach. After the iterative learning process,the parameter vector is obtained as follows:

Next, we compare the tracking performance of the new and the traditional methods. The traditional cost function is also selected as the quadratic form. Three traditional cost functions withQ1,2,3=I2andR1,2,3=0.1,0.01,0.001 are selected. The initial state and initial reference point are set asX0=[−0.32,0.12]TandD0=[0.12,−0.23]T, respectively. The obtained parameter vectors derived from the present and the traditional adaptive critic methods are employed to generate the near optimal control policy. The controlled plant state trajectories using these near optimal control policies are shown in Fig. 5. The corresponding tracking error and control input curves are plotted in Figs. 6 and 7, respectively. From Figs. 6 and 7, it is observed that both the tracking error and the control input derived from the traditional approach are minimized. However, it is not necessary to minimize the control input by deteriorating the tracking performance for tracking control.

VI. CONCLUSIONS

In this paper, for the tracking control problem, the stability of the discounted VI-based adaptive critic method with a new performance index is investigated. Based on the new performance index, the iterative formulation for the special case of linear systems is given. Some stability conditions are provided to guarantee that the tracking error approaches zero as the number of time steps increases. Moreover, the effect of the presence of the approximation errors of the value function is discussed. Two numerical simulations are performed to compare the tracking performance of the iterative adaptive critic designs under different performance index functions.

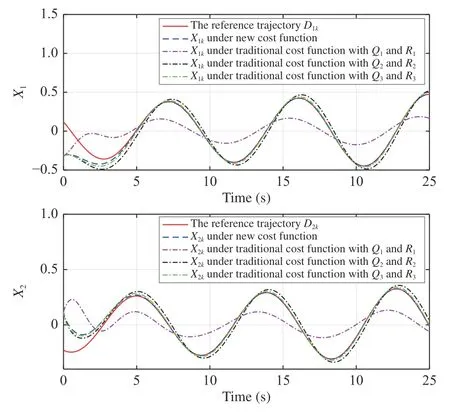
Fig. 5. The reference trajectory and system state curves under different cost functions (Example 2).

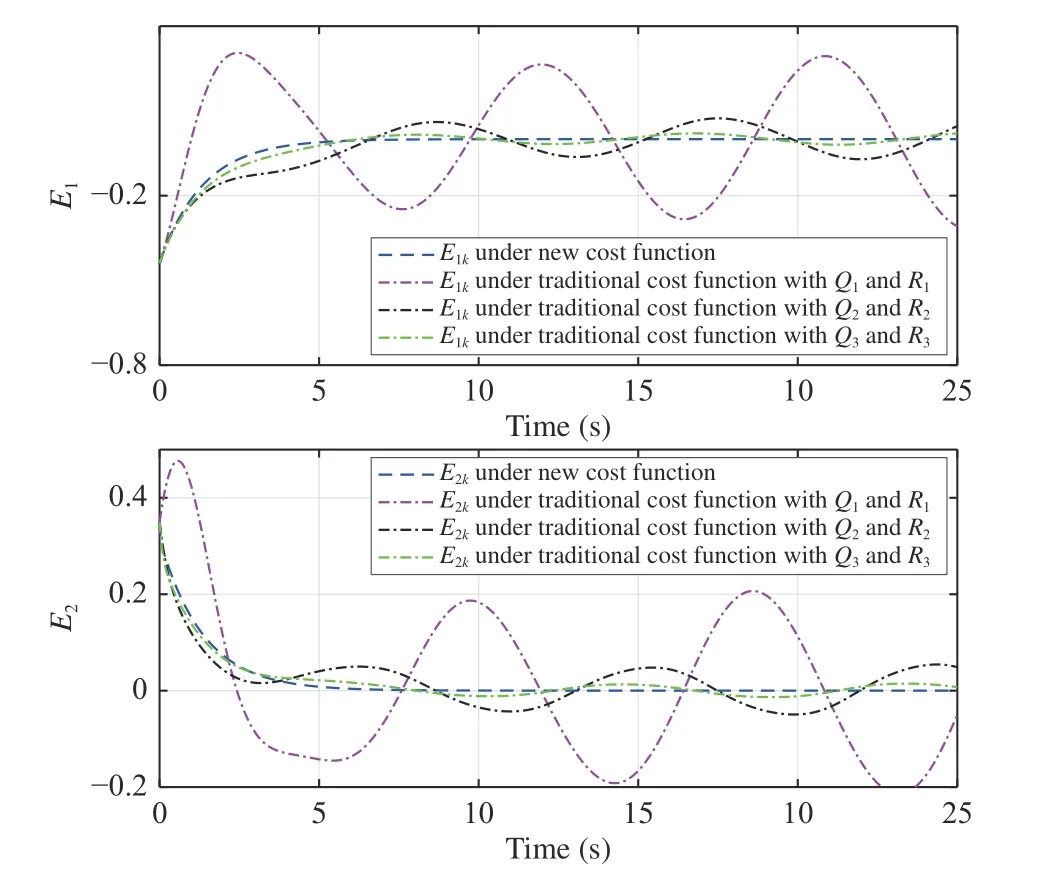
Fig. 6. The tracking error curves under different cost functions (Example 2).

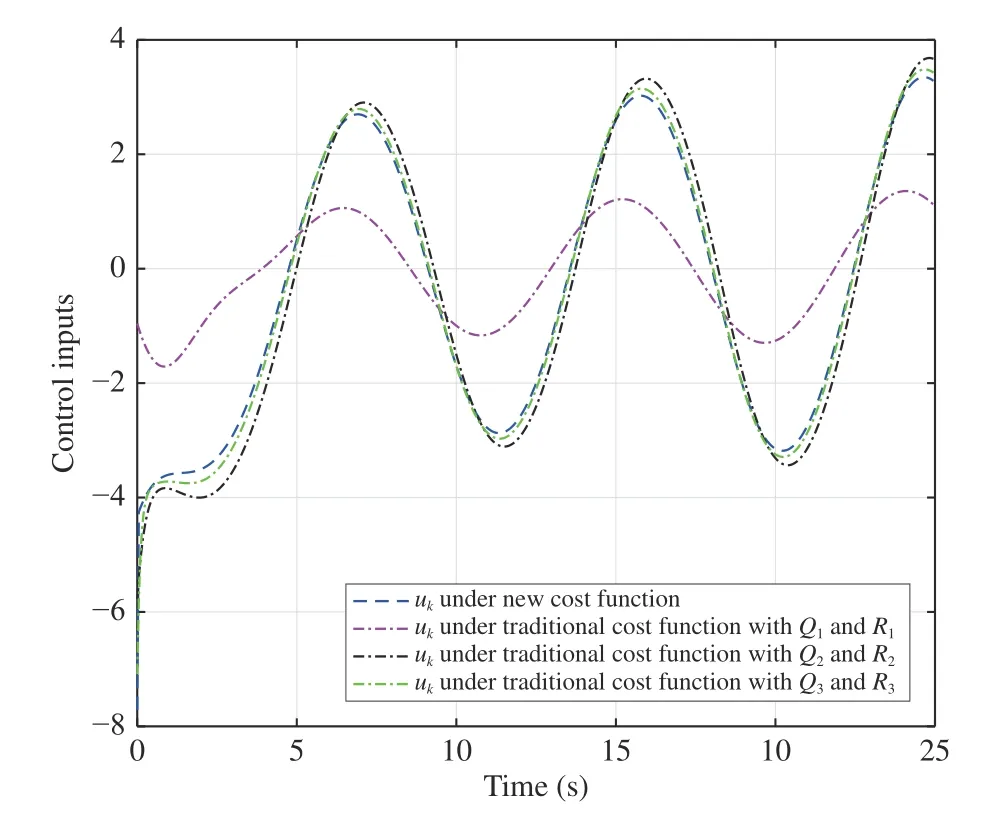
Fig. 7. The control input curves under different cost functions (Example 2).

It is also interesting to further extend the present tracking control method to the nonaffine systems, data-based tracking control, output tracking control, various practical applications and so forth. The developed tracking control method will be more advanced in the future work of online adaptive critic designs for some practical complex systems with noises.