基于Logistic模型研究花生根长与干物质积累的关系
2022-07-18梁仕军化存才
梁仕军,化存才
(云南师范大学 数学学院,云南 昆明 650000)
花生是世界上重要的粮食、饲料作物和油料作物之一.中国是花生生产、消费和出口贸易最大的国家.因此,花生的增产不仅可以保证我国的油料安全,而且也可以带动我国的经济发展.
花生是具有无限开花结实习性的草本作物,其开花期和结实期很长,生育期也较长.一般早熟品种100~130 d,中熟品种135~150 d,晚熟品种 150 d 以上.花生的生长发育时期分为:破土期(种子发芽出苗期),幼苗期,下针期(开花下针期),结荚期,饱果期和成熟期.草本植物的根系,无论是作物还是非作物,都是由粗根和细根组成的,细根是根系中吸收水分最活跃的部分.植物根系的生长发育与其开花结果产量、抗旱等有着重要的关系,文献[1]作了如下事实描述:植物根系的大小和长短是获取水分、无机盐等土壤资源的关键特征.尤其是,在干旱条件下,植物根据有效土壤水分分布而生根的能力,极大地提高了植物在干旱条件下的产量.对于花生而言,根系的长度将影响花生干物质的积累以及产量,花生的根长与产量呈正相关.
Logistic模型是描述具有S型动态发展曲线的一个经典的微分方程,有着比较广的应用范围.例如,王明斋等[2]将Logistic微分方程模型应用到结核病疫情预警中,分析得出了3个疫情防控结点:渐增期、快增期和缓增期.张林等[3]在研究降低UV-B辐射对烤烟株高影响的问题时建立了如下非自治的Logistic模型:

其中,H表示烤烟的株高,Hm表示烤烟的最大株高,r(t)表示与时间有关的增长率.
又如,刘春等[4]基于能量模型建立了水稻生长的如下Logistic型二维微分方程模型:

其中,T表示气温,Tu表示最适气温,u表示水稻生物量.
最近,李文斌[5]在考虑声频控制会影响水稻生长的数学问题时,基于Logistic建立了决定水稻产量的水稻分蘖期生长的微分方程模型.
至今,没有见到文献基于Logistic微分方程模型去研究花生生长发育中的相关规律.为此,本文的主要目的是研究花生根长与干物质的积累之间的关系.将基于花生生长发育的基本事实和Logistic模型建立二维微分方程组模型,并进行数值模拟分析和应用阐释.
1 二维微分方程组模型的建立与分析
1.1 模型的建立
根据参考文献[1],可提取花生生长发育过程中的以下基本事实:
F1)随着花生的生长发育期的推进,花生的根系的活力逐渐下降,其中在苗期时根系的活力最高;
F2)随着花生的生长发育期的推进,花生的根长不断增加;
除了安特莱夫的《默》对鲁迅的《药》的创作有明显的影响之外,安特莱夫的另一篇小说《齿痛》也对《药》的主题产生了很大的影响。《齿痛》描写的是耶稣在各各他被钉上十字架的那一天,各各他附近有个商人患着齿痛。他也和《药》里的华老栓一样,只关注自己的齿痛,而对耶稣的死毫不理解,并表现出极度的冷漠。
F3)花生苗期根长与产量呈显著正相关,开花下针期与饱果成熟期根长与产量呈极显著正相关.
基于以上3个事实,我们做出以下合理假设:
H1)花生根部的生长增长速率先增后减,符合二次函数模型;
H2)花生的干物质积累越大,花生根长的增长速率越小;
H3)干物质的积累速度随花生根的长度的增加而增加;
H4)干物质的积累速度随干物质的积累量的增加而减慢;
H5)在不考虑根长影响因素时,花生干物质的积累量的最大值设为K.
(1)
其中,α,a,b,c>0,且为常数.
1.2 参数估计
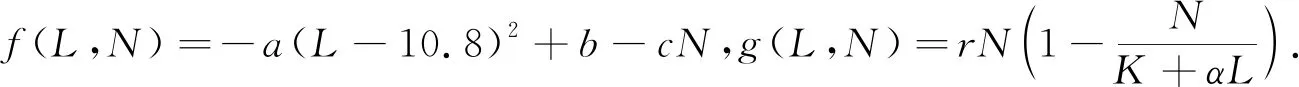
由f(L,N)=0,g(L,N)=0得正平衡点为(L0,K+αL0),其中L0为根的待定长度.
因为花生在播种后,生长过程为首先胚萌发,接着胚芽形成幼芽,然后胚根才形成幼根,所以若取(0,0.8)为花生的生长发育的起始点,则此时花生的根长为0,而干物质的积累量0.8为种子的质量,且根的增长速率不为0,取增长速率为 0.057 89,即:
-116.64a+b-0.8c=0.057 89.
(2)
正平衡点(L0,K+αL0)为花生生长发育过程的终点,此时花生的根生长速率为0,根的长度记作L0,所以
-a(L0-10.8)2+b-c(K+αL0)=0.
(3)
取定L0=20.7,K=60.8,则方程(3)可变形为
84.64a-b+(60.8+20α)c=0.
(4)
在苗期时,根据参考文献[1]的相关数据,假设花生的根长度为10.8,干物质的积累量为8.7,此时的根增长速率达到最大,最大值为:
b-8.7c=0.36.
(5)
如取α=0.5,则联立方程(2)~(5),得:
a=0.002 7,b=0.374 1,c=0.001 6,K=60.8,r=0.059,α=0.5.
1.3 平衡点的稳定性分析
微分方程组模型(1)的雅可比矩阵为:
在参数估计下的微分方程组模型(1)变为:
(6)
平衡点(L0,K+αL0)=(20.7,71.15)处的雅可比矩阵为

记:p=-trA=0.112 46>0,q=detA≈0.003 2>0,Δ=p2-4q=-0.000 15<0.
因为p>0,q>0,Δ<0,所以平衡点(L0,K+αL0)是渐近稳定的焦点,这说明,花生的根长和干物质的积累量最终在稳定平衡点附近波动.
1.4 数值模拟
微分方程组模型(6)是一个非线性的二维微分方程组,无法求出其精确解,因此通过Matlab编程数值模拟画出解析式的图像和相图.

图1 花生根长与时间的关系 图2 花生干物质积累量与时间的关系 图3 花生根长与干物质积累量的关系相图
由图1、图2和图3可得以下结论:
i) 根长增长的拐点在苗期,干物质积累的拐点在开花下针期;
ii) 当根长为 10.8 cm 时,花生根长的增长速率为最大;
iii) 花生的根长的增长呈“S”型生长曲线,先慢后快,最后趋近于最大值;根长的增长主要集中在苗期和开花下针期;
iv) 花生的根长在 140 d 时达到稳定,此时根长为 20.7 cm;
v) 在加入花生根长的影响后,花生的干物质积累量增加,其最大增长速率变大.这也许是由于翻耕深度更深、土壤更加肥沃、水分阳光更适宜等因素使得根系生长更长,因此花生的产量会增加.
由花生根长与干物质积累量关系的L-N相图3,还可得:
1) 花生干物质的积累与根长正相关;
2) 图像下凸,并且倾斜程度越来越陡,这说明前期干物质积累速率低于花生根长的增长速率.
2 结语
基于花生生长发育的基本事实和Logistic模型,建立了花生根长与其干物质积累量关系的二维微分方程组模型(1),在进行了参数估计后,得到二维微分方程组模型(6),其正平衡点是稳定的焦点.
对二维微分方程组模型(6)的数值模拟结果表明,花生的根越长,花生干物质积累越多,呈正相关.结合花生生长的实际过程,可以作出如下合理的阐释:在花生的破土期以及苗期主要是生根,干物质积累较少;到了下针期,根的增长减慢,但是干物质积累明显增加,此时主要体现在茎和叶的生长;到了结荚期,和饱果成熟期,根的增长最缓慢,此时主要是荚果的发育和成熟,因此干物质积累很快.
