非线性成本下混合三寡头博弈的复杂动态性研究
2022-07-18陈诗宇刘星雨
王 静, 陈诗宇, 沈 佳, 刘星雨
(辽宁师范大学 数学学院,辽宁 大连 116029)
寡头垄断是现实经济运行中常见的市场结构,一些关系国计民生命脉的行业,大都是几家企业提供了市场中的绝大多数产品.在寡头垄断市场模式里,每个寡头的决策都不是孤立的,他们之间相互依存、相互影响,不但要考虑消费者的各种行为,而且要顾及竞争者的反应,并根据对手的策略不断修正自身的决策.因此,对寡头行为多样性和市场复杂性的研究具有重要的实际指导意义,众多研究者对寡头垄断市场这一领域展开了研究.
文献中关于双寡头博弈的复杂动态行为的研究成果极为丰富,如Cournot竞争[1]、Bertrand竞争[2]、Stackelberg竞争[3]、Cournot-Bertrand竞争[4].与双寡头博弈模型相比,文献对2个以上寡头企业竞争的研究较少.在实践中,这种博弈更接近经济现实,在寡头理论中应用广泛.然而,分析这种博弈的动态行为是一项复杂的工作.因此,早期的研究多是考虑使用相同预期原则的三寡头Cournot博弈.例如,Puu[5]在模型中考虑了3个使用静态预期的竞争者;Tu和Wang[6]假设3个竞争者采用有界理性期望;Alnowibet等人[7]考虑了3个使用适应性调节的竞争者,并且假设需求函数具有对数凹性.
近年来,研究者开始考虑采用不同预期的Cournot三寡头博弈模型.Elabbasy等人[8]研究了具有线性需求函数的异质竞争者的三寡头模型的动力学行为,3个竞争者分别采用有限理性预期、适应性预期和静态预期.随后,Elabbasy等人[9]进一步研究了具有非线性需求函数的异质竞争者的三寡头博弈模型.而Askar 和Alshamrani[10]讨论了4种三寡头模型:基于合作博弈的Cournot三寡头、有限理性的Bertrand三寡头、有限理性的Cournot三寡头、Puu三寡头模型.
然而,上述文献中的结果依赖于所有企业都是私人的且以利润最大化作为企业目标.这些研究不适用于日益流行的混合寡头博弈,即国有企业与私人企业进行竞争.关于混合寡头博弈的分析可以追溯到Merrill和Schneider[11].在大多数国家,国有企业对其市场竞争对手具有重大影响,如航空、钢铁、保险、医院和银行业等.
本文考虑国有企业与私人企业混合竞争的三寡头模型,并且假设产品的成本函数是非线性的.结合混沌理论,通过对边界均衡点和纳什均衡点的稳定性分析和数值模拟,研究混合竞争行为的复杂动态性,从而更好地解释寡头垄断市场中厂商的决策行为.
1 模型构建
假设市场上有3家企业生产类似的产品, 这3家企业分别为1家国有企业和2家私人企业.国有企业的目标为社会福利最大化(消费者剩余加企业利润),而私人企业的目标是利润最大化.现以q0,p0表示国有企业产品的产量和价格,qi和pi(i=1,2)分别表示私人企业i的产量和价格.设市场的逆需求函数为
(1)
其中:a(a>0)为市场对该产品的最大需求量,d为产品的差异系数.由(1)式可以得到市场的直接需求函数:
(2)
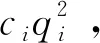
(3)
为简化分析,我们假设2家私人企业的单位生产成本相同,即c1=c2, 则参与竞争的两家私企的净利润为
(4)
将(4)式代入(3)式并注意到(1)式, 最终得
(5)
2 均衡点的稳定性
2.1 系统均衡点
对(5)中各式分别关于q0,q1,q2求偏导, 可得3家企业的边际利润表达式:
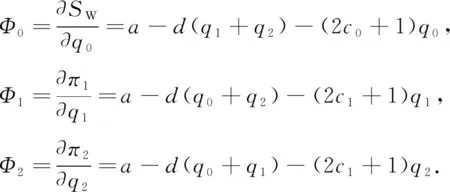
根据利润最大化条件, 令Φ0=0,Φ1=0,Φ2=0, 即可解得
(6)
在实际的市场竞争中, 不同企业间的博弈是一个动态过程, 企业通常会根据当前市场上的产量反馈信息对下一阶段的产量进行修正.本文假设国有企业和私人企业采用不同的产量预期,其中国有企业采用有界理性预期调整产量, 而2家私人企业采用静态预期原则调整产量.
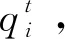
(7)
其中k>0为企业产量的调整参数.
假设2家私企采用静态预期调整产量, 令Φ1=Φ2=0,解得其动态调整模型为
联立(7)~(8)式,建立三寡头产量博弈的离散动态系统:
(9)
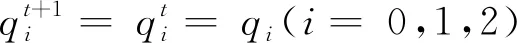
(10)
由(10)式知动态系统有2个均衡点:
其中:E0为边界均衡点,E1为纳什均衡点.
2.2 系统均衡点的稳定性分析
离散动态系统(9)的均衡点的局部稳定性依赖于雅克比矩阵的特征值.经过计算,雅克比矩阵的具体形式如(11)式所示(见附录).我们首先研究E0的稳定性.
定理1边界均衡点E0是不稳定的.
证明将E0代入(11)式可得在均衡点E0处的雅克比矩阵为
J(E0)=
易得矩阵J(E0)的特征值为
因为λ1>1而|λ2|<1,|λ3|<1, 由系统的稳定性理论可知该均衡点不稳定.
现在考虑E1的稳定性.因为d∈(0,1),c0,c1>0,所以2c0+2-d>0, 2c1+2-d>0,从而(2c0+1)(2c1+2+d)>2d2.为简化符号,令A=2c1+2+d,B=2c1+2-d,C=2c0+1.将E1代入(11)式并注意到A-2d-2B=-B,可得
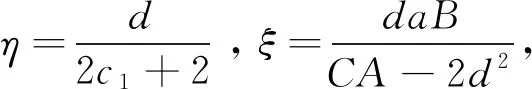
其特征多项式为λ3+A1λ2+A2λ+A3,其中
由Schur-Cohn稳定性条件可知,E1稳定的充分条件为特征多项式J(E1)的系数满足
(12)
定理2纳什均衡点E1稳定的充分条件为
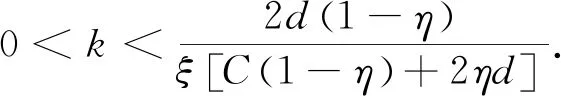
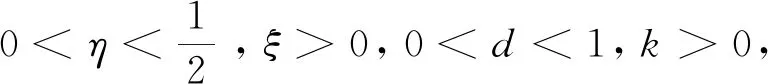
3-A2=3+η2+2ξkη>0.
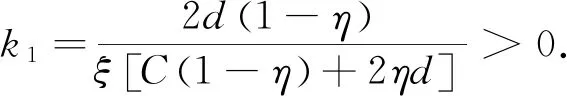
1-A1+A2-A3=
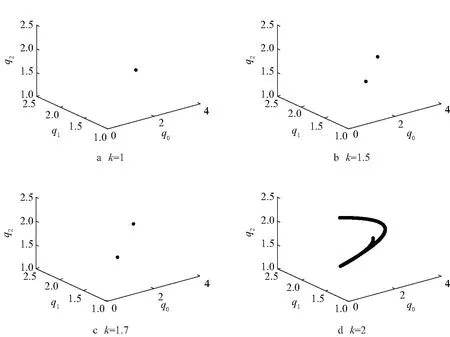
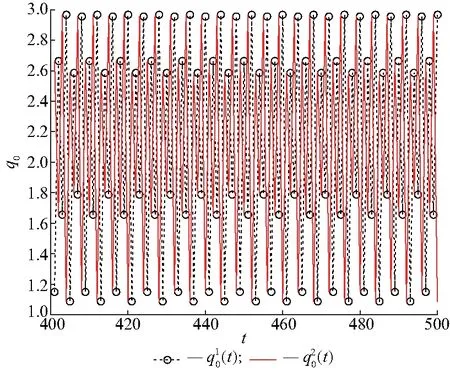
所以1-A1+A2-A3>0等价于k f(k)=B1k2+B2k+B3, 其中 B3=2+η2-η4. 由于f(k)是一个关于k的二元一次方程且B1<0,B3>0,故f(k)=0有2个实数根k2和k3,其中k2<0,k3>k1.所以当0 综上所述, 当0 本节对非线性动力系统(9)的动力学演化过程进行数值模拟, 包括分岔图、最大李雅普诺夫指数、奇异吸引子以及对初始条件的敏感性. 图1给出了动态系统(9)的倍周期分岔过程.从图1可以看出,当国有企业的产量调节速度0 图2显示了动态系统(9)相应的最大李雅普诺夫指数.与图1类似,图2也展示了系统的分岔和混沌行为. 可以观察到, 当k值达到1.25时, 系统出现倍周期分岔, 然后随着k值的增加系统变为混沌. 图1 关于参数k的分岔图 图2 最大李雅普诺夫指数 图3为系统关于不同调节系数k的三维位相图.图3详细地描述了系统(9)的运行轨道,它显示了动态系统的分岔过程,奇异吸引子如图3a所示. 图3 系统关于不同调节系数k的三维位相图 图4展示了当产量调节参数k=2时,系统(9)在时间区间[400, 500]内对初始条件的敏感依赖性, 这是混沌行为的主要特征之一. 图4绘制了2个轨道, 其中国有企业的初值有所变化,私人企业的初值不变,具体赋值为 图4 系统(9)对初始条件的敏感依赖性 图中虚线代表国有企业的产量,实线代表私人企业的产量. 可以清楚地看到, 即使国有企业的初始产量产生微弱的变化, 经过一系列迭代后, 该变化也会对所有企业产生巨大的影响.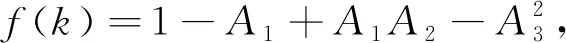
3 数值模拟