改进鲸鱼优化算法的空间直线度误差评定
2022-07-18陈玉韩波许高齐阚延鹏赵转哲
陈玉,韩波,许高齐,阚延鹏,赵转哲
(安徽工程大学 机械与汽车工程学院,安徽芜湖 241000)
空间直线度误差是回转体零件误差评定的一项重要参数,是反映零件加工质量的重要参数之一。国标GB/T11336-2004中规定,空间直线度误差的评定方法主要有3种,包括两端点连线法、最小二乘法、最小区域法。其中最小区域法是3种评定方法中精度最高的,也是唯一满足最小条件原则的评定方法[1]。在运用最小区域法的空间直线度误差评定过程中,主要是找到包容所有实际直线轮廓点且直径最小的圆柱面,包容所有实际直线轮廓点的圆柱面有无数个,但直径最小的只有一个。因此,空间直线度误差评定的计算问题实质上属于最优化问题,对于最优化问题,传统的数学处理方法对其求解困难,而智能优化算法在求解优化问题上具有较大优势,近年国内外诸多学者将多种不同的智能优化算法应用在空间直线度误差评定中[2]。陈君宝等[3]将变步长天牛须搜索算法应用于空间直线度误差中,通过实验验证,该算法能有效的应用于空间直线度误差评定中。杨洋等[4]在满足最小区域条件下,建立了空间直线度误差的数学模型,并对教与学算法进行改进,同时将该算法与最小区域法相结合,提高了评定精度。温银萍[5]为解决轴线直线度误差时难以确定基准轴线的问题,在满足最小条件准则的基础上,将动态步长细菌觅食算法应用于液压缸的轴线直线度误差评定,其求解精度提高了6.1%~72.6%左右。杨俊超等[6]对深孔轴线直线度误差评定理论进行分析,提出正方网格迭代寻优算法评定轴线直线度。
上述算法都不同程度上提高了空间直线度误差评定的精度,但这些算法在求解过程中算法自身参数的选择对求解结果影响较大,且仍存在着易陷入局部最优、稳定性不高等问题。鲸鱼优化算法(Whale optimization algorithm,WOA)是2016年由澳大利亚学者Mirjalili根据座头鲸的捕食习性开发的一种新型群智能优化算法,该算法具有调节参数少、稳定性高等优点,经研究表明该算法的性能丝毫不逊色于其他群智能优化算法[7]。该算法与其他群智能算法一样,存在着易陷入局部最优、后期收敛速度慢等问题,因此,为进一步提高该算法的优化性能,本文对基本鲸鱼优化算法的3个方面进行改进,采用拉丁超立方体抽样方法(Latin hypercube sampling,LHS)进行种群初始化,将非线性收敛因子替代基本WOA算法中的线性收敛因子,最后将非线性惯性权重引入鲸鱼优化算法,以进一步提高算法的求解精度和速度。本文在满足最小区域条件的基础上,将改进后的鲸鱼优化算法应用于空间直线度误差评定中。
1 空间直线度误差评定数学模型
本文以最小包容区域法为基础,建立空间直线度误差评定数学模型。最小包容区域法是以包容所有实际被测直线轮廓点且直径最小的包容圆柱的轴线为基准轴线,该圆柱的直径即为空间直线度误差,其示意图如图1所示。

图1 空间直线度误差评定示意图
如图1所示,根据最小包容区域法定义,建立空间直线度数学模型。设基准轴线L的空间直线方程为

(1)
式中:l,m,n为基准轴线的方向向量;(x0,y0,z0)是基准轴线上的定点。根据空间点到直线距离公式,可得实际直线轮廓点到基准轴线的距离,表达式为
(2)
式(2)中实际直线轮廓点到基准轴线的最大距离dmax,即为包容区域圆柱的半径,而空间直线度误差为包容区域圆柱的直径,由最小包容区域法的定义可知,需找寻直径最小的包容区域圆柱,可得空间直线度误差的目标函数为
F(x0,y0,z0,l,m,n)=min(2·dmax)
(3)
利用数学计算方法对上式进行优化求解,可得出基准轴线方程的6个参数,进一步可求出空间直线度误差。从式(3)可看出,最小包容区域法评定空间直线度误差其是实质为极大值极小化的优化求解问题。
2 基本鲸鱼优化算法
WOA算法有着稳定性强、调节参数少等优点,被广泛应用于工程问题中。根据座头鲸的捕食习性,WOA算法主要包括3个阶段:包围捕食、气泡网捕食和随机搜索捕食。各阶段数学模型如下[7]:
1) 包围捕食
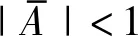
(4)
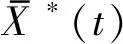
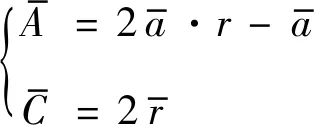
(5)
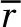
(6)
2) 气泡网捕食
在该阶段中,WOA算法设置了两种捕食机制以模拟该阶段座头鲸的捕食特点,包括收缩包围机制和螺旋气泡捕食机制。收缩包围机制通过式(4)进行位置更新,螺旋气泡捕食机制是模拟座头鲸们以螺旋式轨迹游动捕食猎物的特点,在WOA算法中采用对数螺旋方程来描述这种行为,其位置更新公式为:
(7)

因座头鲸在捕食猎物时,在猎物收缩包围圈内沿螺旋式轨迹绕着猎物游动,为模拟这种捕食特点,在WOA算法中,假设选择螺旋气泡捕食机制与收缩包围机制来更新座头鲸位置的几率均为50%,其位置更新为:
(8)
3) 随机搜索捕食
(9)
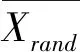
3 改进的鲸鱼优化算法
本文为提高WOA算法的寻优性能,对WOA算法的3个方面进行改进,首先利用拉丁超立方体抽样方法初始化种群,增强WOA算法的种群多样性;再将非线性收敛因子取代基本WOA算法中的线性收敛因子,进一步提高算法寻优能力;最后将非线性惯性权重引入WOA算法中。以下将改进的鲸鱼优化算法记为LTWWOA算法。
3.1 LHS方法初始化种群
文献[8]指出,群智能优化算法的种群初始化的好坏对算法的寻优能力有着重要影响。在基本WOA算法中,采用随机的方法产生初始化种群,这种方法产生的初始化种群易导致产生的种群个体分布不均和出现个体重叠,在一定程度上降低了算法的寻优性能[9]。LHS是常用的抽样试验统计学抽样方法,具有如下特点:
1) 能实现满空间填充,产生的采样点个体具有随机性,并能较好的将其均匀分布在搜索空间中;
2) 稳定性强,希望采样点总均值可提供无偏估计,同时方差小。
从LHS方法的特点看,若采用LHS方法初始化种群,既可以保证产生的初始化种群个体的随机性,又可以保证种群个体能较均匀的分布在搜索空间中,从而保证了种群的多样性,在一定程度上提高了算法的寻优性能。本文运用LHS方法初始化种群。

步骤1 确定种群规模S;
步骤3 生成S行h列的且每一列都为{1,2,…,S}的一个随机全排列矩阵AS×h;
步骤4 矩阵AS×h的每行对应一个小超立方体,从每一个小超立方体中选取一个种群个体,这样就可以得到S个互不相同的种群个体。
图2和图3分别为采用LHS方法产生的样本点图和随机方法产生的样本图,抽样规模为S=20,维度h=2,由图2和图3可看出,LHS方法产生的样本点能更加均匀的分布在搜索空间中。因此,采用LHS方法对WOA算法进行初始化种群,能有效的保证了种群个体更均匀的分布在搜索空间中,提高了种群多样性,一定程度上提高了算法寻优性能,避免算法过早收敛。
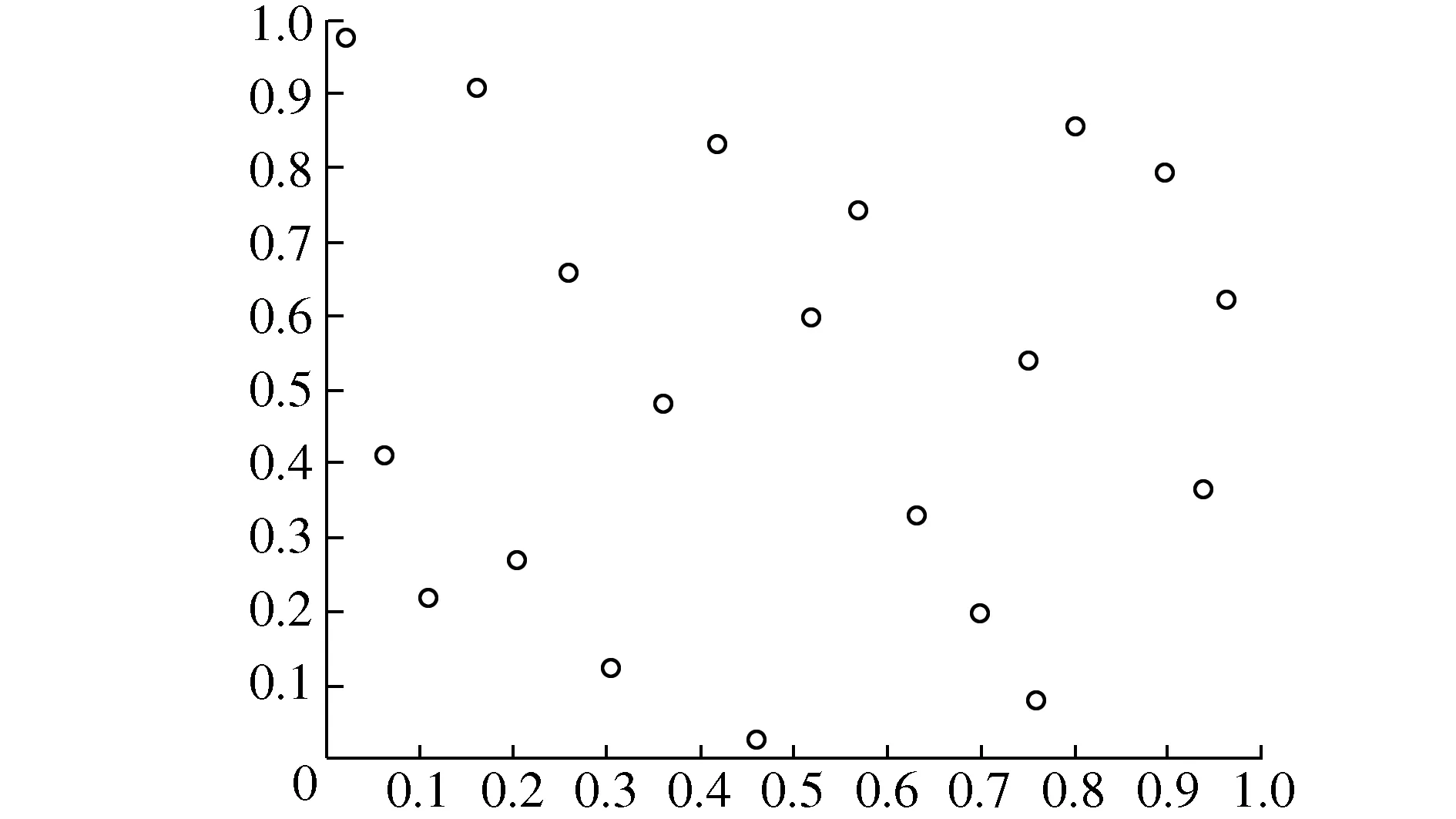
图2 采用LHS方法样本点图
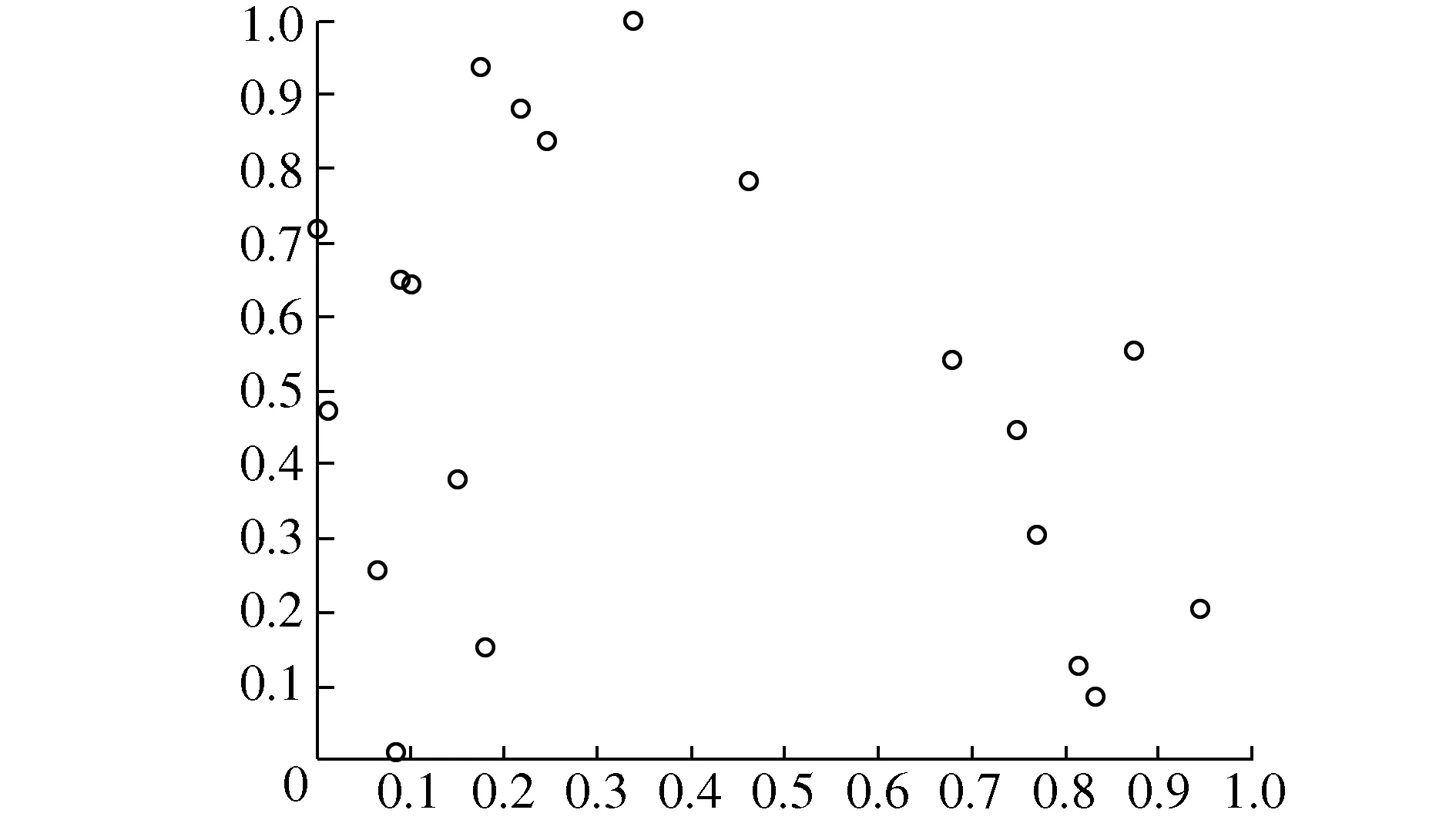
图3 采用随机方法样本点图
3.2 收敛因子的改进
由式(6)可得,在基本WOA算法中,收敛因子a随着算法迭代次数的增加由2线性递减至0,由于这种递减方式在算法迭代过程中,收敛因子a的递减速度全程不变,这易导致算法前期搜索和后期寻优失衡,降低算法寻优性能,同时WOA算法的实际寻优过程是一种复杂的非线性过程,收敛因子a随迭代次数呈线性递减,很难适应WOA算法的这种非线性寻优过程。为解决该问题,本文提出一种非线性收敛因子,其数学表达式为
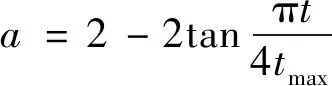
(10)
式中tmax为最大迭代次数。本文取tmax=500时,将改进的收敛因子a与基本WOA算法中的收敛因子a进行对比,对比图如图4所示。
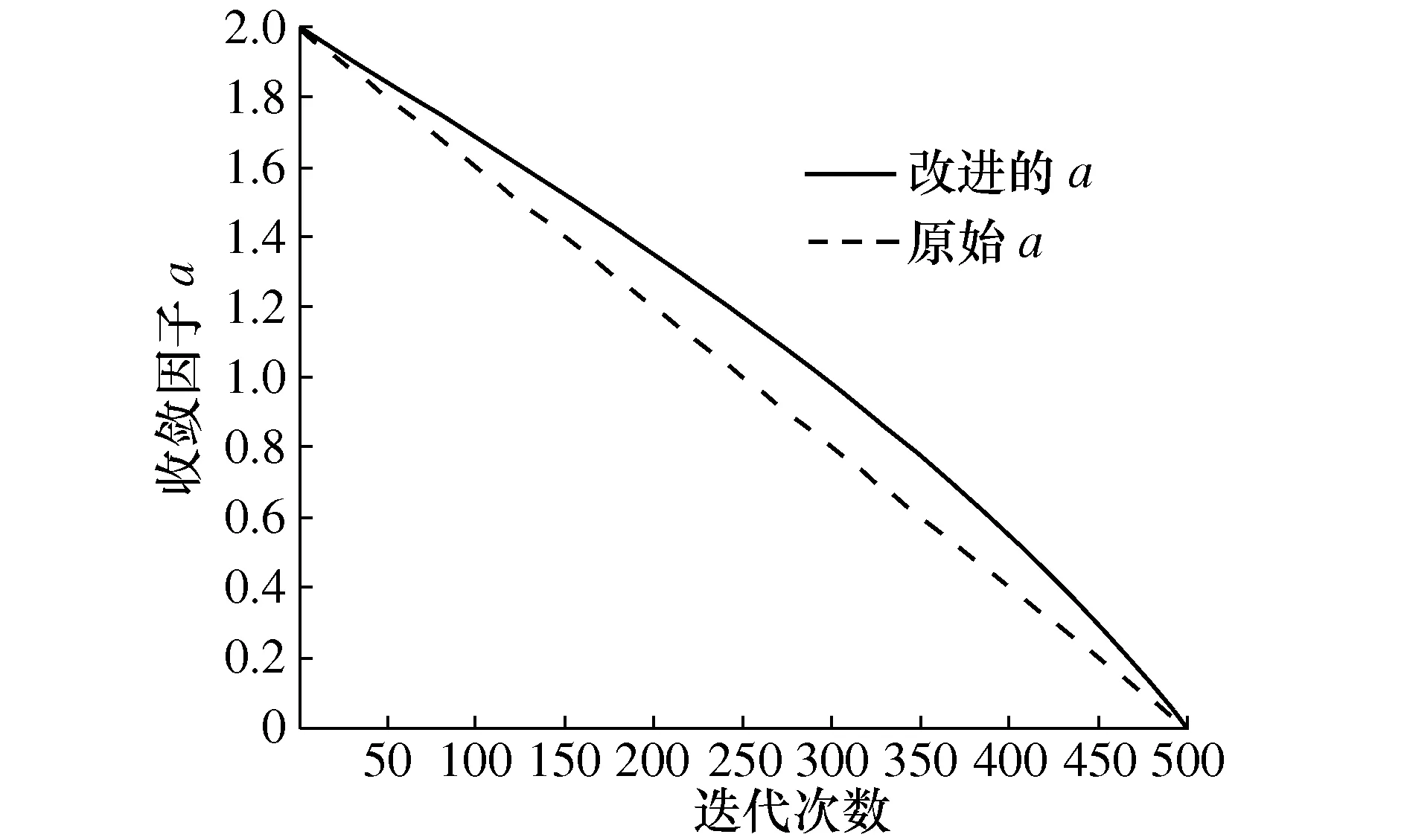
图4 收敛因子a变化对比图
由图4和式(10)可得,基本WOA算法的收敛因子a随算法迭代次数的增加呈线性递减,而本文提出的非线性收敛因子a随算法迭代次数的增加呈非线性递减。这种方式,在算法前期收敛因子a以较小的速度减小,保证了收敛系数A前期值较大,使得座头鲸游走步长大,加快算法全局搜索,到算法迭代后期,收敛因子a以较大的速度减小,使得收敛系数A后期值较小,从而座头鲸游走步长小,使其能在最优解附近进行精确搜索。从而有效的平衡了算法的前期搜索和后期寻优能力。
3.3 非线性惯性权重
Shi等[10]针对粒子群算法的不足,将惯性权重引入其中,有效提高了算法的性能。研究表明,惯性权重的大小对算法的求解效率有一定的影响[11],较大的惯性权重有利于增强算法的全局搜索能力,较小的惯性权重有利于增强算法的局部搜索能力[12]。基本WOA算法的寻优求解过程,其权重始终是固定值为1,容易导致座头鲸的位置在最优位置附近徘徊,从而使得WOA算法陷入局部最优解。受文献[13-14]启发,为提高WOA算法的性能,避免其陷入局部最优解,将非线性惯性权重引入WOA算法,非线性惯性权重数学表达式为

(11)
式中:wst是初始惯性权重;wend为最大迭代次数时的惯性权重;k和u是控制系数,对w的范围起调节作用。经大量测试,分别取wst=0.98和wend=0.4,分别取k=0.21和u=11.2时,能使得LTWWOA算法表现性能较好。
根据WOA算法的3个位置更新公式,将非线性惯性权重w引入WOA算法,得到LTWWOA算法的3个位置更新公式为:
3.4 改进的鲸鱼优化算法步骤流程
综合上述,对基本鲸鱼优化算法的三方面进行了改进,首先采用LHS方法进行初始化种群;再将非线性收敛因子替代基本WOA算法中的线性收敛因子,最后将非线性惯性权重引入鲸鱼优化算法中。LTWWOA算法的详细步骤如下:
步骤1 对算法相关参数进行设定:种群规模S,最大迭代次数tmax,初始惯性权重wst,最大迭代次数时惯性权重wend,控制系数k和u等参数;
步骤2 运用LHS方法初始化座头鲸种群,使其能均匀分布在搜索空间中;
步骤3 根据适应度函数,计算每个座头鲸个体的适应度值,并保存最佳适应度值对应的座头鲸个体及其位置;

步骤5 最后判断是否达到结束条件,若达到,则输出最优解;若未达到,则回到步骤3继续进行迭代。
LTWWOA算法流程图如图5所示。
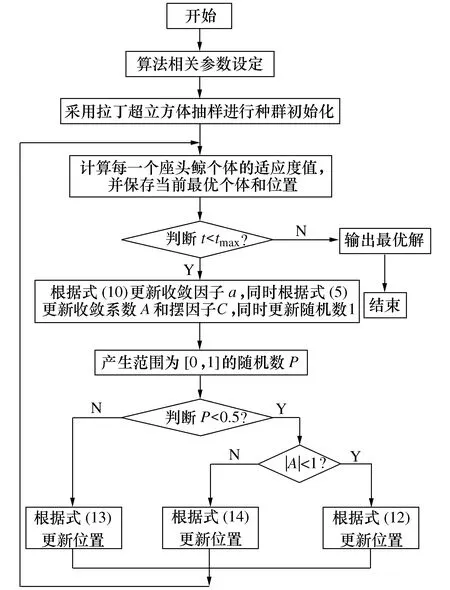
图5 LTWWOA算法流程图
3.5 改进的鲸鱼优化算法的性能测试
1) 算法相关参数设定及测试函数选取
为验证LTWWOA算法的性能,将WOA算法、遗传算法(Genetic algorithm,GA算法)和基本粒子群算法(Particle swarm optimization,PSO算法)与LTWWOA算法根据选取的测试函数进行测试对比。选取文献[6]中的4组单峰函数和4种多峰函数为测试函数,测试函数如表1所示。

表1 测试函数
其中F1~F4为单峰函数,F5~F8为多峰函数,各函数维度均为30,最优解均为0。为保证对比的公平性,各算法的最大迭代次数为1 000,种群规模均为40,GA算法交叉概率设为0.8,变异概率为0.05,PSO算法的学习因子c1=c2=2,LTWWOA算法的wst和wend分别为0.98和0.4,控制系数k和u分别为0.21和11.2。
2) 各算法函数测试结果对比
将各算法在MATLAB2017b软件下独立运行40次,40次测试结果如表2所示,各算法的平均收敛曲线如图6所示。

表2 测试结果对比
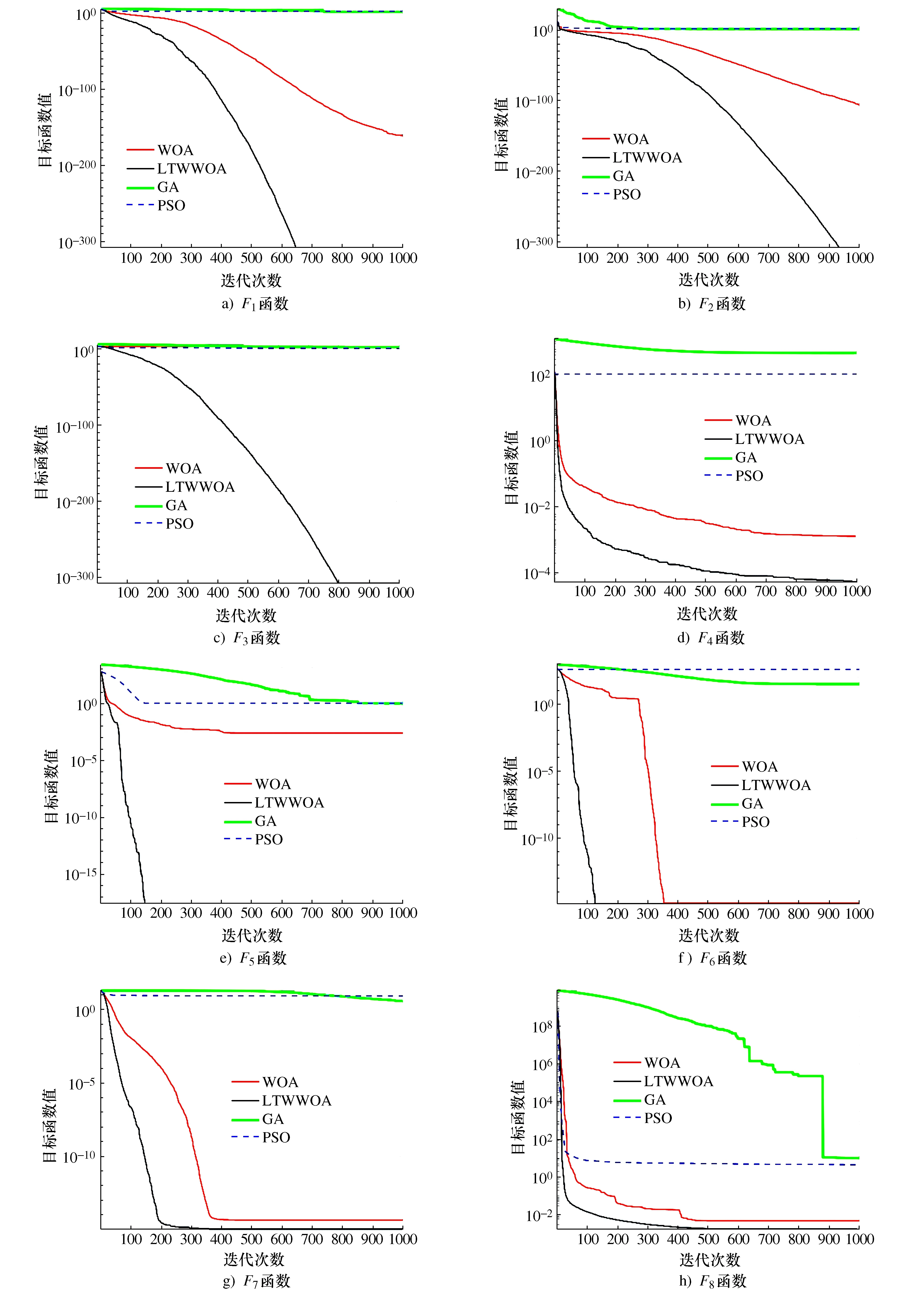
图6 平均收敛曲线对比图
本文以40次测试结果的平均值、标准差和平均收敛曲线分别反映各算法的收敛精度、稳定性和收敛速度。从表2的测试结果来看,LTWWOA算法相比于其他3种算法在平均值、标准差等各方面都有着明显优势,从单峰函数的测试结果来看,对于函数F1~F3的求解,LTWWOA算法都得到了理论最优解0,WOA算法其收敛结果与理论最优解较为接近,而GA算法和PSO算法则表现较差,对于函数F4,虽然LTWWOA算法与WOA算法都未能收敛到最优解,但从测试结果来看,LTWWOA算法相比于WOA算法收敛精度更高,更接近理论最优解;从多峰函数的测试结果来看,GA与PSO算法的求解精度远差于LTWWOA算法的求解精度,对于函数F5和F6的求解,LTWWOA算法得到了理论最优解,虽然WOA算法的40次运行中的最优值达到了理论最优解,但其平均值相比于LTWWOA算法要差,对于函数F7和F8的测试结果中,LTWWOA算法的求解精度也略高于WOA算法。因此,总体来看LTWWOA算法相较于其他3种算法在单、多峰函数的求解精度都要更优秀。再从40次测试结果的标准差来看,对于函数F1、F2、F3、F5、F6的标准差,LTWWOA算法的40次测试结果标准差都为0,相比于其他3种算法都要好,在函数F4、F7和F8的求解中虽然标准差未达到0,但相比于其他算法的标准差都更小,足以证明LTWWOA算法相比于其他3种算法的稳定性更好;从图6的各算法平均收敛曲线来看,LTWWOA算法相比于其他3种算法的收敛速度都更快。
综合上述结果,都充分证明了LTWWOA算法在收敛速度、精度和稳定性上相比于基本WOA算法都得到了提高,同时验证了本文提出的对基本WOA算法3个方面的改进策略是十分有效的,也为后续将LTWWOA算法应用于直线度误差评定奠定基础。
4 实例验证
4.1 实例1
为验证LTWWOA算法能有效应用于空间直线度误差评定中,选用文献[15]中的原始数据,原始坐标数据如表3所示。

表3 原始坐标数据[15]
采用LTWWOA算法、WOA算法和GA算法对该原始数据进行空间直线度误差评定,为保证对比的公正性,各算法参数进行统一设置:种群规模为100,最大迭代次数为500次,维度为6,LTWWOA算法的wst=0.98,wend=0.4,控制系数k=0.21,u=11.2分别为GA算法的交叉概率设为0.8,变异概率设为0.1。各算法在MATLAB2017b软件下独立运行50次,取50次结果的平均值为直线度误差,同时本文引用文献[3]中采用HTLBO算法对该原始数据的评定结果与各算法结果进行对比,各算法得出的基准轴线参数及直线度误差结果如表4所示,平均收敛曲线对比图如图7所示。
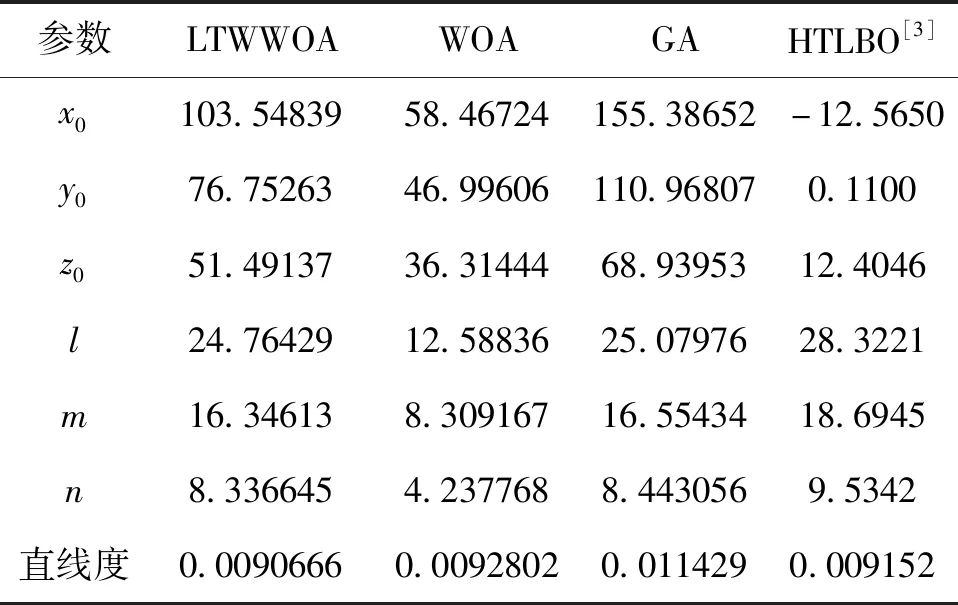
表4 各算法直线度结果 mm
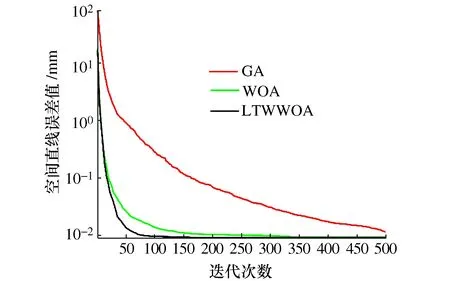
图7 实例1的各算法平均收敛曲线对比图
从表4的结果来看,LTWWOA算法相比于其他3种算法的空间直线度误差评定精度最高,平均直线度误差达到0.009 066 6 mm,50次运行结果中最优解为0.009 023 8 mm,3种算法中GA算法的评定精度最低,LTWWOA算法相比于文献[3]中采用HTLBO算法的结果也要好,从图7的平均收敛曲线来看,LTWWOA算法的收敛速度也要比WOA算法与GA算法更快。
4.2 实例2
为进一步验证LTWWOA算法应用于空间直线度误差评定的优势,通过实验平台对内径为800 mm的无缝钢管的轴线直线度进行测量评定,采集被测钢管的7组截面数据,得到7组截面中心坐标,其实验数据如表5所示。

表5 各截面中心坐标实验数据 mm
根据第1节中建立的空间直线度误差数学模型,以最小区域法为原则,分别采用LTWWOA算法、WOA算法、GA算法和PSO算法对上述数据进行轴线直线度评定,同时将传统直线度评定方法中的两端点连线法与其他算法得出的结果进行对比。各算法的种群规模都设置为100,最大迭代次数设置为500,维度为6,LTWWOA算法的wst=0.98和wend=0.4,控制系数k=0.21,u=11.2,GA算法的交叉概率设为0.8,变异概率设为0.05,PSO算法的学习因子c1=c2=1.5,各算法在MATLAB2017b下独立运行40次,取40次运行结果的平均值为直线度。各算法得出的基准轴线参数及直线度评定结果如表6,对应的平均收敛曲线对比图如图8,因数据跨距较大,纵坐标采用对数形式。
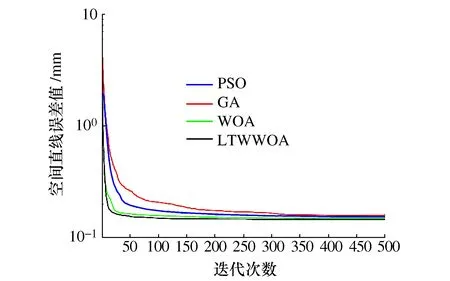
图8 实例2的各算法平均收敛曲线对比图
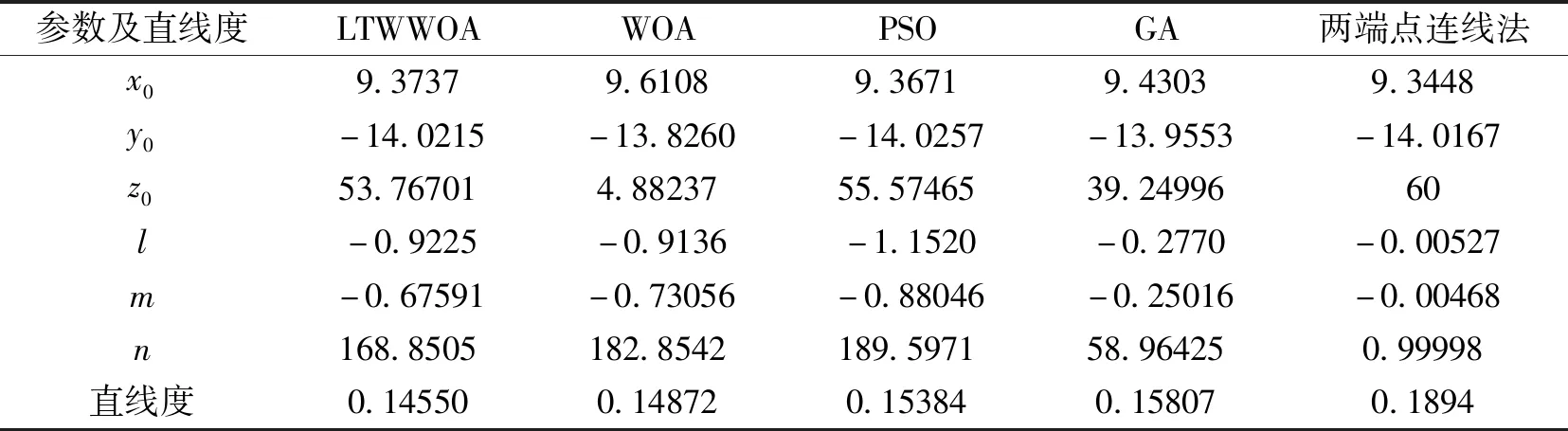
表6 各算法评定直线度结果 mm
从表6的结果可看出,传统的两端点连线法在对空间直线度评定中精度最低,相比于其他3种智能算法LTWWOA算法的评定精度最高,40次运行得出的空间直线度平均值为0.145 50 mm,其中40次运行结果中最优解为0.141 43 mm。从图8来看,LTWWOA算法相比于其他3种算法在收敛速度上也更快。
5 结论
为解决传统数学方法在求解空间直线度误差中存在求解困难且求解精度不高的问题,本文以最小区域法为基础,将改进的WOA算法应用于空间直线度误差评定中,有效提高了求解精度。得出以下结论:
1) 针对WOA算法的不足,对WOA算法进行三方面改进,以LHS方法初始化种群,将非线性收敛因子替代基本WOA算法中的线性收敛因子,最后将非线性惯性权重引入WOA算法中。利用测试函数对改进的WOA算法进行性能测试,验证了改进的WOA算法在收敛速度、精度和稳定性得到了提高。
2) 通过两个实例验证LTWWOA算法能正确有效地应用于空间直线度误差评定。将不同算法的求解结果进行对比,得出LTWWOA算法相比于传统方法和其他算法在收敛速度和求解精度上都更有优势。
