工业机器人关节传动系统机电耦合振动特性分析
2022-07-18仪凌霄王之海柳小勤赖泽浪
仪凌霄,王之海*,,柳小勤,赖泽浪
(1.昆明理工大学 机电工程学院,昆明 650500;2.云南省先进装备智能制造技术重点实验室,昆明 650500)
工业机器人关节的良好性能是确保正常作业的前提,但目前工业机器人普遍存在长期作业精度问题,初期投入使用虽能够较好的执行控制系统的规划路径,但由于设计之初较少考虑电气、机械参数等对关节振动的影响,关节谐振发展趋于严重,以致停机,造成经济损失甚至波及人身安全。由于关节传动系统存在电气和机械参数而引起的机电耦合现象,表现出复杂的动力学特性。当系统振动频率与机械部件的振动频率较接近或相互叠加时,发生的共振将影响机械臂的控制精度、可靠性和传动平稳性,因此对工业机器人关节机电耦合振动建模方法的研究具有重要意义。
辛大奇等[1]针对工业机械臂机电参数匹配不当问题,建立伺服传动系统的机电耦模型,分析了不同的电机、机械参数组合对工业机器人振动的影响,但并未分析机电耦合对关节末端振动的影响。林利红等[2]建立了同步伺服驱动系统的机电耦合振动模型,仿真分析了电流调节器参数、谐波扰动等对机电耦合振动动态过程的影响。Kim等[3]从控制角度对机械臂的加工精度和运行的稳定性进行研究,但忽略了关节元器件对传动系统振动的影响。Concordia[4]研究了电机定子与转子之间的电磁参数,考虑了电机绕组与传动系统的扭振与电流振荡之间的耦合效应,建立关节传动机电耦合模型,却没考虑机械参数对关节系统振动影响的问题。
综上,本文将对工业机器人关节传动系统开展建模仿真,分析关节系统扭振、机电耦合等振动特性,同时考虑机械参数对关节系统的影响,以及各元器件对工业机器人传动系统的振动影响。
1 关节传动系统模型
1.1 传动系统动力学模型
工业机器人的关节传动系统主要包括机械传动系统、驱动系统和控制系统,为了便于分析,可将关节系统简化为“电机-减速机-负载”三惯量系统[5],如图1。图中Je,Jm,JL分别为电机、减速器和负载转动惯量。C1,C2,C3分别为电机、减速机和负载粘滞阻尼系数。Te,TW1,TW2,Tm分别为电机电磁转矩、轴1、2的扭矩和负载转矩;CW1,CW2分别为轴1、2的粘滞阻尼系数;KW1,KW2分别为轴1、2的刚度系数。
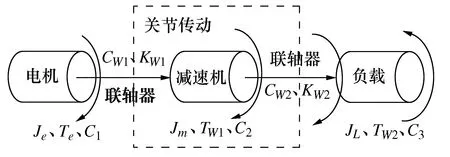
图1 关节系统机电耦合动力学模型
如图1所示,关节驱动系统由电机、减速机、负载、联轴器组成。控制系统牵引电机旋转,通过减速机与传动轴驱动负载。
关节传动系统力矩平衡方程:

(1)
式中:i为减速机的减速比;Δθ为关节前后角度差。
1.2 电机控制模型
针对本文仿真研究对象钱江QJR6-1型六自由度串联工业机器人伺服控制系统的控制特点,开展永磁同步电机的转子磁链定向的建模工作。由于永磁同步电动机(PMSM)属于高阶[6]、非线性、强耦合的复杂系统,主要由电机本体、逆变器、电流控制器等组成。由三相交流电的旋转磁动势形成电枢磁场,一方面切割定子绕组而产生感应电动势,另一方面以电磁力拖动转子同步旋转,根据电磁感应原理磁链的变化会感应出电压,包括定子绕组中的反电动势和旋转耦合电势,会影响电压对定子电流的调节作用。设电机三相绕组分别为A、B、C,且各绕组中心线在与转子垂直的平面上。现用拉格朗日-麦克斯韦方程建立永磁同步电机电压方程[7],即
(2)
式中:uA、uB、uC为A、B、C相定子电压;iA、iB、iC为A、B、C相定子电流;eA、eB、eC为永磁体磁场在A、B、C相电枢绕组中感应的旋转电动势;R为定子绕组自感;P为微分算子LA、LB、LC为定子绕组自感;MAB、MBC、MCA为绕组之间的互感。
(3)
式中:Lα为定子绕组的漏感;Lφ为定子绕组自感的平均值;Lγ定子绕组自感的二次谐波值。
(4)
与定子A、B、C三相绕组交链的永磁体磁链:
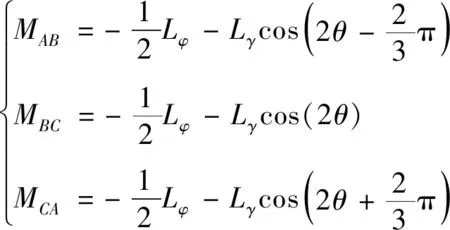
(5)
式中:ψFM为与定子A、B、C相绕组交链的永磁体磁链的幅值;θ为绕组轴线与永磁体基波磁场轴线之间的电角度。
永磁体磁场在定子A、B、C相绕组中感应的电动势eA、eB、eC为:
(6)
设两相同步旋转坐标系的d轴与三相静止坐标系的A轴的夹角为θ,如图2所示,其中ABC为自然坐标系,d-q为同步旋转坐标系。

图2 各坐标系关系
取d轴方向与永磁体基波磁场轴线的方向一致,则从三相静止坐标系A-B-C到两相旋转坐标系d-q的变化矩阵为
(7)
利用式(7)的变换矩阵,把电机在三相静止坐标系下的电压方程变换到同步旋转坐标系下的电压方程为

(8)
式中:ud、uq为d、q轴定子电压;id、iq为d、q轴定子电流;Ld、Lq为定子绕组的电感。
从以上坐标变换过程可得电磁转矩Te的表达式为
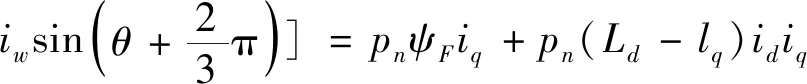
(9)
式中:第一项为永磁体q轴电流作用产生的永磁转矩;第二项为磁阻转矩。
1.3 机电耦合模型
在关节驱动伺服系统中存在电气驱动的电气参数与机械传动系统力学因素的强耦合[8-12]。
图3所示的全局耦合模型包括了驱动系统、传动系统、控制系统、反馈系统等。伺服电机电磁参数与传动系统力学参数的耦合。通常表现为电磁转矩耦合与谐波转矩耦合。
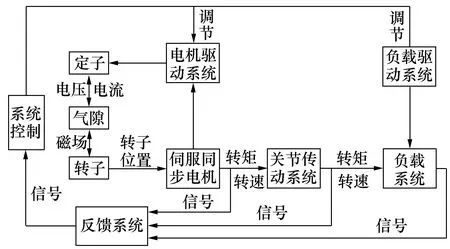
图3 关节系统机电耦合模型
电磁转矩耦合即电机电磁转矩经传动装置驱动负载运动,该耦合形式的方程描述为:
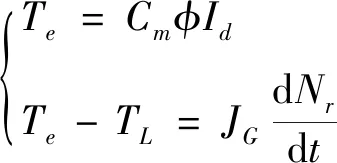
(10)
式中:Te为电动机电磁转矩;Cm为电动机电磁转矩常数;φ为电动机磁通;Id为电动机电枢电流;TL为电动机传动轴的等效负载转矩;Nr为电动机转速;JG为电机转子和传动装置端的总转动惯量。
谐波转矩耦合是由晶闸管交流装置给伺服电机供电,在伺服电机的主回路中将产生谐波电流Δid:
(11)
式中:Ij为谐波电流幅值;j为谐波次数;θj为谐波旋转角度。
谐波电流作用到电机产生的谐波电磁转ΔMa
(12)
谐波转矩使传动系统产生同频扭振而会对系统产生扰动。
通过以上分析可列出关节系统机电耦合动力学方程:

(13)
式中:θ1,θ2,θ3分别为永磁同步电机、减速机和负载的旋转角度。
2 关节系统扭转振动分析
2.1 传动系统扭振
由于减速机转动惯量较小可以忽略不计,故将QJR6-1型工业机器人关节系统简化为电机和负载双惯量系统模型[13],电机端转动惯量Je=0.01 kg·m2、轴系刚度k=2 000 Nm/rad,工业机器人末端承重范围0~5 kg,考虑实际负载工况,将仿真负载端转动惯量设置为JL=0.08 kg·m2,关节系统双惯量模型如图4所示。

图4 关节系统双惯量模型
由式(13)推导出电机转速、负载转速与电机电磁转矩的传递函数:
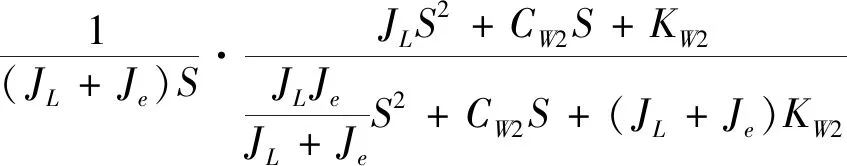
(14)

(15)
由式(14)与式(15)传递函数可以分为惯性环节、二阶振荡环节两部分。在低频段中,传递函数可以简化为1/(JL+Je)S,系统可视为单惯量系统,此时关节系统不存在扭转振动的问题,而在中高频段中,二阶振荡环节不可忽略,表征关节系统柔性连接的部分。其在S平面中引入的一对共扼复根是产生扭转振动的根本原因[14]。工作时,系统弹性传动轴会产生扭转变形,其表现为传动轴两端转角差振荡。将式(14)变形得
(16)
式中:ωZ、ωP分别为无阻尼谐振自然频率、无阻尼抗谐振自然频率;ξZ、ξP分别为谐振阻尼、抗谐振阻尼。
令式(16)分母为零,可得系统谐振频率fN
(17)
令式(16)分子为零,可得抗谐振频率fA
(18)
由图5所示,该关节系统存在一个谐振频率点(75.46 Hz)和一个抗谐振频率点(25.18 Hz)。G1(S)传递函数所对应系统固有频率处,系统增益突然增加,幅角从-90°突变到-270°,传递函数的增益突然增高,输出量ω2受输入量Te的影响最大,且速度ω2随电磁转矩Te而变化。G2(S)传递函数对应系统相位在抗谐振频率fA处迅速增加,幅值增益更大,且抗谐振频率点对谐振频率点的抑制作用很小。若外界电气控制频率接近谐振频率时,会导致关节轴的剧烈变化而引起关节系统振荡。
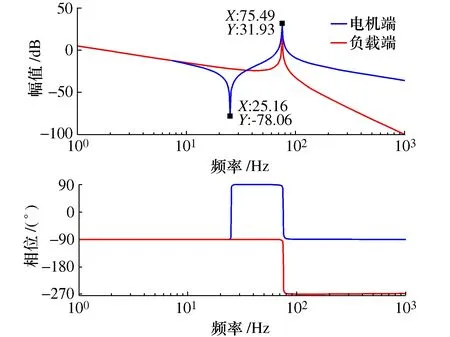
图5 系统伯德图
由图6可知,关节传动系统的一对共轭极点位于左半S平面,系统处于稳定状态。
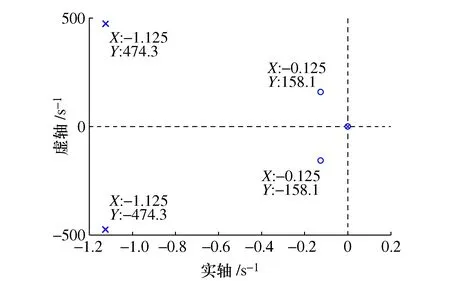
图6 系统零极点图
2.2 机械参数对扭振的影响
由式(17)与式(18)可知,影响系统谐振频率以及幅度的主要参数为刚度与转动惯量,如图7所示。随着刚度增大与转动惯量的降低,谐振频率增加且增加的速度减缓。
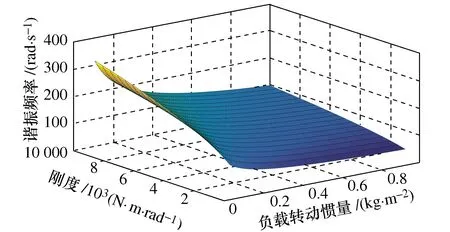
图7 影响谐振频率的参数图
当其他参数不变时,谐振频率的大小只取决于轴的扭转刚度KW。分别取轴的扭转刚度KW1=5 000 N·m/rad,KW2=7 000 N·m/rad和KW3=9 000 N·m/rad时,观察系统谐振频率的变化如图8所示,扭转刚度与谐振频率成正比关系,刚度系数KW越大,谐振频率越高,系统的动态性能也就越好。
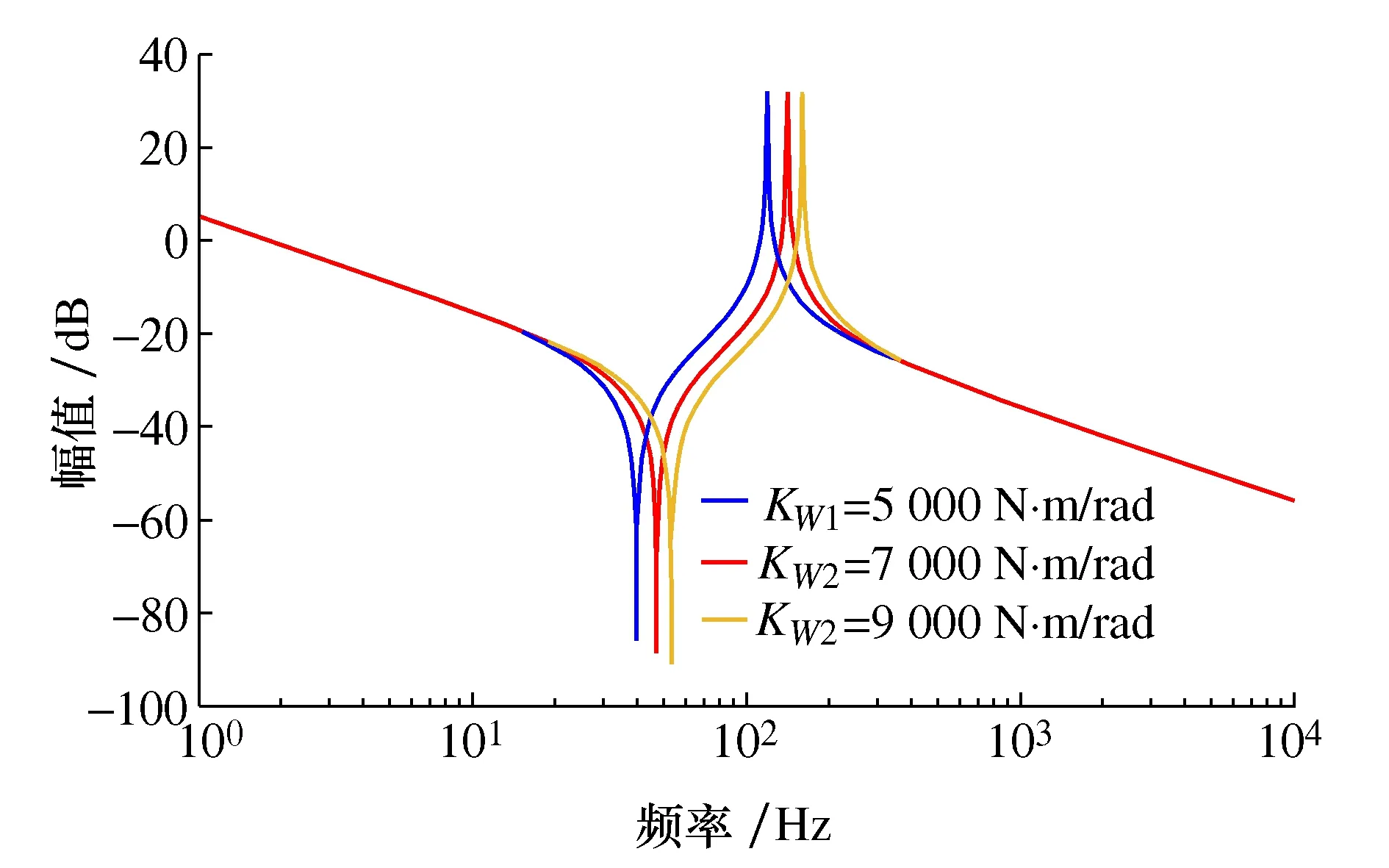
图8 刚度与谐振频率关系图


图9 惯量比R与谐振频率关系图
由图9可知,随惯量比R的增大,谐振频率越来越小,谐振频率与抗谐振频率差值越来越大,抗谐振频率离谐振频率越远,对谐振频率抑制作用也越小。
电机与负载的转速差最能反映系统扭转振动。调节刚度、负载转动惯量等参数,如图10和图11所示,转速差均出现了衰减振动。

图10 不同刚度电机-负载转速差波形图

图11 不同负载转动惯量电机-负载转速差波形图
从图10可以看出,关节长时间工作而产生磨损,使轴系扭转刚度发生变化,现改变轴系刚度,增大扭转刚度10倍,关节系统的振动持续时间由1.3 s减小到0.4 s,而电机与负载转速差由20 r/min减小到6 r/min,振动时间缩短,系统性能得到提升。图11为关节处于重载与空载时,设置负载转动惯量JL分别为1与0.85,振动持续时间由1.2 s增加到了2 s,但电机与负载转速差振动幅值由20 r/min减小到9 r/min,振动幅度有所衰减。
3 传动系统振动机电耦合仿真
3.1 传动系统机电耦合仿真
关节传动系统机电耦合仿真模型如图12所示,仿真模型采用双闭环控制系统,包括:电流环、速度环PI调节器、SVPWM逆变器、逆变桥 Universal Bridge、PMSM模块与机械传动模块等。
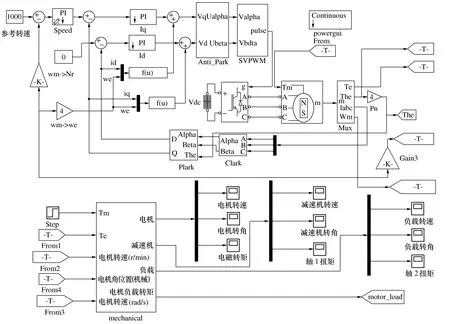
图12 关节传动系统机电耦合仿真模型
本文仿真主要参数来自钱江QJR6-1型号工业机器人的伺服驱动系统、减速机的已知参数。其中,伺服驱动系统由汉桥交流伺服电机(130SFM-E15015-3A2)及汉桥驱动器(HS100M2-N)构成,关节减速机为PG115-10行星减速机。系统主要参数见表1。
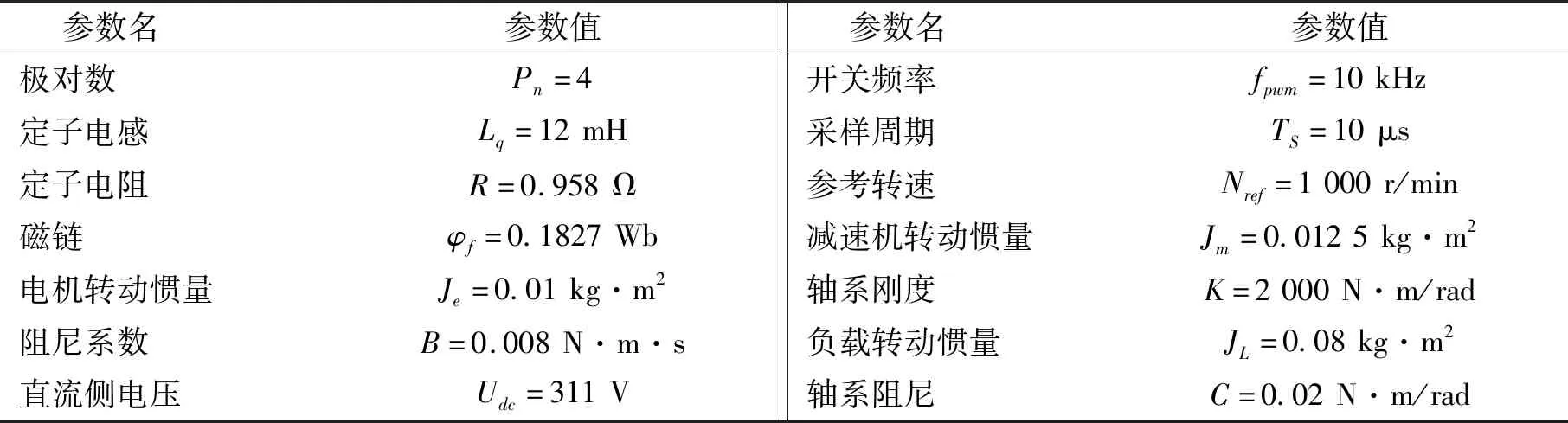
表1 系统主要参数
3.2 机电耦合脉振分析
关节电机中由于电流谐波导致转矩脉振现象。由式(9)知,关节电机的转矩由直轴电流id和交轴电流iq共同决定。对id=0控制策略,可将式(9)写为
(19)
由式(19)知,当电机发生转矩脉振时,电磁转矩随电流信号发生振荡现象。
如图13,在启动过程中,电机电流的波动较大,在0.2 s后趋于稳定。图14中电磁转矩随电流信号变化,在0.2 s后趋于稳定阶段前,存在明显的转矩脉振动现象。为观察高次谐波对电磁转矩的脉振影响,取图13电流响应的稳定阶段(1.5~2 s),进行快速傅里叶变换而得到电流谐波信息。
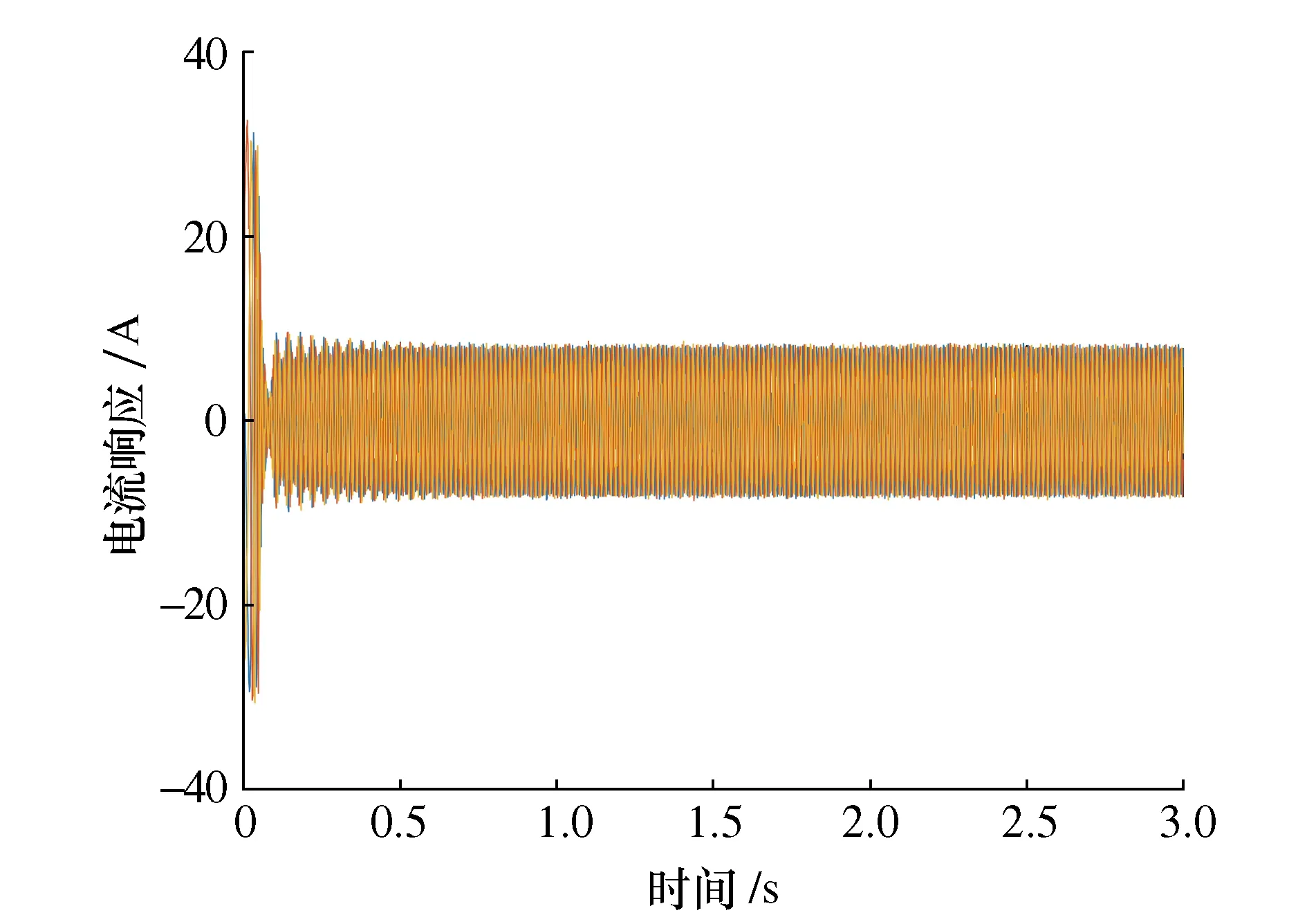
图13 电流响应

图14 电磁转矩
如图15所示,对电流中谐波次数及含量进行分析,其中电流的1次、3次、9次谐波含量较为突出,且电流中含有相当成分的非周期分量和高次谐波分量,高次谐波中以3次、和9次谐波为主。
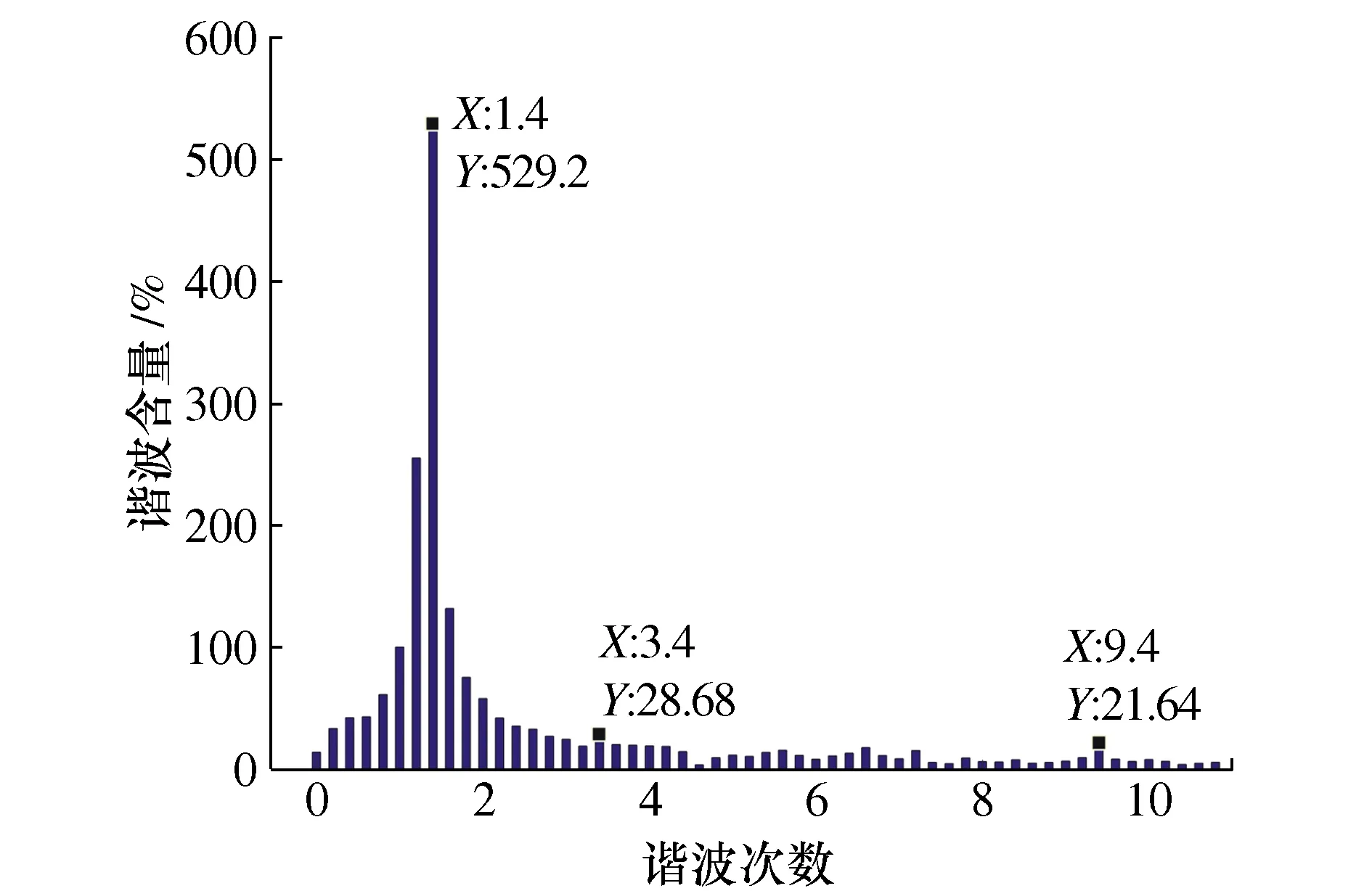
图15 电流谐波含量
3.3 磁参数对传动系统机电耦合振动的影响
由式(19)可知磁参数包含了耦合、扰动、定子电流转矩等重要信息,会对系统振动产生一定影响[15]。当其他参数不变时,改变电机的永磁体磁链系数后的传动系统扭振如图16所示。

图16 磁链系数对关节传动系统振动的影响
如图16系统振动响应,其中设置磁链参数值为ψ1=0.182 7 Wb、ψ2=0.582 7 Wb、ψ3=0.882 7 Wb。随着磁链参数的增大,系统振幅变大,调节时间也相应的变长,磁参数对传动系统振动特性影响较大。通过对于磁参数与电机电磁转矩的仿真分析已验证所建立的关节传动系统机电耦合模型的正确性。
4 关节元器件对传动系统振动影响
将阶跃响应信号作为系统的输入信号,将系统的Step time设置为0,通过各元器件对传动系统的仿真可以得到系统的时、频响应曲线。
4.1 减速机对传动系统的振动影响
如图17给出了减速机在关节传动系统中的时、频域特性。减速机在0.2 s后趋于稳定,振动频率主要分布在0~150 Hz 范围内,减速机在频率12.21 Hz、82.23 Hz、153.7 Hz的振动幅值波动较大,容易引起电气设备共振。
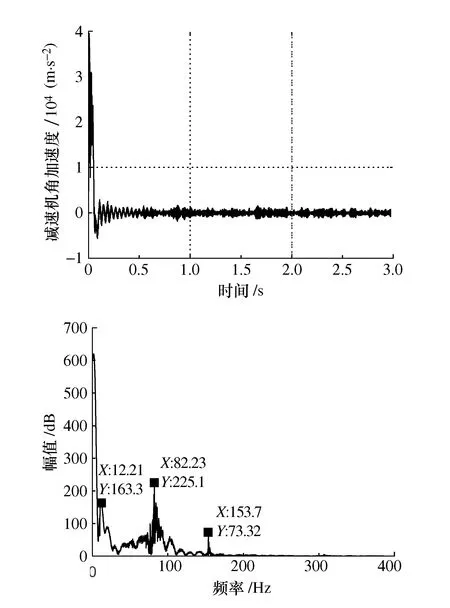
图17 减速机角加速度时、频分析
4.2 联轴器对传动系统的振动影响
图18给出了连接电机与减速机之间的联轴器在传动系统中时、频域振动特性。
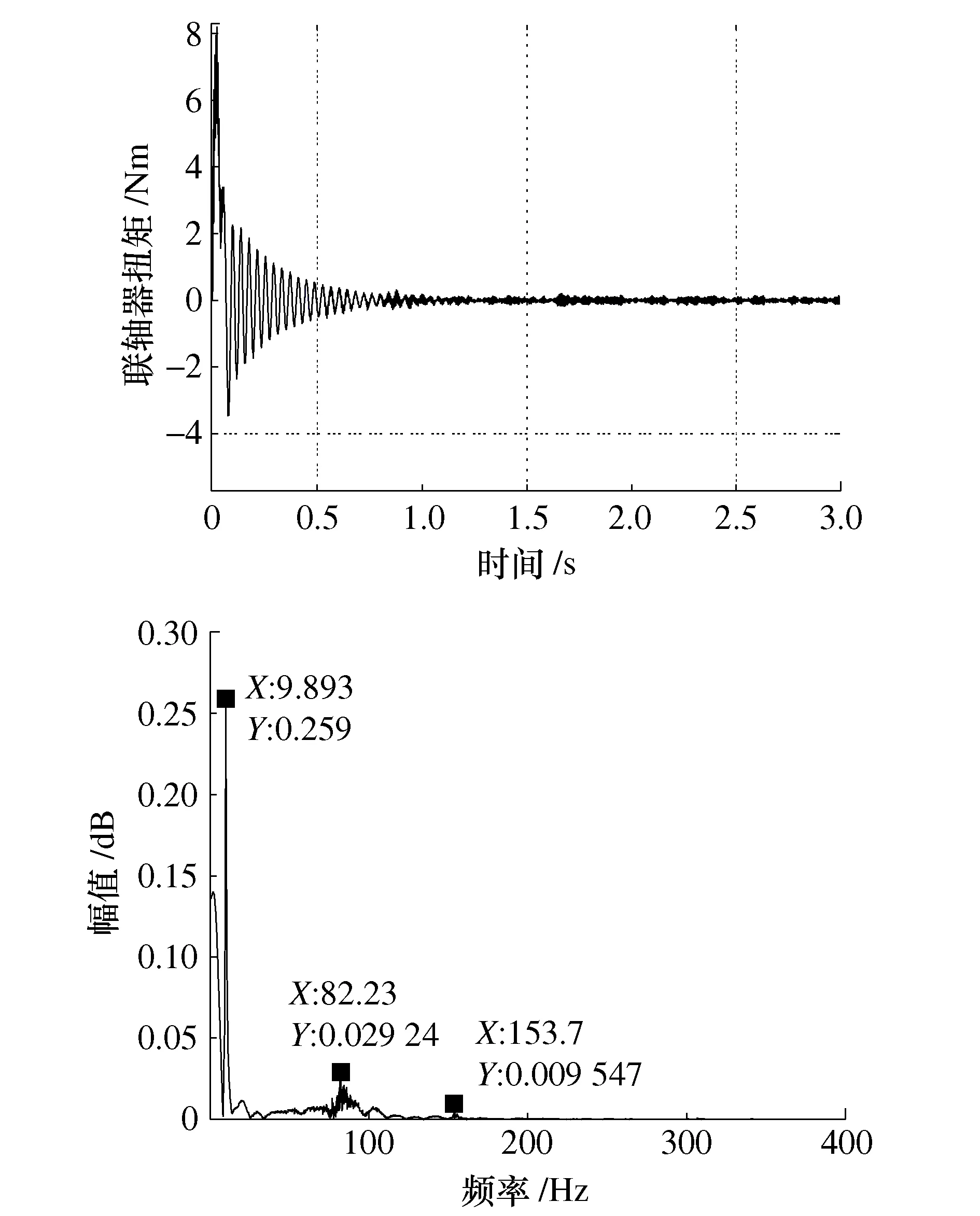
图18 联轴器扭矩时、频分析
通过时域图可以看出联轴器在0.8 s后趋于稳定,由于联轴器受刚度、阻尼等影响为柔性连接,相较与电机的电磁转矩稳定时间,出现了滞后现象,而频域与减速机类似,振动频率基本保持不变,在低频段中,9.8 Hz振动频率幅值最大,也较容易引起共振,但整体振幅强度很小,使联轴器扭矩波动不明显。
4.3 负载对传动系统的振动影响
图19为关节末端恒定负载的时域和频域分布特性。受传动系统的影响,末端趋于稳定的时间相较与减速机有所增长,振动频率范围缩小,整体振动影响较小,其末端性能呈现较为良好。

图19 负载角加速度时、频分析
5 结论
针对工业机器人关节传动系统存在振动现象,本文对关节传动系统开展了机电耦合建模与仿真:
1) 关节传动系统可简化为“电机+减速机+负载”的机电耦合传动模型。
2) 分析关节传动系统的扭转振动特性、机电耦合脉振特性、不同机械参数对系统固有频率及谐振的影响。可知,随着扭转刚度的增大,系统的动态性能变好,随着惯量比的增加,抗谐振频率对谐振抑制作用减小。
3) 通过改变磁链系数、可以有效减小系统振动振幅,并缩短系统调节时间。
4) 考虑了减速机、联轴器、负载等各元器件在关节系统中的振动响应,从关节末端的时、频域分析可获取工业机器人整体性能,本研究可为工业机器人关节系统建模提供有力参考。
