纳米切削镍基单晶合金亚表面缺陷演化机理研究
2022-07-18刘娴萍郝兆朋娄在祯范依航
刘娴萍,郝兆朋,娄在祯,范依航
(长春工业大学 机电工程学院,长春 130012)
镍基单晶合金是航空航天、核电站等装备制造中主要零件材料,严苛的工作环境决定了其需要极高的加工精度和表面质量。亚表面缺陷严重影响零件的使用性能和寿命。充分认识镍基单晶合金加工过程中常见的亚表面缺陷类型,掌握亚表面缺陷的演化机理,找到合适的加工工艺参数[1-3]对获得高质量、高精度、低损伤零件对实际加工有重要的指导意义。
在零件超精密加工材料去除过程中,其切削规律、物理现象与常规切削之间有极大差异,为了研究其切削规律,分子动力学方法[4-5](MD)被广泛应用。Wang等[6]利用MD方法研究了金刚石切削单晶金工件,发现切削过程中工件内部正四面体堆垛层错的形成是由于位错的形核、演化导致的。Gao等[7]研究了单晶铁正交切削过程缺陷演化机理,工件剪切区不断发射位错并且产生了层错和孪晶等缺陷。Zhang等[8]利用MD仿真研究了单晶铜的纳米划痕过程,发现刀具划过工件时,亚表面区域有大量的位错形核。Liu等[9]采用应力方法研究了单晶铜切削过程中亚表面区域的正四面体堆垛层错演化过程。Zimmerman等[10]做了单晶金的MD压痕仿真,并结合实验利用扫描隧道显微镜观察了内部晶体缺陷的变化,分析在压痕过程中单晶金内部“V”型位错的演化机理。Li等[11]对单晶硅纳米切削过程进行了MD仿真,研究了切削速度对加工硅的亚表面损伤的影响。Fang等[12]采用MD方法研究了不同加工参数对Ni/Cu多层膜亚表面损伤的影响,发现降低加工速度会导致工件亚表面出现更多地层错。Wang等[13]研究了单晶铜的纳米切削过程,分析了工件亚表面区域内部各种缺陷的形成机理。
综上所述,亚表面缺陷演化的研究主要集中在单质金属和实验观察层面,取得了一定的、阶段性成果,对于合金的分子建模技术和镍基单晶合金纳米切削过程中出现的亚表面缺陷的类型缺乏研究,对于不同的切削速度对亚表面缺陷演化机理的影响鲜有研究。针对上述情况和实际应用需求,建立氮化硅刀具纳米切削镍基单晶合金的MD模型,对切削过程中出现的各种亚表面缺陷进行分析,为揭示切削速度诱发的亚表面缺陷演化机制等方面开展了相关研究。
1 模型建立
由于纳米切削过程亚表面缺陷演化很难通过实验进行实时观察,并且加工设备要求苛刻,实验成本极高。随着计算机技术飞速发展,分子动力学(MD)方法已经成为研究纳米切削机理的一个重要工具。MD仿真使用Large-scale Atomic/Molecular Massively Parallel Simulator(LAMMPS)[14]进行建模,并采用Ovito软件[15]对模拟结果进行可视化。
块状的氮化硅材料具有高硬度,高耐热性,抗氧化性并有良好的耐磨性,因此氮化硅材料主要用来做研磨的磨削头和切削的刀具。氮化硅刀具常用来切削镍基单晶合金等难加工材料,实际加工发现其切削效率比碳化钨等传统刀具有大幅度提高,并具有良好的经济效益。氮化硅材料分为α-Si3N4与β-Si3N4两种,由于α-Si3N4化学性能不稳定,所以氮化硅陶瓷刀具一般选β-Si3N4[16],因此刀具选定为β-Si3N4刀具。β-Si3N4为密排六方结构,晶格常数a=0.760 8,c=0.291 0,原子层以ABAB的次序沿(0001)方向堆积。刀具前角设置为15°,后角设置为8°,共有4 186个原子组成,为了实现更好地切削效果,刀具圆弧半径设置为3 nm,刀具的具体参数如图1所示。

图1 刀具模型
切削工件为镍基单晶合金。为了简化计算,取其主要的3种组份镍铁铬作合金模型。为了最大程度模拟镍基单晶合金特性,合金模型中Ni、Cr、Fe含量分别为57.75%、31.25%和11%。工件的晶体类型为面心立方晶体结构(FCC),基体尺寸被设置为20 nm×10 nm×4 nm,具体模型如图2所示。

图2 工件模型
工件被分为牛顿层、恒温层、边界层3部分。为了使切削过程中工件内部热传导接近真实情况,恒温层原子遵循Berendsen热动力学,牛顿层原子遵循lammps NVE动力学。为了减小边界效应,x,y方向采用s(shrink-wrapping)边界条件,并将x,y的尺寸做的相对足够大,z方向采用周期性边界条件。具体的MD仿真模型在图3中给出。

图3 切削仿真中Ni-Fe-Cr 合金工件和氮化硅刀具采用的MD模型
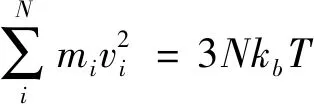

表1 分子动力学切削仿真所取参数
在模拟金属和合金的体系中,EAM势函数被广泛应用[17-18],合金工件中3种原子之间的相互作用采用FeNiCr.eam.alloy势函数,工件中Ni、Fe、Cr原子与刀具的N、Si原子之间的相互作用关系采用Morse势,计算公式为
u(rij)=D[e-2α(rij-r0)-2e-α(rij-r0)]
(1)
式中:D为结合能系数;α为势能曲线梯度系数;r0表示分子间作用力为零时的原子间距。


表2 相同元素之间Morse势函数参数[19-21]

(2)
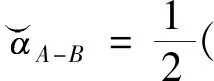
(3)

(4)

经过计算得到不同Morse势函数参数,详细值如表3所示。
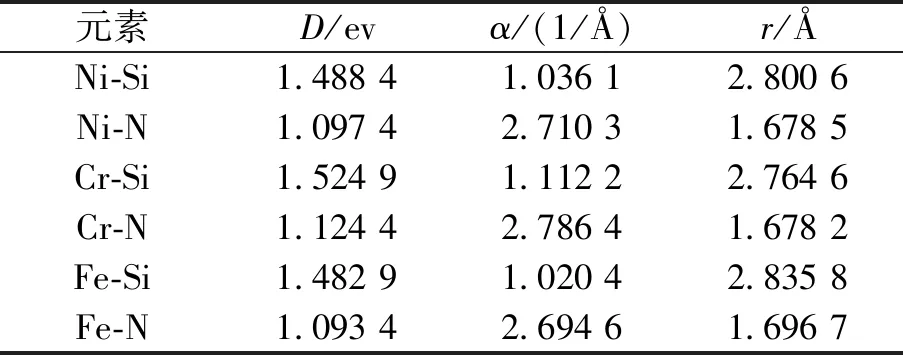
表3 不同元素之间的Morse势函数参数
刀具中N和Si的相互作用采用的是SiN-Tersoff[24-26],Tersoff势函数具体参数如表4所示。

表4 SiN-Tersoff 势函数参数
2 亚表面缺陷
采用可视化软件OVITO[15]的中心对称参数法[27]对仿真结果进行分析,获得亚表面缺陷结构的分布图,对各种位错,层错的分布及其演化进行分析。图4分析了切削速度为20 m/s时,工件内部晶体缺陷的演化。可以发现,随着切削过程的进行,亚表面中出现了大量的缺陷结构。位错在加工亚表面不断扩展,并滑移到工件表面逐渐湮灭。位错的形核与扩展导致工件亚表面晶体缺陷的形成。与此同时,刀具不断向前运动,并给工件施加剪切与挤压作用,剪切区原子不断滑移,沿着前刀面的表层原子被大量切除,切屑不断向前向上扩展,因此加工表面逐渐形成。
采用中心对称参数(CSP)方法,可以很好地识别工件在切削过程形成的晶体缺陷(例如位错与堆垛层错),能够较好地分析工件在切削过程中缺陷变化。中心对称参数是表征晶体有序和无序的一个重要度量。当CSP的值接近零时,表示晶体处于中心对称的位置[27],当CSP为非零时,表示晶体是有无序的,缺陷类型可以通过计算得到[27],计算式为

(5)
式中:No表示被识别原子周围最近邻原子;Ri表示中心原子到一对最近邻原子的距离。计算所得不同结构的CSP取值及其在图4、图6、图10的对应颜色标注如表5所示。

表5 不同晶体结构CSP取值及其对应颜色
图4给出了vc=20 m/s“V”型位错环、梯杆位错、堆垛层错四面体SFT、棱柱位错缺陷、点缺陷和原子团簇在工件内部的位置,采用中心对称参数法CSP作图。为了更好的显示缺陷的原子结构,图5a)、图5b)给出了堆垛层错四面体SFT、原子团簇局部放大图。刀具不断前进,切削区工件原子被迫移动,此时部分原子脱离原来的晶体位置,并不断运动形成间隙原子。间隙原子在工件的内应力作用下相互吸引并逐渐聚集,形成了图5b)所示的原子团簇结构。
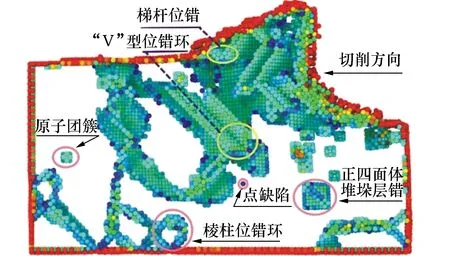
图4 工件内部位错与层错等缺陷分布
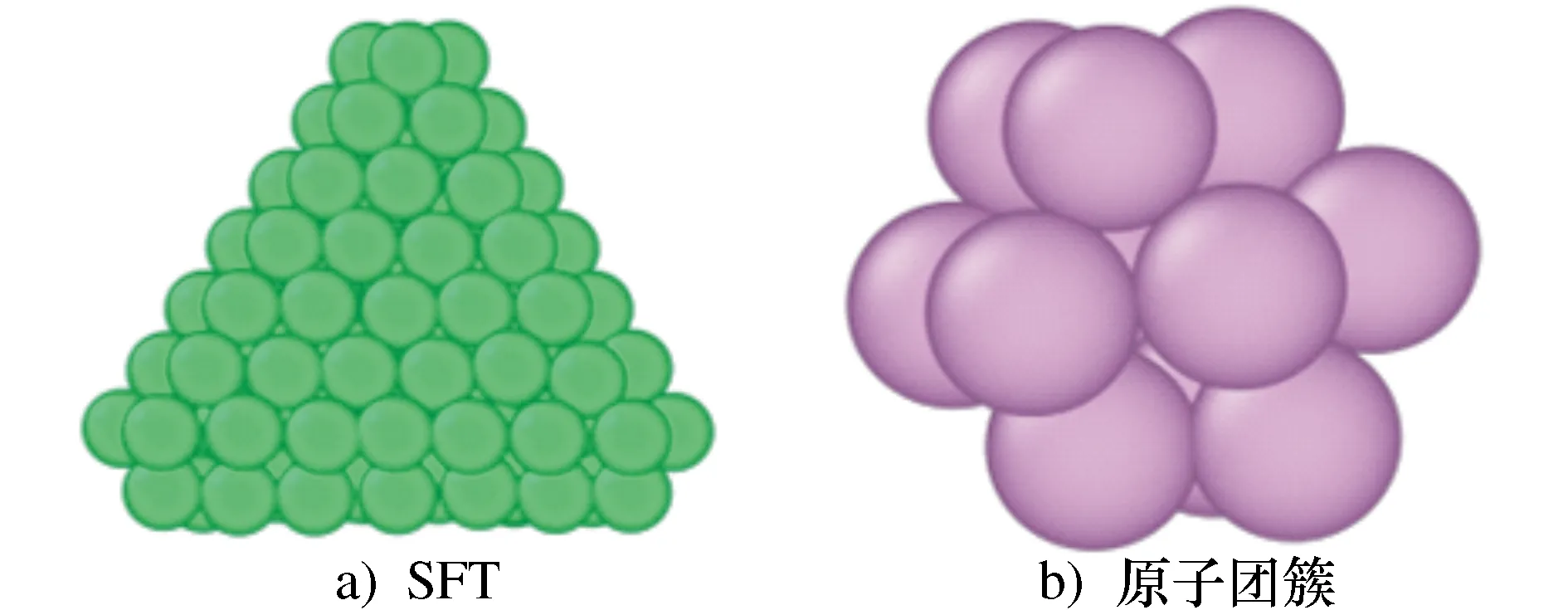
图5 亚表面缺陷局部放大
图6采用CSP与DXA方法描述切削过程堆垛层错四面体(SFT)演化过程,图6a)与图6d)的切削距离为4.8 nm,图6b)与图6c)的切削距离为5.2 nm,图6c)与图6f)的切削距离为5.6 nm。图6a)、图6b)、图6c)中采用CSP方法作图,洋红色表示标记的SFT原子,为了有更好地显示效果,去掉CSP<2的原子;图6d)、图6e)、图6f)中采用DXA方法作图,深蓝色表示完美位错,绿色表示肖克莱位错,紫色表示stair-rod位错,浅蓝色表示Frank位错。
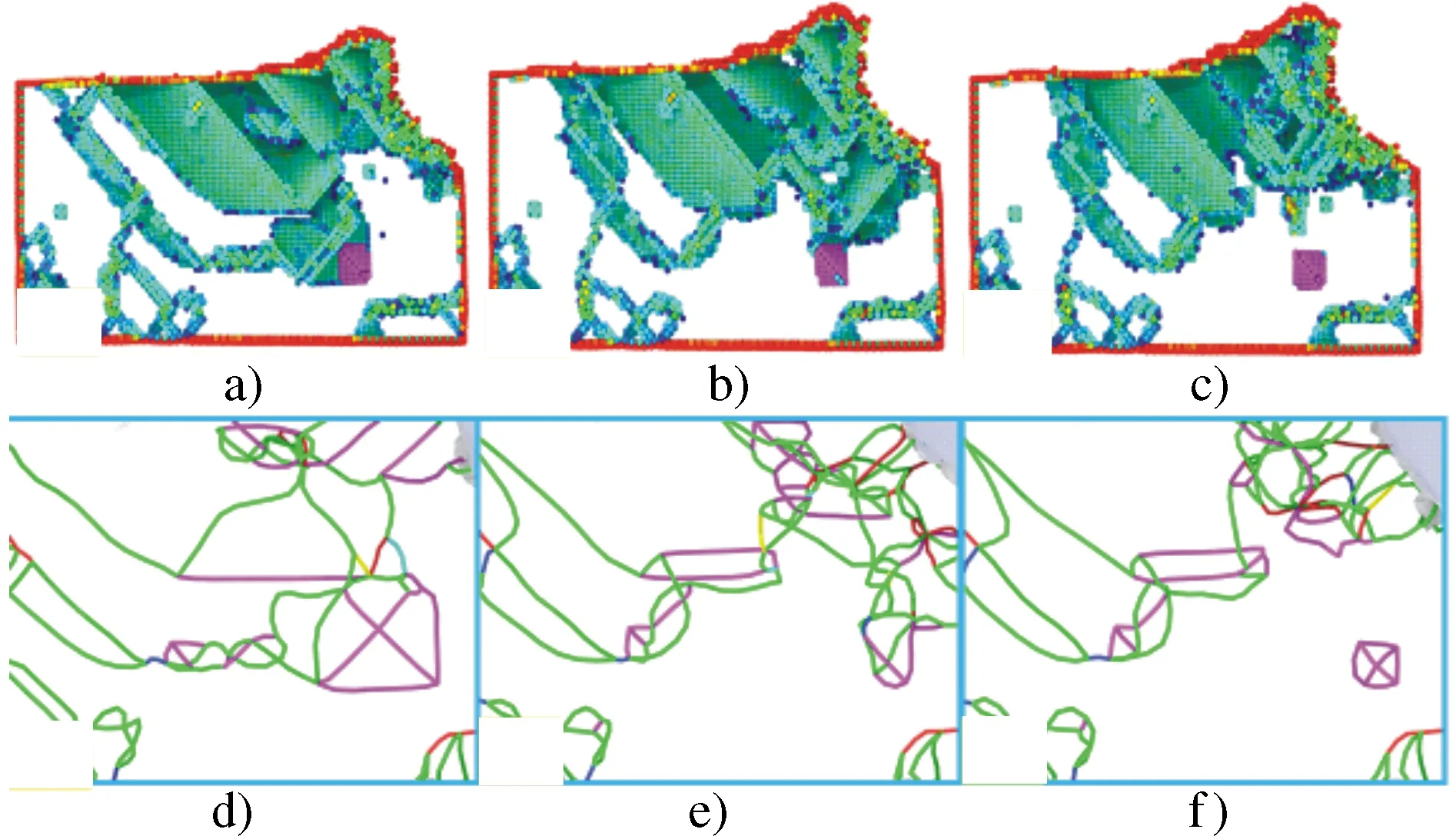
图6 采用CSP与DXA方法描述切削过程堆垛层错四面体演化过程图
采用CSP和DXA位错提取算法[28]对仿真结果进行可视化,将SFT原子放在一组并标记为洋红色,结合图6a)CSP分析与图6d)中DXA分析可以发现,在图6d)中存在2条与梯杆位错并存的肖克莱位错时,SFT形成了除底面之外的3个表面。从图6e)中发现肖克莱位错在切削过程中不断运动,并与梯杆位错和深蓝色的完美位错交叉,不运动的梯杆位错锁留在原位置。肖克莱位错取代梯杆位错与SFT相连接。图6b)中显示此时SFT处于悬挂位置(即将形成)。从图6c)与图6f)中可以发现,肖克莱位错不断运动并与梯杆位错发生分离[29],使得梯杆位错独立出来,形成了完整的堆垛层错四面体。CSP分析与DXA的分析表明:SFT形成过程中释放大量能量,并与其他缺陷结构分离,逐渐开始形成相对稳定的缺陷结构。Lu等利用高分辨率透射电子显微镜(TEM)获得了Ni-Fe单晶合金微观SFT演化过程的图像如图7所示[30]。
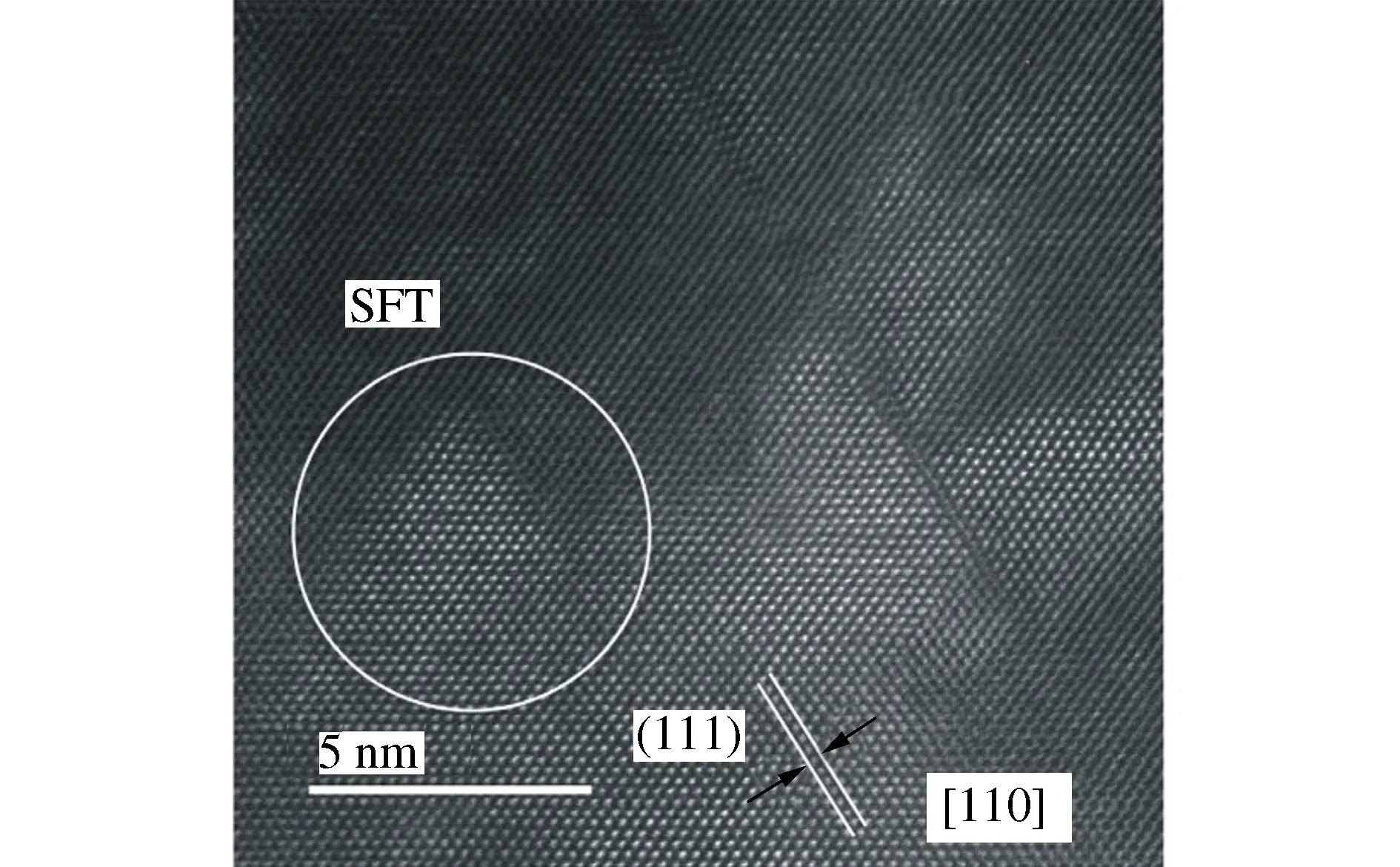
图7 高分辨率透射电子显微镜获得的单晶Ni-Fe合金堆垛层错四面体图像[30]
实验过程得到的SFT微观结构图像与仿真结果基本匹配,间接证明分子动力学仿真的正确性。
图8和图9分别显示了“V”型位错和梯杆位错局部放大图和形成原理图。

图8 “V”型位错局部放大图和形成原理图
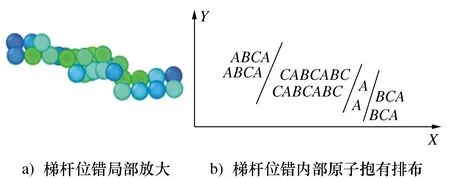
图9 梯杆位错局部放大图和形成原理图
“V”形位错环的形成与演化对切削过程中亚表面质量有着重要影响。切削过程中,刀具对工件产生了极高的挤压力,使得工件这些缺陷结构主要分布在加工区域下方,位错环表示一些内部形核的位错由于没有足够的能量扩展到工件表面而形成的封闭环。图8a)给出“V”型位错局部放大图。“V”形位错由两个X1与X2肖克莱位错和梯杆位错组成。首先,X1与X2位错在C点与D点形核,X1与X2位错沿着伯格斯矢量方向做滑移与扩展运动,在扩展运动中发生交叉滑移。沿[110]方向扩展的位错到达表层后停止,在图8b)上表面沿[1-11]或[11-1]留下位错线。当两个位错向下运动时,在节点A相交并发生干涉,共同形成了阻碍位错滑移的位错锁。梯杆位错B在A节点开始形核,并沿[1-11]方向扩展,不断运动形成了梯杆位错。梯杆位错阻碍肖克莱位错继续滑移,两个肖克莱位错和沿着侧面扩展的梯杆位错以及层错共同组成“V”型位错组态。
梯杆位错(SRD)是工件被切削后亚表面内部形成的缺陷结构。图9a)是切削过程形成的局部梯杆位错放大图,图9b)图给出了梯杆位错的原子排布图。局部放大图可以发现梯杆位错的两层原子发生错动,中间原子在扩展过程中发生迁移,位错与其他缺陷的在扩展运动中发生竞争导致原子错排,最终形成了具有2个阶梯的梯杆位错。
3 切削速度对亚表面损伤的影响
在切削过程中,切削速度对工件的表面形成,切屑的运动,工件内部中各种缺陷的形核和演化和表面质量有着重要的影响。这些演化会直接地影响工件亚表面晶体结构,缺陷演化,亚表面厚度,进而会影响表面的质量。图10给出了3组不同的切削速度,分别是20 m/s,16 m/s,12 m/s,采用中心对称参数表征的亚表面缺陷瞬态图像,并比较了亚表面缺陷数量,黑色框选区域代表亚表面缺陷的面积与深度。

图10 s=15 nm,切削速度不同时,工件亚表面缺陷与晶体结构的变化
切削过程中,工件内部缺陷与亚表面晶体缺陷是由于位错的形核、扩展运动而形成的。刀具-工件接触区域发生剧烈的剪切与挤压作用,接触区域附近的工件原子产生较大的迁移。其中亚表面原子迁移距离较大,未加工区域原子迁移距离较小。
在速度为12 m/s时,从图10a)可以发现工件亚表面的缺陷数目很多,而且缺陷面积很大;随着切削速度逐渐增加,亚表面各种层错的面积和数目出现了明显的减少,位错的种类也明显减少。出现上述现象的原因是:在切削速度较低时,切削相同距离下,切削时间较长,亚表面的缺陷有着充分的时间与足够的能量进行位错的形核,滑移与湮灭,长时间应力驱动[31]使得位错可以扩展到深层,位错形核后得到充分扩展。各种位错发生相互交叉与干涉,新的位错开始出现,使得亚表面缺陷的种类增加。增大切削速度后,切削相同距离刀具对工件的切削时间较为短暂,工件内部位错的形核无法充分滑移,因此加工面的各种缺陷的面积和数目大为减少。随着切削距离增加,切削产生的应力持续驱动位错的滑移与湮灭,因此亚表面的层错与位错的面积逐渐减少。
亚表面的深度[32]计算式为
H=10a-d-y
(6)
式中:d是切削深度;y是工件内部未发生缺陷区域的y坐标。容易发现,亚表面的深度不随切削速度的变化而发生改变。图10也得到了与公式(6)计算相同的结果。
根据图11得到3组不同速度下,原子势能随切削距离的变化。初始切削时,势能出现上升过程,由于刀具切入工件后,合金原子受到剪切应力与挤压应力作用,原子势能增加,能量增加导致原子大量迁移。随着切削距离增加,发现位错的形核、扩展和湮灭的过程伴随着位错的合并与分解,是不断消耗能量的过程。3种不同的速度得到了相同的结果,镍铁铬合金中晶体的位错形核与扩展应克服高能势垒,此时会导致能量的波动,势能的波动代表着原子位置的迁移时原子之间相互作用的变化,切削区的原子迁移后,周围原子通过调整位置降低体系势能。图11中势能不断降低,并逐渐趋于平稳,原子的迁移变化减小。
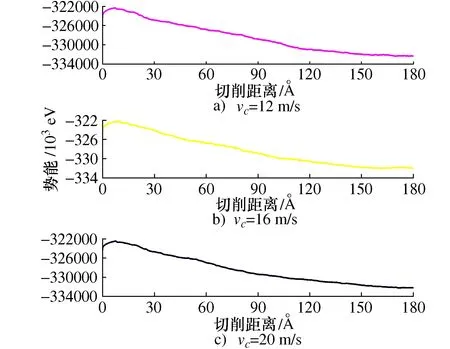
图11 不同切削速度下,原子势能随切削距离的变化图
图12给出了3种不同速度下动能随切削距离的变化。
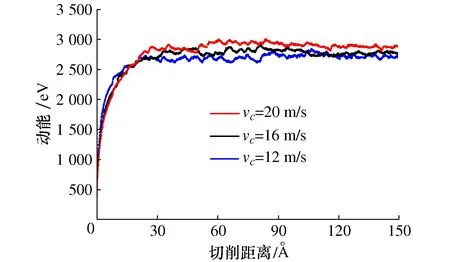
图12 动能随切削速度的变化
可以发现动能随切削速度的提高而增大,最后动能趋于平稳;初始切削时,刀具克服工件的切削阻力做功,在局部接触区域大量原子发生位移,原子之间斥力很大;切削3 nm以后,原子运动达到平衡态,阻力减小,只需要一定的切削力提供刀具前进的动力,因此动能趋于平稳;动能随速度增加而逐渐变大,使得更容易克服位错发射的势垒。总能量为势能与动能的和,容易发现总能量是降低的过程,这表明系统是逐渐趋于最稳定状态。


(7)
式中:l为位错线的总长度;V为切削区域的体积。
图13给出了3种不同切削速度下,位错密度随着切削距离变化的曲线。
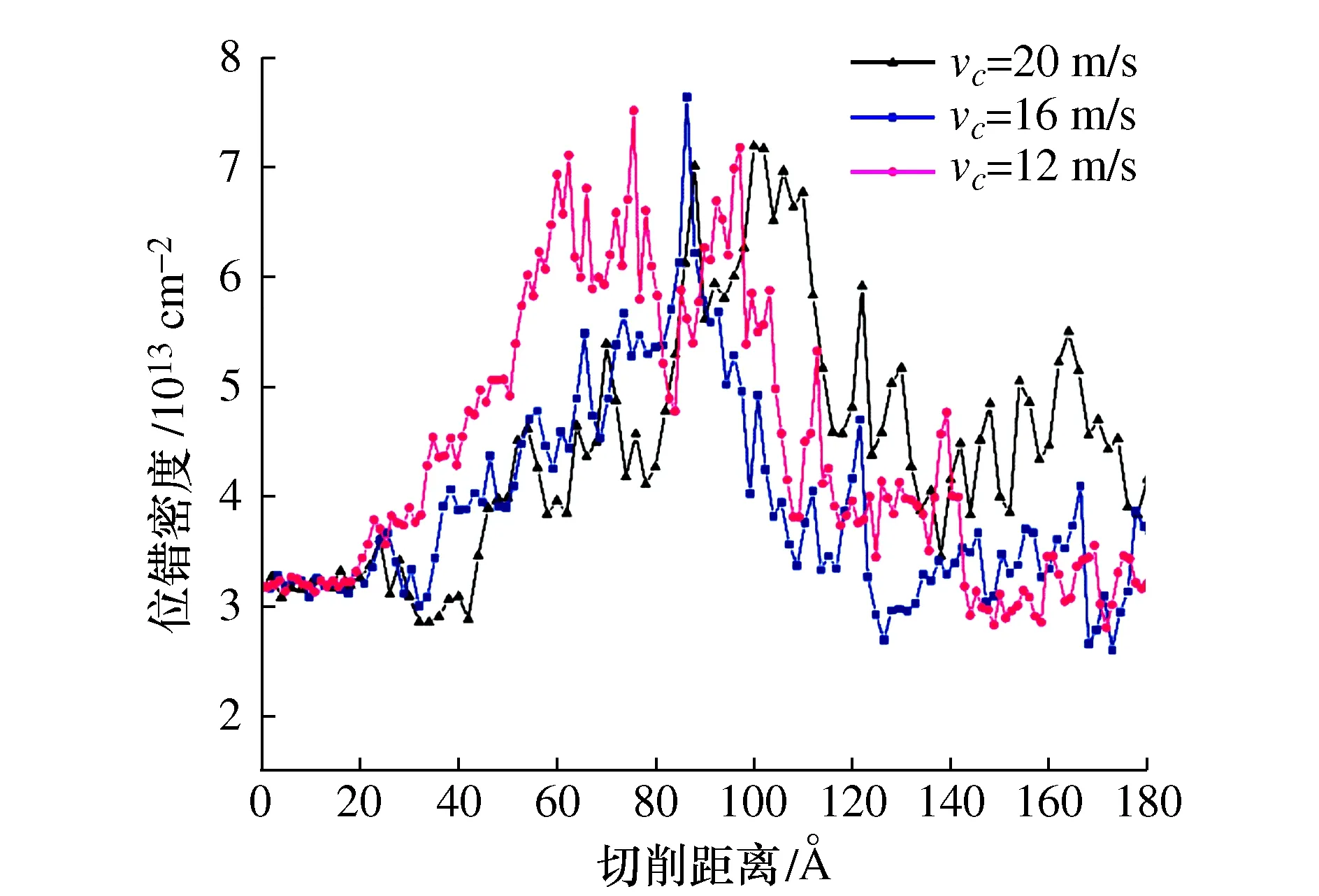
图13 位错密度随切削距离的变化图
在s<5 nm时,切削速度越低,产生的位错密度越大。在初始切削时,速度越快,产生的温度越高,位错的扩展随之加快。位错的湮灭随温度升高加剧,因此出现当初始阶段位错密度随切削速度增加而降低。切削产生形变量随着切削速度提高而增大,金属的塑性变形抗力随之增加,其硬度和强度明显增加,此时位错密度也会增加,出现加工硬化现象。可以发现前半部分(第一阶段)是温度机制起主要作用,后半部分(第二阶段)是加工硬化对位错密度影响起主要作用。
图14给出了在不同切削速度下切削力的变化。
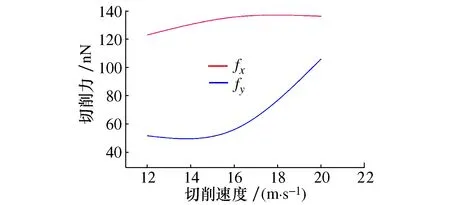
图14 切削力随不同切削速度的变化
可以看出,切削力的变化反映了刀具与工件作用以及材料切削去除过程,是表征刀具与工件作用的重要参数。切削力由切削过程的摩擦阻力和被去除材料的抗力组成。可以发现,主切削力fx随切削速度增加而逐渐增大。
研究切削力以后,同时测量了前刀面与滑动切屑之间的摩擦因数μ[33-34],摩擦因数μ计算式为
(8)
式中:Fx为平均切削力;Fy为沿y方向的平均推力;刀具前角γ0=15°,
从图15可以发现摩擦因数随切削速度的增加而不断增大,切削速度越快,相同时间切屑产生的量越大,刀具与工件之间的相互作用就越大,因此摩擦因数也不断增加。

图15 摩擦因数随不同切削速度的变化
切屑的厚度h采用
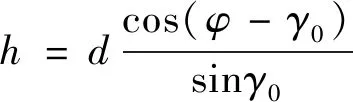
(9)
剪切角φ表达式为[34]

(10)
式中β为摩擦角,tanβ=μ。仿真得到的切屑厚度如表6所示。

表6 不同速度下切屑厚度变化
切削速度越大,单位时间切削距离越大,材料的去除率越高,形变量越大,因此形成的切屑厚度越大。
在图16中对切削过程中晶体结构演化进行了分析,图16a)显示了FCC原子的数量随着切削距离增加不断减小,而且速度越高,转化为其他结构的速度越快。图16b)给出了HCP原子(位错、层错等缺陷的主要组成结构)数量的变化趋势,HCP原子数目随着切削距离而增加,表明切削过程中不断有缺陷产生,缺陷面积不断增加;速度越高,HCP原子的数目越少,表明在速度较高时,亚表面缺陷的面积较小。
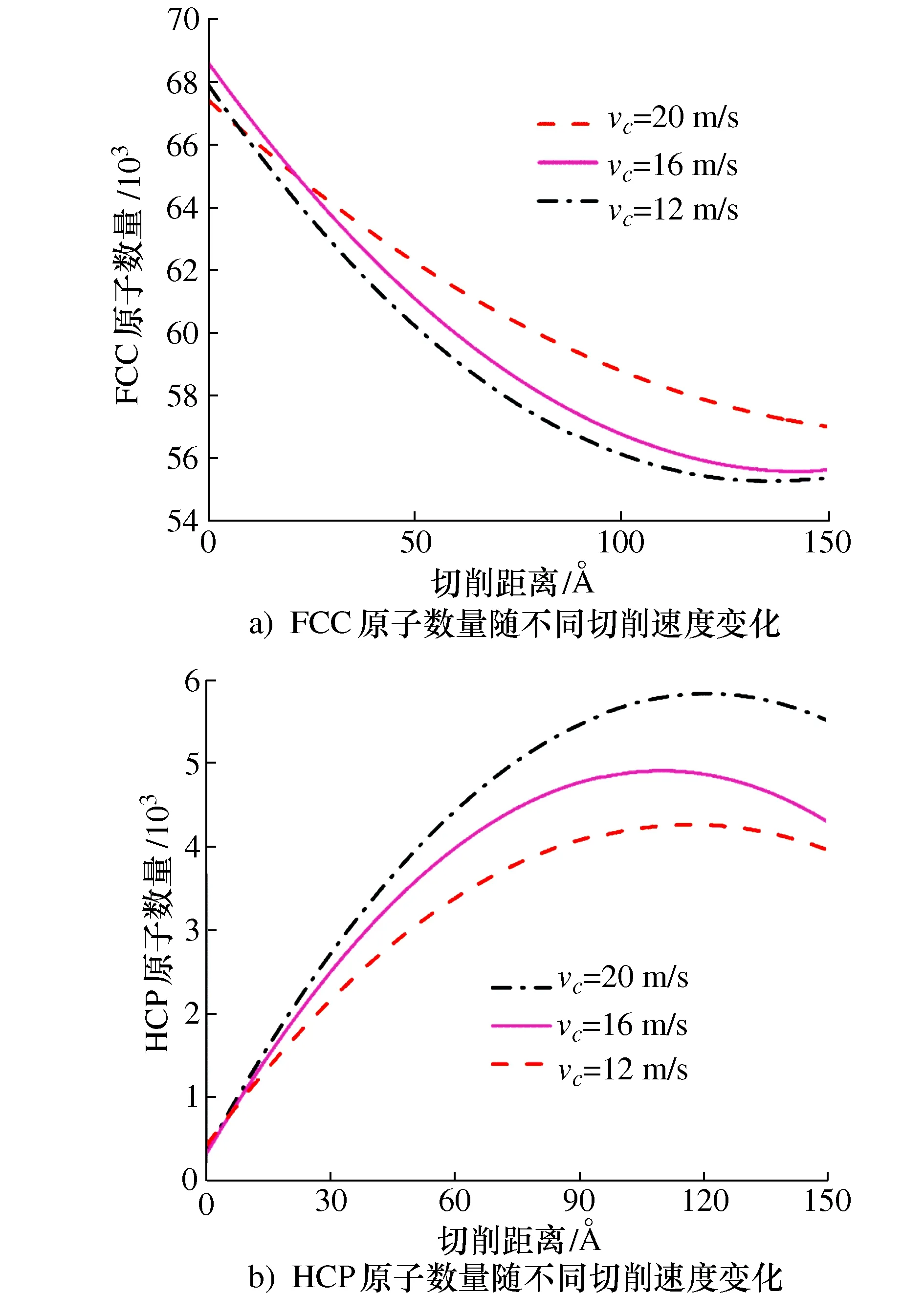
图16 FCC、HCP原子数目随切削速度的变化图
4 结论
采用分子动力学(MD)的方法对氮化硅刀具切削镍基单晶合金的加工过程亚表面缺陷演化进行了研究。建立了综合性能优异的氮化硅刀具切削镍基单晶合金模型,并开展了关于切削过程中出现各种亚表面缺陷的细致研究,从多个角度研究了不同切削速度对亚表面缺陷演化机制的影响。得到如下结论:
1) 切削过程中形成了原子团簇、堆垛层错四面体、V型位错环和梯杆位错,棱柱位错等缺陷。利用CSP和DXA等先进算法对4种典型缺陷的形核与演化进行深入分析,揭示了缺陷演化机理;通过MD仿真结果与实验结果对比,证明仿真结论的正确性。
2) 提高切削速度使得亚表面中各种缺陷的数量以及种类明显减少,切削速度变化对亚表面缺陷深度没有影响。
3) 能量分析表明切削过程中能量随切削距离增加而降低;对位错密度进行分析,发现切削第一阶段位错密度与切削温度速度成正比关系,第二阶段加工硬化对位错密度起主要作用;通过分析晶体结构变化,发现切削速度越低,缺陷的面积越大。
4) 综合分析可知提高切削速度有利于减少亚表面缺陷,提高镍基单晶合金零件表面质量。
