混沌区间多目标粒子群优化算法及其应用
2022-07-18李俊李济顺HALGurgenci李伦GUANZhiqiang杨芳
李俊,李济顺*,,HAL Gurgenci,李伦,GUAN Zhiqiang,杨芳
(1.河南科技大学 机电工程学院,河南洛阳 471003;2.河南科技大学 河南省机械设计及传动系统重点实验室,河南洛阳 471003;3.University of Queensland,School of Mechanical and Mining Engineering,Brisbane QLD4072,Australia)
超临界二氧化碳(sCO2)循环介质与传统的蒸汽介质相比具有高温下腐蚀性小,所需压缩功少,热效率高等优点。因此sCO2布雷顿循环被认为是下一代应用于包括核能、化石燃料和集中太阳能发电的技术[1-3]。为了解决高温下发电机转子系统散热问题,引入了sCO2气体冷却装置。冷却装置同时具有辅助支承转子叶轮悬臂和散热的作用。为了避免冷却装置的刚度为转子的动力学特性带来负面影响,同时提升转子系统动态性能,本文基于转子动力学对轴系的相关参数进行全面的优化设计。
轴系的优化模型是工程中典型的多目标优化问题,各个目标函数可能是相互冲突的,通常只能得到全局非劣最优解或次优解,这为传统数值优化算法的应用带来了挑战。为了解决多目标优化问题,包括多尺度量子谐振算法[4]、多目标遗传法[5]、仿生粒子群算法[6]等智能优化算法相继被用在实际工程上。李超等[7]基于试验应用多目标遗传算法对某航空发动机轴系的初始结构布局进行了优化设计,并论证了优化的结构布局可以提升转子的动力学特性。张微等[8]综合转子动力学特性与阻尼器相关参数,应用胞映射方法对挤压油膜阻尼器的弹簧刚度和油膜间隙进行多目标优化设计,并得到了Pareto最优解集。为了充分考虑风力发电机叶片气动特性与其结构性能之间的耦合效应,Wang等[9]提出了一种多目标形状拓扑耦合优化方法,同时优化了转子叶片的外形和内部结构布局。Ramanujam等[10]以直升机旋翼为基线构型,通过多变量粒子群优化技术在转子动力学分析中的应用,以实现变速变几何转子系统输出功率最小化。Xu等[11]将RBF神经网络、径向基函数和进化算法相结合,提出了一种考虑支承刚度不确定性的转子系统动态响应优化设计方法。
Lu等[12]利用粒子群优化算法和支持向量机,在任意载荷下确定空间钢构架的测量响应和估计响应之间的映射关系。Mijbas等[13]采用混沌粒子群(CPSO)算法优化后的阻尼控制器对电力系统稳定器(PSS)和PID进行增强,从而抑制单机无穷大系统的低频振荡,取得了较好的控制效果。Norsahperi等[14]研究了基于分数阶神经基(NNFOPID)和粒子群(PSOFOPID)的双旋翼气动系统的变桨距控制方法,并实验验证了两种控制器的鲁棒性和低功耗特性。Nowak等[15]采用响应面-遗传(RSM-GA)算法结合有限元技术对汽轮机的启动曲线进行了优化,使汽轮机整个启动过程所用的时间不到优化前的一半。Bernardini等[16]将二元遗传优化算法用于识别直升机前飞旋翼的叶片形状和结构特性等设计参数。
以上的研究成果表明,群体智能技术在工程优化、参数识别和控制等领域得到广泛的应用。对于高速轴系优化工作所面临的主要问题包括两个方面。首先,转子的工作转速可能包含或跨越多个临界转速,并且要求不平衡响应限制在安全和可以被接受的水平。其次,冷却装置的刚度是非线性的而且随着转子的转速改变而变化,因此冷却装置的刚度是一个非线性的二维矩阵。针对这两个问题本文提出了混沌区间多目标粒子群优化(CIMPSO)算法,并对工作转速为5.0×104r/min,功率为300 kW超临界二氧化碳微型透平机的轴系相关参数进行了优化设计。
1 微型透平机优化问题
1.1 微型透平机主轴系统基本结构
在图1所示的透平机转子系统结构中,S1、S2和S3分别是叶轮、冷却装置和密封机构轴向尺寸,S1=2D,S2=S3=D;冷却装置的介质采用超临界二氧化碳气体。
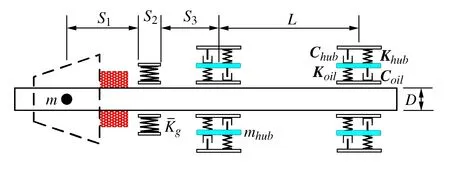
图1 微型透平机转子示意图
相距为L的主要支承的复合刚度可以采用串联刚度阻尼系统的表达式[17]来计算,即
(1)
对于采用柔性轴承座的可倾瓦轴承结构,Koil和Coil分别为轴承的刚度矩阵和阻尼矩阵,关于Koil和Coil的计算方法在参考文献[18]中有详细的介绍,这里不再赘述。Khub和Chub分别为轴承座的刚度和阻尼矩阵。转子的涡动频率表示为复数,即
A=iω
(2)
若转子的直径为D,定义轴承间距为
L=bD
(3)
式中b为待优化系数。作为辅助支承其刚度是转子转速和转子位移的非线性函数,可以表示为
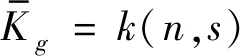
(4)
为了建立有限元模型和传递矩阵模型,叶轮被等效为直径d=100 mm,厚度h=10 mm的刚性圆盘,其质量为0.71 kg。此时圆盘和叶轮具有相同的直径转动惯量和极转动惯量。若叶轮的平衡等级按照汽轮机转子标准取G2.5级[17],转子的工作转速(即工频)为nwork,则其残余质量最大偏心距e=75/(πnwork)。
1.2 转子系统优化目标函数
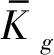
(5)
式中:输出参数ei和fi为分别表示复振型和截面的内力(弯矩和剪力);u为盘轴单元对应的传递矩阵,关于传递矩阵的详细介绍可以参考文献[17]。转子系统设计是一个多目标优化问题,可以作为适应度评价函数有
1) 残余质量的不平衡响应最大的峰值
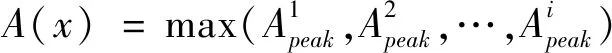
(6)

2) 距离工作转速最近的临界转速与工作转速(工频)之间的差值
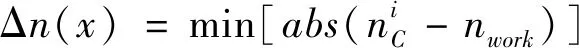
(7)
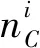
3) 工频点处不平衡响应幅值变化率
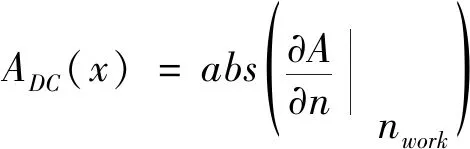
(8)
在实际数值计算中可以写成差分形式
(9)
式中:An+1和An-1分别表示与工频点相邻的转速点处的不平衡响应的幅值,同样可以由复振型ei求得。Δn为扫频间隔。则其约束优化数学模型可以写为
f(x)=f(A(x),Δn(x),ADC(x))
(10)
由于多个目标函数可能相互冲突,而且目标函数值并不在同一数量级,因此种群的适应度值的计算可以采用各函数的曼哈顿距离加权求和(MMD)的方式。上述A(x)的作用是抑制转子的共振幅值,而Δn和ADC(x)的作用是使工频远离共振频率且确保转子运行在稳态涡动区。
1.3 约束空间
为输出部件预留一定的空间的同时保证转子的刚度,因此参数b的约束范围是
3≤b≤6
(11)
轴承座的相关参数约束范围取
(12)
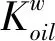
(13)
式中:Kupper为工程实际应用中冷却装置刚度的上限,由润滑介质压强,冷却装置的结构参数所决定。对于轴系来说,每一次扫频分析,输入系统的冷却装置刚度都是一个与转速和转子位移有关二维矩阵。由于气膜刚度的非线性,在数值分析的过程中冷却装置的刚度是未知的。这为常规的遗传算法、模拟退火算法和粒子群算法等在轴系中优化的应用带来了挑战。针对该问题,本文提出基于粒子群的混沌区间多目标优化算法(CIMPSO),并对一种超临界二氧化碳太阳能微型透平机的转子系统进行了优化设计。在上述冷却装置刚度约束范围内取特征数Kge作为粒子向量中的一个元素,则待优化的粒子向量可被描述为
(14)
2 转子系统优化方法
2.1 标准粒子群优化算法
基本粒子群优化(Particle swarm optimization,PSO)计算方法是一种基于自我认知和社会心理学的计算技术。在寻优空间中的每一个潜在可行解都被抽象为个体粒子(Particle)向量xi。粒子群算法首先在约束空间中随机初始种群,每个粒子由速度和位移进行定义。在搜索空间中个体粒子在局部寻优的同时实现信息共享机制。粒子正确的行为得到加强,同时被其他粒子所模仿,最终收敛到最优解或者非劣最优目标域(Pareto front)。
标准粒子群优化算法迭代更新粒子[6]的表达式为:
vi(t+1)=wvvi(t)+c1r1[pi(t)-xi(t)]+
c2r2[pg(t)-xi(t)]
(15)
xi(t+1)=wxxi(t)+vi(t+1)
(16)
设初始化粒子的个数为N,i=1,2…,N,表示粒子的编号。每个粒子由目标函数f(x)决定其适应度。在迭代过程中各个粒子记忆、追踪当前个体最优粒子pi(t)和全局最优粒子pg(t)。wv和wx为惯性权重,进一步决定了算法的局部和全局寻优能力。r1、r2取0到1区间的随机数,表示粒子的认知能力。c1、c2为学习因子,表示学习能力。
2.2 混沌区间多目标粒子群模型
非线性粒子指得是每个粒子中的若干元素是一个二维非线性变化的元素。对于本文轴系来说冷却装置的刚度是一个根据转轴转速和位移变化的参数。粒子中非线性元素的取值受到工程应用的约束。设约束的上限和下限分别为:
(17)
式中:α和β是基于粒子元素特征数的拓展系数。为了实现含有非线性元素的粒子群寻优,这里引入混沌变量。由典型的混沌系统Logistic方程[6],可以得到具有随机性的混沌变量。混沌变量在一定范围内体现规律性、遍历性和随机性。
zn+1=μzn(1-zn)n=1,2,…,N
(18)
式中:μ为控制参量;zn∈[0,1]。每一迭代步对粒子xi更新后,将冷却装置刚度特征数Kge映射到Logistic方程,进行混沌变量初始化
(19)
式中t表示当前迭代步。将z1(t)代入Logistic方程进行迭代产生混沌变量数列zi+1(t)(i=1,2,…,N)。把混沌变量数列zi+1(t)逆映射到求解空间中得到
(20)
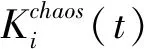
(21)
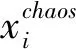
pg(t)=comfit[pi(t)]
(22)
式中comfit(·)指的是当前迭代步综合目标函数最优的粒子。每个粒子的子目标函数的归一化为:
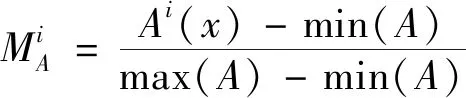
(23)
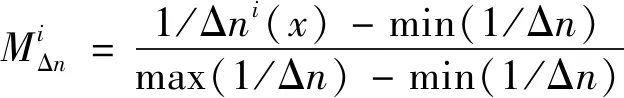
(24)
通过加权的方式得到每个个体粒子的综合目标函数值为
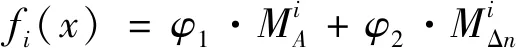
(25)

(26)
(27)
而当前迭代步中被替换后的粒子中刚度特征数元素任然采用Kge(t)。最后按照标准粒子群算法式(15)和式(16)迭代得到新粒子
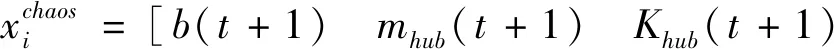
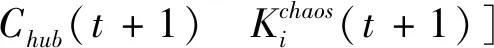
(28)
上文所描述的算法称为混沌区间多目标粒子群优化算法(Chaos interval multi-objective particle swarm optimization algorithm,CIMPSO)。与标准混沌粒子群优化算法(Chaos particle swarm optimization,ChPSO)相比,本文提出的CIMPSO可以对多目标和含有二维非线性元素的粒子群模型进行空间寻优计算。当个体最优粒子和全局最优粒子不在随迭代步进化,此时粒子群的各个粒子独立更新,最终所有粒子趋于全局最优解或者非劣最优解。而粒子群中所有粒子都包含有二维非线性元素特征数的混沌映射,这就保证了在映射区间范围内二维非线性元素的区间得到有效的空间寻优计算。
2.3 CIMPSO算法归纳和收敛性分析
CIMPSO的主要优势在于解决含有非线性、二维变化的元素的多目标优化问题。算法主要分为以下几个步骤。
步骤1 初始化相关参数,包括学习因子c1、c2,粒子群规模N,寻优次数T,速度惯性权重wv和位置遗忘惯性权重wx,拓展系数α和β,控制参量μ,加权系数φ1,φ2,…,φN。在约束范围内随机初始化粒子群中的所有粒子位置。
步骤2 粒子位置记为xi(t)。确定粒子群非线性元素的特征数xi(t,j)(j表示粒子向量中非线性元素的位置编号,t表示迭代步数)。将特征数映射迭代产生混沌变量序列
(29)
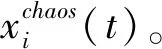
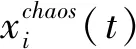
(30)
用MMD算法计算当前层级中粒子的每个目标函数的Manhattan距离Mi。由加权的方式得到每个粒子的综合适应度
fi(x)=φ1M1+φ2M2+…+φkMk
(31)
则全局最优解即为综合目标函数的极值所对应的粒子。
pg(t)=comfit[Pi(t)]
(32)
步骤4 生成混沌变量序列
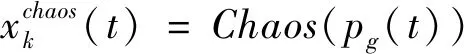
(33)
Zitzler提出的ZDT问题是常用的两目标测试函数[19]。本文选取ZDT1和ZDT2作为被测对象:
f1(x)=x1
(34)
f2(x)=g(x)[1-(f1(x)/g(x))m]
(35)
xi∈[0,1],i=1,2,…n;n=30
(36)
当m=1/2时上式为ZDT1(凸函数),当m=2时为ZDT2(凹函数)。它们的理想Pareto前沿端已经被给出,如图2中的点划线和虚线所示。元素x1同时影响两个目标函数,因此被选为特征数元素。图中的蓝色短线段为数值实验所得到的解区间。对应的初始化粒子个数为50,迭代步数为200步,寻优计算次数为200次。从图中与理想Pareto前沿对比可以明显看出实验解以一定的误差范围收敛于非劣最优解(PFtrue)。其中ZDT1和ZDT2的测试解(EXPERIMENT)的平均误差分别为e1=16.1%和e2=11.69%。
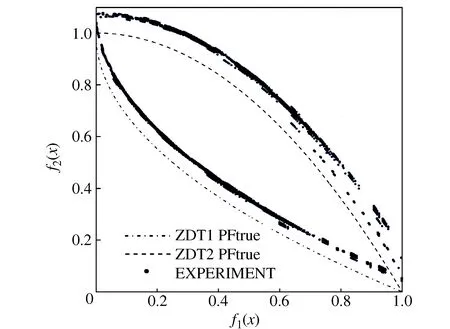
图2 理想Pareto前沿(PFtrue)和测试解集(EXPERIMENT)
3 转子系统模型寻优计算
如上文所述超临界二氧化碳透平机转子系统待优化参数包括主要支承系统轴承间距L=bD,轴承座质量mhub、刚度Khub和阻尼Chub,冷却冷却装置的刚度Kg。其中Kg是转子转速和位移的函数,其特征数取Kge。各元素约束条件为
(37)
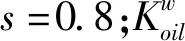

表1 粒子群模型参数
表1中参数的取值范围均在0~1之间,其中拓展系数、控制参量以及曼哈顿权值均由决策者根据具体的优化问题的侧重点自行设定。学习因子c1和c2分别影响算法的局部搜索和全局搜索能力,为了避免寻优过程陷入局部极值和提高收敛的精度,c1和c2均取中间偏大值0.6。惯性权重wv和wx是用来进一步平衡局部寻优和全局寻优之间的矛盾,在算法完成后通过测试调整惯性权重的大小。
按照设计经验,轴承的间距取轴径的3~5倍,这里取3;轴承座的参振质量取转子质量(2.49 kg)的一半,即1.2 kg;轴承座的刚度取可倾瓦轴承刚度的二分之一,阻尼取可倾瓦轴承的阻尼系数;冷却装置的刚度任取约束空间的中间值。则经验粒子参数为
(38)
图3所示的点划线表示的是在该参数下转子系统的不平衡响应。
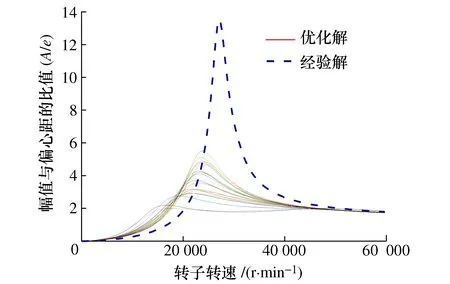
图3 挠性轴承座可倾瓦轴承转子系统优化设计前后转子不平衡响应
由图3可知优化前相对峰值为13.51-2.0=11.51。在约束空间内随机初始化粒子,连续寻优计算25次,分别将25组非劣最优解带入转子系统所产生的不平衡响应如图中实线所示。与点划线相比,实线表现出的最小峰值衰减率为69.6%,且转子的响应曲线更加平缓,体现了CIMPSO算法的鲁棒性。工作转速(nwork=5.0×104r/min)与距离最近的临界转速的差值约占工作转速的30%,保证了转子工作在平滑的稳态涡动区。
柔性转子系统的临界转速和不平衡响应与轴承的特性密切相关,为了验证算法可以适用于不同的转子系统,现对主动磁悬浮(AMB)轴系进行优化计算。AMB轴系的待优化参数为轴承间距bD和冷却装置的刚度kcb,与挠性轴承座可倾瓦轴系相比可以优化的元素较少,且在所研究的频率范围内,AMB轴系出现了悬臂主导的多个模态频率。图4为 AMB支撑的微型透平机优化前后叶轮的频响曲线图。磁悬浮轴承的刚度和阻尼分别为kAMB=8.2×105N/m、CAMB=100 Nm/s。图中实线和虚线分别为多次寻优计算得到的Pareto前端和优化前的经验粒子xe所确定的谐响应曲线。与虚线相比,实线的最大幅值有了明显的衰减。另一方面,随着模态频率向低频方向移动,部分优化解使得工频范围内悬臂的模态频率削减为单个。
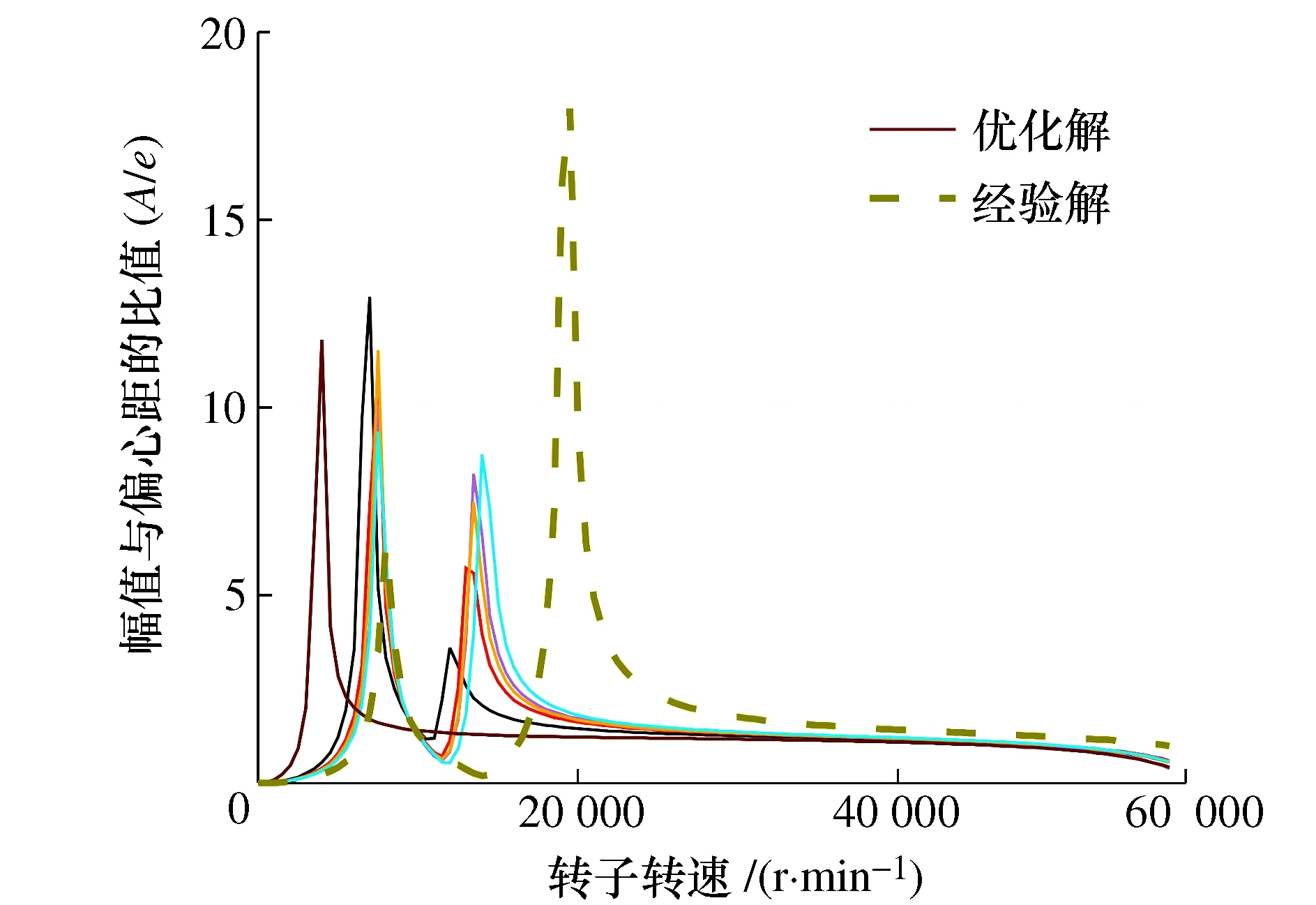
图4 主动磁悬浮轴承转子系统优化设计前后转子不平衡响应
任取数值计算所得的非劣优化解,即
x=[3.8 1.6 1.01×1085.05×1042.43×105]
(39)
特征数x(5)所对应的冷却装置的刚度变化范围是Kg=[Kge(1-α),Kge(1+β)]。为了直观分析算法的收敛过程,令全局适应度为
f=1/A(x)+Δn(x)
(40)
该组优化解的收敛过程如图5所示。由图可知,全局适应度在算例迭代110步后稳定。
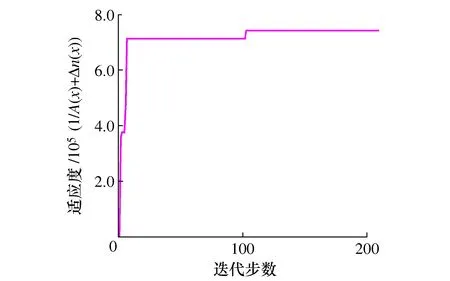
图5 CIMPSO算法的收敛性
图6中的实线和虚线分别表示目标函数A(x)/e和Δn(x)随着迭代计算的收敛过程。由曲线的变化趋势可知,目标函数A(x)和Δn(x)是相互冲突的,虚线位置向下波动的同时实线必然相对向上波动。整个优化过程伴随着A(x)和Δn(x)之间的博弈。最终全局收敛时,虚线所代表的目标函数Δn(x)妥协,适量增加以换取峰值目标函数A(x)的减小。再一次证明了CIMPSO算法对有冲突的多目标转子优化问题可以进行有效的寻优计算。
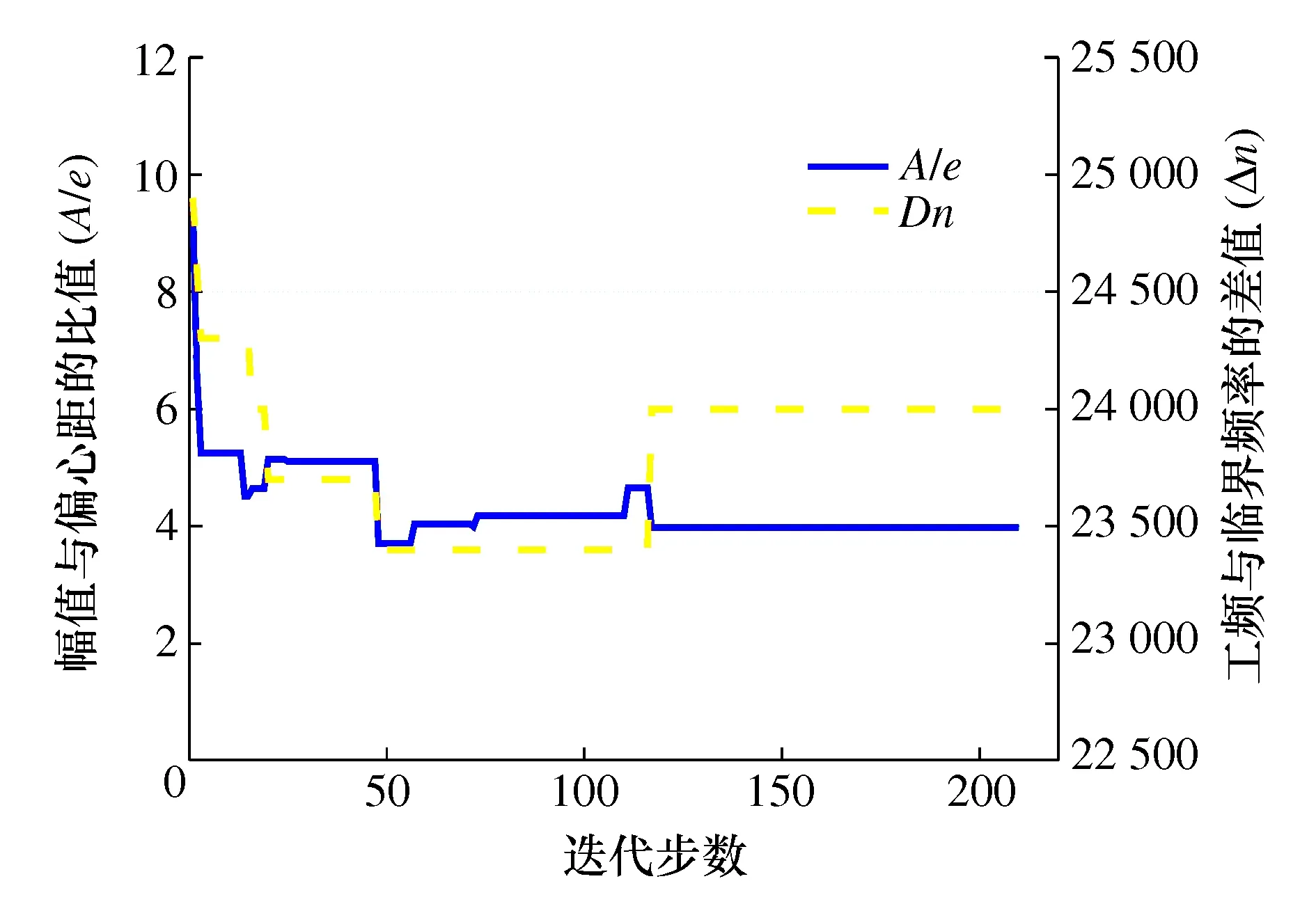
图6 子目标函数变化趋势
4 仿真验证
传递矩阵法的计算精度取决于转子被分成盘轴单元的数量。盘轴单元数愈多计算精度越高,但是累积的数值误差越大。本节以转子谐响应为目标建立其有限元模型,对优化结果进行对比验证。如图7所示,在有限元三维模型中叶轮等效为相同质量、转动惯量的质量点。柔性轴承座有效参振质量为mhub,在图中显示为圆环形轮毂。轮毂的内侧和外侧分别是虚拟的可倾瓦油膜轴承和刚度阻尼系统。

图7 转子系统三维有限元模型

分别将xopt和xcon带入有限元模型中,谐响应分析结果如图8所示,分别对应点划线和虚线。优化后相对峰值(10.04-1.65=8.39)同优化前(2.94-1.6=1.34)相比,衰减84.02%。另一方面,目标函数Δn(x)与优化前相比增加了12%,进一步提高了转子系统设计制造的容错能力,同时验证了采用CIMPSO算法得出的优化解的有效性。图中实线为算法中采用传递矩阵法得到的转子不平衡响应。与有限元法相比,最大幅值误差为20.1%,稳态涡动半径和临界转速基本保持一致,这表明采用CIMPSO算法得到的优化解对于转子系统的设计、控制转子的振动具有一定的指导意义。
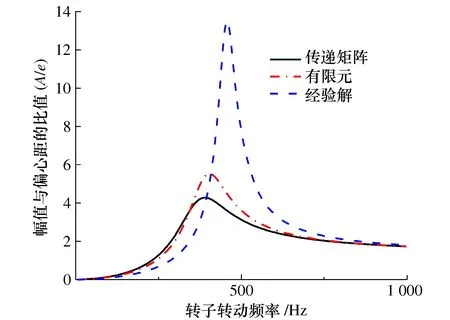
图8 转子系统谐响应分析结果
5 结论
针对超临界二氧化碳微型透平机的转子系统进行了多目标优化设计。基于混沌区间粒子群优化算法,提出了可以考虑设计变量为二维非线性元素的优化设计模型,并归纳总结了混沌区间粒子群优化算法(CIMPSO)。使用该算法对转子系统进行了优化设计,得到了全局非劣最优或者次优解集,验证了算法的稳定性。最后使用商业软件建立有限元模型进行仿真验证,结果表明,经过CIMPSO算法优化后的参数可以显著改善转子的动力学性能。
