在活动中探索分数的意义

2022-07-17韦鑫

快乐学习报·教师周刊 2022年35期

韦鑫

摘要：笔者根据苏教版教材中的分数的意义，在课堂中采用分一分、折一折、比一比的等活动，让学生在活动中积累动手操作经验、合作交流的经验，以及数学思维的运用经验。这些活动经验对于学生将来的数学学习具有重要作用，促进学生数学素养的形成。

关键词：数学思维合作交流数学素养

本课内容是苏教版义务教育课程标准实验教科书三年级上册内容。在此之前，学生已掌握了万以内整数知识的基础。从整数到分数是数的概念的一次扩展，又是学生认识数的概念的一次质的飞跃。无论是意义，还是读写方法、计算方法，分数和整数都有很大的差异。

如何用好教材，帮助学生实现从认识整数发展到认识分数的飞跃？如何在教学过程中，通过适当的教学手段，帮助学生初步感知“几分之一”的内涵，从而提升思维水平？如何通过建立数学与生活以及数学与其他学科的关联，打造有思想有意义有趣味的数学课堂？下面是围绕这些问题进行的教学实践与思考。

一、分一分——感受分数产生的基础

教学侧重引导学生对情景图中的食物进行公平合理的分配。为了引导学生的思维，教学时首先从分苹果和矿泉水入手，引导学生要进行平均分。在此基础上，要求学生对1个蛋糕进行平均分，并对其中的一份进行描述。使他们在活动中认识到：“半个”是生活中的用语，而自己已有的知识经验——整数，不足以用来描述半个蛋糕。这样，不仅激发了学生的学习动机，使其产生学习新的数字的需求，并且，在分一分的活动中，无形中渗透了分数产生的基础——平均分。

出示场景图。

师：小朋友们，你们喜欢和朋友们出去玩吗？小明和小丽这一对好朋友相约来到郊外进行野餐活动，让我们一起来看看，他们都准备了那些好吃的食品？

生：4个苹果、2瓶矿泉和1个蛋糕。

师：你准备怎样帮他们公平合理地分一分呢？

生：平均分，把4个苹果平均分成2份，每份是2个;把2瓶矿泉水平均分成2份，每份是1瓶;最后把1个蛋糕平均分成2份。

师：把一个蛋糕平均分成2份，每份是多少？

生：半个

师：生活中我们用半个表示，那么用数学语言应该怎样表达呢？我们应该用分数来表示，今天我们一起来“认识几分之一”（板书课题）

二、折一折——体会几分之一的内涵

“折一折”的活动侧重引导学生感悟几分之一的内涵，初步理解把一个物体平均分成几份，其中的一份就表示它的几分之一。教学中，一方面鼓励学生利用正方形纸片动手做出分数1/2;另一方面则注重借助成果的展示，帮助他们理解1/2的内涵：不论哪一种分法，只要将这个正方形纸片平均分成2份，每份就是它的1/2。并以此为基础，借助练习题，对学生进行启发：如果把那一个物体平均分分成了3份、4份、5份……又应该怎样用分数来表示呢？有助于学生明确几分之一的内涵——把一个物体平均分成几份，其中的一份就表示它的几分之一。

师：拿出课前准备的正方形纸片，你能表示出它的1/2吗？首先，折一折，画出折痕，然后把它的 1/2 打上斜线。其次，小组交流：你们的表示方法一样吗？完成后坐端正，准备展示。

生：按要求进行小组活动，准备展示交流。

师：请你们小组来到讲台进行展示。

生1：利用磁铁扣将完成的作品（如下图）展示在黑板上，将正方形纸片上下对折，平均分成两份，涂上其中的一份，涂色部分表示它的1/2。

师：哪个小组还有不同想法？

生2：我们小组是这样做的（如下图），将正方形纸片的两个对角重叠进行对折，平均分成两份，涂上其中的一份，涂色部分表示它的1/2。

师：大家同意吗？哪个小组还愿意来展示一下？

生3：我们小组还有不同想法，将正方形纸片左右对折（如下图），平均分成两份，涂上其中的一份，涂色部分表示它的1/2。

师：这三张纸折法不相同，涂色部分形状也不相同，为什么都可以表示它的1/2呢？

生：因为它们都将这个正方形平均分成了2份，每份都是它的1/2。

师：你们真是厉害！刚才，我们一起把一个物体平均分成了2份，其中的一份就是它的1/2，请大家想一想，如果把那一个物体平均分成了3份、4份、5份……又应该怎样用分数来表示呢？（课件出示“想想做做”第一题的四幅图。）

你能用分数表示涂色部分吗？

生：把一个圆平均分成3份，每份是它的1/3;把一个圆平均分成6份，每份是它的1/6;把一个正方形平均分成9份，每份是它的1/9;把一个长方形平均分成8份，每份是它的1/8;

师：通过刚刚的活动以及题目，你有什么发现？

生：把一个物体平均分成几份，其中的一份就表示它的几分之一。

三、比一比——掌握几分之一的大小比较

“比一比”的活动侧重引导学生从利用图形直观比较几分之一的大小，跨越到利用自己思维与推理能力去判断，注重数学的思维层次，从而丰富和加深对几分之一的理解。教学时，先鼓励学生动手操作，再通过涂色面积比较1/2和1/4的大小。在学生初步感知比较大小的方法后，进行与1/8的大小比较，鼓励他们之间合作交流，并体会利用思维进行推理判断。经历这样的活动过程，有助于学生丰富和加深几分之一比较大小方法的理解，提高数学思维水平。

师：小猴子和小猪在一次吃西瓜的时候，也想用我们今天学习的分数，它们都想吃的多。小猴子想：“我要吃这个西瓜的1/2 ”。小猪想：“我肚皮大，吃的多，要吃这个西瓜的1/4”它们谁吃得多？为什么？

学生意见不一，一部分认为小猴吃得多，剩下的认为小猪吃的多。

师：数学可是一门严谨的学科！我们来借助图形验证猜测。请拿出事先准备的圆片，女生利用它做出1/2，男生利用圆片做出1/4。

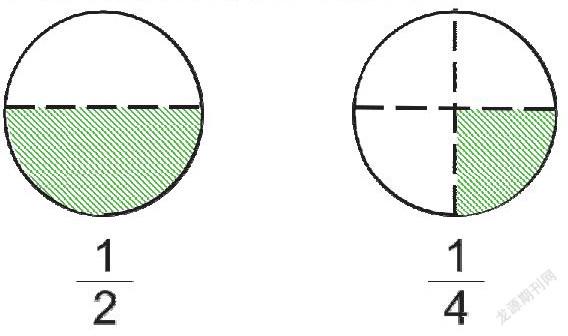
分女生组、男生组进行展示（如下图）

通过图片直观比较发现：1/2 > 1/4

师：课件出示动画，大象也来了，它说：“我的饭量最大，要吃西瓜的1/8”大象吃的是最多的吗？

生：不是。

师：同桌互相一下交流想法。

生1：利用圆片，将它对折3次，平均分成8份，涂上其中的1份，和刚刚的1/2、1/4涂色部分相比，1/8涂色面积最小，所以大象是吃的最少的。

师：你的动手能力真厉害！这个方法很直观！谁还有不同想法？

生2：我没有动手折纸片。我是这样想的，1/8表示把这个西瓜平均分成8份，吃其中的1份，同样一个西瓜，平均分的份数越多，其中的1份就越小。

师：所以说，同样一个物体，平均分的份数越多，每一份就越小。那我们应该怎样比较几分之一的大小呢？