含槽变截面悬臂式压电俘能器性能研究

蔡 浩，周星德

(河海大学 土木与交通学院，江苏 南京 210098)

0 引言

微机电系统可以直接从工作环境中获得能量，这对于存在环境激励而又更换电池难的场合具有重要意义，已经成为研究的热点之一[1]。压电俘能器有两端固定式、一固一铰式、悬臂式，可以适用于不同场合，其中，悬臂式压电俘能器研究较多，文献[2]提出增加压电陶瓷铺设数目来增大悬臂梁固有频率，减小自由端最大位移，同时保持各监测点应变值不变。增大俘获能量的方法主要有以下两种：

1)采用并联的方式[3]。虽然该方式结构复杂，但在增加能量的同时，可以加宽带宽。

2)采用变截面形式。近期有关此方面的研究较多，梁形式可以采用等厚度梯形[4-5]、等厚度矩形+三角形[6]、变厚度圆台[7]等，结构稍微复杂，但俘获能量有明显提高。为了进一步提高俘获的能量，在采用变截面形式的前提下，近期出现了在梁基体上挖槽来提高俘获能量的方式[8-9]，可以是等厚度单槽、等厚度多槽、变厚度单槽等，通过仿真可看出俘获的能量得到提高。

目前有关梁基体挖槽的研究，梁形式还是采用矩形+三角形的模式，为了进一步提高俘获的能量，本文提出了按指数变化的梁形式，以期获得更大的俘获能量，具体过程如下：

1)梁形式采用指数变化，并且内部挖槽。

2)推导对应的振动方程，确定振型表达式，进而写出特征方程。

3)推导电压和输出功率表达式，并根据电压和输出功率确定最优指数。

最后，本文给出一个仿真实例说明了该方法的有效性。

1 悬臂式压电俘能器模型

1.1 模型详图

图1为悬臂式压电俘能器结构图(n>1)，图中L为结构截断前的总长度,L1=L/3为结构截断后自由端与截断前自由端的距离，L2=2L/3为结构截断前压电片与自由端的距离，h为梁的总高度，bm为压电片的宽度，br为梁固定端的宽度。结构在x=L1处截断并安装电磁激励器。

图2为压电俘能器第二部分详图，梁的总高度h=h1+h2+h3+hp，其中h2，hp分别为矩形槽和压电片的厚度，h1、h3分别为矩形槽与梁上下端之间的距离。中性轴与压电层中点的距离为yc。

1.2 运动方程

利用欧拉伯努利梁理论建立模型[10]为

f(x,t)

(1)

其中：

M(x,t)=E(x)I(x)∂2y(x,t)/∂x2

(2)

m(x)=ρA(x)

(3)

式中：M(x,t)，c(x)，m(x)，E(x)，I(x)分别为弯矩、阻尼系数、单位长度质量、刚度和惯性矩；ρ为密度；y(x,t)为横向位移；A(x)为横截面积；f(x,t)为外激振力。

对于等厚度锥形梁，宽度b(x)=bL(x/L)n，其中bL为锥形梁固定端的宽度，锥形梁的弯曲程度由系数n决定，任意位置的横截面积和任意位置的惯性矩为

A(x)=AL(x/L)n(0≤x≤L)

(4)

I(x)=IL(x/L)n(0≤x≤L)

(5)

AL=bLh(0≤x≤L)

(6)

(7)

无阻尼自由振动为

(8)

令梁的位移为y(x,t)=W(x)eiωt，其中ω为结构的自振频率，代入式(8)可得：

(9)

将式(4)、(5)代入式(9)可得：

(10)

将式(6)微分可得：

(11)

图1中第一部分和第二部分的振型可表示为

(12)

(13)

λ4=16ρALω2L2/(EIL)

(14)

式中：AL，IL分别为x=L时的截面面积和惯性矩；Jn,Yn分别为第一、二类的n阶贝塞尔函数；In,Kn分别为第一、二类的n阶修正贝塞尔函数；C1,C2,C3,C4,C5,C6,C7,C8为待定常数。

图2中第二部分结构的中性轴Na(x)和每层的惯性矩Ij(x)分别为

(15)

(L2≤x≤L)

(16)

式中Ej,hj分别为第j层的杨氏模量和厚度，j与i取值分别为1，2，3，4和2，3，4。

将压电层中点作为y0，y0到Na(x)的距离为

(L2≤x≤L)

(17)

1.3 边界条件及连续性条件

1)当x=L1时,有：

(18)

(19)

2)当x=L时，有：

W2(L)=0

(20)

dW2(L)/dx=0

(21)

连续性条件为

当x=L2时,有：

W1(L2)=W2(L2)

图6为数值模拟得到的激光打孔中熔融物的喷溅过程图，激光能量为21J。图中深色与浅色部分分别表示气体和铝板，相交处是两种物质的过渡。由图6(a)可知在打孔刚开始阶段，熔融物喷溅行为还比较弱，此时孔内的气压还比较小，且孔深还比较浅，孔壁比较平缓，熔融物的喷溅方向基本是垂直于材料表面的。在0.3～0.4 ms(图6(b)、图6(c))时，熔融物的喷溅行为比较剧烈，继续到0.5 ms时(图6(d))孔深进一步增加，可看到熔融物的喷溅开始减缓，这是由于孔形成后，底面变成了曲面，不利于熔融层内形成这种压力，再者孔壁的坡度逐渐增加，也增加了熔融物喷溅的难度。

(22)

(23)

(24)

(25)

1.4 受迫振动的解及输出电压

特征方程为

η8×8C8×1=0

(26)

式中：η为特征方程；C为模态系数向量，其表达式为

C=[C1,C2,C3,C4,C5,C6,C7,C8]T

(27)

令系数阵行列式为0可求系统特征值，即:

|η8×8|=0

(28)

在梁的端部施加荷载Psin(ω′t)(其中ω′为外激频率)，则有：

y1,2(x,t)=W1,2(x)GL-1pW2(L)sin(ω′t)/α

(29)

其中：

(30)

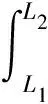
(31)

式中ζ为阻尼比。

电磁激励器通电后，线圈在梁端产生的力p[9]为

(32)

式中：Nc为线圈的转数；I为通电线圈电流大小；A为横截面积；D为永磁体的半径。

由压电片产生的输出电压为

(33)

(34)

(35)

(36)

式中Cp为电容。

2 仿真分析

利用第一节给出的模型，通过仿真对图1、2所示的压电俘能器的性能进行评估，梁和压电贴片的尺寸如表1所示。

通过改变电磁激励器的输入值，使施加的外激力恒定为0.1 N,Cp=65 nF，压电俘能器的ζ=0.002 2。图3为使用MATLAB给出了当锥形梁的弯曲程度系数n=1.8、1.6、0.8时，输出电压与外激频率间的关系。

由图3可知，将n=0.8～1.8时可得到不同n值对应的输出电压，将n与输出电压进行回归分析，得到的结果如图4所示。

3 结束语

对于悬臂式压电俘能器，文献[8-10]已经验证了挖槽能够提高输出电压，其梁形式采用矩形+三角形的简单模式。为了进一步提高俘获的能量，本文提出了按指数变化的梁形式，以期获得更大的俘获能量。通过仿真发现,在保持梁长度不变的前提下，指数越大，则输出电压及功率越大，但系统的特征频率也变大，因此，在实际应用中应根据实际需要确定合适的指数。