基于超材料结构的悬臂梁水听器设计
2022-07-16常文娟赵永成廖力鸣郝程鹏
常文娟,赵永成,廖力鸣,闫 晟,郝程鹏
(1.中国科学院声学研究所,北京 100190;2.北京新兴东方航空装备股份有限公司,北京 100195)
0 引言
当前海洋工程领域包括海底地形地貌探测、海底资源勘探及海洋环境监测等,并且现代舰船的辐射噪声集中在十几赫兹到几百赫兹的低频段,所以开展低频水听器的研究需求迫切[1-2]。
传统水听器的工作频带可覆盖几赫兹到几十千赫兹,属非谐振频段[3-5]。如果水听器在低频段以谐振方式接收水声信号,其灵敏度可得到大幅提升[6],但这会导致水听器尺寸显著增加、工作频带变窄等问题。传统水听器设计方法无法同时解决上述难题,一个可行的解决途径是在水听器的结构设计中引入超材料功能结构设计理念,利用超材料结构的负质量、负密度、负弹性模量等特性[7-9],通过低频局域共振来降低水听器的谐振频率[10-11]。
超材料结构是一种人工周期结构,可以根据实际需求进行设计,具有很高的设计自由度。大量的理论和实验研究表明,超材料结构具有丰富的声学特性,不但能充实振动与声学方面的理论研究,更有望在声学领域开辟一门新的技术学科,形成颠覆性的技术革新[12-13]。超材料结构目前已在低频减振降噪、声成像、人工耳蜗、水下通信及探测等空气声学和水声学功能器件的设计方面实现应用,其低频宽带特性还可用于多种水下水听器及传感器的设计[14]。在水声功能器件方面,超材料结构的研究主要集中在水下吸隔声、声开关、水下声隐身、水声聚焦透镜、声投射仪等方面[15-19],而应用超材料结构的水听器鲜有报道,故将超材料结构与水听器设计相结合具有一定的开创性。
面向当前低频水听器的发展需求,本文基于超材料结构设计出一种新的悬臂梁水听器[20],在不增大体积尺寸的条件下,有效降低了水听器的谐振频率,并获得较高的低频接收灵敏度。所设计的水听器具有结构简单、尺寸小、质量小、灵敏度高等优点,同时具有良好的低频性能和温度稳定性。将该水听器安装于刚性球壳中可制成矢量水听器,其具有探测距离远、灵敏度高、可靠性高等优势。
1 声学超材料负等效特性原理
将超材料结构引入低频水听器设计可以降低水听器的谐振频率,满足水听器的低频发展需求。本文基于固体力学中对于悬臂梁各阶模态的研究,使用超材料结构降低水听器的谐振频率。主要考虑一阶共振情况,这是因为一阶共振频率低且变形大,对于水听器灵敏度的提升作用显著。针对如何降低振动悬臂梁的谐振频率,传统手段是采用加长悬臂梁长度或增加悬臂梁头部质量,而利用声学超材料结构可在不改变悬臂梁尺寸情况下降低谐振频率,能够更好地解决这一问题。
通常情况下,降低系统结构的刚度可以使谐振频率降低,但对于本文设计的结构而言,常用降低刚度的方法,如开方形槽或圆孔会削弱结构的整体稳定性,不能满足工程的实际应用。因此,本文采用声学超材料设计了一种局域共振梁结构来降低谐振频率,该结构是由金属、橡胶、金属组成的一种周期结构,如图1所示。
由图1(a)、(b)可知,结构的刚度下降,但整体的稳定性却并未改变。图1(c)是图1(b)模型的等效图,其中橡胶等效为弹簧k,并由k连接局域共振质量m2和基座质量m1。在分析过程中,首先假设其为理想模型,即不考虑橡胶弹簧的质量等问题,再在纵轴方向对质量块m1和m2分别进行平衡条件分析。根据牛顿第二定律,系统的运动方程如下:
(1)
(2)
x1(t)=X1exp(iωt)
(3)
x2(t)=X2exp(iωt)
(4)
式中:Fn为系统所受的外力;ω=2πf为角频率,f为系统振动频率;X1、X2分别为位移x1(t),位移x2(t)的幅值。联合式(1)~(4),得到该结构的等效质量公式为
(5)
为了能直观地看出系统等效质量和振动趋势的情况,对上述公式中的参数进行取值:k=1 N/m,m1=1 kg,m2=1 kg,Fn=1 N。经计算可得系统的动态等效质量和动态响应函数曲线,如图2所示。
由图2可知,所设计的模型具有负等效质量特性。进一步分析该图可知,当激励频率在低频范围内,此时的等效质量meff=m1+m2。该结果表明低频时,在激励作用下的基体质量块和谐振质量块具有相同的振动方向;频率逐渐增加,当频率到达系统的共振频率附近时,此时的等效质量发生突变,整个曲线呈现指数型增加,此时的等效质量meff远大于m1+m2。因此,在共振频率附近,系统质量无限大,此时系统对于激励不做出任何反应。由图2可知,在共振频率处,位移的响应为0。在共振频率前后,等效质量由正变负,由此可知此时的谐振质量块和基体质量块的运动方向相反,且谐振质量块起主要作用,从而使整个系统与激励方向相反。经过共振频率后,随着激励频率的进一步增大,等效质量由负变成正,这时等效质量变化并非突变,存在等效质量为0的点。
2 超材料结构悬臂梁局域共振结构设计
利用声学超材料的负等效原理,设计周期结构的悬臂梁。考虑到实际工程应用,薄板材料选择为铜,弹簧材料使用橡胶,悬臂梁尺寸(长×宽×高)为20 mm×20 mm×1 mm,其余参数如表1所示。
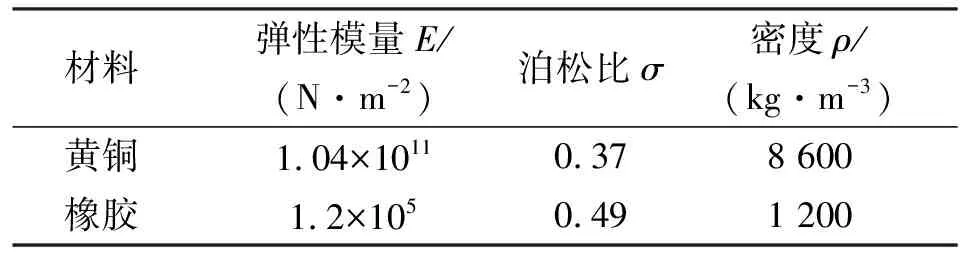
表1 材料参数
2.1 悬臂梁分层数对一阶固有频率的影响
悬臂梁系统由一阶共振振动带动压电材料进行工作,其一阶固有频率非常重要。为此计算了单纯铜梁、三层铜-橡胶梁、五层铜-橡胶梁的一阶固有频率,结果如表2所示。由表可知,当中间加上一层橡胶时,一阶固有频率约下降至651 Hz。随着层数的增加,特征频率不断下降,但下降幅度在减少。虽然层数越多,一阶固有频率越低,但考虑到加工难度,层数不宜过多,故而选择了三层的铜-橡胶-铜结构。

表2 一阶固有频率随层数变化
2.2 橡胶的密度对一阶固有频率的影响
在上述工作的基础上对层数进行优化,需要在三层结构的基础上考虑橡胶的密度问题。为此,将表1中的橡胶密度改为500 kg/m3、1 000 kg/m3和1 500 kg/m3进行分析,得到悬臂梁的一阶固有频率,如表3所示。结果表明,随着橡胶密度的增加,悬臂梁的一阶固有频率逐渐降低;但随着密度的变化,频率的变化幅度较小,这说明橡胶的密度对于一阶固有频率的改变效果小,不是影响其性能的主要因素。表3为一阶固有频率随橡胶密度变化表。
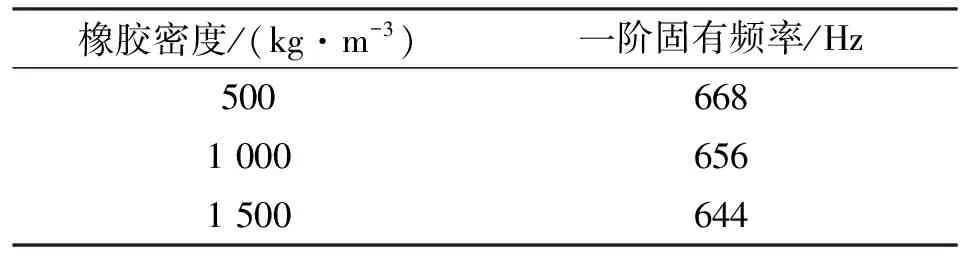
表3 一阶固有频率随橡胶密度变化
2.3 橡胶弹性模量对一阶固有频率的影响
对材料的弹性模量参数进行分析,考虑设计橡胶的弹性模量分别为1×105N/m2、1×106N/m2、1×107N/m2、3.5×107N/m2,共4个样本,计算其一阶固有频率,结果如表4所示。结果表明,随着弹性模量的增加,一阶固有频率不断上升。在低弹性模量阶段,一阶固有频率变化不大,但在高弹性模量范围内,一阶固有频率变化较大。

表4 一阶固有频率随橡胶弹性模量变化
2.4 铜片厚度对一阶固有频率的影响
基于上述分析,在三层结构的基础上继续考虑铜片厚度的问题,设计了3种不同厚度(0.25 mm、0.2 mm、0.15 mm)的样本,计算其一阶固有频率,结果如表5所示。由表可见,结构中的铜片越薄越好。

表5 一阶固有频率随铜片厚度变化
综上所述,对于充当填充物的橡胶,其密度对悬臂梁的一阶固有频率影响不大,但弹性模量不同,其值越低,悬臂梁的一阶固有频率也越低。由此可知,采用普通橡胶可满足降低一阶固有频率的要求。
3 超材料结构悬臂梁局域共振结构仿真分析
根据上述分析,设计了基于超材料结构的悬臂梁,它由中间复合多层声学超材料、压电晶体组成。为了验证超材料结构悬臂梁的优势,通过仿真对超材料结构悬臂梁与传统结构悬臂梁通过仿真进行对比分析[21-23]。首先仿真分析了传统悬臂梁结构模型,建立其有限元模型,如图3所示。图中金属基座部分作为夹持端,位移为0。悬臂梁采用铜基材,粘接压电单晶片。经仿真计算可知,传统悬臂梁结构的一阶谐振频率为2 214 Hz。在谐振状态下,悬臂梁做上下摆动,其振动位移如图4所示。
进一步分析采用超材料结构的悬臂梁模型,建立其有限元模型,如图5所示。悬臂梁采用铜-橡胶-铜分层结构,金属基座部分作为夹持端,位移为0。超材料结构悬臂梁的一阶谐振频率为1 098 Hz。在谐振状态下,超材料结构悬臂梁做上下摆动,其振动位移如图6所示。
对比图4、6可知,采用超材料结构的悬臂梁作为水听器的功能结构,在相同尺寸的条件下,其谐振频率明显降低,由2 214 Hz降为1 098 Hz。在约1 000 Hz时,利用谐振频段进行信号探测,实现了高灵敏度的远程探测,可应用于浮标、潜标、UUV等平台,还可用于制作矢量水听器。
4 结束语
本文将声学超材料结构引入悬臂梁水听器设计中,利用超材料的负等效质量特性,设计了局域共振悬臂梁结构。通过分析各材料参数对悬臂梁的一阶固有频率的影响,完成了基于超材料结构的悬臂梁水听器设计。仿真分析结果表明,本文设计的悬臂梁水听器的谐振频率为1 098 Hz,可在低频段以谐振方式进行水下信号探测,同时具有高接收灵敏度、工程上易实现等特点,具有较好的应用前景。
