基于Anylogic的兰州西站高架层客流组织优化仿真研究

刘凯　梁辉

摘要：随着电子客票的迅速普及和客运站服务水平的提高，旅客在客运站逗留的时间也日渐缩短，但大型客运站的运输设备配置和流线优化等依然存在可改进的地方。本论述以兰州西站高架层为研究背景，为旅客进站构建购票-安检排队论模型，以Anylogic仿真软件为依托，搭建高架层的仿真模拟环境;最后指出在电子客票的大背景下，限制旅客进站的主要因素是安检设备，并通过调整各设备的数量和位置，使高架层的服务等级达到 A 等级。

关键词：高铁客运站;客流流线优化;排队论;Anylogic;仿真评价

中图分类号：U293.13文献标志码：A

0 引言

国外对客运站旅客流线优化的研究起步较早： Marin Dubroca-Voisin等[1]研究发现公共交通轨道站构成了复杂的系统，其中客流对运营和交通条件有重大影响;Meng Shi 等[2]提出基于网格结构的建筑疏散模拟介观模型并使用商业包Anylogic来基准测试该模型性能;Fang Li 等[3]提出一种行人疏散模型，將社会力模型和数学模型结合起来;Lukas Asmer等[ 4] 建立德国 Brunswick 火车站模拟模型，用于调查额外安全检查对客流的影响;BoweiJin等[5]研究多危害耦合条件下密集地铁站节点破坏下疏散的时空分布特征。

针对客运站旅客流线优化，我国也进行了诸多探索：戴建强[6]应用排队论理论和Anylogic软件仿真，研究了目前既有站和部分高铁站进站排队时间过长和用户体验差的问题;张光远等[7]应用Anylogic仿真模型，根据仿真结果提出不同待检票人数时，各类检票闸机的数量和人员安排;段胜利[8]利用Anylogic软件建立了齐齐哈尔站的仿真模型，找到了限制旅客进站的瓶颈所在并提出优化方案;赵亮[9]运用Anylogic软件仿真了武昌站的客流流线，统计了平均排队长度、等待时间等指标;张晓东[10]建立了基于SIMIO 仿真软件的大庆西站仿真模型。

本论述从旅客的进站流线入手，分析兰州西站旅客的大致来源和特点，对旅客流线组织现状及设备配置进行分析，然后分析旅客进入高架层候车大厅中的走行路线，主要对高架层设备运用和客流组织优化等问题进行研究;核心是基于兰州西站高架层旅客流线进站排队论以及运用Anylogic仿真软件平台对高架层旅客进站进行仿真，通过优化客运设备的配置来解决进站流线问题，提高服务水平;并提出提高旅客进站效率的措施，通过仿真验证其合理性。

1 兰州西站客流流线分析

流线是指在客运站内，旅客、行包、交通车辆的流动过程和流动线路[11] 。流线按流动方向不同可分为进站和出站两大流线。

目前兰州西站旅客进站过程如图1 所示。

旅客在进站区的总时间包括旅客的平均走行时间、接受服务时间以及排队等待服务时间。具体的服务等级标准见表1 所列[14] 。

2 基于排队论的兰州西客站流线模型

高峰期的进站客流服从泊松分布，人工售票（或自助售票机售票）的服务时间服从负指数分布，安检环节的服务时间服从定长分布。从客运站的角度，排队长Lq主要是车站工作人员关心的问题;从旅客的角度，等待时间Wq主要是旅客关心的问题。基于此，本论述旨在建立二阶排队论模型，第一阶段为人工售票（或自助售票机售票），第二阶段为安检环节。

旅客进站流线主要分为以下三类：

流线一：旅客进入高架层→人工服务窗口购票→实名制验票→安检→旅客进入候车大厅候车;

流线二：旅客进入高架层→自助售票机购票（取票）→实名制验票→安检→旅客进入候车大厅候车;

流线三：旅客进入高架层→安检→旅客进入候车大厅候车。

2.1 变量给定和基本假设

（1） 所有进站旅客间隔时间均服从参数为λ的泊松分布且相互独立，分别以 a1、a2、a3的概率表示流线一、流线二、流线三的旅客比例;

（2） 设人工售票窗口数为c1，服务时间服从参数为μ 1 的负指数分布，自动售票机数为 c2，服务时间服从参数为μ2的负指数分布，安检机器数为 c3，服务时间服从参数为 D 的定长分布;

（3）服务系统采用先到先服务的原则，且其容量无限大;理论上认为旅客在结束第一阶段服务后会全部进入第二服务阶段，因此转换率为1;

（4） 假设排队论系统的服务强度ρ11 。

2.2 模型构建

流线1 由人工售票和安检两级构成。人工售票视为 M/M/C 排队论系统，同理，流线2 由自动售票机和安检两级构成，自动售票机视为 M/M/C 排队论系统。

流线1、流线2、流线3 都要经过安检环节，因此第二级服务系统安检被视为 M/D/C 排队论系统。

2.3 模型应用

本论述主要研究对象是从兰州西站高架层进站的旅客流线。拟定了4 个比较方案，具体的客运设备配置数量见表2 所列。

进站流线旅客到达服从泊松分布，人工售票和自助取票机服从负指数分布，安检服务器服从定长分布，具体参数取值见表3 所列。

利用 MATLAB 软件对以上排队论模型进行求解，得到逗留时间Ws和等待时间Wq这两个重要指标（单位：min），具体结果见表4～ 5所列。

对于表中的数据做如下分析：

（1） 方案一：在兰州西站高架层现有设备的条件下，旅客平均进站时间为20 min 左右，进站时间较长;

（2） 方案二：在其他设备不变的条件下，增加3 个人工售票窗口，旅客平均进站时间为15 min 左右，比目前进站时间降低了7.87%;

（3）方案三：在其他设备不变的条件下，增加4 台自助机，旅客平均进站时间为16 min 左右，比目前进站时间降低了6.08%;

（4） 方案四：在其他设备不变的条件下，增加2 个安检设备，旅客平均进站时间为10 min 左右，比目前进站时间降低了32.78%，旅客进站时间大大缩短。

3 基于Anylogic的高架层进站客流仿真模型

3.1 仿真内容介绍

（1）仿真一：对高架层现有正常运营设备进行仿真，分析各个设备的繁忙程度以及排队长、等待时间等因素;

（2） 仿真二：调整人工售票窗口、自助售票机以及安检设备的数量，通过调整各个设备的数量，从而找到影响旅客进站时间的主要限制因素，具体调整方案见表 6所列;

（3）仿真三：开放高架层所有预留设备，模拟高架层最大服务能力，并检验其效果;

（4） 仿真四：模拟当高架层发生火灾等事故的条件下，高架层旅客从高架层进站口撤出的过程，并分析其撤出时间。

3.2 仿真结果分析

如图2 （1） 、（2） 、（3）、（4）所示，为高架层不同角度的仿真图像。

3.2.1仿真一的结果

运行模型，高架层旅客进站时间比例如图3 所示（单位：s），时间大致分布在250～ 1000 s 之间，最大值为1 437 s，最小值为65 s，均值为566 s，偏差为270 s。各设备总队长及其比例如图4 所示（单位：m），人工售票窗口和自助售票机前基本无拥堵排队情况，由此猜想整个高架层的大量排队现象主要集中在安检设备环节。

3.2.2仿真二的结果

运行模型，结果见表7 所列。

由此可知，三个设备对高架层进站时间分布影响：安检设备>自助售票机>人工售票窗口。安检设备的数量是整个高架层进站时间的瓶颈，验证了仿真一的猜想。3.2.3仿真三的结果

运行模型，高架层旅客进站时间比例如图5 所示（单位：s），时间大致分布在70～ 150 s 之间，最大值为378 s，最小值为59 s，均值为133 s，偏差为60 s 。各设备总队长及其比例如图6 所示（单位：s）。

3.2.4仿真四的结果

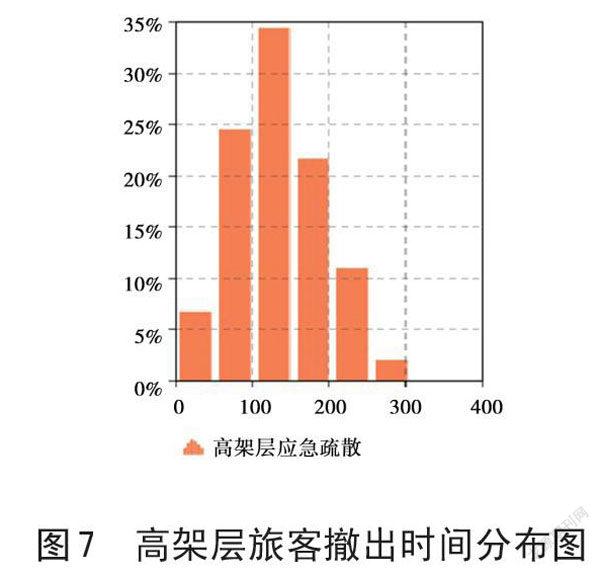
运行模型，高架层旅客撤出时间比例如图7 所示（单位：s），时间大致分布在100～ 150 s 之间，最大值为304 s，最小值为3 s，均值为137 s，偏差为58 s。

3.3 旅客流线优化措施

（1） 通过调整自助售票机的位置和数量，减少旅客走行距离，避免流线交叉，提升高架层的服务效率。

（2） 适当减少自助售票机和人工售票窗口的数量，增大高架层的空余空间，为旅客提供舒适的视觉感官服务，同时，增加安检设备数量和人员，通过改善安检这一瓶颈来提升高架层的服务效率。

（3）在安检环节，为了更高效率的提高服务水平，可以将旅客进行分流。

具体设备位置和数量调整如图8 所示。

3.4 优化后结果输出

高架层旅客进站时间比例如图9 所示（单位：s），时间大致分布在80～ 220 s 之间，最大值为404 s，最小值为 60 s，均值为132 s，偏差为59 s 。各设备总队长及其比例如图10所示（单位：m），人工售票窗口和自助售票机前基本无拥堵排队情况，安检设备环节存在少量排队情况。这样高架层的平均服务水平为 A 等级，最差也为 C 等级。

4 结论

本论述首先分析了兰州西站进站旅客的走形路线，依托排队论模型对旅客进站过程构建了理论基础。分别建立了 M/M/C 购票模型和 M/D/C 安检模型，通过4 个方案对旅客进站时间进行对比，找到了限制旅客进站的主要因素为安检设备。其次，依托Anylogic仿真平台对旅客进站过程构建了仿真模拟。利用行人库社会力模型对高架层进站区进行仿真。分别模拟了：（1） 在大客流（春运，节假日等）的条件下，兰州西站高架层在现有设备和完全开放预留设备的条件下高架层的服务质量;（2）在发生意外（火灾，恐怖袭击等）的条件下，高架层旅客应急疏散所需要的时间。最后，本論述指出安检设备是旅客进站的瓶颈，并结合电子客票的普及，提出了优化高架层旅客流线的具体措施，并做出仿真验证结果，结果表明高架层经流线优化后，服务等级可达到 A 等级。

参考文献：

[1] MarinDubroca- Voisin，BacharKabalan，Fabien Leurent.On pedestrian traffic management in railway stations：simula⁃ tion needs and model assessment[J].Transportation Research Procedia，2019（37）：3-10.

[2] Meng Shi，Eric Wai Ming Lee，Yi Ma. A Newly developedMesoscopic Model on Simulating Pedestrian Flow[J].Proce⁃ dia Engineering，2018，211：614-620.

[3] Fang Li，Shaokuan Chen，Xiudan Wang，et al. Pedestrian Evac⁃uation Modeling and Simulation on Metro Platforms Consider⁃ ing Panic Impacts[J].Procedia - Social and Behavioral Scienc ⁃ es，2014，138（14）：314-322.

[4] Lukas Asrmer， Andrei Popa， Tobias Koch， et al. Secure rail sta⁃tion - Research on the effect of security checks on passenger flow[J].Journal of Rail Transport Planning & Management，2019（10）：9-22.

[5]BoweiJin，Jinghong Wang，Yan Wang，et al. Temporal andspatial distribution of pedestrians in subway evacuation under nodefailurebymulti- hazards [J].SafetyScience，2020（127）：104695.

[6]戴建强. 基于排队论和Anylogic仿真的车站进站排队优化[J]. 铁路计算机应用，2018（9）：40-43.

[7]张光远，胡悦，胡晋，等. 基于AnyLogic仿真的无纸质检票时间研究[J].铁道运输与经济，2020，42（2）：35-41.

[8]段胜利.齐齐哈尔站客运设施配置及流线优化研究[D].大连：大连交通大学，2017.

[9]赵亮.武昌客运站乘客流线优化仿真研究[J].铁路通信信号工程技术，2019（10）：25-29，66.

[10]张晓东.大庆西站客流组织与客运设施配置仿真分析[D].大连：大连交通大学，2015.

[11]王甦男，贾俊芳. 旅客运输[M]. 北京：中国铁道出版社，2008.

[12]宫宇姝.大型铁路客运站进站流线优化与仿真研究[D].兰州：兰州交通大学，2018.