不完全信息和模糊厌恶下DC型养老金最优投资策略

王 佩, 李仲飞, 张 玲

(1.广东金融学院 经济与贸易学院,广东 广州 510521; 2.南方科技大学 商学院金融系,广东 深圳 518055)

0 引言

寿命延长和出生率下降导致大多数国家养老金制度可持续性经受严峻挑战，养老基金投资与风险管理重要性日益凸显。作为养老金模式的主要类型之一，确定缴费型(Defined contribution，DC)养老金的缴费是预先确定的，DC型养老金参与者(以下简称参与者)退休时能够领取到的金额依赖于累积期内养老金账户的投资收益。此时，养老金发起人承担的长寿风险和财务风险等转移给了参与者。从这个角度看，DC型养老金的投资对于维持养老金支付制度的持续性具有重要意义。近二十年来，许多学者以最大化退休时养老金账户财富的预期效用为目标，研究DC型养老金的最优投资决策问题。由于养老金的投资通常会持续20至40年，在如此长期的投资期限中利率随机波动和工资随机变化的风险对DC型养老金账户的最终财富水平有显著影响。因此，Boulier等[1]和杨嶙等[2]利用Vasicek利率模型研究了随机利率对DC型养老金最优投资策略的影响。

在上述DC型养老金最优投资策略的研究中，刻画风险资产价格的随机微分方程中的漂移参数通常设置为常数或时间的确定性函数，这意味着股票等风险资产的瞬时收益率可被决策者准确地获得。然而，投资实践中，决策者只能从金融市场获得有限的信息，例如股票的历史价格，而不是股票当前的瞬时收益率。通常，决策者尽可能多地收集金融市场信息来估计股票预期收益率，并基于股票预期收益率的估计做出投资决策。这就导致了不完全信息下DC型养老金最优投资问题。同时，实证和理论研究也证实股票预期收益的可预测性，因此投资者可利用一些经济变量来预测股票的预期收益，如近期的股票收益、市盈率和账面市值比等，详见Fama和French[3]。这些研究成果也被引入DC型养老金投资问题的研究中，如Li等[4]在均值-方差准则下研究了不完全信息和股票收益可预测性下DC型养老金的均衡投资策略，Zhang等[5]在离散时间框架下研究了金融市场信息部分可观测对DC型养老金多阶段最优投资策略的影响。他们的研究表明，不完全信息和股票收益可预测性的引入导致DC型养老金的均衡投资策略和最优投资策略不再是短视的，而是依赖于剩余投资期限。因此，临近退休时刻股票的最优投资比例会逐渐降低，这与DC型养老金的投资实践是一致的。故在DC型养老金最优投资问题中考虑不完全信息和股票收益可预测性符合DC型养老金投资的实际特征。

相较于金融市场信息完全可观测的设定，不完全信息和股票收益可预测性的引入使得DC型养老金投资决策模型的参数不再是确定的，但这仅是决策者面临的不确定性之一。这里有一个隐含的基本假设，即决策者确切地知道控制当前金融市场动态演变的真实概率测度，这个真实概率测度不仅控制着决策模型的准确性，还决定着模型参数估计的准确性。然而，即使是具有强大信息搜集能力的机构投资者，也不可能对金融市场的真实概率测度有精准的掌握，这种由于缺乏有关概率测度信息而引起的不确定性被称为模型模糊性(或模型不确定性)。通常来说，决策者是厌恶模型模糊性的(Bossaerts等[6])。 虽然在制定投资决策时，决策者会设定一个概率测度，但决策者怀疑这个特定概率测度并不是控制金融市场运行的真实概率测度。因此，决策者仅将这一特定的概率测度作为参考测度，进而去寻找一组与参考测度等价的替代概率测度，通过“同质鲁棒性控制方法”可以得到决策者模糊厌恶下的动态投资组合策略(Anderson等[7]、Maenhout[8])。近年来，Wang和Li[9]、Wang等[10]和Zeng等[11]研究了模糊厌恶下具有不同背景风险的DC型养老金最优投资问题。他们的研究表明模糊厌恶导致DC型养老金最优投资策略更为保守，且忽视模型模糊性会使DC型养老金决策者遭受巨大损失。然而，这些研究只着重分析模糊厌恶和背景风险的影响，将金融市场信息仍然设定为完全可观测。

现有研究或单独分析不完全信息对DC型养老金投资策略的影响，或从决策者的角度分析模糊厌恶对DC型养老金最优投资策略的影响，未发现有文献综合分析不完全信息和模糊厌恶对DC型养老金最优投资策略的影响，这正是本文的立意之一。在信息部分可观测的金融市场中，本文考虑股票收益可预测性和模糊厌恶同时作用下DC型养老金最优投资问题，从参与者的角度构建优化决策模型。由于DC型养老金的投资期限通常较长，因此假设利率是随机的更为合理，并使用Vasicek模型来刻画利率的动态演化过程。另外，参与者的工资被假设为随机的，并遵循几何布朗运动。假设参与者是模糊厌恶的，且他只能观测到有关股票价格和利率的信息，无法观测到有关预测因子的信息。基于以上设置，本文构建了不完全信息和模糊厌恶下股票收益具有可预测性时DC型养老金最优投资模型，利用滤波技术和动态规划原理，得到了最优投资策略和相应值函数的解析解。

本文的主要贡献在于：(1)在DC型养老金最优投资问题中，同时考虑股票收益可预测性、 不完全信息和模糊厌恶；(2)分别分析了不完全信息和模糊厌恶对DC型养老金最优投资策略的影响；(3)对同时考虑不完全信息和模糊厌恶时的最优投资策略、仅考虑不完全信息时的最优投资策略和仅考虑模糊厌恶时的最优投资策略进行了比较静态分析。

本文的组织如下：第1节为模型构建；第2节通过模型求解得到最优投资策略；第3节对最优投资策略进行敏感性分析；第4节总结本文；附录给出了本文主要推导过程。

1 模型构建与求解

设(Ω,F,{Ft}t∈[0,T],P)为一个完备概率空间，其中Ft表示到时刻t为止金融市场中的信息，[0,T]为固定有限的投资期限。假设本文中所有的随机过程均是此赋流概率空间上的适应过程。为简单起见，假设投资交易活动持续进行，且不存在交易成本和税费。

1.1 金融市场和工资

在金融市场上，参与者可将其养老金账户中的财富投资到一个无风险资产(如银行账户、现金)、一个股票和一个滚动债券。无风险资产的价格过程S0(t)满足如下常微分方程：

(1)

其中r(t)是瞬时利率。由于DC型养老金的投资期限通常为20～40年，因此瞬时利率r(t)不可避免地随金融市场的波动而变化。为体现瞬时利率的随机特征，用Vasicek模型刻画的动态演化过程：

dr(t)=a(b-r(t))dt-σrdWr(t)

(2)

其中a>0是r(t)的均值回复速率，b>0是长期平均瞬时利率水平，σr>0是r(t)的波动率，Wr(t)是关于Ft的一维标准布朗运动。

根据金融市场理论，利率的上升和下降显然会影响金融市场的表现，特别是许多金融资产(如股票)的价格。因此，本文中股票价格过程S(t)由如下几何布朗运动刻画:

σS2(μ(t)dt+dWS(t))

(3)

(4)

金融市场上的第三种资产是滚动债券。到期日为固定值K的滚动债券在时刻t的价格BK(t)满足

(5)

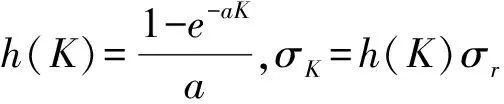
参与者在退休时刻T前连续不断地向其养老金账户缴纳固定比例(8%或10%)的工资金额。假设参与者每个时刻的工资L(t)是随机的，并服从如下随机微分方程:

σL2(μ(t)dt+dWS(t))

(6)

其中σL1>0和σL2>0是两个波动率因子，分别反映了利率风险和股票市场风险对工资的影响。

1.2 滤波估计

dr(t)=a(b-r(t))-σrdZr(t)

(7)

(8)

(9)

(10)

(11)

其中，Σ(t)=σμρ+m(t)新息过程Z(t)={(Zr(t),ZS(t)),0≤t≤T}定义为

(12)

1.3 模型模糊性

dr(t)=[a(b-r(t))-σrφr(t)]-σrdZQr(t)

(13)

(14)

(15)

(16)

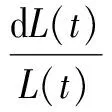
令πS(t)、πB(t)和1-πS(t)-πB(t)分别表示时刻t投资到股票、滚动债券和无风险资产上的财富比例。称随机过程π:={(πS(t),πB(t))}t∈[0,T]为一个投资策略，于是在投资策略π下参与者的养老金账户财富总额Xπ(t)的动态过程为

Xπ(t)θS(t)dZQS(t)+Xπ(t)θr(t)dZQr(t)σs1

(18)

1.4 优化问题

(19)

定义值函数

(20)

为了便于分析，参照Escobar等[13]，假设

其中βi被称为模糊性参数。本文将βS解释为参与者关于股价动态的模糊程度，βr为参与者关于利率动态的模糊程度。

2 模型求解

本节致力于推导优化问题(19)的最优投资策略。

根据动态规划原理，可得值函数(20)满足Hamilton-Jacobi-Bellman(HJB)方程

(21)

定理1对幂效用函数下财富过程为(18)的优化问题(19)，其值函数为

(22)

最优风险敞口为

(23)

最优投资策略π*为

(24)

最坏情形测度Q*由

(25)

决定，其中

注1(仅考虑不完全信息) 如果参与者不考虑模型模糊性，即βS=βr=0，则优化问题(19)退化为一个经典的期望效用最大化问题。此时，值函数为

(26)

最优风险敞口为

(27)

(28)

其中

注2(仅考虑模糊厌恶) 如果参与者可以完全观测金融市场上所有信息，那么参与者接收的所有信息为{Ft}t∈[0,t]。此时估计风险m(t)=0，优化问题(19)在完全信息下的值函数为

(29)

最优风险敞口为

(30)

(31)

(32)

决定，其中

3 数值算例

4 总结

本文构建了不完全信息和模糊厌恶下DC型养老金最优投资问题，利用滤波技术和动态规划原理得到最优投资策略的解析表达式，并利用数值算例对最优投资策略做了敏感性分析，探究了不完全信息和模糊厌恶对最优投资策略的影响。通过对同时考虑不完全信息和模糊厌恶、仅考虑不完全信息、和仅考虑模糊厌恶三种情形下最优投资策略进行比较静态分析，发现不完全信息和模糊厌恶下的最优投资策略最保守;仅考虑不完全信息时的最优投资策略对风险厌恶系数的变化最敏感，考虑模糊性会降低投资策略对风险厌恶系数的敏感性。据此可推断，如果不考虑不完全信息和模型模糊性，参与者可能由于对金融市场过于乐观的估计而采取较为激进的投资策略，从而遭受损失。