毛细水作用下非饱和土压缩过程的微观非连续变形数值分析

李 强 ，李同录 ，李 华 ，沈 伟 ，李 萍 ，张常亮

（1.长安大学地质工程与测绘学院, 陕西 西安 710054；2.黄土高原水循环与地质环境教育部野外科学观测研究站, 甘肃 正宁 745399；3.中国人民武装警察部队工程大学装备管理与保障学院, 陕西 西安 710086）

微结构演化是土体变形破坏的本质，掌握其动态演化规律是深入认识土体宏观变形破坏机制的关键。压汞技术（MIP）、扫描电镜（SEM）、CT扫描系列是当前研究土体微观变形的主要实验技术。一些学者利用MIP或SEM对荷载作用前后的黏土[1]、混合黏土[2]和黄土[3-4]观测发现，荷载主要改变较大的粒间孔隙。但这2种观测技术对土样都有扰动，不能追踪观测荷载作用前后某一位置微结构的具体变化。Yu等[5]结合μ-CT，尝试设计出了微型土样加载装置，观察土样变形过程中颗粒的位置变化。但观察时需暂停加载，将土样取出，因此对土样造成较大扰动。同样的问题也存在于MIP和SEM中。普通CT观测室较大，可以在加载过程中同步观察微结构的变化。利用普通CT对黄土[6]、膨胀土[7]等研究发现，随着荷载的增加，土体孔隙逐渐分布均匀，不规则大孔隙演变成圆形小孔隙，小孔隙不压缩。但普通CT分辨率相对较低，很难捕获到清晰的微结构特征。综合来看，前人对土体变形前后的微结构变化研究较多，认识较深，但对变形过程中微结构演化尚缺乏直接的观测手段，现有的微观试验技术很难克服这一问题。因此，将数值方法引入土的微观结构分析，是目前较为现实的一种途径。

土在微观上是由颗粒构成的离散体系，可以用离散介质力学方法研究其微观力学性质。非连续变形分析方法[8]（Discontinuous Deformation Analysis，DDA）是常用的离散介质力学分析方法之一。该方法起初是用于宏观块体的分析，例如块状结构岩体的滑坡稳定性[9]、围岩变形与破坏[10]和坝基滑移稳定性等[11]。近几年，一些学者初步尝试将DDA扩展到分析土体微观力学性质中。例如张国新等[12]利用规则的多边形块体构建砂土DDA 模型，研究了砂土应力-应变关系；郭培玺等[13]将多边形颗粒随机填充，构建了粗粒料的 DDA 模型，研究粗粒料的力学特性；郭龙骁等[14]通过人为构建干燥黄土DDA模型，模拟了黄土的单向固结试验。然而这些研究都基于原有DDA模型，只考虑了粒间摩擦、咬合等作用，并没有考虑毛细作用的影响。对于非饱和土，毛细作用是基质吸力的主要来源，也是工程问题关注的重点。岩土工程领域也提出一些考虑毛细作用的离散介质分析方法[15-16]，但这些方法一般在相同大小球形或圆形颗粒之间添加一个等大的或者与距离有关的应力表征毛细作用，这很难有效地考虑毛细水分布状态对非饱和土力学性质的影响。

为此，李强等[17]提出了考虑粒间毛细水作用的DDA方法，能够计算不同含水率下的粒间毛细水分布和相应毛细力，可用于模拟静态条件下非饱和土的持水特性。在此基础上，本文考虑进一步扩展该分析方法，将其用于研究荷载作用下非饱和土微结构的动态演化机制。

本文参考黄土骨架粒的大小及形态建立了理想的非饱和土骨架结构模型，并设置自动加载系统，模拟了非饱和土侧限压缩试验。根据模拟结果，分析了压缩过程中孔隙比、吸力和饱和度的变化规律；通过追踪孔隙的演变得到了不同含水率下孔隙的变形特征。

1 土粒间毛细水算法

1.1 算法思路

在非饱和土中，当相互距离较近的颗粒被毛细水黏连起来，将会形成一个相互作用的系统，此系统中包含毛细吸力和表面张力2 个作用力[18]。所以在颗粒间施加毛细力时，关键在于如何将这2个力施加于土粒之间。

为提出该算法，先作以下假设：①只考虑粒间毛细力；②忽略不同颗粒土-水的接触角差异，即所有接触角都相同；③假定体系处于平衡状态，即模型内部没有水力梯度；④土体中的颗粒均为凸多边形。

算法的思路是：先给定含水率ww，假定该含水率下土颗粒之间的毛细水弯液面半径为rw，基于假设①～③，所有弯液面半径都相同，若求得该半径，根据Young-Laplace方程，可计算毛细吸力为：

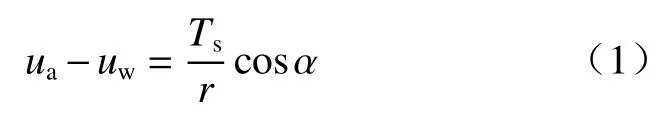
式中：ua——孔隙气压力/kPa；

uw——孔隙水压力/kPa；

Ts——表面张力/（mN·m-1）；

R——弯液面半径/μm；

α——接触角/（°）。

根据毛细水在颗粒上的浸润面积，计算作用在颗粒表面毛细吸力的合力。将该合力与表面张力叠加，嵌入DDA的运动方程组中。

计算某一确定含水率的弯液面半径rw时可用黄金分割法逼近。首先假定弯液面初始半径区间为[a,b]，利用圆心轨迹交汇法分别确定a和b对应的所有土粒之间的弯液面。弯液面和所连接的土粒边界构成封闭的毛细水分布区。统计毛细水分布区的面积，得到与a和b分别对应的毛细水含水率wa和wb。若wb＞ww＞wa，可采用黄金分割法逼近ww。若wa＞ww或wb＜ww，调整半径区间[a，b]的范围，重新求解。最终得出与给定含水率ww对应的毛细水弯液面半径rw。

该方法构建的毛细水分布在颗粒接触或接近的区域，毛细水呈凹透镜状，见图1。在这个透镜形区域内毛细水产生毛细吸力(ua-uw)和表面张力Ts2 个作用力。在二维平面上，将这2个力对土颗粒的作用进行简化。其中，作用在土粒边界上的毛细吸力合力按其作用段分段计算，第i段毛细吸力的作用长度为Li，其合力fsi为：

图1 单颗粒上毛细作用力计算Fig.1 Calculation of the capillary force on the single particle

该力的作用点位于浸湿段中点，方向指向该段的外法线。表面张力Ts仅作用于固、液、气三相交界点处，在温度等条件确定的情况下，其值为常量，方向沿弯液面的切线由两端指向中间。而后分别将2 个力在笛卡尔坐标系下分解到x、y两个方向：(Tsx，Tsy), (fsix,fsiy)，将分解后的力分别以颗粒为单元求和，再嵌入到DDA的运动方程中。

先利用理想模型验证毛细水算法的有效性。构建2 个半径同为10 μm的圆盘，上面圆盘固定，下面圆盘可移动，初始状态下2 圆盘不接触，见图2。分别用理论解和以上算法计算不同间距下的粒间毛细力。

图2 不同水量下两圆盘模型中的毛细水分布Fig.2 Capillary water in the double-disk model at different water content

不考虑圆盘的重力。在二维平面上，当粒间间距为d时，计算不同填充角δ对应的毛细水弯液面半径r[15]：

单位厚度水量Vw为：

粒间毛细力(ua-uw)为：

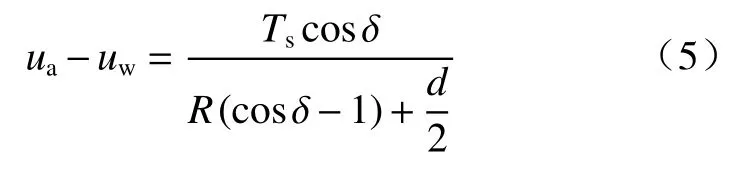
利用式（3）—（5）计算得，间距d为0.50，0.25，0.05 μm的粒间毛细力，计算结果见图3。

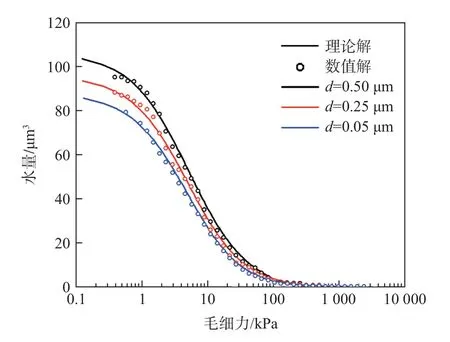
图3 不同间距下的毛细力理论和模拟计算结果Fig.3 Capillary pressure calculated with theory and simulation

毛细力作用的数值模型中，颗粒的重度、接触角与理论计算一致，均设为0，模型所需的其余参数（密度、弹性模量、泊松比、内摩擦角、黏聚力）与表1中的土颗粒一致。该方法计算结果见图3。理论解与模型结果吻合很好，说明毛细作用模型是可靠的，还可将其进一步扩展到土体的微结构演化分析中。

2 非饱和土压缩过程模拟

2.1 骨架结构生成

参考黄土骨架颗粒的形态和大小，建立理想的具有大孔隙结构的非饱和土体微观骨架模型。图4为用于构建模型的实测黄土粒度分布曲线。由图4可知，该土样的骨架大多以粉粒为主，这部分颗粒粒径集中分布在20～30 μm，因此本文只选取该范围粗颗粒建立理想土骨架模型。

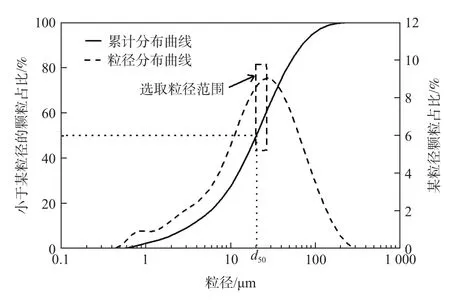
图4 样品粒度分布曲线Fig.4 Particle size distribution curve

通过绘制放大100倍的黄土粗颗粒形状，并用多边形将其拟合，建立黄土粗颗粒形态库。利用落体投放法建立模型，具体步骤为：①建立内径为540 μm×400 μm，盒壁为50 μm的样盒模型；②从颗粒库中随机抽取350个在20～30 μm的颗粒，并将其随机掉落于540 μm×400 μm区域内，形成的微观结构模型见图5（a）。

计算三维模型的孔隙率n3d和孔隙比e：

该模型的初始二维孔隙率n2d为28.0%，孔隙比e为0.390。利用式（6）（7）可以估算出三维孔隙率n2d和孔隙比e分别为48.0%和0.910。

2.2 参数确定

土颗粒和样盒参数见表1。土颗粒一般是物源区岩石风化后的产物，所以密度、弹性模量、泊松比等基础物理力学参数可以参考岩石中（花岗岩）的相应参数。本文旨在探讨毛细作用对土体的影响，没有考虑细粒的作用，黏聚力设为0 kPa。摩擦角根据直剪实验确定。

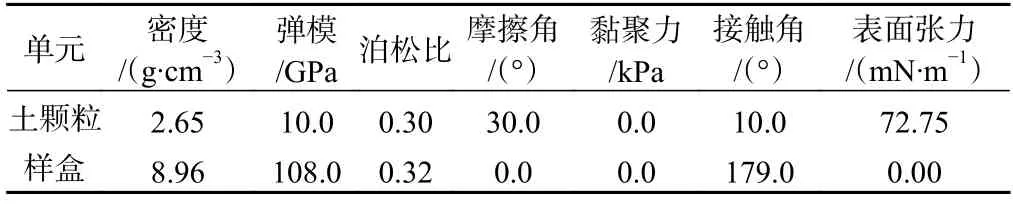
表1 模型参数表Table 1 Parameters in the model

样盒对土样起到约束作用，因此为刚性体，物理参数参考铜的相应参数，如表1。此外，为避免盒壁与土粒的摩擦等非土颗粒间作用力对土体变形的影响，将样盒表面设置为光滑不浸湿，即分别设置内摩擦角、黏聚力为0°，0 kPa，接触角为179°，表面张力为0 mN/m。

2.3 加载系统的构建

骨架模型建立以后，进一步施加毛细作用。构建的模型土样初始含水率为5%、10%、18%。利用毛细水算法确定模型中相应含水率下的毛细水面积及分布范围，并计算出相应毛细力，施加于土颗粒之间。各含水率下毛细水在土中的分布状态如图5（b）—（d），对应的饱和度分别为18.0%、36.0%、68.0%。

加载控制系统的实现方法为：在上述模型上部设置一加载板，加载板向土样逐级加载。加载板与样盒的特性参数、厚度、亲水性均相同，见表1。加载板与样盒之间为光滑接触，只能在竖直方向运动。在加载板上均匀布置4个荷载点，荷载点的间隔为加载板宽度的1/5，用于给土样加载，如图5所示。在加载板上布置3个监测点记录监测点垂直位移，监测点间隔为1/4加载板宽度。

加载控制系统的关键在于如何确定施加下一级荷载的时间节点。实现方法为：首先赋予系统预计施加的各级荷载值，荷载值可任意给定，但需按加载顺序逐级递增。开始加载后，监测点反馈位移信息。在当级荷载下，若监测点反馈的位移量稳定（时步增加100步，位移量小于0.01 μm）且不是最终荷载，则自动施加下一级荷载；若位移未稳定，维持当级荷载，直至稳定；当位移稳定且为最后一级荷载，结束压缩过程。每级荷载作用稳定后，自动输出当级荷载下的土样变形量。本次试验的荷载序列为1 kPa→6.25 kPa→12.5 kPa→25 kPa→50 kPa→100 kPa→200 kPa→400 kPa→800 kPa。

在土颗粒之间增加毛细作用力，结合加载系统，模拟非饱和土侧限压缩试验。在压缩过程中，土颗粒将重新排列，孔隙结构变形，毛细水重新分布。在每一时步，模型将重新计算毛细水弯液面半径及毛细力，并更新荷载矩阵，而后进入下一增量步。同时，模型将实时输出图像，通过图像可直观地观察孔隙结构形态及毛细水分布状态。图6为整个数值试验的计算流程。

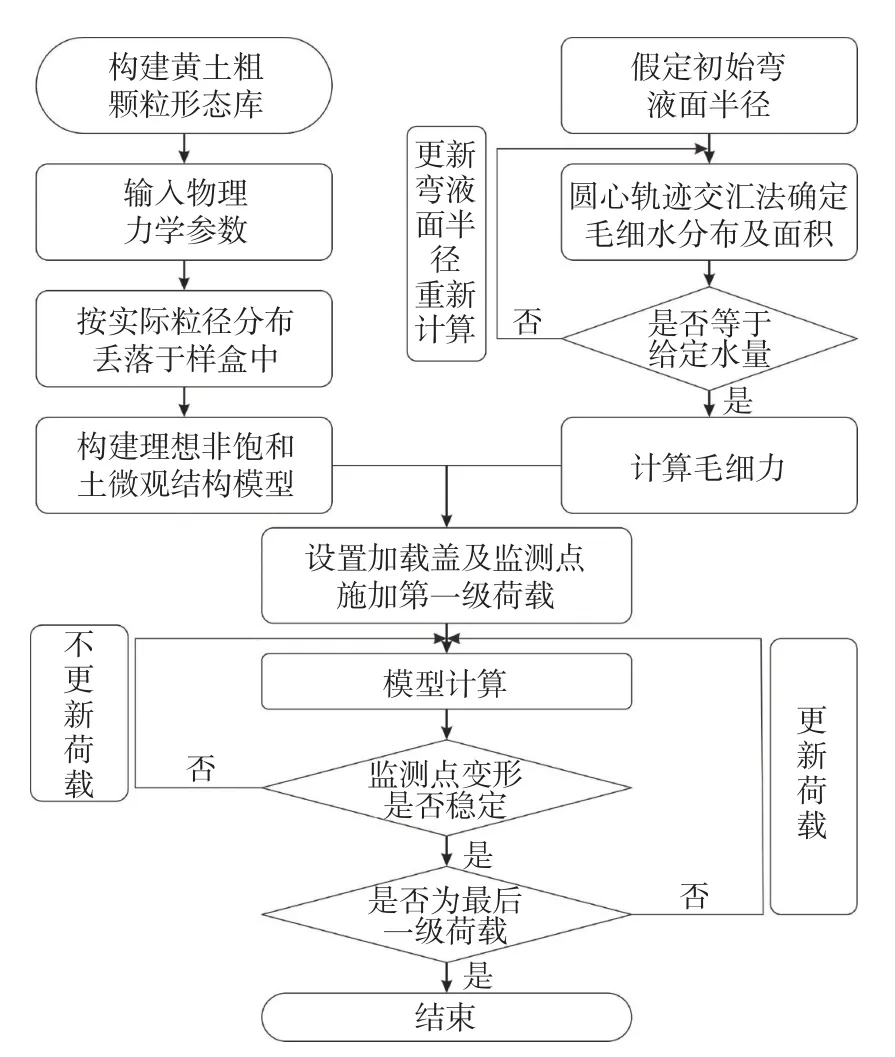
图6 非饱和土压缩试验模拟的计算流程Fig.6 Flow chart of simulation for the unsaturated soil compression test

3 模拟结果分析

3.1 e-lgp压缩曲线

实验过程中测量点的竖向位移即模型土的竖向变形S转换为二维孔隙比e：

式中：e0——初始孔隙比；

H——初始模型高度/μm。

根据式（6）（7）估算出三维孔隙比，三维孔隙比e与竖向荷载p之间的关系曲线（e-lgp）如图7。

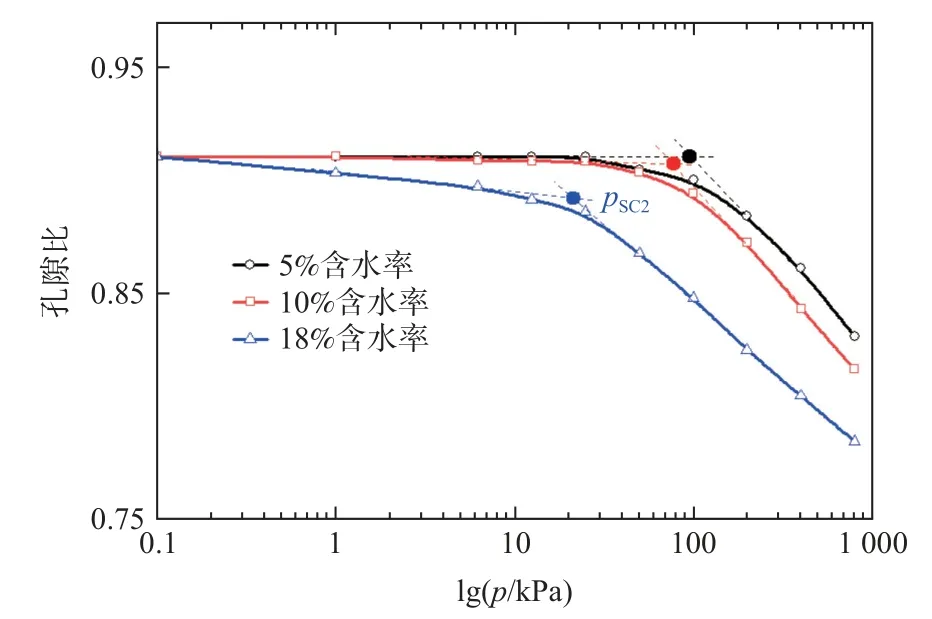
图7 模拟压缩曲线Fig.7 Simulated compression curves

从图7的结果来看，不同含水率下的e-lgp曲线可分为平缓和陡降2个阶段，且含水率高的试样，同一荷载下的孔隙比小。平缓段和陡降段的转折点对应的荷载被称为侧限压缩屈服应力（Psc）[19]，模拟得到的Psc随含水率的增大而减小。这些规律说明基质吸力有利于土体结构稳定，不易发生变形。现有同工况下的试验曲线[20-21]也表现出与模拟结果同样的规律。这说明，数值实验能够反映压缩过程中土体宏观变形特征。

3.2 压缩过程中饱和度和基质吸力的变化

分析在压缩过程中，因颗粒滑移，孔隙变形，引起饱和度和吸力的变化。饱和度Sr和基质吸力ψ随荷载p增加的变化情况见图8。

根据图8，随荷载的增加，Sr-p呈上升趋势，ψ-p曲线呈下降趋势。饱和度Sr的上升幅度随初始含水率的增加而增加。说明土体结构的变形与含水率有关。当含水率相对较低时，土体抵抗变形的能力较强，压缩终止后土体结构变形很小。随含水率的逐渐增加，土样的变形量逐渐增大，这与图7反映的结果一致。

图8 压缩过程中饱和度和基质吸力的变化Fig.8 Variation of saturation and matric suction during compression

对于ψ-p曲线，压缩结束后，各含水率条件下基质吸力ψ降幅均较小，其中10%含水率下的降幅最小。原因在于：基质吸力在压缩过程中受到毛细作用与饱和度2个因素的控制，且这2个因素作用效果相反。随着土样压缩，孔隙半径减小，毛细作用增强，基质吸力增大；另一方面由于孔隙体积变小，饱和度增大，导致基质吸力减小。由压缩曲线（图7）可知，当含水率较低为5%时，压缩终止后，土体的孔隙比，或孔隙体积变化不大，所以毛细作用引起的基质吸力变化不大；而含水率较高为18%时，孔隙体积变化大，但由于土样在18%的含水率下已接近饱和，毛细作用对基质吸力的影响很微弱。因此这2种状态下，毛细作用影响微弱，基质吸力主要随压缩过程中饱和度的增加而减小。当含水率为10%时，毛细作用对基质吸力的增强作用与饱和度对基质吸力的减弱作用都有较大的影响，两者相互抵消，因此基质吸力变化量小于5%与18%的土样。但3种含水率下基质吸力总体呈下降趋势，说明饱和度相较于毛细作用而言，是影响基质吸力的主要因素。

总的来说，随荷载的增加，土样饱和度上升，基质吸力下降，饱和度涨幅随土样含水率增加而增加，基质吸力在土样干燥及近饱和时降幅较大。

3.3 微观结构变形分析

数值模拟可以直观地观察土壤微观结构的变化过程，并可以追踪特定孔隙的在不同含水率状态时的变形过程，这是实验技术难以达到的。图9展示了初始土样（含水率0%）的孔隙分布与5%、10%、18%含水率下压缩终止时的孔隙分布情况。并追踪观察了顶（孔隙a）、中（孔隙b）、底（孔隙c）部3个典型孔隙在不同含水率下的变化。

根据图9，在荷载作用下，土样的变形随含水率的上升有显著增加，且含水率较低时，颗粒接触方式包括大量的点接触和面接触，见图9（a），随着含水率增高，土体在压缩后点接触数量明显减少，以面接触为主，见图9（b）。这说明，含水率越高，土壤越易被压缩。

图9 初始孔隙分布与不同含水率条件下压缩终止时孔隙分布Fig.9 Model pore distribution at the end of compression under different water content

对于上部孔隙a，在土样含水率为5%时，孔隙a在压缩终止时产生了变形，孔隙面积被压缩，但孔壁颗粒位移较小，孔隙仍保持初始形态；含水率增大到10%和18%时，孔隙a均被压扁，孔壁颗粒发生了明显的位移，孔壁坍塌，孔壁颗粒进入孔隙中，孔隙由1个大孔分解成几个小孔隙。

对于中部孔隙b，在土样含水率为5%时，孔隙b未发生明显的变形，孔隙基本维持初始大小和形态；在含水率达到10%时，孔隙b面积被压缩减小，但孔隙形态未发生明显的改变，孔壁未坍塌；当含水率进一步增大达到18%接近饱和时，孔隙b孔壁颗粒发生较大的位移，孔壁坍塌，孔隙分解成多个小孔。

对于底部孔隙c，在土样含水率为5%时，孔隙基本未产生变形；含水率达到10%时，孔隙面积有微弱减小，形态不变；含水率达到18%接近饱和时，孔壁坍塌，孔隙分解成若干个小孔，原始孔隙发生彻底改变。

在压缩时，上部孔隙（孔隙a）在含水率低时即产生变形，随着含水率增大孔隙变形随之增大；中部孔隙（孔隙b）在含水率较小时基本不发生变形，随含水率增大发生变形，接近饱和时孔壁坍塌；底部孔隙（孔隙c）在含水率较低或中等时均很难发生变形，含水率接近饱和时，孔壁坍塌孔隙分解。这说明，在土体压缩时，靠近受压位置的孔隙优先发生变形，远离受压位置的孔隙不易发生变形。曹亮等[22]利用改进的细观结构观测固结仪，观察到了土样变形过程中相似的现象；孔隙的变形形式与水分含量有关，随含水率增大，孔隙变形逐渐由体积收缩变化演变为孔壁坍塌孔隙分解成更小的孔隙。

将土体在压缩过程中的孔隙变形模式概化为图10所示的概念模型，其规律为：在含水率较低的情况下，孔壁颗粒稳定，孔隙以收缩变形为主，如图10（b）。当含水率升高后，孔壁颗粒坍塌进入孔隙内部，以分解变形为主，如图10（c）。Xie等[3]和Wang等[4]通过实测试验对土体压缩过程中孔隙、颗粒形态的统计表明，高含水率下加载过程中，土颗粒会失去稳定，颗粒将重新排列，导致孔隙大小、形态和颗粒方向都发生了变化。这实际上也从侧面证明了土体在高含水率下发生了分解变形，孔壁坍塌，较大的孔隙分解为小孔隙。

图10 不同含水率下孔隙变形的主要形式Fig.10 Main forms of pore deformation under different water content

不同含水率下变形模式的差异本质上与基质吸力有关。基质吸力的存在，增加了土颗粒之间的有效应力，从而增强土颗粒之间的摩擦力，使得土颗粒之间更难发生滑移，利于维持土体结构，土体孔隙以收缩变形为主。基质吸力随含水率的增加而减小，维持土颗粒稳定的能力将随之减弱，土颗粒之间易于滑移，孔隙的变形形式逐渐转为分解变形为主。在基质吸力很低，土体接近饱和时，土样极易发生压缩变形，颗粒极易发生位移，孔隙产生较大变形，土体表现出整体的软化现象，土体强度丧失。

4 结论

（1）根据实际黄土骨架颗粒分布、形状建立了理想非饱和土模型，将毛细力作用施加于土骨架颗粒间，在整个结构上施加外荷载，模拟了非饱和土的常含水率压缩过程。获得的压缩曲线与同工况下的试验结果规律一致，表明本文的数值试验能够反映土体的宏观变形特征，即随荷载增加，孔隙比逐渐减小，并且同一荷载下，含水率越高，土壤的压缩量越大。

（2）对压缩过程中土水作用模拟结果表明，常含水率压缩引起土壤饱和度增大，基质吸力减小。随含水率的升高，饱和度的增幅逐渐增大；基质吸力的下降程度受毛细作用与饱和度2个因素影响，其在干燥与近饱和时降幅较大。

（3）追踪土体特定孔隙的演变过程，结果表明在土体压缩时，靠近受压位置的孔隙优先发生变形，远离受压位置的孔隙不易发生变形；孔隙的变化形式与含水率有关，低含水率时，孔隙主要为体积减小的收缩变形，高含水率时，孔隙主要为孔壁坍塌、孔壁颗粒进入孔隙内部的分解变形。