考虑孔隙水微观赋存形态的非饱和粉土有效应力方程及其验证
2022-07-15曾立峰邵龙潭郭晓霞
曾立峰 ,邵龙潭 ,牛 庚 ,郭晓霞
(1.工业装备结构分析国家重点实验室(大连理工大学), 辽宁 大连 116024;2.大连理工大学工程力学系, 辽宁 大连 116024;3.青岛理工大学理学院, 山东 青岛 266033)
非饱和土的有效应力方程是非饱和土力学的基本方程[1]。对于理论问题而言,非饱和土的有效应力方程是研究非饱和土的强度[2-3]、变形[4]和水-力耦合[5]等问题的基础;对于工程问题而言,基于非饱和土有效应力方程的抗剪强度公式因形式简单,物理意义清晰,已被广泛地应用于求解非饱和土的边坡稳定性[6]、地基承载力[7]和挡土墙土压力[8]等工程问题。鉴于非饱和土有效应力方程在理论和工程问题上的重要性,自20世纪50年代以来,大量的学者从不同的角度提出了众多的非饱和土有效应力方程。其中最具代表性的是Bishop方程[9]:
式中: σ '——非饱和土的有效应力/kPa;

(σ-ua)——净应力/kPa;
(ua-uw)——基质吸力/kPa;
χ——有效应力参数,与饱和度有关,其值介于0~1之间。
后来,部分学者[10-11]认为有效应力参数等于饱和度,在Mohr-Coulomb准则的框架下验证了其对砂土和部分粉土的适用性。另有学者[3,12]认为有效应力参数等于有效饱和度,采用同样的方法验证了其对砂土和绝大部分粉土的适用性。此外,还有学者[13-14]认为有效应力参数等于其它形式的饱和度并且从强度的角度验证了各自的有效性。以上研究极大地推动了非饱和土有效应力方程的发展,然而它们未能较好地考虑孔隙水的微观赋存形态对有效应力的影响,这在一定程度上制约了有效应力方程的适用性。
鉴于以上问题,本文将分析非饱和粉土中孔隙水的微观赋存形态;在孔隙水微观分析的基础上,推导非饱和粉土的有效应力方程;从抗剪强度的角度验证推导的有效应力方程。
1 非饱和粉土中孔隙水的微观赋存形态
一般来讲,非饱和土是由矿物颗粒、水和空气组成的三相系统。然而,由于三相之间存在着极其复杂的物理化学作用,导致非饱和土中矿物颗粒、水和空气已不同于它们各自单独存在时的状态[15]。对于孔隙水而言,在一个非饱和粉土代表性体积单元(representative volume element)中,根据孔隙水的物理、化学和力学性质可以将其分为收缩膜(contractile skin)、吸附水(adsorbed water)和毛细水(capillary water),如图1所示。这3类形态的孔隙水反映了非饱和粉土中孔隙水的微观赋存特性。
1.1 收缩膜
对于非饱和土而言,从力平衡的角度来讲,水-气交界面的具体形态与孔隙水压强、孔隙气压强、水的表面张力及接触角密切相关。当系统平衡后,水-气交界面一般出现在颗粒接触点附近。由于表面张力的存在,水-气交界面会像张紧的弹性薄膜一样将接触点附近的颗粒聚拢在一起,从而增加非饱和土的强度和刚度[16-17]。为了形象地描述水-气交界面的力学作用,常将其称为收缩膜[18],如图1所示。收缩膜对非饱和土力学行为的影响主要取决于收缩膜的多少,而收缩膜的多少可以通过非饱和土中收缩膜的比表面积表征。当土体由饱和状态逐渐变为烘干状态时,收缩膜的比表面积先增大到某一个峰值然后逐渐减小[19]。
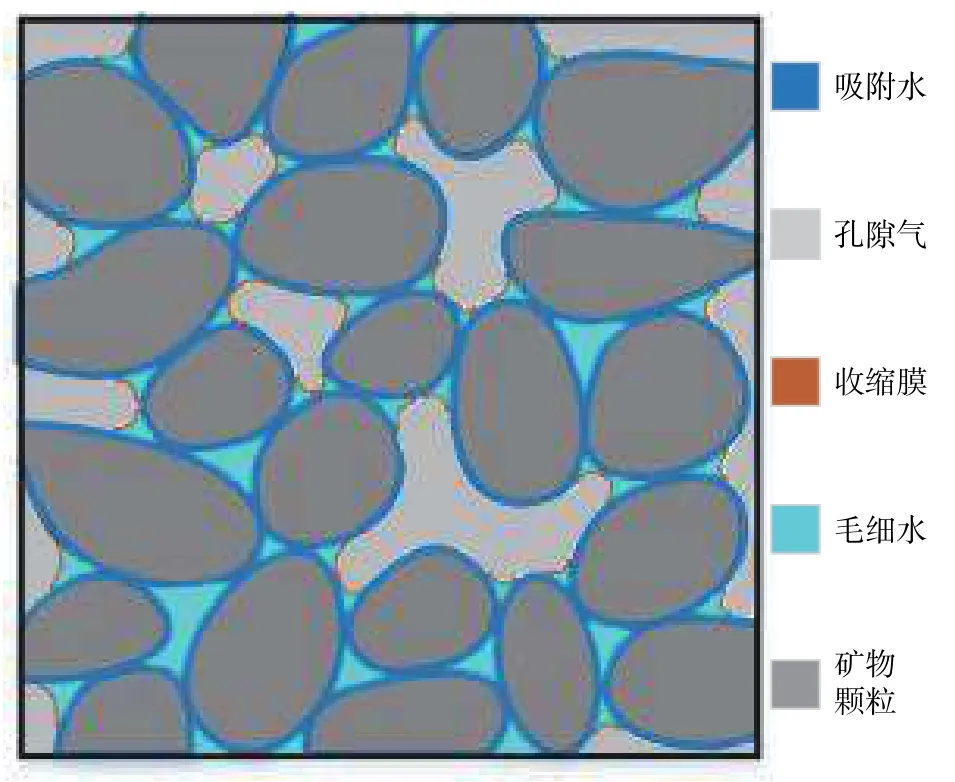
图1 非饱和粉土RVE中孔隙水的微观赋存形态Fig.1 Microstructure of the pore water in an RVE of unsaturated silt
1.2 吸附水
当矿物颗粒与水接触以后,它们之间会形成固-液交界面,其直观的现象是颗粒被一定厚度的吸附水膜包裹。吸附水膜的形成主要源于交界面附近的短程物理化学作用,这种短程作用主要包括电场力作用和范德华力作用[20]。短程物理化学作用使得吸附水的势能显著降低、正压强明显提高。特别地,短程物理化学作用在黏性土中尤其显著,从而导致黏土矿物表面被包裹着较厚的吸附水膜[15]。当土体由饱和状态逐渐变为烘干状态时,矿物颗粒表面的吸附水分子会不断地转换为孔隙气中的水分子和毛细水中的水分子,进而通过孔隙气和毛细水排出土体。因此,吸附水膜的厚度会逐渐减小。当土体处于饱和状态时,吸附水膜的厚度达到最大值;当土体接近烘干状态时,吸附水膜的厚度达到最小值[21]。吸附水对非饱和土力学行为的影响在很大程度上取决于吸附水膜的厚度。
1.3 毛细水
当烘干状态的土体与水接触以后,矿物颗粒表面首先会形成一定厚度的吸附水膜。随着饱和度的增加,颗粒接触点周围会形成互不连通的弯月水,常被称为悬索状毛细水(pendular water)。当饱和度进一步增加时,悬索状毛细水会相互连通,形成纤维状毛细水(funicular water),如图1所示。毛细水的基质势或应力状态主要受水的表面张力、矿物颗粒与水之间的接触角以及矿物颗粒围成的孔隙的几何特性(如孔隙的形状、尺寸、分布及连通性等)控制,在微观上,其可以由Young-Laplace方程表征。当基质吸力大于某一较大值时,毛细水会发生空化,从而使得毛细水逐渐减少直至消失。与吸附水的正压强状态不同的是,毛细水呈现出负压强状态,这种负压强状态有利于毛细水周围的颗粒聚集,从而提高非饱和土的强度和刚度[22]。尽管从微观上看,毛细水具有不同于常规液态水的属性,但是从宏观上看,毛细水仍然呈现出液态水的流动行为。
2 考虑孔隙水微观赋存形态的有效应力方程
2.1 非饱和粉土的扩展三相孔隙介质模型
基于孔隙水微观赋存形态的分析结果,可以得知:位于颗粒接触点附近的收缩膜是一层张紧的弹性薄膜,所以其能够承担并传递荷载;位于颗粒表面的吸附水膜具有一系列不同于常规液态水的独特性质,例如高度规律排列的结构[23]、更高的密度[24]、更大的黏度[25]以及更高的剪切模量[26]。正是由于这些独特的物理力学性质,吸附水膜表现出类似于固体物质的行为,这意味着吸附水可以被视为一种能够承担并传递荷载的结构。与此同时,非饱和土中还存在能够承担并传递荷载的核心结构—矿物颗粒骨架。鉴于收缩膜、吸附水膜(其含量会随饱和度或基质吸力发生变化)和矿物颗粒骨架均能承担并传递荷载,在此将三者组合成一个广义相,称为广义土骨架相(generalized soil skeleton)。于是,广义土骨架、毛细水和孔隙气组成了非饱和土,在此情况下,非饱和粉土可用扩展的三相孔隙介质模型描述,如图2所示。
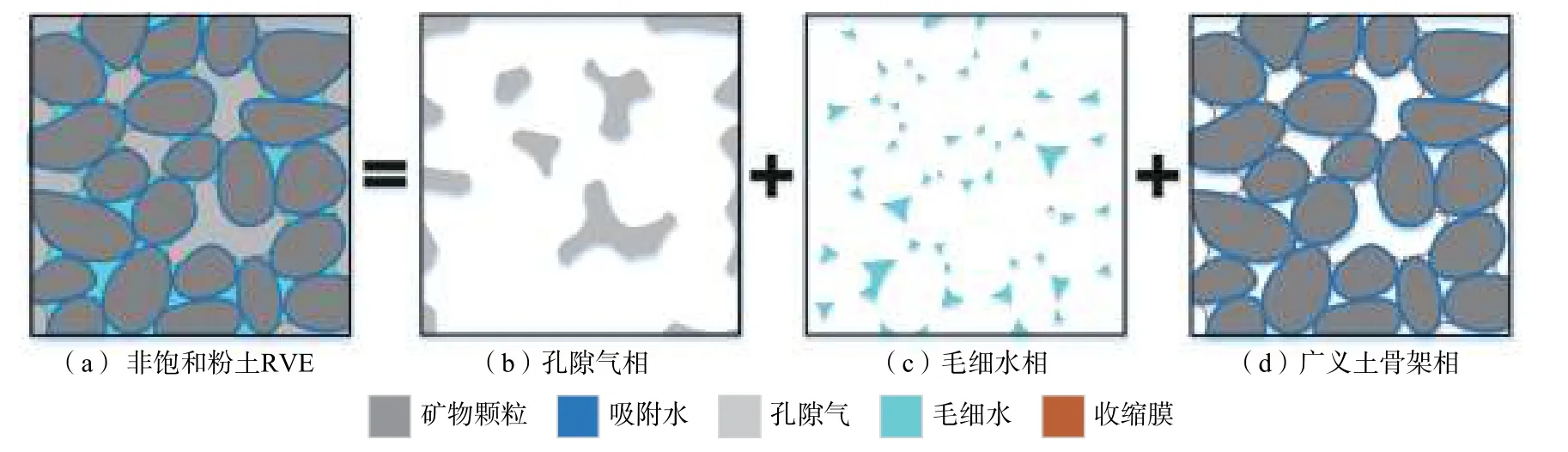
图2 非饱和粉土的扩展三相孔隙介质模型Fig.2 An extended three-phase porous medium model for unsaturated silt
基于扩展的三相孔隙介质模型,在一个非饱和粉土RVE内可以定义一组明确的体积—饱和度关系(图3)。非饱和粉土RVE内各单独相的体积应满足以下关系:
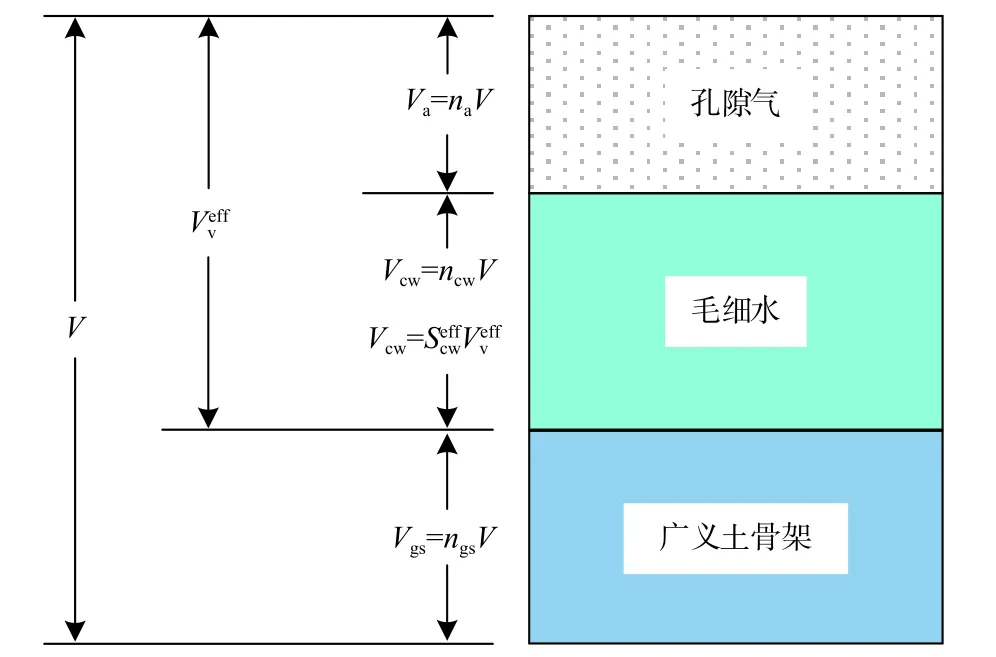
图3 非饱和粉土的扩展三相孔隙介质模型的体积—饱和度关系Fig.3 Schematic diagram of the volume-saturation relations of an extended three-phase porous medium model for unsaturated silt

式中:Va——孔隙气相的体积/m3;
Vcw——毛细水相的体积/m3;
Vgs——广义土骨架相的体积/m3;
V——非饱和粉土RVE的总体积/m3。
非饱和粉土RVE中孔隙气、毛细水和广义土骨架的体积分数可以表示为:
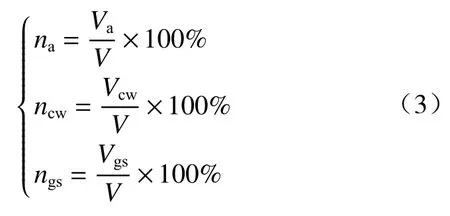
式中:na——孔隙气相的体积分数/%;
ncw—毛细水相的体积分数/%;
ngs—广义土骨架相的体积分数/%。
联立式(2)和式(3),可得:

在扩展的三相孔隙介质模型下,非饱和粉土的有效孔隙体积是孔隙气的体积与毛细水的体积之和:

非饱和粉土的有效孔隙的体积分数(或有效孔隙率)可以表示为:

在此情况下,饱和度的定义应为毛细水的体积与有效孔隙体积之比:

2.2 有效应力方程的推导
在扩展的三相孔隙介质模型建立之后,可以在其基础上采用分相平衡分析法[1]推导非饱和粉土的有效应力方程。
选取一个非饱和土整体微元体并对其进行受力分析,见图4(a)。在此整体微元体中分离出孔隙气相、毛细水相和广义土骨架相并分别分析各单独相的受力情况,见图4(b)—(d)。由于收缩膜已被视为广义土骨架相的组成部分,所以孔隙气相与毛细水相之间并不直接接触,这就意味着孔隙气相与毛细水相之间不存在相互作用力。

图4 非饱和土整体及各分相的微元体的受力示意Fig.4 Illustration for the forces acting on the unsaturated soil, pore air, capillary water and generalized soil skeleton
非饱和土整体微元体的力平衡微分方程为:
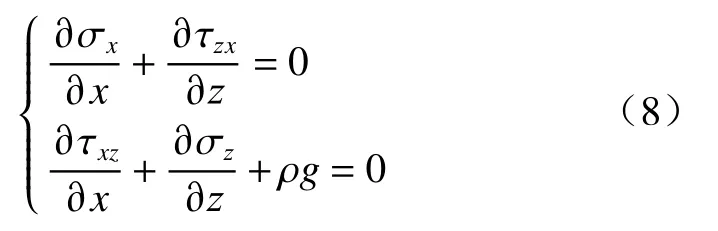
式中: σx、 σz——作用在非饱和土整体微元体上的总正应力/kPa;
τzxτxz、 ——作用在非饱和土整体微元体上的总剪应力/kPa;
ρ——非饱和土的密度/(kg·m-3);
g——重力加速度/(m·s-2)。
孔隙气相微元体的力平衡微分方程为:

式中:ua——孔隙气压强/kPa;
——广义土骨架相对孔隙气相的作用力,其是一种体积力/(kN·m-3);
ρa——孔隙气的密度/(kg·m-3)。
毛细水相微元体的力平衡微分方程:
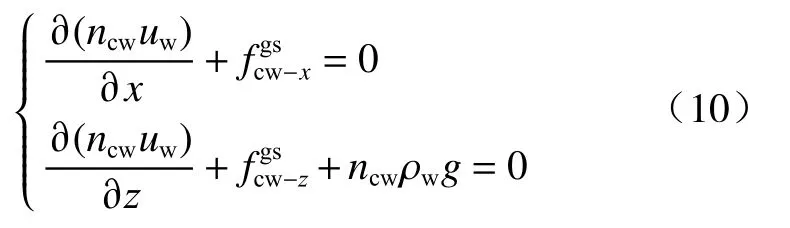
式中:uw——毛细水压强/kPa;
ρw——毛细水的密度/(kg·m-3)。
广义土骨架相微元体的力平衡微分方程:



分开考虑孔隙气压强和毛细水压强作用下广义土骨架相微元体的受力情况,结合式(3)—(7),可以计算得:

将孔隙气相、毛细水相和广义土骨架相微元体的平衡微分方程式(9)—(11)叠加并考虑到以下条件:


3 有效应力方程的验证
3.1 验证思路
本次将从抗剪强度的角度验证有效应力式(13)。在Mohr-Coulomb准则框架下,基于有效应力式(13),破坏面上的抗剪强度式可表示为:

式中: τf——破坏面上的抗剪强度/kPa;
c'——饱和土的有效内黏聚力/kPa
φ'——饱和土的有效内摩擦角/(°)。
有效应力式(13)的验证问题转变为抗剪强度式(14)的验证问题。为了验证式(14),首先需要确定计算毛细水有效饱和度的方法。考察的表达式(7),改写为如下形式:
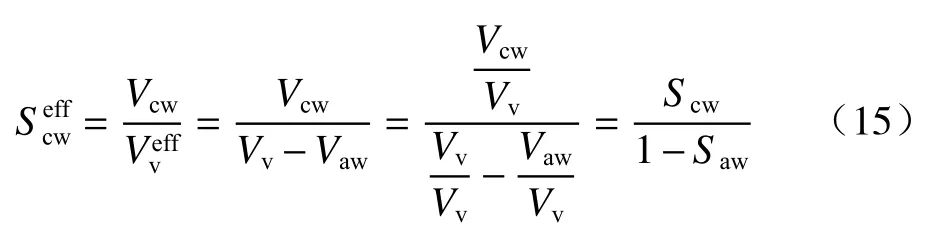
式中:Vaw——吸附水的体积/m3;
Vv——孔隙的体积/m3,Vv=Va+Vcw+Vaw;
Scw——毛细水的饱和度;
Saw——吸附水的饱和度。
根据式(15)可知,当毛细水和吸附水的饱和度随基质吸力的变化规律明确以后,随基质吸力的变化规律即可相应地明确。为此,本文采用了Lu[21]建立的持水特征曲线(SWRC)模型。该模型不仅可以分别量化毛细水和吸附水的饱和度随基质吸力的变化规律,而且也可以考虑空化效应(cavitation)对持水行为的影响,所以其在物理机制上更为合理。这意味着通过Lu[21]的SWRC模型计算的具有更高的精度,该模型的基本思想包括3 个方面:
①非饱和土的饱和度可分为毛细水的饱和度和吸附水的饱和度:

式中:S——非饱和土的饱和度;
ψ——基质吸力/kPa。
②毛细水SWRC方程为:
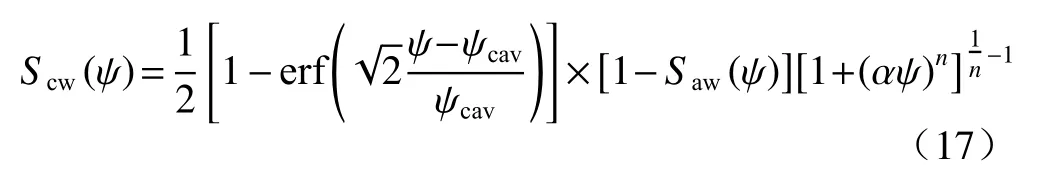
式中: ψcav——平均空化基质吸力/kPa;
α——进气值的倒数/kPa-1;
n——与孔隙尺寸分布相关的参数;
erf( )——误差函数。
③吸附水SWRC方程为:

式中:Saw0——基质吸力为1 kPa时吸附水的饱和度,即吸附水饱和度的最大值;
ψd——烘干状态对应的基质吸力,即基质吸力的最大值,取为106kPa;
l——与吸附作用程度有关的参数。
考虑到砂土和一部分粉土试验数据难以有效地评价不同抗剪强度公式的优劣[27-28],本文从现有文献[29]中选取了一组重塑粉质黏土(成分为20%的Speswhite高岭土、10%的伦敦黏土和70%的HPF4 硅微粉)的试验数据。该数据既包含一组广吸力范围内的SWRC数据,也包含5种不同围压(0,50,100,200,400 kPa)下的抗剪强度数据,这为式(14)的验证提供了较为全面和可靠的试验数据。另外,为了全面地评价抗剪强度式(14)的有效性和合理性,在此也给出了其它2 种通用的抗剪强度公式[10,12]:
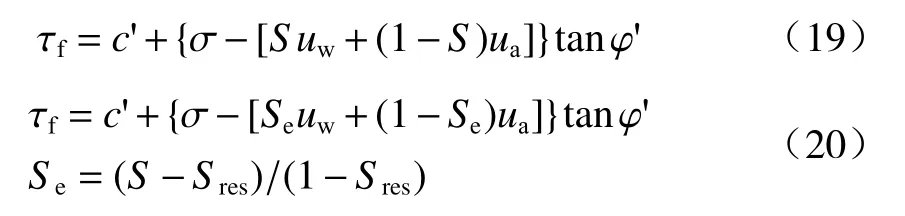
式中:Se——非饱和土的有效饱和度;
Sres——残余饱和度。
饱和度S、Se和Sres的值均由VG模型确定。
3.2 验证结果
图5(a)显示了VG模型和Lu[21]模型关于重塑粉质黏土SWRC数据的拟合结果。从图中可以看出,2种模型对实测数据均具有较好的拟合结果,其中VG模型的拟合相关系数R2=0.990 5,Lu[21]模型的拟合相关系数R2=0.990 8。当基质吸力超过28 MPa时,VG模型预测的饱和度随基质吸力的增加基本保持不变,Lu[21]模型预测的饱和度随基质吸力的增加缓慢减小,直至基质吸力达到最大值106kPa。现有的实测数据[21,30]表明:在高吸力阶段,随着基质吸力的增加,饱和度仍然会不断减小。这就意味着Lu[21]模型更符合实际的物理过程。
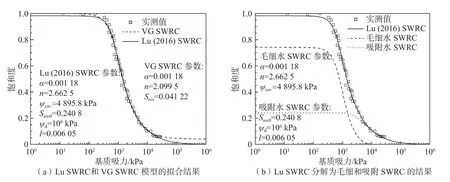
图5 两种SWRC模型的拟合结果Fig.5 Fitting results of two SWRC models
图5(b)显示了Lu[21]模型分解为毛细水SWRC和吸附水SWRC的结果。从图中可以看出,对于毛细水SWRC而言,随着基质吸力的增加毛细水饱和度先大致保持不变;当基质吸力达到800 kPa左右(即进气值附近)时,毛细水开始从土体孔隙中迅速排出,毛细水饱和度相应地迅速减小;当基质吸力达到4 900 kPa左右(即平均空化基质吸力附近)时,毛细水会发生空化现象。随着基质吸力的进一步增加,空化现象会不断地进行。当基质吸力达到10 MPa附近时,毛细水饱和度将趋近于0。然而,由于现有的SWRC模型[14,31]未能较好地考虑毛细水的空化现象,从而导致高吸力阶段毛细水饱和度普遍被高估。对于吸附水SWRC而言,当基质吸力小于4 900 kPa时,吸附水饱和度随基质吸力的增加基本保持不变;当基质吸力大于4 900 kPa时,吸附水饱和度开始迅速减小。当基质吸力进一步增加至43 MPa时,吸附水饱和度开始缓慢减小,直至基质吸力达到最大值106kPa。
图6显示了不同净围压下重塑非饱和粉质黏土的实测抗剪强度及3种抗剪强度公式,见式(14)(19)(20),的预测结果。从图中可以看出,对于实测抗剪强度而言,在相同的净围压下,重塑粉质黏土的抗剪强度随基质吸力的变化规律大致可以分为4 个阶段:①抗剪强度快速增加阶段,此阶段的基质吸力范围约为0~500 kPa(近似饱和阶段);②抗剪强度缓慢增加阶段,此阶段的基质吸力范围约为500~900 kPa;③抗剪强度的峰值阶段,此阶段的基质吸力约为1 000 kPa;④抗剪强度下降阶段,此阶段的基质吸力超过1 000 kPa。与此同时,在相同的基质吸力下,重塑粉质黏土的抗剪强度随净围压的增加而增加。对于重塑粉质黏土的抗剪强度随基质吸力和净围压的变化规律,现有的2 种抗剪强度公式,式(19)(20),未能很好地预测这种变化规律,但是本文提出的抗剪强度式(14)较好地预测了这种变化规律(图6)。

图6 不同净围压下重塑非饱和粉质黏土的3种抗剪强度公式的预测结果Fig.6 Predictions of three shear strength equations for a reconstituted unsaturated silty clay under different net confining pressures
与式(14)相比,式(19)(20)在基质吸力超过500 kPa时严重地高估了重塑粉质黏土的抗剪强度,其中式(19)的高估程度更甚。这主要是因为当基质吸力超过500 kPa时,有效应力参数的大小会显著地影响有效应力和抗剪强度的大小。由于式(19)采用了饱和度S作为有效应力参数,认为毛细水和吸附水均对有效应力有贡献,从而高估了抗剪强度的大小。尽管式(20)通过采用有效饱和度Se分离了部分吸附水,在一定程度上改进了式(19),但仍然高估了抗剪强度的大小。这主要是由于有效饱和度Se中引入的残余饱和度Sres并不能描述吸附水饱和度随基质吸力的变化。与上述不同的是,式(14)采用了毛细水有效饱和度作为有效应力参数,从而合理地区分了毛细水和吸附水对有效应力的贡献,然后借助Lu[21]SWRC模型量化了毛细水和吸附水饱和度随基质吸力的变化规律,最后较为准确地预测了重塑粉质黏土的抗剪强度。
4 结论
(1)微观分析表明,非饱和粉土中的孔隙水可分为收缩膜、吸附水和毛细水。由于收缩膜和吸附水具有类固体的性质,它们可以与颗粒骨架组合在一起形成广义土骨架。因此,非饱和粉土可以用扩展的三相孔隙介质模型(即孔隙气、毛细水和广义土骨架)表征,其为非饱和粉土有效应力方程的推导提供了物理基础。
(2)通过采用毛细水有效饱和度,本文推导的非饱和土有效应力方程较好地考虑了毛细水对有效应力的影响。借助Lu模型,本文较为精确地确定了毛细水和吸附水饱和度随基质吸力的变化规律,这为准确计算有效应力奠定了基础。
(3)在不同的净围压下,当基质吸力超过500 kPa时,现有的2种抗剪强度公式均严重地高估了重塑非饱和粉质黏土的抗剪强度。但是,本文提出的抗剪强度公式较好地预测了不同净围压下重塑非饱和粉质黏土的抗剪强度随基质吸力的变化规律。囿于篇幅,本文仅从不同净围压的角度进行了验证。从不同土类的角度进行验证将是下一步工作的重点。
