带精确时间延迟的单机排序问题
2020-04-08王焕男
王焕男
(三亚学院理工学院,海南 三亚 572022)
1 引言
本研究的问题用三参数分别表示为:1|exactlj,aj=bj=a,lj=ka|∑wjCj,1|exactlj,aj=bj=a,lj=ka|Lmax,1|exactlj,aj=bj=a,lj=ka|∑Uj这3个问题。
关于带精确时间延迟的单机排序问题主要成果有:文献[1]对于1|exactlj|Cmax的一种特殊情况提出一个贪婪算法(greedy heuristic)。文献 [2]对于问题 1|exactlj|Cmax提出一个神经网络算法(Hopfield neural network)。文献[3]研究最小化雷达的空闲时间,他们制定一个单机排序问题的确切延误而不是最小化延误;证明一些特殊的例子是多项式可解的;即使在某些特殊情况下,这个问题仍是强NP-难的;如果所有操作的加工时间相同,这个问题已经是强NP-难的。文献[4]基于离散化的时间跨度问题提出一个拉格朗日松弛算法(Lagrange relaxation algorithm)。文献[5]对于问题1|exactlj|Cmax设计1个3.5的近似算法,2-ε的难近似界,O(nlogn)时间内可解;对于问题 1|exactlj,aj≤bj|Cmax设计一个3的近似算法,2-ε的难近似界,O(nlogn)时间内可解;对于问题1|exactlj,aj≥bj|Cmax设计1个3的近似算法,2-ε的难近似界,O(nlogn)时间内可解;对于问题 1|exactlj,aj=bj|Cmax设计1个2.5的近似算法,2-ε的难近似界,O(nlogn)时间内可解。文献[6]假设在单位加工时间下,证明了对于问题1|exactlj,aj=bj=1|Cmax的近似因子是 7/4(界不能改进),并证明单台机的算法可以在O(nlogn)时间内实现,文献[7]证明这个问题是强NP-难的。
对上述研究综述进行汇总如表1所示。

表1 带精确时间延迟的单机排序Tab.1 Single machine scheduling with precise time delay
文章中的符号定义:
aj—工件j的第一道工序加工时间;caj—工件j的第一道工序完工时间;bj—工件j的第二道工序加工时间;pj—工件j的加工时间;Si—工件j的第一道工序开始时间,即工件的开始时间;sbj—工件j的第二道工序开始时间(sbj=cai+lj);lj—工件j的延误时间;Lj—工件j的误工时间;dj—工件j的工期;wj—工件j的权重;Lmax—工件最大延误时间;Cj—工件j的完工时间;∑Cj—工件总完工时间;wjCj—工件j的加权完工时间;∑wjCj—工件加权总完工时间;Uj—如果Cj≤dj,则Uj= 0,否则,Uj=1;∑Uj—工件的总延误个数。
2 1|exact lj,aj=bj=a,lj=ka|∑wjCj的最优算法
本节主要研究带精确时间延迟的单机排序问题。每个工件记为Jj(aj,bj,lj,wj),目标函数为极小化加权总完工时间。分别考虑以下3种情况:
2.1 1|exact lj,aj=bj=lj=a|∑wjCj的最优算法
当aj=bj=lj=a时,最优排序一定是两个工件一组,先执行两个第一道工序,再相应执行两个第二道工序。工件个数是偶数,机器没有空闲,否则机器存在空闲。工件的完工时间一定是C2n-1=(4n-1)a,C2n=4na(n=1,2,3,…)其中之一。工件的开始时间一定是C2n-1-3a,C2n-3a(n=1,2,3,…)其中之一。
LWF(Longest Weighted first):将所有工件重新排序,使得w1≥w2≥…≥wn,再按照J1,J2, …,Jn的顺序加工工件。
定理2.1.1:LWF是问题1|exactlj,aj=bj=lj=a|∑wjCj的最优算法,如图1所示。
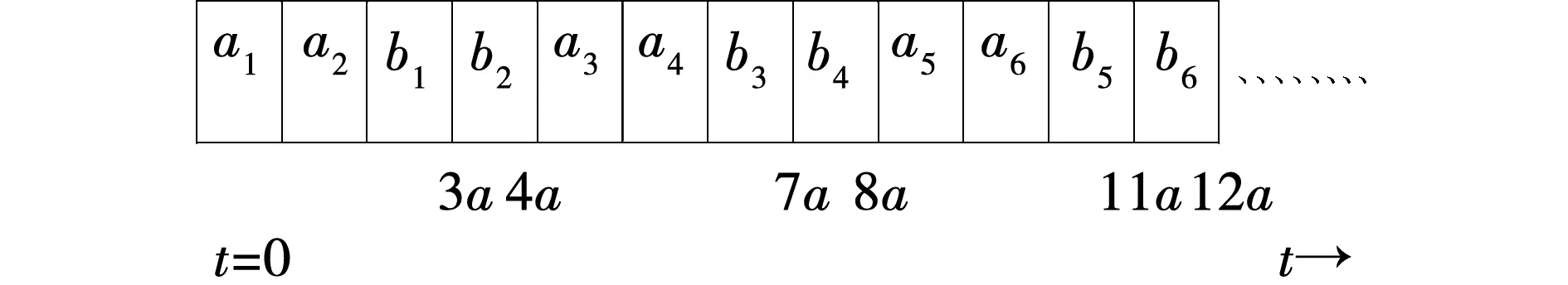
图1 最优排序Fig.1 Optimal sorting
证明:用反证法。假设有一个最优排序,比如σ*违反了WSPT规则,则σ*中一定存在相邻的两个工件Ji和Jk,使得wi ∑wjCj(σ*)-∑wjCj(σ)=wi(Si+pi)+wk(Sk+pk)-wi(Sk+pi)-wk(Si+pk)=(wi-wk)(Si-Sk)>0 即:所得的排序σ目标值比最优值还要小,矛盾! 注:当wj=1时,问题变为1|exactlj,aj=bj=lj=a|∑Cj。 当aj=bj=a,lj=2a时,最优排序一定是3个工件一组,先执行3个第一道工序,再相应执行3个第二道工序。工件个数是3的整数倍时,机器没有空闲,否则机器存在空闲。工件的完工时间一定是C3n-2=2(3n-1)a,C3n-1=(6n-1)a,C3n=6na其中之一。工件的开始时间一定是C3n-2-4a,C3n-1-4a,C3n-4a其中之一。 定理2.2.1:LWF是问题1|exactlj,aj=bj=a,lj=2a|∑wjCj的最优算法,如图2所示。 图2 最优排序Fig.2 Optimal sorting 证明:用反证法。假设有一个最优排序,比如σ*违反了WSPT规则,则σ*中一定存在相邻的两个工件Ji和Jk,使得wi ∑wjCj(σ*)-∑wjCj(σ)=wi(Si+pi)+wk(Sk+pk)-wi(Sk+pi)-wk(Si+pk)=(wi-wk)(Si-Sk)>0 即:所得的排序σ目标值比最优值还要小,矛盾! 注:当wj=1时,问题变为1|exactlj,aj=bj=a,lj=2a|∑Cj。 当aj=bj=a,lj=ka时,最优排序一定是k+1个工件一组,先执行k+1个第一道工序,再相应执行k+1个第二道工序。工件个数是k+1的整数倍时,机器没有空闲,否则机器存在空闲。工件的完工时间一定是C(k+1)n-k=2(k+1)a·(n-1)+(k+2)a,C(k+1)n-(k-1)=2(k+1)a·(n-1)+(k+3)a,…,C(k+1)n=2(k+1)a·n其中之一。工件的开始时间一定是C(k+1)n-k-(k+2)a,C(k+1)n-(k-1)-(k+2)a,…,C(k+1)n-(k+2)a其中之一。 定理2.3.1:LWF是问题1|exactlj,aj=bj=a,lj=ka|∑wjCj的最优算法,如图3所示。 图3 最优排序Fig.3 Optimal sorting 证明:用反证法。假设有一个最优排序,比如σ*违反了WSPT规则,则σ*中一定存在相邻的两个工件Ji和Jk,使得wi ∑wjCj(σ*)-∑wjCj(σ)=wi(Si+pi)+wk(Sk+pk)-wi(Sk+pi)-wk(Si+pk)=(wi-wk)(Si-Sk)>0 即:所得的排序σ目标值比最优值还要小,矛盾! 注:当wj=1时,问题变为1|exactlj,aj=bj=a,lj=ka|∑Cj。 本节主要研究带精确时间延迟的单机排序问题。每个工件记为Jj(aj,bj,lj,dj),目标函数为极小化最大延误时间。分别考虑以下3种情况: 当aj=bj=lj=a时,最优排序一定是两个工件一组,先执行两个第一道工序,再相应执行两个第二道工序。工件个数是偶数,机器没有空闲,否则机器存在空闲。工件的完工时间一定是C2n-1=(4n-1)a,C2n=4na(n=1,2,3,…)其中之一。工件的开始时间一定是C2n-1-3a,C2n-3a(n=1,2,3,…)其中之一。 EDD:将工件重新排序使得d1≤d2≤…≤dn,再按照J1,J2, …,Jn顺序加工。 定理3.1.1:EDD规则可以得到问题1|exactlj,aj=bj=lj=a|Lmax的最优排序。 当aj=bj=a,lj=2a时, 最优排序一定是3个工件一组,先执行3个第一道工序,再相应执行3个第二道工序。工件个数是3的整数倍时,机器没有空闲,否则机器存在空闲。工件的完工时间一定是C3n-2=2(3n-1)a,C3n-1=(6n-1)a,C3n=6na其中之一。工件的开始时间一定是C3n-2-4a,C3n-1-4a,C3n-4a其中之一。 定理3.2.1:EDD规则可以得到问题1|exactlj,aj=bj=a,lj=2a|Lmax的最优排序。 当aj=bj=a,lj=ka时,最优排序一定是k+1个工件一组,先执行k+1个第一道工序,再相应执行k+1个第二道工序。工件个数是k+1的整数倍时,机器没有空闲,否则机器存在空闲。工件的完工时间一定是C(k+1)n-k=2(k+1)a·(n-1)+(k+2)a,C(k+1)n-(k-1)=2(k+1)a·(n-1)+(k+3)a,…,C(k+1)n=2(k+1)a·n其中之一。工件的开始时间一定是C(k+1)n-k-(k+2)a,C(k+1)n-(k-1)-(k+2)a,…,C(k+1)n-(k+2)a其中之一。 定理3.3.1:EDD规则可以得到问题1|exactlj,aj=bj=a,lj=ka|Lmax的最优排序。 本节主要研究带精确时间延迟的单机排序问题。每个工件记为Jj(aj,bj,lj,dj),目标函数为极小化工件总延误个数。分别考虑以下3种情况: 当aj=bj=lj=a时,最优排序一定是两个工件一组,先执行两个第一道工序,再相应执行两个第二道工序。工件个数是偶数,机器没有空闲,否则机器存在空闲。工件的完工时间一定是C2n-1=(4n-1)a,C2n=4na(n=1,2,3,…)其中之一。工件的开始时间一定是C2n-1-3a,C2n-3a(n=1,2,3,…)其中之一。 引理4.1.1:工件集存在不误工的排序且仅当EDD序不误工。 算法H:(1)将工件按照EDD规则排序。(2)计算当前排序中各工件的完工时间,如果已无延误则转(4),否则转(3)。(3)找出第一个延误的工件,比如是第i个工件,则将其删除,得到一个部分排序,返回(2)。(4)将删除的工件以任意顺序排到最后,所得部分排序之后,输出所得排序。 定理4.1.1:算法H可以得到问题1|exactlj,aj=bj=lj=a|∑Uj的最优排序如图4所示。 图4 最优排序Fig.4 Optimal sorting 证明:不妨d1≤d2≤…≤dn。设P=(S,F)为算法所得的排序,其中S为按期完工工件集,F为误工工件集,即算法在第(3)步中删除的工件集合。不妨设F≠Φ,令工件i是算法第一次执行到第(3)步时找到的延误工件,于是i就是算法删除的第1个工件,由算法规则可知 1, …,i-1没有误工工件。下面首先证明:存在最优排序P′=(S′,F′)(S′和F′定义同上),使得i∈F′。设P′=(S′,F′)是一个最优排序且i∈S′。并记F′=π(r+1)…π(n),S′=π(1)…π(r),注意到引理4.1.1,不妨认为dπ(1)≤dπ(2)≤…≤dπ(r)。再由于d1≤d2≤…≤dn,所以一定存在m使得 i∈{π(1), …,π(m)}⊆{1, … ,i},{π(m+1), …,π(r)}⊆{i+1, … ,n}, 并且由i定义,序列1, …,i产生延误,因而{π(1), …,π(m)}≠{1, … ,i}。于是存在1≤h≤i,h∉{π(1), …,π(m)},所以有: {π(1), …,π(m)}∪{h}{i}⊆{1, … ,k}{i}。 由此可知,{π(1), …,π(m)}∪{h}{i}按照EDD排列后不产生延误,且这些工件的总加工时间比{π(1), …,π(m)}中工件总加工时间减少了,这表明在上述工件序列之后加上原来的π(m+1), …,π(r)也不产生误工工件。换句话说,我们构造出了一个误工工件数与P′相同但i是误工工件的排序,即得到了满足要求的最优排序。 根据上面结论,对工件数目作归纳,证明定理结论: 显然,当n=1时,该算法可以得到最优排序。假设算法对工件数为n-1的实例均能找到最优排序,则对任一工件数为n的实例,设P=(S,F)是算法所得的排序,工件i∈F如上定义。所以存在一个最优排序P′=(S′,F′),使得i∈F′,显然有|S|≤|S′|。另一方面,考虑实例{1, …,i-1,i+1, …,n},由归纳假设及算法规则,算法得到的排序形如P=(S,F{i})且是一个最优排序;再注意到P′=(S′,F′{i})是该实例的可行排序,所以又可以得到|S|≥|S′|。因此|S|=|S′|,算法对n个工件的实例也得到最优排序。 当aj=bj=a,lj=2a时,最优排序一定是3个工件一组,先执行3个第一道工序,再相应执行3个第二道工序。工件个数是3的整数倍时,机器没有空闲,否则机器存在空闲。工件的完工时间一定是C3n-2=2(3n-1)a,C3n-1=(6n-1)a,C3n=6na其中之一。工件的开始时间一定是C3n-2-4a,C3n-1-4a,C3n-4a其中之一。 定理4.2.1:算法H可以得到问题1|exactlj,aj=bj=a,lj=2a|∑Uj的最优排序如图5所示。 图5 最优排序Fig.5 Optimal sorting 证明:不妨d1≤d2≤…≤dn。设P=(S,F)为算法所得的排序,其中S为按期完工工件集,F为误工工件集,即算法在第(3)步中删除的工件集合。不妨设F≠Φ,令工件k是算法第一次执行到第(3)步时找到的延误工件,于是i就是算法删除的第1个工件,由算法规则可知 1, …,i-1没有误工工件。下面首先证明:存在最优排序P′=(S′,F′)(S′和F′定义同上),使得i∈F′。设P′=(S′,F′)是一个最优排序且i∈S′。并记F′=π(r+1)…π(n),S′=π(1)…π(r),注意到引理4.1.1,不妨认为dπ(1)≤dπ(2)≤…≤dπ(r)。再由于d1≤d2≤…≤dn,所以一定存在m使得 i∈{π(1), …,π(m)}⊆{1, … ,i},{π(m+1), …,π(r)}⊆{i+1, … ,n}, 并且由i定义,序列1, …,i产生延误,因而{π(1), …,π(m)}≠{1, … ,i}。于是存在1≤h≤i,h∉{π(1), …,π(m)},所以有: {π(1), …,π(m)}∪{h}{i}⊆{1, … ,k}{i}。 由此可知,{π(1), …,π(m)}∪{h}{i}按照EDD排列后不产生延误,且这些工件的总加工时间比{π(1), …,π(m)}中工件总加工时间减少了,这表明在上述工件序列之后加上原来的π(m+1), …,π(r)也不产生误工工件。换句话说,我们构造出了一个误工工件数与P′相同但i是误工工件的排序,即得到了满足要求的最优排序。 根据上面这个结论,对工件数目作归纳,证明定理结论: 显然,当n=1时,该算法可以得到最优排序。假设算法对工件数为n-1的实例均能找到最优排序,则对任一工件数为n的实例,设P=(S,F)是算法所得的排序,工件i∈F如上定义。所以存在一个最优排序P′=(S′,F′),使得i∈F′,显然有|S|≤|S′|。另一方面,考虑实例{1, …,i-1,i+1, …,n},由归纳假设及算法规则,算法得到的排序形如P=(S,F{i})且是一个最优排序;再注意到P′=(S′,F′{i})是该实例的可行排序,所以又可以得到|S|≥|S′|。因此|S|=|S′|,算法对n个工件的实例也得到最优排序。 当aj=bj=a,lj=ka时,最优排序一定是k+1个工件一组,先执行k+1个第一道工序,再相应执行k+1个第二道工序。工件个数是k+1的整数倍时,机器没有空闲,否则机器存在空闲。工件的完工时间一定是C(k+1)n-k=2(k+1)a·(n-1)+(k+2)a,C(k+1)n-(k-1)=2(k+1)a·(n-1)+(k+3)a,…,C(k+1)n=2(k+1)a·n其中之一。工件的开始时间一定是C(k+1)n-k-(k+2)a,C(k+1)n-(k-1)-(k+2)a,…,C(k+1)n-(k+2)a其中之一。 定理4.3.1:算法H可以得到问题1|exactlj,aj=bj=a,lj=ka|∑Uj的最优排序如图6所示。 图6 最优排序Fig.6 Optimal sorting 证明:不妨d1≤d2≤…≤dn。设P=(S,F)为算法所得的排序,其中S为按期完工工件集,F为误工工件集,即算法在第(3)步中删除的工件集合。不妨设F≠Φ,令工件k是算法第一次执行到第(3)步时找到的延误工件,于是i就是算法删除的第1个工件,由算法规则可知 1, …,i-1没有误工工件。下面首先证明:存在最优排序P′=(S′,F′)(S′和F′定义同上),使得i∈F′。设P′=(S′,F′)是一个最优排序且i∈S′。并记F′=π(r+1)…π(n),S′=π(1)…π(r),注意到引理4.1.1,不妨认为dπ(1)≤dπ(2)≤…≤dπ(r)。再由于d1≤d2≤…≤dn,所以一定存在m使得 i∈{π(1), …,π(m)}⊆{1, … ,i},{π(m+1), …,π(r)}⊆{i+1, … ,n}, 并且由i定义,序列1, …,i产生延误,因而{π(1), …,π(m)}≠{1, … ,i}。于是存在1≤h≤i,h∉{π(1), …,π(m)},所以有: {π(1), …,π(m)}∪{h}{i}⊆{1, … ,k}{i}。 由此可知,{π(1), …,π(m)}∪{h}{i}按照EDD排列后不产生延误,且这些工件的总加工时间比{π(1), …,π(m)}中工件总加工时间减少了,这表明在上述工件序列之后加上原来的π(m+1), …,π(r)也不产生误工工件,换句话说,我们构造出了一个误工工件数与P′相同但i是误工工件的排序,即得到了满足要求的最优排序。 根据上面这个结论,对工件数目作归纳,证明定理结论: 显然当n=1时,该算法可以得到最优排序。假设算法对工件数为n-1的实例均能找到最优排序,则对任一工件数为n的实例,设P=(S,F)是算法所得的排序,工件i∈F如上定义。所以存在一个最优排序P′=(S′,F′),使得i∈F′,显然有|S|≤|S′|。另一方面,考虑实例{1, …,i-1,i+1, …,n},由归纳假设及算法规则,算法得到的排序形如P=(S,F{i})且是一个最优排序;再注意到P′=(S′,F′{i})是该实例的可行排序,所以又可以得到|S|≥|S′|。因此|S|=|S′|,算法对n个工件的实例也得到最优排序。 主要研究了带精确时间延迟的单机排序问题。每个工件Jj(j=1,2,…,n)有两道工序aj、bj,第一道工序先于第二道工序加工,第一道工序的完工时间caj与第二道工序的开始时间sbj之间存在一个确切延误时间exactlj,即sbj=caj+lj。所有工序操作时间都相等aj=bj=a(j=1,2,…,n),且确切延误时间是工序操作时间的整数倍lj=ka(k∈N+ )。所有工序在一台机器上执行。分别以极小化加权总完工时间,最大延误和总延误数为目标函数,设计了最优算法。 需要进一步研究和考虑的问题还有: (1)1|exactlj|∑wjCj带确切延误的单机排序问题,目标是加权总完工时间。 (2)1|exactlj|Lmax带确切延误的单机排序问题,目标是极小化最大延误时间。 (3)1|exactlj|∑Uj带确切延误的单机排序问题,目标是总延误数。2.2 1|exact lj,aj=bj=a,lj=2a|∑wjCj的最优算法
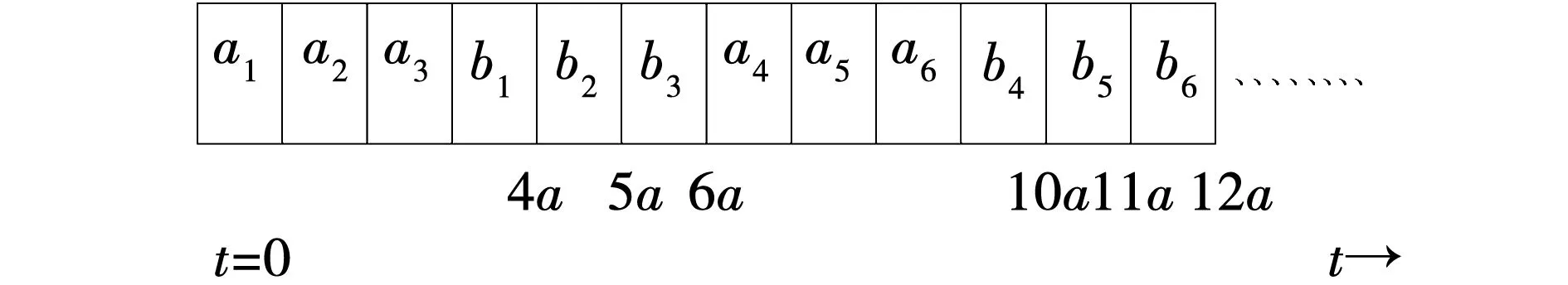
2.3 1|exact lj,aj=bj=a,lj=ka|∑wjCj的最优算法
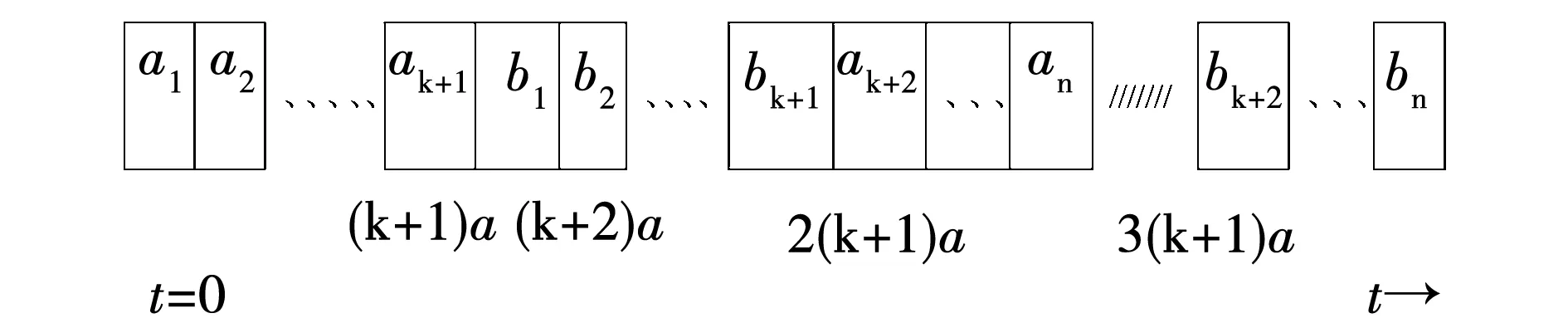
3 1|exact lj,aj=bj=a,lj=ka|Lmax的最优算法
3.1 1|exact lj,aj=bj=lj=a|Lmax的最优算法
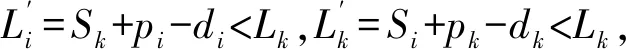
3.2 1|exact lj,aj=bj=a,lj=2a|Lmax的最优算法
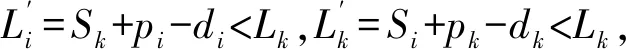
3.3 1|exact lj,aj=bj=a,lj=ka|Lmax的最优算法
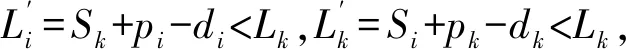
4 1|exact lj,aj=bj=a,lj=ka|∑Uj的最优算法
4.1 1|exact lj,aj=bj=lj=a|∑Uj的最优算法

4.2 1|exact lj,aj=bj=a,lj=2a|∑Uj的最优算法

4.3 1|exact lj,aj=bj=a,lj=ka|∑Uj的最优算法

5 结语
