集成式工艺规划与车间调度的研究综述
2022-07-15刘齐浩李新宇李全俊
高 亮,刘齐浩,李新宇,李全俊
(1.华中科技大学 机械科学与工程学院,湖北 武汉 430074;2.中国兵器装备集团自动化研究所有限公司 智能制造事业部,四川 绵阳 621000)
“中国制造2025”是我国制造强国战略的第一个十年行动纲领,其核心是智能制造。实现智能制造的关键一步是实现制造系统的智能化。制造系统的高效运行能提高企业的竞争能力与对市场的快速响应能力,对于企业乃至国家制造战略层面的发展至关重要[1]。但我国制造系统的效率明显低于国外先进水平,其运行优化技术是主要瓶颈之一。制造系统的运行优化一直是机械制造学科的研究热点。资料表明,制造系统中非切削过程的时间占比较大[2]。车间调度是指在企业车间有限资源的约束下,确定工件在相关设备上的加工顺序和开始加工时间,以保证所选定的生产目标最优。调度是制造系统的基础,是提高制造系统效率的关键技术之一。因此,制造系统运行优化中的调度技术直接影响着制造的效率与成本,与其相关的研究具有重要的实际工程意义。
随着车间信息化能力的增强,各制造子系统之间的关联程度也相应提升,为工艺规划与车间调度的集成提供技术保障[3]。传统的工艺规划与车间调度在制造系统中通常独立运行,相互之间不存在优化配合。将两个制造子系统进行集成,能有效地提高生产效率和提升产品质量。集成式工艺规划与车间调度(integrated process planning and scheduling,IPPS)的集成优化技术能够在工艺规划执行的同时,考虑制造车间的机器状态、制造资源和订单交货期等约束条件,生成更符合调度环境的工艺路线,能够进一步推进制造系统的智能化。
IPPS作为一类典型的NP (non-deterministic polynomial) 难问题,广泛存在于化工、冶金、航空、航天等制造领域中,具有重要的研究意义和工程价值[4]。本文在2011年本团队所发表IPPS综述研究的基础之上[5],主要对近十多年来的相关研究工作进行系统综述与回顾。
1 集成式工艺规划与车间调度问题概述
1.1 工艺规划问题概述
工艺规划是产品设计与制造的桥梁,能将产品设计数据转化成制造信息。通过合理优化工件的工艺路线,能有效提升生产效率、降低生产成本、节省生产资源,在有限的资源及加工能力范围内,满足设计规格和需求。一个成熟的工艺规划系统一般应具有但不限于如下功能,包括检索标准工艺文件、选择加工方式、规划加工路线、选择和分配加工资源(机床、刀具、量具和夹具等)、优化工艺参数、计算加工时间和加工成本、确定工序尺寸和公差及选择毛坯、生成工序图或工序卡等[6]。其中,选择加工方式、规划工艺路线、分配加工资源等功能,可以看作是广义的工艺规划内容,是工艺规划系统的核心功能。
通常情况下,工艺规划问题可以被描述为一个待加工工件的加工过程包含一定数量的加工特征,特征之间存在特定的优先关系约束;不同特征可由不同的工序或工序集合完成加工,一个工序的加工存在多台加工机器可选;工艺规划的任务是在遵循特定的优先关系约束的前提下,合理安排工序的加工顺序及分配对应的加工机器,规划出一条满足特定加工需求的最优工艺路线[7]。
工艺规划需要决策的子问题一般包括加工工艺选择、加工资源选择和工序加工序列确定。与3类子问题相对应的是3种加工柔性:不同的加工特征通过不同的加工工序或工序集合实现,可称为工艺柔性;在满足特定先后约束的前提下,加工工序相互之间的顺序可调,称为工序次序柔性;同一工序的加工有多台机器可选,即机器选择柔性。
1.2 车间调度问题概述
车间调度问题可以描述为将n个工件安排在m台机器上加工,每个工件的加工由若干个工序实现,工件在若干台机器上加工;在遵循一定的工艺约束情况下,将各工件合理地安排到各机器,并决策工件的加工次序和加工开始时间,满足特定的生产目标或需求。一个调度问题可以由三元组α|β|γ描述,α为机器环境,β为加工特征及约束,γ为优化目标。根据α的类型,可以将车间调度问题分为如下类别[8]。
1) 单机调度问题 (single machine scheduling problem,SMP):单机调度问题是所有调度问题中最基础和最简单的,是其他复杂调度问题的特例。其特征为所有工件只有一道加工工序,生产系统中只有一台加工机器,所有工件都在该机器上加工。
2) 并行机调度问题 (parallel machine scheduling problem,PMP):加工系统中有若干台加工功能相同的机器,所有待加工工件只有一道工序,工件可选任一机器执行加工。并行机调度问题可根据机器加工速度的不同,分为并行同速机调度和并行异速机调度。
3) 流水车间调度问题 (flow shop scheduling problem,FSP):n个工艺路线相同的工件,在m台机器上串行加工,需要决策各机器上工件的加工次序[9]。若存在至少某一阶段有多台加工机器可选,则该问题被称为混合流水车间调度问题 (hybrid flow shop scheduling problem,HFSP) 或柔性流水车间调度问题 (flexible flow shop scheduling problem,FFSP)。
4) 作业车间调度问题 (job shop scheduling problem,JSP):n个工艺路线不同的工件,在m台加工功能各异的机器上加工,需要决策各工件的开始加工时间和各机器上工件的加工次序。若存在至少某一工件的工序有多台加工机器可选,则该问题被称为柔性作业车间调度问题 (flexible job shop scheduling problem,FJSP)。
5) 开放车间调度问题 (open shop scheduling problem,OSP):n个待加工工件的加工工序给定,但工序间的加工次序未定,在m台机器上多次加工,需要决策各机器上的工序次序与工序的开始加工时间[10]。
加工特征及约束β主要包括顺序相关的准备时间、加工中断、优先约束、机器故障、机器适用限制、阻塞、零等待等。而优化目标 γ通常包括最大完工时间Cmax、最大流经时间Fmax、最大推迟完成时间Lmax、最大拖后时间Tmax等。
根据实际生产需求和制造环境,车间调度还具有多目标、不确定、动态等特性,给问题带来了更大的求解难度。车间调度已经被证明是NP-Complete组合优化问题,问题可行解的数量随着问题规模的增大呈指数级增长[8]。问题较高的求解难度吸引了大量的研究者寻求快速高效的求解方法。从20世纪50年代开始,国内外的学者们尝试了各种类型的方法对调度问题进行求解。早期这些方法主要是以运筹学为基础的精确算法,包括割平面法 (cutting plane method)、分支定界法 (branch & bound) 等[8]。但是精确算法受限于问题规模,无法在较大规模的调度问题中展现出优势,反而是近似求解方法在20世纪80年代以后成为了当前调度问题求解方法的主流。包括元启发式算法,如遗传算法 (genetic algorithm,GA) 等,以及优先调度规则等方法,在调度问题的求解上展现了足够的优势,逐渐成为当前研究者们求解调度问题的主要手段。到目前为止,新的启发式或元启发式算法的提出和改进,仍然是当前车间调度领域的主要研究方向。
1.3 IPPS问题概述
传统的工艺规划和车间调度是分步进行的。在既定的工艺上进行调度,意味着工艺部分不能给调度提供柔性支持。这会导致某些生产问题,如机器载荷分布不均、瓶颈资源的分配不当、矛盾目标之间优化冲突等。为了解决上述问题,近年来,越来越多的学者提出将工艺规划和车间调度进行集成优化,来寻求更好更高效的制造方案。工艺规划与车间调度的集成逐渐成为当下研究的热点与趋势。
IPPS问题由工艺规划和车间调度两部分组成。与各子问题相比,IPPS问题具有更大的求解难度。其包含的3类柔性分别为工艺柔性、次序柔性及机器柔性。在以上3种柔性确定的前提条件下,车间调度部分可看作是传统的JSP,需要做的决策为对不同工件的工序进行调度。IPPS问题作为工艺规划与车间调度的集成,需要同时决策4类子问题,包括不同工件的工序排序、相同工件工序排序、加工机器选择、工艺选择。这一点不同于任一基础的车间调度类型——FSP、JSP、FJSP。IPPS问题以及各类型调度问题包含的柔性如图1所示。从图1中可以看出,IPPS包含的柔性最多,需要做的决策最多,是最复杂和最难以求解的基础调度类型。
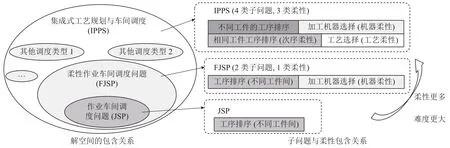
图1 IPPS问题与其他基础车间调度问题的关系Figure 1 The relationship between IPPS problem and other basic shop scheduling problems
根据前文对工艺规划和车间调度的问题概述,可将IPPS的问题描述如下。n个工艺待定的工件,需要在m台具有加工柔性的机器上完成加工;IPPS的任务是在满足特定的约束和优化目标的前提下,为这些工件制定合理的加工工艺路线和车间调度方案。相比于车间调度问题,IPPS问题需要在调度之外为每个工件制定工艺路线。待定工艺的工件需要从网络图中规划生成工艺路线。以图2为例,网络图由5种类型的节点组成:起始节点,表示零件生产过程的开始;终止节点,表示零件生产的终止;工序节点,表示加工工序;OR节点与JOIN节点的组合,代表工件的工艺柔性。工序节点包含3种类型的信息:实心圈中的工序号,{}中的可选机器号,以及[]中对应的加工时间。网络图中的节点由箭头连接,表示工序之间的优先关系约束。需要注意的是,生成工艺路线时,只能选择包含在一对OR节点和对应的JOIN节点间的其中一条工序支路。所选支路所包含的工序和其他工序构成了该工件的可行加工工序组合。此外,每道工序只能选择一台机器作为平台进行相应的加工。以图2为例,其中一条完整可行的工艺路线为1(3)→2(5)→3(2)→6(7)→5(8)→7(13)→9(11)→10(13)。括号外的数字表示工序号,括号内的数字表示机器号。不同的工件具有不同的工艺网络图,一个待加工工件会衍生出相当数量的工艺路线。
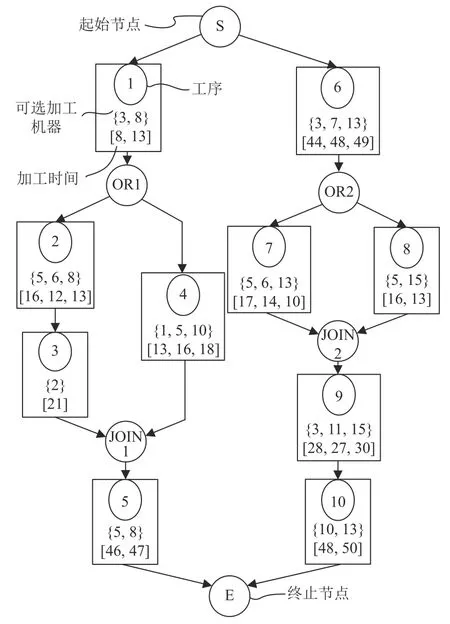
图2 工件工艺网络图Figure 2 The process network graph
2 集成式工艺规划与车间调度问题的研究现状
2.1 工艺规划问题的研究现状
工艺规划的研究方法主要分为精确方法和近似方法两类。其中,精确方法包括数学规划法和分支定界法;近似方法主要包括以GA、蚁群算法 (ant colony optimization,ACO) 在内的诸多智能算法。精确方法能够有效求解小规模问题的最优解,但是随着问题规模的增大,组合爆炸导致的计算效率低下,使得精确方法在求解大规模工艺规划问题中未能展示出足够的优势。相比于精确算法,近似算法更贴合生产实际:实际生产中需要在可接受计算时间内得到近优解,对于问题的最优解则不给予过多关注。
1) 精确求解方法与数学规划模型。
从问题的数学规划模型出发对问题展开研究,有助于加深研究者对问题特征的理解。当前,大多数文献都是基于工艺特征的方式对工艺规划问题进行建模。这种方式会对工件的工艺信息进行整合处理,且在某种程度上使得工件原始的加工工艺信息发生改变[11]。此外,一些文献中的其他建模方式需要对模型进行繁杂的预处理,如将所有可选的工序进行组合,以消除OR节点[12]。这种组合的方式虽然能完整表达工序间的优先关系,且不添加任何额外约束,但是其预处理操作较为繁杂。当OR节点较多或者OR节点间相互包容、拓扑结构复杂时,这种预处理操作会对研究者造成较大的工作负担。Floudas等[13]根据时间表示方式的不同,详细分析了几种工艺规划混合整数规划模型,并提出几类优化方法以提升模型的计算效率。考虑工艺规划与调度的互补性,Li等[14]建立了集成工艺规划与车间调度的数学模型。Xia等[15]为可重构工艺规划问题提出基于特征的零件种类表示模型。同样是基于特征,Jin等[16]建立考虑运输时间的工艺规划问题的混合整数规划模型。
由于精确方法求解工艺规划问题的效率较低,所以当前相关研究较少。早期研究中,Kusiak等[6]用整数规划法尝试求解了工艺规划问题,但是仅局限于较小规模的问题实例。在注塑模具的实际工艺规划中,Gan等[17]提出的一种分支定界方法成功优化并求解动态的工艺规划问题。对于具有柔性工艺规划路线的生产调度问题,Jiang等[18]应用数学规划法,求解以最小化生产到期日绝对偏差和完工时间为优化目标的调度问题。
2) 近似求解方法与启发式。
工艺规划属于NP-Complete问题[19],仅仅利用传统的梯度下降法、图论法和仿真方法很难得到令人满意的优化结果[20]。因此,国内外众多研究学者选择通过智能算法来求解工艺规划问题,其方法主要包括多代理系统 (multi-agent system,MAS)[21]、GA[22]、禁忌搜索 (tabu search,TS)[23]、模拟退火 (simulated annealing,SA)[24]、粒子群优化 (particle swarm optimization,PSO)[25-26]、ACO[27]等。上述智能算法及其混合算法在工艺规划问题的求解中展现了一定的优越性,并在实际案例的应用中取得一定成效。
工艺规划问题可被看作为受约束的旅行商问题(traveling salesman problem,TSP)[28]。为了解决较为复杂的柱状零件的工艺规划问题,Li等[29]提出了一种GA和SA的混合算法。根据可选工艺路线之间的汉明距离 (hamming distance) 来搜索和选择解,混合的SA算法加强了混合算法的邻域搜索能力。Hua等[30]提出了一种基于GA的综合算法,求解工艺规划问题中机器方案选择和工序序列的全局或近全局最优解。Li等[31]提出一种基因编程 (genetic programming,GP) 算法,对工艺信息网状图中的OR节点分支进行遗传操作。与传统的GA相比,GP算法展现了一定的优越性,但是其将网状图转换成树状图的预处理操作难度会随网状图拓扑结构复杂化而增大。Shin等[32]考虑刀具选择和进刀方向等制造资源,提出共生进化算法 (symbiotic evolutionary algorithm,SEA),同时对机器负载平衡、最小化零件转移和最小化刀具更换3个目标进行优化。通过将PSO算法离散化,Wang等[25]提出一种混合了两类局部搜索策略的PSO算法来求解工艺规划问题。随后Li等[33]也提出一种改进的PSO算法,对考虑准备时间的工艺规划问题进行求解,虽未考虑刀具选择和进刀方向,但其算法的效率与其他算法相比仍展现了一定的优势。在文献[34]中,ACO算法结合问题的约束矩阵和状态矩阵,在两个柱状零件的工艺规划问题中得到应用,对比于传统的TS算法、SA算法和GA,该算法的求解效果更好。
2.2 IPPS问题的研究现状
早期的研究者们将工艺和调度分开进行讨论,会在实际生产中导致严重的瓶颈问题,如载荷分布不均、优化目标冲突等。Nasr等[35]和Kim等[36]较早开始尝试将工艺规划与作业车间调度集成。从此,集成式工艺规划与车间调度走进了研究者的视野。工艺规划与车间调度的集成相关研究最早开始于20世纪80年代中期。早期的集成仅是通过增加可选工艺路线数量,以提升制造系统的柔性。而后随着动态反馈思想的引入,使得两系统的集成进一步提升。发展至今,IPPS问题可以根据集成形式大致分成两类:第1类是每个工件具有多条预先生成的工艺路线,调度集成工艺的任务是从这些工艺路线中选择一条进行调度[37];第2种则是每个工件的工艺信息以特征表 (feature table) 或网络图 (network graph) 的形式表示,IPPS需要从图或表中规划得出工艺路线再进行调度。
第1种形式的IPPS问题相对第2种类型更简单,因为通常情况下工件的候选工艺路线数是有限的。Jain等[38]尝试求解车间生产中有多重工艺路线可选的车间调度问题。Chan等[39]提出带支配基因的GA(GA with dominant genes,GADG) 来解决柔性制造系统 (flexible manufacturing system,FMS) 中具有可选工艺路线的调度问题。Li等[14]建立第1种类型IPPS问题的数学模型,并提出相应的进化算法进行求解。Shen等[40]研究分布式制造系统中的IPPS问题,提出基于代理智能体 (Agent) 的求解思路,启发了后续的相关研究。随后,Li等[21]又提出基于代理智能体的方法来集成工艺规划和调度,并通过实验证明代理智能体之间的交互和沟通在解决IPPS问题中的有效性。Özgüven等[41]在FJSP的基础上,建立第1种类型IPPS问题的混合整数线性规划 (mixed-integer linear programming,MILP) 模型。在供应链的IPPS问题中,Moon等[42]同样建立了一个MILP模型来描述问题中的集成,并提出一种基于拓扑排序的进化算法来求解该类IPPS问题。
由于第1种形式的IPPS问题中,每个工件的待选工艺路线有限,本质上还是属于FJSP。因此,近十年IPPS研究的焦点逐渐转移到了第2种类型上。第2种类型IPPS问题的工件工艺信息,通常有两种表达方式:特征表和网络图,两种表现形式可以互相转换。Li等[20]提出一种SA算法来求解该类IPPS问题,并通过最大完工时间、机器利用率、工件总拖期和制造成本这4个目标来评价所提算法的优越性。Leung等[43]将ACO算法应用于多Agent系统来求解IPPS问题。针对第2种类型的IPPS问题,Jin等[44]对多个MILP模型进行了分析讨论,并在线性求解器上对这些模型进行了求解。第2种类型最著名的数据集为Kim数据集[45],许多研究都是基于该数据集开展的。Li等[46]提出一种新的混合算法对Kim数据集进行了求解,与Kim等[45]的算法相比,刷新了大部分结果。Zhang等[47]提出一个加强的ACO算法,对Kim数据集进行求解,并刷新了24个问题中的17个。Li等[48]随后提出一种变邻域搜索遗传算法(genetic algorithm and variable neighborhood search,GAVNS),再次刷新了该数据集中的9个解,其中3个解达到了下界。Lian等[49]提出的殖民竞争算法进一步刷新Kim数据集,取得了更好的结果,成功找到全部下界。
现在有关于IPPS的精确方法和数学模型的研究较少。基于逻辑的Benders分解 (logic-based benders decomposition,LBBD) 算法,Barzanji等[50]开发了几种分解方式,作为解决IPPS问题的精确求解方法。Li等[14]建立基于工件工艺路线的IPPS数学模型,并提出一种进化算法对问题进行求解。关于IPPS问题模型最系统的研究是Jin等[44]于2016年开展的,在研究中分析了几类MILP模型,并且在线性求解器CPLEX中进行求解,以比对它们的求解效率。但是,对于当前大部分的大规模IPPS问题实例,现有的IPPS模型都无法进行求解。受限于问题规模,现有主流的线性求解器求解模型时,获得可行解的求解时间过长,甚至在较长时间内都无法得到一个可行解。
从问题类型角度出发,第2种类型的IPPS问题更符合先进制造系统的现状,因为特征表和网络图的工艺表现形式能够给予调度系统更多的支持。从问题的求解方法出发,当前无论是第1种类型的IPPS问题还是第2种类型,主流求解算法都属于近似求解方法,如启发式规则、GA、SA算法、TS算法、PSO算法、ABC算法等。由此,可以推断出未来短期内IPPS问题的主流研究方向,仍然是改进各类型求解算法以获取第2种类型IPPS问题更好的求解效果。
3 多目标IPPS问题的研究现状
为解决实际生产中的多目标问题,并为生产管理决策者提供高质量的替代方案,实际的IPPS问题同样可以作为多目标优化问题存在。常见的优化目标包括最小化最大完工时间、最小化总机器负荷和最小化最大机器负荷等。多目标IPPS问题的常用处理方法有基于权重的方法和基于Pareto的方法。由于目标间权重系数难以平衡,基于Pareto的方法是当前多目标优化研究的主流。
Li等[51]提出一种基于博弈论的方法来研究多目标IPPS问题,并利用基于博弈论方法中的纳什均衡来解决多目标问题。Mohammadi等[52]充分利用勘探搜索和快速收敛的能力,提出一种多目标混合模拟退火算法 (multiobjective simulated annealing algorithm,MOHSA)。Mohapatra等[53]将IPPS视为可重构制造环境下的多目标优化问题,采用非支配排序GA二代(non-dominated sorting GA-II,NSGA-II) 处理问题的计算复杂性。Li等[54]用多层结构改进了解的表示,并应用NSGA-II来解决多目标IPPS问题。Jin等[55]提出一种多目标Memetic算法来解决多目标IPPS问题。Shokouhi等[56]将最小化最大完工时间、最小化关键机器负荷和最小化机器总负荷作为目标函数,尝试以加权的形式应用GA求解多目标IPPS问题。Zhao等[57]提出一种基于两代Pareto的ACO算法,求解具有可选工艺路线和不相关并行机器的多目标JSP。Zhang等[58]以节能减排为目标,利用工艺规划与调度的集成,采用基于非支配排序的层级式多策略GA实现节能优化。
4 分布式IPPS问题的研究现状
在经济全球化的背景下,订单个性化的需求增加,导致了产品多样化的生产需求,制造企业正朝着大规模定制的方向发展。传统的制造和管理模式越来越难以满足现代企业的发展要求。因此,制造模式开始从传统的单一车间向分布式多车间演变。分布式制造已逐渐成为一种重要的趋势,并已在许多重要行业有了成功的应用,如航空、航天、电子制造等。2021年的Science最新发文也指出了分布式制造的重要性[59]。
分布式车间调度的研究专注于分布式制造系统,在企业、工厂和车间之间分配工作计划,为各企业、工厂或车间生成生产计划,以优化生产指标。根据不同工厂的具体情况制定生产方案至关重要。通过合理分配工厂间的生产任务,管理者可以更好地处理单一生产的风险,降低相应的生产成本和产品交付周期。
分布式制造模式已经成为工业中的一个典型现象。目前关于分布式制造的研究主要集中在分布式流水车间或分布式作业车间问题上,其中工厂的结构大多被看作是同构的。但实际上,不同工厂的生产能力不同,对于相同的零件,各工厂可以提供完全不同的可选工艺方案。将每个工厂视为一个简单的同构作业车间环境,是对柔性制造能力的忽视和浪费。因此,考虑分布式制造中的异构工艺柔性,即分布式IPPS (distributed IPPS,DIPPS) 问题,更适合于实际生产环境。与分布式JSP (distributed JSP,DJSP) 或分布式FJSP (distributed FJSP,DFJSP) 相比,DIPPS问题更贴近实际生产需求,同时更有研究价值。
Wu等[60]首次将分布式虚拟制造 (distributed virtual manufacturing,DVM) 环境中的工艺规划问题和车间调度问题同时考虑,还基于Java的多代理系统(multi-agent system,MAS) 实现了DVM中的集成框架。最后,通过在仿真环境中建立虚拟制造模型,并与实际生产中的顺序制造方法进行对比,验证该方法的有效性。在综述文章中,Shen等[40]分别讨论了分布式制造系统中工艺规划问题和车间调度问题的研究现状,并介绍了基于Agent方法在解决分布式工艺规划和调度问题方面几个潜在的优势,为后继研究者们在DMS (distributed manufacturing system)中同时考虑这两个问题,提供了开创性的想法。Wang等[61]对DMS中工艺规划和车间调度的研究进行了系统的综述,讨论了当前的生产模式以及现有优化方法的局限性。Zhang等[62]研究了DMS中的工艺规划与调度问题,提出一种多目标GA来解决该问题。上述研究虽然在同一个DMS中同时考虑了工艺规划和调度,但对于二者集成性的讨论还有待深入。随着对IPPS问题研究的深入,Zhang等[63]试图利用两类GA来解决DMS中的IPPS问题,即DIPPS问题。随后,研究对另一种扩展型的GA进行改进,用来解决模糊工艺规划与调度问题的分布式集成问题,该问题可视为DIPPS问题的变体类型[63]。Lin等[64]同样是基于GA框架,通过生成负载均衡解来更有效地搜索DIPPS问题解空间,并比较3种类型染色体表示的优劣。
5 研究现状总结与问题分析
虽然IPPS的研究已经取得较好进展,但依然不完善,还有很大的探索空间。
1) 当前工艺规划问题以及IPPS问题的模型在求解大规模案例时,求解效率低下,无法在短时间内获得最优解。
2) 工艺规划和车间调度的集成方式一直是IPPS问题的研究重点。现有IPPS研究中的集成方式还有待改进,子系统间的结合还不够紧密,无法充分发挥工艺规划与车间调度的互补属性。
3) 现有多目标求解方法较少考虑子系统的耦合关系,决策者常常难以把握各优化目标间的权重,对多目标决策造成困扰。
4) 在分布式制造系统中,求解IPPS问题时考虑分布式制造的特征还不充足,无法充分发挥分布式制造的优势。
针对上述现状,IPPS未来工作可聚焦在以下几点。
1) 对问题模型进行线性化研究,建立可高效求解的MILP模型。此外,研究更为通用化的建模技术,为实际生产中的约束与优化目标处理提供技术基础。
2) 进一步研究更有效的集成方式,充分释放二者的柔性,拓展制造系统整体的优化空间。其主要方向可以为研究求解算法的个体编码表达,以及数学模型层次间的耦合关系构建。
3) 多目标优化可存在于IPPS问题研究中的不同层面,协调工艺规划子系统与车间调度子系统不同目标间的优化,以达到制造系统多目标的整体优化,是未来重要研究方向之一。
4) 考虑各分布式工厂的异构工艺及生产条件,探索更符合分布式系统的特征的DIPPS求解方法,是促进未来分布式制造系统发展的重要手段。
