轮轨磨耗对车辆系统动力学性能的影响

2022-07-15崔锦涛杨湘平

机械工程师 2022年7期

崔锦涛，杨湘平

（昆明铁道职业技术学院机车车辆学院，昆明 650208）

0 引言

近年来随着我国铁路行业的迅速发展，涉及铁路运营过程中的安全性、经济性问题日益突出[1-3]。尤其是轮轨磨耗问题受到广泛的关注研究，该问题作为轮轨关系中的一个普遍问题。研究掌握轮轨磨耗的特征规律对于我国铁路事业的发展和运营具有重大的理论和实际意义。车轮踏面磨耗是车辆运用过程中不可避免的一类现象，轮对的磨耗直接影响轮轨接触关系、运行平稳性及安全性。目前，随着轮轨磨耗程度的不断加剧，车辆运行中的振动加速度也随之增大，横向稳定性及平稳性随之下降[4]。轮轨磨耗对车辆的动力学性能有很大的影响。因此，研究车辆在不同磨耗下的动力学性能，对验证轮轨接磨耗预测模型的准确性和保证列车运行安全可靠有重要意义。

1 动力学模型

车辆系统动力学模型属于多刚体动力学理论，其系统组成部件及相互作用力繁多，由此产生的动力学行为更是存在较多的非线性因素。如何处理各部件之间的相互作用力和相对运动关系是建立动力学模型的基础。车辆系统动力学建模主流方法是将垂向系统和横向系统分别建模，根据轮轨接触关系将横向和垂向系统进行空间耦合处理，而轮轨接触关系模型也存在多种轮轨接触理论，针对本文所研究的内容，在建模过程中将起重要作用的因素表现出来[5]。本文将车辆系统视为多刚体系统，将悬挂系统视为等效线性刚度阻尼系统，其特性用数学模型来描述，通过锥形踏面和Hertz轮轨接触理论将车辆的垂向运动和横向运动耦合在一起。

1.1 车辆空间动力学模型

以CRH2型动车组为载体建立动力学模型。为了更接近实际情况，将车辆在横向和垂向平面内的运动耦合起来，建立图1所示的具有27自由度的车辆动力学分析模型。取车辆前进方向为X轴，水平向右为Y轴，与X轴和Y轴成右手坐标系的轴为Z轴。车体、转向架及轮对的各个自由度的运动正方向按右手定则选取，该系统的自由度如表1所示。

表1 自由度参数列表

图1 整车动力学模型

车辆系统空间动力学模型微分方程组可用矩阵形式表示为

1.2 Simulink模型

Simulink可以实现建模、仿真、动态分析的可视化仿真工具，以各种类型的子模块可以搭建出线性系统、非线性系统及数字信号处理系统。本文使用连续系统模块（Continuous）、数学运算模块（Math Operations）、信号源模块（Source）等建立车辆系统动力学模型。其基本思路是：利用过程信号连续时间积分模块（Integrator）建立出车辆每个部件的动力学微分方程；以输入输出模块定义方程中的每个变量，并建立该部件的微分方程组；将该微分方程组封装为一个子函数，以多个车辆系统部件子函数形式建立整车系统模型，所建立的子函数如图2所示。

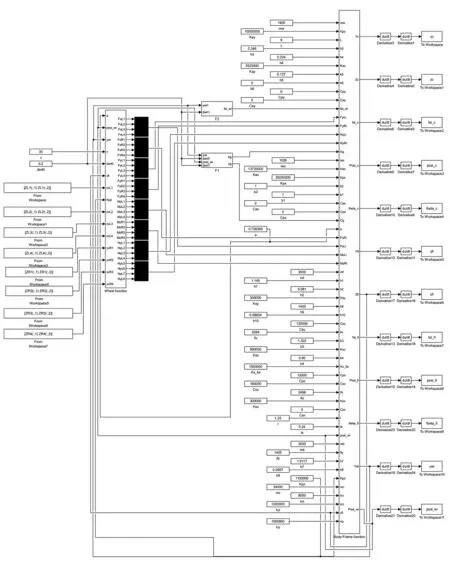
图2 Simulink动力学模型

2 轮轨接触模型

轮轨接触模型[7]主要有3个部分:1）接触几何关系，即计算轮对相对于轨道给定位置的接触点位置；2）轮轨接触（蠕变和自旋）的动力学特性计算；3）根据几何参数和运动参数计算接触处的轮轨力和蠕滑力。

这些问题不是独立解决的，一般需要通过迭代进行。本节所述的轮轨接触相互作用几何形状的主要计算方法是根据轮轨截面曲线（剖面图）的精确几何形状匹配进行的。为了提高接触点位置计算的可靠性和速度，实现了两个基本思想。首先，如果轮轨轮廓线沿着轨道运行方向是恒定不变的，在建模过程开始的时候，对轮轨轮廓线的接触点坐标进行一次计算。根据车轮轮廓相对于钢轨轮廓的位移，找出初始接触点坐标。假设车轮相对于钢轨有两个自由度：绕纵轴旋转（侧滚）和横向位移。在坐标计算过程中，轮轨接触点下一次迭代计算（初始迭代点为车轮轮廓相对于钢轨的当前位置）是通过上初始位置结算处的阵列矩阵进行插值计算得到的。这样的做法可以减少算术运算数量，提高运算速度。本节介绍了我国几种典型的车轮踏面类型，并分析了这几种不同类型踏面类型静态接触几何关系。

目前，我国高速铁路动车组主要采用3种不同踏面。其中，CRH1型CRH2型动车组采用LMA踏面，CRH3型动车组采用S1002CN踏面，CRH5型动车组采用XP55踏面[6]。这几种不同型号的踏面与60 kg/m静态接触几何关系如图3所示，其中：侧滚角为0°；轨道倾角为1：40；横向位移范围为-15～15 mm；轨距为1435 mm。

图3 几种踏面接触静态关系

根据轮轨磨耗预测模型仿真结果，结合现场运用数据，以动车组在一定运行里程后的磨耗踏面为研究对象，选取了轮轨磨耗预测结果中2种不同磨耗程度的踏面和标准60 kg/m匹配。其匹配关系如图4所示，其中磨耗踏面2的运营里程大于磨耗踏面1。

图4 磨耗踏面接触静态关系

3 动力学性能分析

以GB 5599—1985《铁道车辆动力学性能评定和试验鉴定规范》为标准，对车辆在不同踏面状态下的运行平稳性、临界速度及非线性特性进行对比分析。

3.1 横向稳定性分析

由于车轮踏面具有一定的锥度，当轮对沿着钢轨滚动时，会产生一种既沿横向运动又绕着轴质心的铅锤轴向转动的合成运动，当车辆运行速度达到一定值时，车辆的这种蛇行运动将会发生失稳。轮对一旦丧失稳定性，车辆各部件之间的作用力和振幅将明显增大，车辆动力学性能也将急剧恶化，同时还会造成轮轨间的严重磨耗，且增加了发生车轮脱轨的危险性。随着高速动车组运营速度的不断提高，改善轮对横向稳定性显得尤为重要，而轮轨磨耗对于车辆的横向稳定性影响也是需要考虑的一个重要因素。本节以两种不同磨耗程度的踏面为研究对象，分析了车辆在匹配不同踏面时的蛇形临界速度。

对标准轮轨和磨耗轮轨临界速度计算结果如图5所示。其中图5（a）、图5（b）分别为磨耗踏面1、2轮对横向位移随速度的不断增大的时间历程图，从图5（a）中可以看出随着车速的不断增大，轮对振动经由轮对平衡进入不稳定极限环最终进入稳定极限环的过程。其中磨耗踏面1不稳定极限环位于速度510 km/h附近。磨耗踏面2极限环位于475 km/h附近。从中可以看出车轮磨耗程度越大，其临界速度降低。图5（c）为匹配标准轮轨时，从中可以看出车辆的临界速度为535 km/h。

图5 不同踏面临界速度

3.2 非线性分析

考虑车轮和钢轨之间的横向间隙，当动车组高速运行时在轨道不平顺等外界激扰的作用下，轮轨在横向方向存在复杂的非线性行为。在分析轮对的蛇行运行时，由于存在轮轨间的黏着以及横向间隙使得轮对横向位移的响应会随机地绕系统的极限环摄动，极限环的表现形式可以反映轮对的周期运动特性。研究表明，蛇行运动存在Hopf分岔行为[7-9]，为进一步探究轮轨磨耗对动车组的蛇行运动影响，以标准轮对和磨耗轮对为研究对象，计算分析了动车组轮对的横向运动，如图6所示。

对于一个非线性的系统而言，通常其极限环将以混沌方式出现，从而引起系统周期响应的本质变化，非线性车辆系统的蛇行运动一般会出现3种主要的分岔形式：亚临界、吸引域超临界和单点超临界[10]。从图6中可以看出，随着踏面磨耗程度增加，其平衡位置趋于稳定。以此为依据可推断，随着磨耗的增加，蛇行运动分岔从吸引域超临界进入单点超临界，而本文中的系统是否经由亚临界分岔发展而来，还需进行深入的研究分析。

图6 磨耗轮对横向振动

3.3 运行平稳性

依据GB/T 5599-1985《铁道车辆动力学性能判定和试验鉴定规范》的规定，可以振动加速度作为车辆运行平稳性评价指标。以80、140、200、260、320、380 km/h的速度在直线线路上运行，对不同速度下的各项动力学指标进行计算分析。根据计算结果，在不同踏面状态下运行的动车组的平稳性指标达到了一级等级。随着踏面磨耗的加剧，横向加速度指标逐渐增大，但对垂向加速度的影响并不大，车辆系统运行加速度如图7所示，稳定性指标如图8所示。

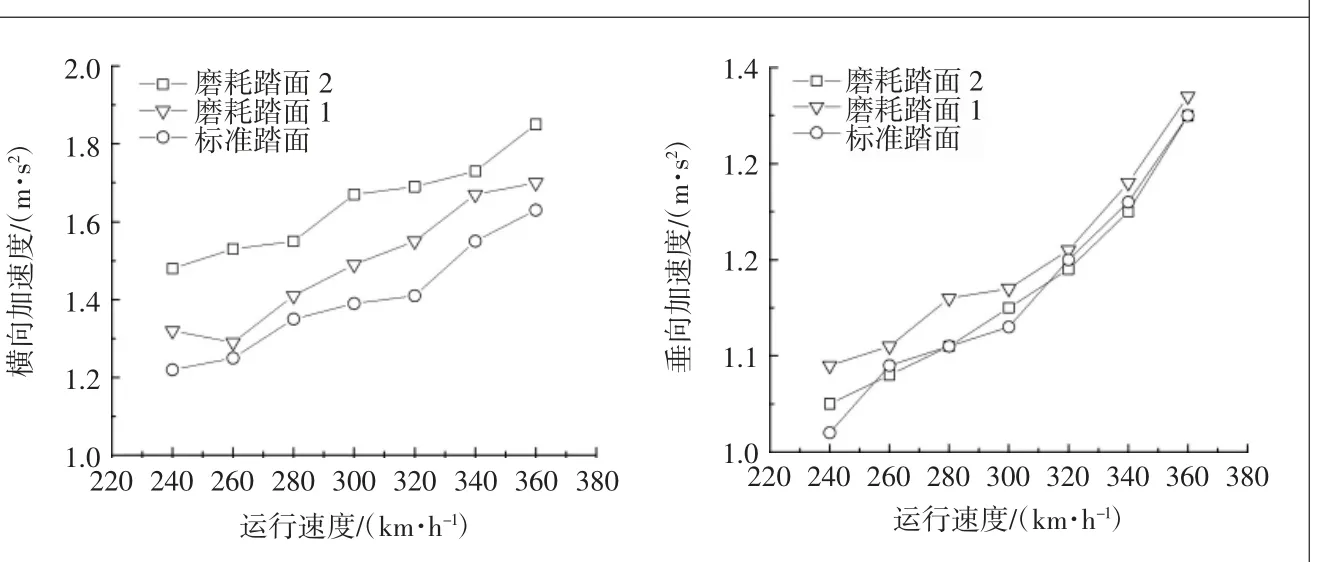
图7 车辆最大加速度

图8 车辆平稳性指标

根据平稳性指标计算结果，在两种磨耗程度不同的踏面状态下，动车组的平稳性指标均满足GB/T 5599-1985《铁道车辆动力学性能判定和试验鉴定规范》中一级等级要求。其动力学性能结果与加速度指标类似，踏面磨耗程度不断增大导致了踏面等效锥度增加，从而导致车体横向振动加剧；因其圆周磨耗较为均匀且未造成车轮圆度变化，因此对车体垂向振动影响不大。