基于启发式Q学习的汽车涂装车间作业排序优化

金 淳, 冷浕伶, 胡 畔

(大连理工大学 经济与管理学院,辽宁 大连 116024)

0 引言

汽车制造业是制造强国战略中推动智能制造发展的重点领域。目前，汽车制造业正在向高效化、个性化、灵活化方向发展以有效应对客户的个性化订单。在汽车制造流程中，涂装车间作业是连接车身车间、总装车间的中间环节，其涂装作业排序问题十分复杂，除了作业顺序要尽可能与总装作业计划顺序保持一致，还受到喷枪颜色切换条件的限制。喷枪每切换一次颜色都要使用特定溶剂进行清洗，如果频繁切换颜色，不仅会产生物料和时间上的浪费，而且会对设备造成一定损耗。因此，如何制定出可尽量减少颜色切换次数的涂装作业排序计划是涂装生产中面临的重要课题。

汽车涂装作业排序问题属于一类生产调度问题，该问题于2005年被法国运筹及决策支持学会列为制造业的挑战性问题之一[1]。目前国内外相关研究大多是构建问题的0-1整数规划模型，以颜色切换次数最少为目标，采用如遗传算法[2]、基于规则的启发式算法[3,4]、贪心算法[5,6]等启发式算法进行求解。此外，部分研究还考虑了其他因素进行建模求解，如：刘春晖等[7]提出了从涂装的下线顺序开始进行反向计算的倒推排序算法；Celso等人构建了具有三个不同权重目标的优化模型，并利用贪心算法第次求解[8]；Estellona等人考虑涂装输出顺序对总装作业的影响，构建整数规划模型，并提出了分别适合大规模问题和小规模问题的邻域搜索算法[9]。

生产调度问题是一类典型的NP-Hard问题，大多研究采用启发式算法，如蚁群算法、遗传算法等给出问题的满意解[10,11]。由于启发式算法的结构较为固定，导致算法的搜索性能受到一定的限制，因此，近年来人们开始尝试具有强大学习能力的机器学习算法。机器学习算法能够通过学习有效调节模型参数，其搜索性能往往比启发式算法更好[12,13]，其中的强化学习算法可有效解决序列决策问题，因此被认为是解决生产调度问题的一种有效方法。而启发式强化学习通过与启发式优化方法的结合，可以进一步提高强化学习算法解决实际问题的效果[14～17]，其中启发式Q学习结合了强化学习的前瞻能力与启发式因子的整体评估能力，相比于启发式算法，能有效避免初始解质量不佳对寻优效果的影响。尽管强化学习算法已开始应用于作业调度领域的研究，但目前为止，其在汽车涂装作业排序问题中的研究还很少见。

综上，本文针对汽车涂装车间作业排序优化问题，同时考虑颜色切换及总装需求，构建多目标整数规划模型，提出启发式算法与Q学习相结合的求解方法。本研究为解决涂装车间作业排序问题做出新的算法尝试，并试图为大数据时代基于数据驱动的涂装车间生产调度问题提供新的解决方案。

1 问题描述

涂装车间的涂装作业策略原理如图1所示。图中的圆圈表示待涂装的对象(白车身)，用圆圈的不同填充方式区分颜色，用不同字母区分车型。图例中，一个总装需求序列包括3种颜色、4种车型、共14个车身，排序前颜色切换共11次，经过排序后颜色切换共5次。一个涂装作业策略包括两部分，一是要涂装的颜色顺序，二是各颜色每次涂装的批量大小。当涂装某种颜色时，将一轮涂装的车身数量称为该颜色本轮的涂装批量，该轮涂装称为一个涂装轮次，则每种颜色的车身都会在整个涂装过程中被分为一个或多个涂装轮次，一种颜色各个轮次的涂装批量可以不同。完成涂装作业的车身称为漆车身，它被放入涂装车间与总装车间之间的缓冲区，由总装车间按其需求从缓冲区逐个提取。

本研究中的涂装车间作业排序问题是指：为涂装车间找到一个最优的作业序列，既可使涂装车间输出车身的顺序尽量与总装车间的需求顺序保持一致，同时又可使涂装作业过程中喷枪颜色的切换次数最少。本文涉及的参数符号及含义如表1所示。

表1 部分参数符号及含义

本研究假设如下：

假设1作业时间用单位时长度量，单位时长定义为一个车身的涂装作业时长。每个车身(各颜色、各车型)的涂装作业时间相同；

假设2各颜色的涂装批量相互独立，调整某一颜色的批量大小不影响其他颜色的涂装批量；

假设3一旦开始涂装一个批次，须将该批次全部涂装完毕才能开始下一批次，中途不可中断；

假设4本文仅考虑涂装车间与总装车间之间的缓冲区，涂装车间内部的缓冲区忽略不计。

2 模型的构建

2.1 目标函数指标的定义

本问题的目标函数包括两个子目标：总装需求延误比例和颜色切换比例。具体定义如下。

(1)总装需求延误比例

本文衡量两个序列差异的依据是总装需求被延误的程度。由于实际涂装序列与总装需求序列存在不一致，导致总装车间需要的某些车身被延迟，总装车间等待这些被延误车身的时长的总和，就是该涂装序列造成的总装需求延误程度。

定义变量γ和τ共同计算实际涂装序列与总装需求序列的差异。用序列变量Π表示一个涂装序列中各个车身是否发生延误，γi∈Π,i=1,2,…,M，表示第i个车身是否被延误；序列变量Λ表示一个涂装序列中各个车身的延误量，τi∈Λ,i=1,2,…,M，表示第i个车身的延误量。计算总装需求延误程度时，指定一个容忍度变量η，η>0，表示允许车身发生一定的延误，若某车身的延误量处于容忍度η内，则不计入整个序列的总装需求延误程度。

定义变量ψ对总装需求延误程度进行归一化处理，表示一个涂装序列的总装需求延误程度与其序列长度的比值，即总装需求延误比例，表示如下。

(1)

(2)颜色切换比例

定义序列变量Ω表示一个涂装序列的颜色切换次数，δi∈Ω,i=1,2,…,M-1，表示第i个车身与第i+1个车身的颜色是否相同，若两者颜色不同，δi记为1，否则记为0。同样，对颜色切换次数进行归一化处理，定义变量χ表示涂装序列的颜色切换比例，表示如下。

(2)

2.2 优化数学模型

minΓ=αψ+βχ

(3)

(4)

(5)

(6)

(7)

lmax≤L

(8)

1≤u,d≤K

(9)

1≤v,w≤Z

(10)

α+β=1，0≤α,β≤1

(11)

约束条件(4)表示排序前后车身总数不变，式(5)和(6)分别表示排序前后各个颜色和车型的车身总数不变，式(7)表示各颜色各涂装轮次的批量大小不能超过其对应的上限和下限，式(8)表示涂装序列在缓冲区中存放的最大车身数量不能超过缓冲区容量上限，式(9)和(10)分别表示车身的颜色和车型不能超出给定范围，式(11)表示两个权重参数值分别处于0～1之间，且其和为1。

3 算法设计

本文提出一种针对涂装车间作业优化排序问题的启发式Q学习算法。由于本文算法是在Q学习算法上的改进，为此先介绍本文的Q学习算法设计。

3.1 Q学习算法设计

Q学习算法是一种离线策略时序差分强化学习(Temporal-Difference Reinforcement Learning)算法，它直接优化一个可迭代计算的状态-行为对价值函数，即Q函数，只要使用训练好的Q函数，就能得到最佳的动作序列[18,19]。设计Q学习算法时，一般要将问题表述为马尔可夫过程或半马尔可夫过程，并根据实际问题定义状态特征、动作及回报函数，以及算法的迭代方式[20,21]。本研究将涂装作业排序问题抽象为一个马尔可夫过程，认为作业排序过程是一种序列决策过程，如图2所示。则使用Q学习求解的基本思路是：使强化学习agent根据当前已涂装情况，预测接下来涂装哪种颜色和车型的车身能使收益最大化。

sw=(tc,hn,ro,cv,bt,lt,pv)

(12)

本问题的初始状态定义为：

(13)

本问题中，动作被定义为选择某一种颜色和车型的车身作为下一个要涂装的车身。具体如下:

(14)

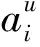
(15)

(16)

采取动作ac获得的即时奖励值re由四部分组成，说明如下：

(1)动作ac执行后造成的总装需求延误量，用变量ψs表示，ψs=γi·τi，i=1,2,…,M；

(2)动作ac执行后颜色切换次数是否增加，用变量χs表示，若增加，将χs置为1，否则为0；

(3)惩罚项ω，反映当前已占用的缓冲区大小l是否大于L，若大于，将ω置为某个正数Dp，Dp的值反映了惩罚力度的大小，否则将ω置为0。

(17)

(4)动作ac执行后，该车身是否需要在缓冲区停留，用变量φ表示，若需要，将φ置为1，否则为0。为使缓冲区得到充分利用，车身需要停留时，给一个较小的奖励wb，wb>0，与惩罚项ω配合能使缓冲区的占用量处于合理范围内。

由于Q值将收敛于最大值，因此re定义如下：

re=-(αψs+βχs+ω)+wbφ

(18)

算法主要流程如下(用不同的缩进值来体现算法的循环结构)：

Step1设置L，Dp，wb等算法参数；

Step2初始化Q矩阵为零矩阵；

Step3对于每一个世代(episode)：

Step4以初始状态sw0开始；

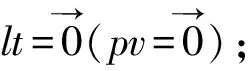
Step6在当前状态St下，在所有可能的动作中，选择一个可能的动作ac；

Step7执行ac，到达下一个状态St+1；

Step8对下一个状态St+1，基于其所有可能的动作，获得最大Q值；

Step9用Q函数更新公式计算状态-动作对St与ac对应的Q值，更新Q矩阵；

Step10设置下一个状态St+1替换为新的St，更新sw，返回Step 5；

Step11重复Step 3直至Q矩阵收敛或达到最大迭代次数。

训练结束后，就可以利用Q矩阵得到最优的涂装作业策略，即最优的涂装颜色和车型序列。

3.2 启发式Q学习算法设计

在大规模或复杂问题的求解中，强化学习算法会遭遇“维度爆炸”难题。对此难题，在算法设计时，一方面可从状态空间入手，用降维的方法降低状态空间的复杂度[14,15]；另一方面可通过给强化学习模型注入先验知识的方式，起到加快收敛速度和一定的降维作用，主要采用两种途径：一是使用启发式强化学习模型，使启发式函数与值函数一起作为奖励函数，共同指导训练[16]，二是利用强化学习帮助启发式算法提升搜索性能，避免陷入局部最优[17]。本文提出的启发式Q学习算法是基于第一种途径，在Q函数中引入启发式因子，可在一定程度上引导Q学习的搜索方向，具有更好的实用价值。

本文在传统Q学习算法方案的基础上，加入了遗传算法中适应度的概念。在更新Q函数时，不仅考虑动作ac带来的期望奖励，同时在整体上评估已涂装序列的适应度，共同引导Q学习的搜索方向，以加快搜索效率。

定义启发式Q学习中的适应度函数为：

(19)

该适应度函数由四部分组成，设当前已涂装序列的长度为M′:

(1)已涂装序列的总装需求延误比例ψh，即

(20)

(2)已涂装序列发生的颜色切换比例χh，即

(21)

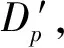
(22)

因此在启发式Q学习算法方案中，Q函数的更新公式为:

Q(St,At)←Q(St,At)+σ(Rt+1+υQ(St+1,A′-

(23)

其中，σ和υ分别表示Q学习算法中的学习率和衰减系数，ρ表示启发式因子的权重，ρ越大表示启发式因子的影响力越大。

4 数值实验及分析

4.1 实验设计

本研究在企业调研实际数据基础上生成两个算例，分别包含650个和1300个涂装作业，包含6个车型和10种颜色。部分作业详情如表2所示。

表2 部分车身详情

本实验将本研究提出的启发式Q学习算法与遗传算法、传统Q学习算法方案进行对比，以证明本研究算法的有效性。求解算法采用Java和Python编写，实验环境配置如下：Intel i7-7700处理器(3.60GHZ)，8G内存，Windows 10操作系统。

4.2 实验结果

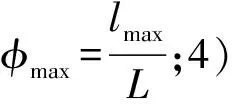
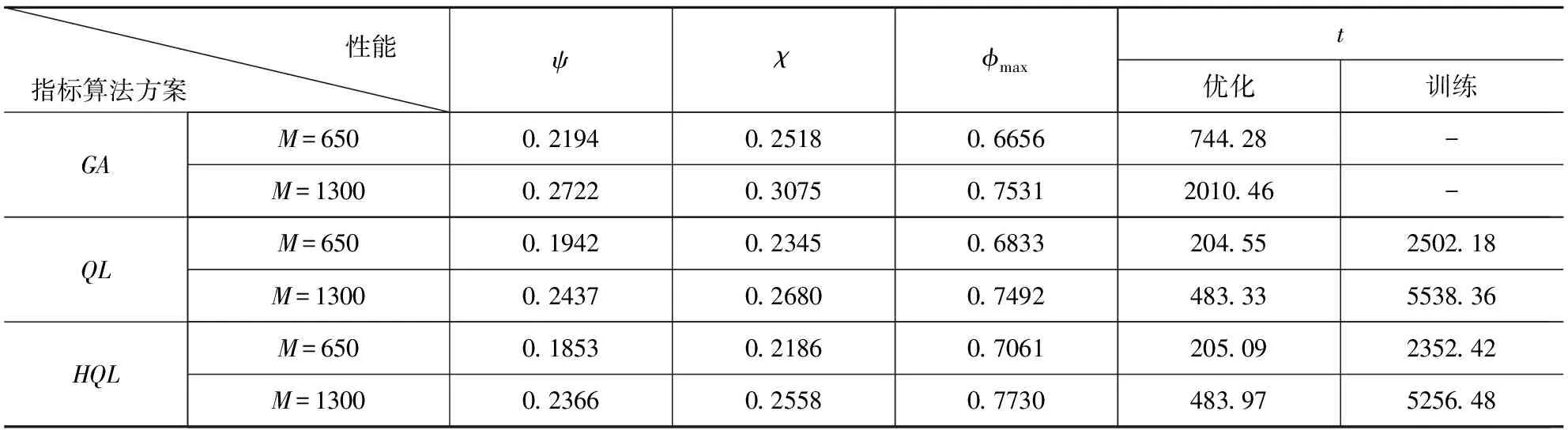
表3 平均计算结果

如表3所示，QL和HQL的运行时间分为两个部分，首先通过一段时间的训练得到Q函数，再使用Q函数得到优化结果。从表中结果可知：QL和HQL比GA表现更优，HQL比QL表现更优。在M=650算例上，本文算法得到的ψ比GA低15.54%，比QL低4.58%，得到的χ比GA低13.19%，比QL低6.78%。在M=1300算例上，本文算法得到的ψ比GA低13.08%，比QL低2.91%，得到的χ比GA低16.81%，比QL低4.55%。

4.3 结果分析

(1)缓冲区容量L对涂装作业排序结果的影响

表4给出了本文算法在L分别取25、50、100、150时的各个指标值，其中设置α=β=0.5，η=20。图3～5给出了三个指标随着L变化的曲线。从以上结果可得，L与上述三个指标在一定范围内呈反比关系，适当地增大L能提高解的质量。过小的L成为瓶颈因素，限制了算法的寻优能力；当L过大，L足够满足需要，此时解的质量取决于算法本身的寻优能力。实际应用中可以根据曲线的拐点确定最优L值。

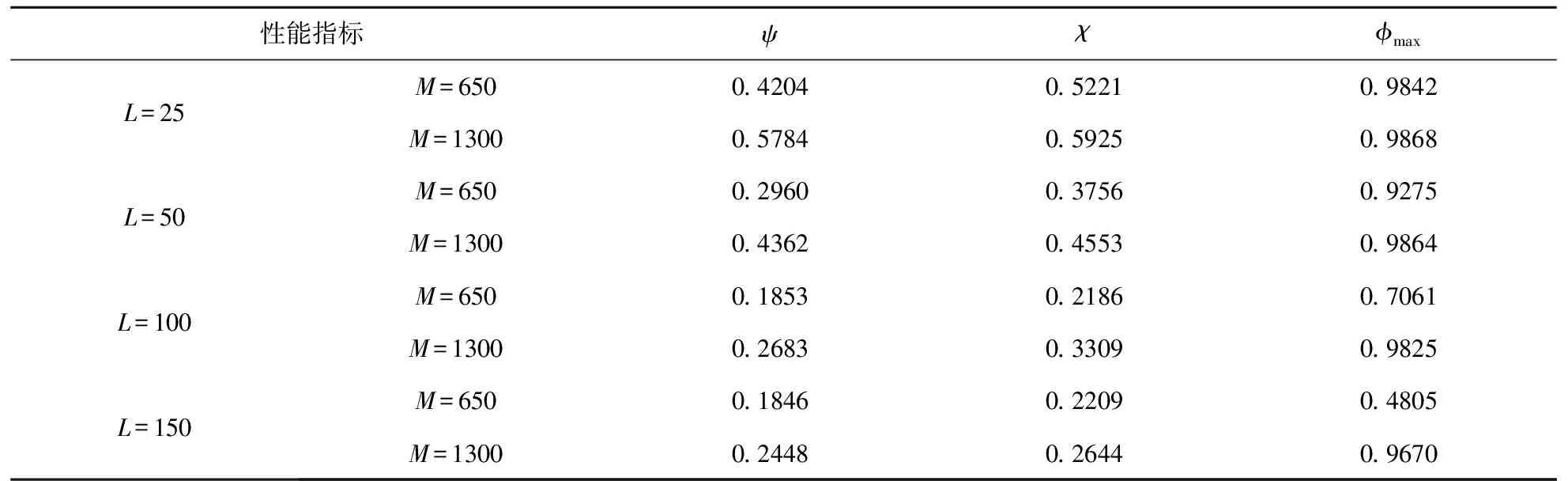
表4 L对涂装作业排序结果的影响

(2)容忍度变量η对涂装作业排序结果的影响

表5给出了本文算法在η分别取10、30、50、70时的各个指标值，设α=β=0.5，L=200。图6～8给出了三个指标随着η变化的曲线。从以上结果可知，随着η的上升，一方面ψ有较大幅度的减少，另一方面由于对延误情况的惩罚力度降低，agent在训练过程中对延误情况不敏感，因此会为了进一步降低χ而增加对缓冲区的利用。然而当η增加到一定程度时，由于算法本身寻优能力的限制，χ和φmax都会趋于稳定。

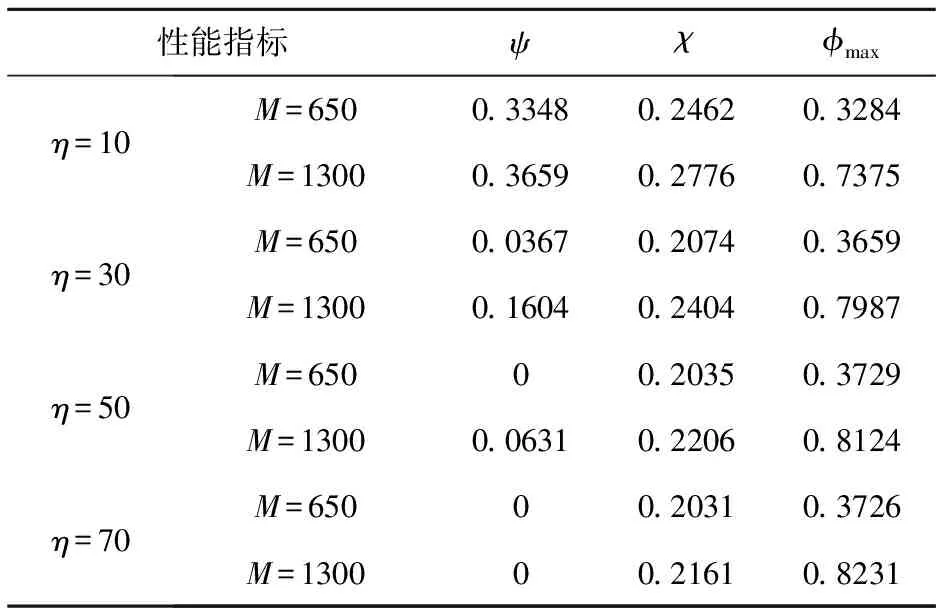
表5 η对涂装作业排序结果的影响

(3)权重α、β对涂装作业排序结果的影响

图9～11给出了本文算法在M=650，L=100且两个权重变量满足α+β=1时，ψ、χ、φmax的变化曲线。由结果可得，α和β的关系为算法搜索起到了导向作用，当α=1，β=0，算法只有一个优化目标，ψ会尽可能降至最低，而χ则被忽略，反之亦然。

(4)算法方案对比

由以上实验结果可得，本文算法比传统Q学习算法表现更优，强化学习算法方案比遗传算法方案表现更优。强化学习算法方案训练时间长，得到的解更优，问题规模越大启发式因子对解的质量和搜索效率的提升作用越明显。

5 结论

本文针对涂装车间作业排序优化问题开展研究，结论如下：

(1)构建了以降低总装需求延误和颜色切换次数为目标的多目标整数规划模型。将问题抽象为马尔可夫过程，提出了基于启发式Q学习算法的解决方案。

(2)通过对本文算法、遗传算法、Q学习算法的比较实验结果表明：强化学习算法方案比遗传算法方案表现更优，本文算法比传统Q学习算法表现更优。本文算法能够有效求解汽车涂装车间作业优化排序问题，其优势在于：结合强化学习算法的前瞻能力与启发式因子的整体评估能力，相比遗传算法能降低对初始解质量的依赖。

(3)本算法的特点在于：在训练阶段，如果数据充分，虽然训练时间更长，但算法训练效果更好，可以得到更优的解；问题规模越大启发式因子对解的质量和搜索效率的提升作用越明显；在优化阶段，可以用比遗传算法更短的时间得到更好的求解结果。其意义在于：在大数据和智能制造时代，利用高性能计算资源和海量数据，采用线下充分训练，线上快速求解的方式实现比启发式算法方案更为满意的优化结果。

今后的研究可以继续深入考虑以下两个问题：一是建模中考虑作业过程可能出现的返修情况；二是尝试将强化学习算法与其他优化方法相结合，以进一步提升求解质量和搜索效率。