基于多目标进化聚类的信用风险特征识别

刘 超, 李元睿, 谢 菁

(1.北京工业大学 经济与管理学院,北京 100124; 2.北京现代制造业发展研究基地,北京 100124)

0 引言

当今世界的金融市场呈现出电子化、全球化和虚拟化的特点，逐渐走向数量化和信息化时代[1]。具有无实体性、高效性、风险性和难量化特征的金融大数据逐渐涌现。但这些数据并没有被有效利用，造成了“数据资源充足但产出不足”的现象。这一现象引发了对海量金融数据的数据挖掘需求，从而进一步将数据资源转化为高附加值信息资源[2]。

信用风险是一种具有较大危害且易于大范围传播的金融风险,泛指由于信用资产质量降低而直接引发金融资产损失严重的一种可能性[3]。与金融信用风险相关的数据往往呈现出高维度、大规模和不对称等特点[4]。其中，数据的高维度特点是在数据挖掘中最突出的问题[5]。因此针对具有高维度特征的信用风险数据，设计适用于此类数据的数据挖掘技术，对处理金融信用风险相关问题具有重要意义。

聚类是一种不需要数据标签，便能深入挖掘数据内部结构特征的数据挖掘技术，在上市公司的信用风险评价问题中具有广泛的应用[6]。但在具体实践中，传统的聚类算法在处理具有高维特征的信用风险问题时暴露出两方面不足：①大量冗余特征导致类簇可能分布在高维空间的某一个特征子空间内。②稀疏的高维空间使得样本的相似度难以衡量[7]。因此，如果将每个特征维度的权重视为均等的，那么所得到的数据的相似度将不再准确。利用低维特征子空间表征高维数据已被证明是一种降低高维数据复杂性的可行方法[8]。目前此类研究已形成了一系列经典子空间聚类算法[9～11]。然而，现有算法尚存在一些缺点，如：①目标函数不足以支持特征子空间的搜索；②使用贪心策略进行搜索，易陷入局部最优[12]。使用进化算法能够在上述问题中有效改进子空间聚类。同时，采用多种聚类目标函数能够使结果更具有丰富的意义，增强了对不同应用场景的鲁棒性[13]。

1 问题描述

1.1 子空间与特征识别

在具有高维特征的信用风险数据聚类过程中，可能存在以下难点[14]：①从全局特征来来看，样本中可能混杂噪声和冗余的特征；②从局部特征来看，类簇的特征可能由不同的一组属性表示。传统方法通常采用全局性的视角，对数据进行统一的降维处理，但无法体现和区分样本之间的局部特征差异[15]。子空间聚类算法与采用全局视角的传统聚类方法有明显差异。为了体现研究数据在全局和局部的特征，引入权重向量，对不同数据维度赋权。同时，在目标函数中采用加权距离，可增强类内样本的相似度和类间样本的差异度。

1.2 子空间聚类目标函数

子空间聚类将数据划分建模为一类优化问题，其优化模型可以概括为[16]：

(1)

式中，变量U代表每个样本点被分配给各个类簇中心的隶属度，变量V是类簇中心的坐标，变量W代表体现类簇特征的权重。该模型包含N个维度为D的样本，通过优化该模型，将样本划分为C个类。样本与类簇中心的距离由d(vik,xjk)表示。H(U,W)表示额外添加项，各类子空间聚类算法的变种主要根据该项的变化以得到不同聚类效果。总体上，子空间聚类算法的主要思想是在将特征权重作为优化变量之一，同时优化聚类中心的位置，使分配到同一类的样本与聚类中心的相似度最小，从而完成对样本的划分。

2 算法提出

2.1 目标函数

传统的子空间聚类算法使用加权求和的途径将各个评价准则统一至单一目标函数中，从而追求各准则之间的折衷[17]。本文同时考虑多个聚类准则，其中包括：同类样本间的紧凑性，不同类样本间的分散性和特征权重的负熵。构建子空间聚类的三目标优化模型：

(2)

其中，f1表示样本与类簇中心的差异。最小化f1将使得聚类结果中，差异小的样本被划分为同一类。f2衡量类间分离性。f3通过对特征权重负熵的最小化，来避免特征权重分配时的极端不平衡状况。

2.2 算法流程

使用基于分解的方法求解公式(2)中的子空间聚类三目标优化问题。设计基于分解的多目标子空间聚类算法(Decomposition-based Multi-Objective Subspace Clustering, DMOSC)。整体流程如算法1所示。首先对数据进行标准化，并随机初始化种群(算法1步骤3，4)。之后，使用交叉、变异算子对个体产生扰动，使其产生新解[18,19](算法1步骤7)。并进行局部搜索，提高算法效率(算法1步骤8)。在扩大的种群中采用精英选择机制，将优秀个体选择进下一次迭代。达到停止条件后，得到样本的聚类划分结果。

算法1 DMOSC算法整体流程

2.3 染色体编码

DMOSC使用基于原型的染色体编码[20]。类簇中心作为该编码方式的基本基因片段，使染色体长度不随样本规模扩大而提高[21]。如图1所示，染色体中包含所有类簇中心的坐标，即矩阵V的每一行向量，根据染色体信息可以计算得到聚类变量U,W。

图1 DMOSC染色体编码

2.4 局部搜索

为提高算法性能，本文借鉴MOEA/D[22]算法的分解思想，将整个目标空间进行分解，得到若干个互不相交的区域，在每个分解后的空间内进行目标函数的标量化处理，从而实现局部搜索。具体步骤如算法2。

算法2 DMOSC局部搜索

具体来讲，首先生成若干个子目标空间，使这些子目标空间是目标空间的均匀划分。然后将每个个体分配给不同的子目标空间，该步骤通过衡量个体与参考向量的距离完成(算法2步骤1,2)。图2展示了第n个子目标空间的局部搜索：阴影区域表示子目标空间，使用该空间内参考向量的坐标(αn,βn,γn)作为目标函数权重，生成如公式(3)所示的各局部搜索空间的标量化目标函数。

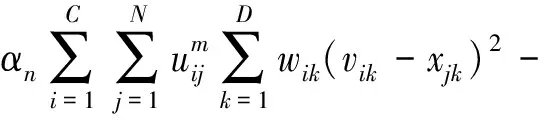
(3)

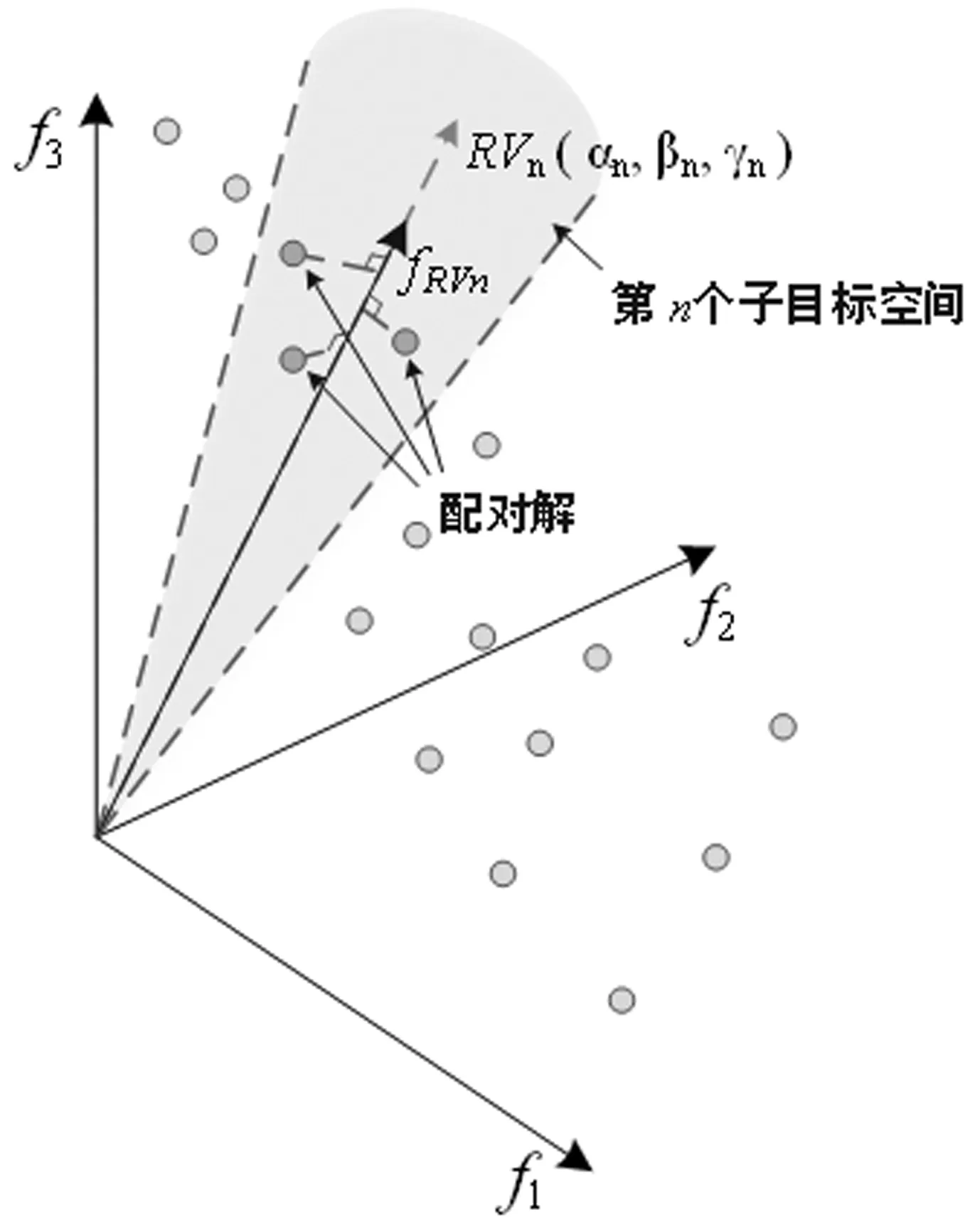
图2 局部搜索标量化目标函数

局部搜索的实现途径是对该局部标量化目标函数的迭代优化(算法2步骤5～7)。各聚类变量的更新公式由定理1，定理2和定理3给出。

定理1对公式(3)所示的优化问题，若给定V和W，且有m>1，则U的局部最优解为:

(4)

定理2对公式(3)所示的优化问题，若给定U和W，且有m>1，则V的局部最优解为:

(5)

定理3对公式(3)所示的优化问题，若给定U和V，且有m>1，则W的局部最优解为:

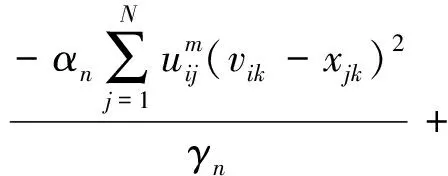
(6)

3 实证分析

3.1 样本选取

本文选取上市公司为样本，最终评价聚类结果的判定标准是对比证券交易所执行的特别处理机制(Special Treamtment，ST)。即，收集带有标签的两类数据，分别代表具有高、低风险的样本。样本标签仅用于对聚类结果的评价，依据是否被执行ST来确定，ST机制使用评价年份之前两年的财务数据，对财务困境进行识别和分析。

收集的数据来源为2017年度，其中，共有48家A股上市公司被执行ST。将这些公司纳入本研究中的高信用风险样本。为保证公平性，低风险样本的选取规则为：对每个高风险样本，选取两个近似行业和经营规模的未被执行ST的样本。则本研究的总样本个数为144，两类数据样本数量的比例为1:2。这些样本在2017年是否被实施ST是根据前两年的经营情况进行评判的。根据与信用风险相关的财务数据构建指标体系，然后将2015年度和2016年度的数据收集整理，作为DMOSC算法的输入，以此来识别并区分不同风险等级的样本，并与真实标签进行比较。

3.2 信用风险指标体系

测度信用风险需要使用合理的信用风险指标数据，是其能够全面地反映信用风险，并具备一定的层级性[23]。本研究将基本财务因素、现金流量因素和长期发展潜能因素三部分作为评价信用风险的主要宏观因素。根据这些因素进一步设立描述这些影响因素的能力体现。在每类能力体现下，分别继续进行细分，设立体现信用风险因素的具体指标。如表1所示。

表1 信用风险指标体系

3.3 信用风险评价实验描述

根据所建立的信用风险指标体系收集实验数据。数据来源为万得(Wind)数据库。并对样本分配标签，作为评价算法结果的标杆。样本标签来源为2017年证监会公布的风险警示名单。运用其前两年的公司运营数据判断本年度上市公司股票是否被归为ST股。但各指标在每个年度的重要程度并不一定是一致的，因此，对各个年度分别进行研究，即数据集D1表示第一年度的数据，数据集D2表示第二年度的数据，数据集D3表示两个年度的数据。

在所有数据集上应用DMOSC算法进行实验。并使用全空间聚类算法和其他子空间聚类算法变种进行对比，包括：FCM[24]，K-means[25]，EWKM[16]，ESSC[8]，MOEASSC[26]。最终结果的准确性通过将各算法的结果与实际是否被实施ST进行对比得到。使用RI指数[27]、NMI指数[28]和Kappa指数[29]衡量聚类结果的准确度。在取值范围上，RI与NMI指标是介于0和1之间的实数，Kappa理论上在[-1,1]上取值，但在实际应用场景中通常落在[0,1]内。在这些指标的评价方面，数值越大越符合实际，即表示更加精确的聚类结果。

实验参数设置如表2所示。DMOSC以及其他对比算法分别在D1，D2和D3数据集上进行聚类，为避免算法随机性的干扰，每组测试运行20次，记录每次运行得到的聚类结果，计算聚类结果与真实标签的差异，采用指标的均值和标准差作为每组测试的评价结果。

表2 实验参数设置

3.4 聚类结果分析

在三个数据集上的聚类结果由表3，表4和表5展示，包括了三种聚类评价指数，横向对比中，加粗展示最优结果。如在D1数据集中，DMOSC的RI指标表现最好，则加粗强调该结果。

表3 D1数据集聚类结果

表4 D2数据集聚类结果

表5 D3数据集聚类结果

由表3所示的D1数据集的表现可以看出，在Kappa指数和RI指数上，DMOSC得到了最高的数值。而在NMI指数上，虽然ESSC算法取得最好结果，但DMOSC与其差距非常微小。从鲁棒性方面来看，经典聚类算法如K-means和FCM所得到的结果具有较小的标准差，领先于其他以子空间聚类为基础的变种算法。例如基于单目标优化的EWKM算法，其在RI指数和NMI指数上得到相对较不稳定的结果，且在Kappa指标上的聚类准确度明显劣于其他算法，这是由于该算法的目标函数缺少类间分离性的平衡，因此容易将大量样本归入同一类。而RI指标和NMI指标对不平衡数据的评价存在偏差，但被Kappa指标捕捉到这一现象。由表4所示的D2数据集的表现可以看出，DMOSC在RI，NMI以及Kappa等指标上都得到了最好的结果。从标准差所反映的结果稳定性方面，经典的全空间聚类算法优势明显，但在子空间聚类的各类变种中，DMOSC具有最好的鲁棒性。由表5可以看出，DMOSC以及其他对比算法在D3数据集的表现均比其他数据集上更优，并且DMOSC，EWKM和K-means在每次运行中均得到了于实际情况完全一致的划分。

对不同数据集进行纵向对比，可以看到，数据集的差异也是导致聚类结果精度的原因之一。总体来看，D3数据集上的结果最好，且与真实情况十分接近，D2数据集次之，D1数据集最差。这说明D3能够提供充足且有效的信息，以得到正确的划分。这与证监会评判上市公司是否被实施ST的准则相符，即综合考虑最近两年的财务数据。而在两年度的数据中，第二年度的财务数据(数据集D2)比第一年度的财务数据(数据集D1)更具有参考意义。

3.5 信用风险特征分析

DMOSC在聚类时对每个财务指标进行赋权，并在算法运行中自适应调整权重，以获得类簇内最小的加权距离。且在两类数据中，各财务指标的权重分布不同。权重的大小体现了不同指标的重要程度，进一步通过权重可以识别出反映信用风险的相对重要的财务指标。在D3数据集上，DMOSC对两年度的各财务指标的最终权重如表6所示。

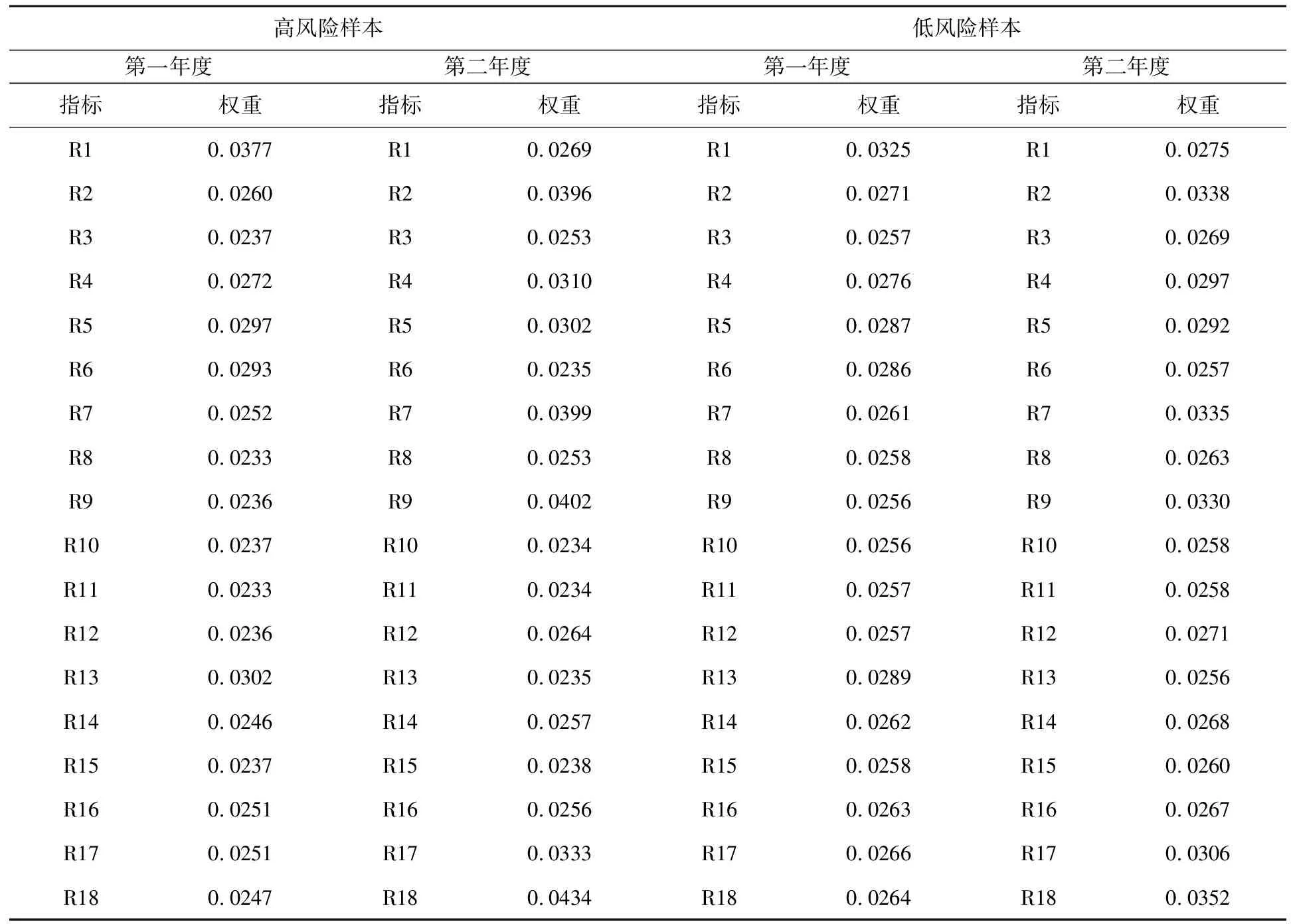
表6 两类样本信用风险指标特征权重

表6所展示的特征权重中，高信用风险样本和低信用风险样本所呈现的特征是不完全相同的。

高风险样本的指标权重特征在不同年份的差异明显，普遍地，第二年度的指标较第一年度指标具有更高的权重。具体来看，指标R1和R13在2015年的权重较高；指标R2、R4、R5、R7、R9、R17和R18在第二年的权重较高，其中，最显著的是R2、R7、R9和R18。因此，第二年度的诸多指标在信用风险评价中较第一年度相应指标具有更高的参考价值，其中体现盈利能力的包括R2，R4和R5，体现偿债能力的包括R7和R9，体现成长能力的包括R17和R18，体现出这些指标在评价信用风险时的重要性。第一年度的相对重要指标中，体现盈利能力的包括一个指标，体现现金流的包括一个指标。

低风险样本中，不同财务指标的权重差异性相对较小。但在第二年度，仍然能够凸显出一些重要指标，如R2、R7、R9、R17和R18等；第一年度中，只突显出单一重要指标R1。因此，第二年度的一些信用风险评价指标更具能够区分两类样本，包括偿债能力的相关指标、盈利能力的相关指标以及成长能力的相关指标。而在第一年度，盈利能力也具有一定的参考意义。

4 结论

信用风险评价需要从多个维度进行，每个维度又可能包含了若干不同的指标，因此具有数据维度高的特点。而其中某些指标并不一定起到关键作用，这使得风险特征往往存在于整个特征空间的某个子空间中。因此本文同时考虑加权的类间分离项、加权的类内紧凑项和权重向量的负熵以建立多目标优化模型。在求解阶段，使用基于分解的思想设计启发式算法以及局部搜索方法，并进行了评价上市公司信用风险的应用实验。分析两类样本的信用风险特征可得到如下启示：综合评价年度之前两个年度的数据进行判断，有助于信用风险样本的识别。在后续研究中，可将DMOSC算法拓展至信用风险时间序列的聚类问题研究，考虑时间维度对信用风险特征的影响，探究在动态环境下风险特征的演化规律。