Kapton薄膜高温单轴循环拉伸的力学性能

刘 岩, 刘俨震

(长安大学建筑工程学院,陕西 西安 710061)

为适应当前国防和航空事业的发展，完成我国各项深空探测任务，高精度大型空间可展开天线的需求越来越迫切.充气可展结构作为一种有前景的可折叠展开结构，代表着未来深空可展天线的发展方向之一[1-5].它在地面发射时为折叠收纳状态，收藏在整流罩内.待航天器进入空间轨道后，再由地面控制指令使其在空间轨道上按照设计要求逐步完成展开动作，最后锁定并保持为运营工作状态.

当天线沿空间轨道运行时，其相对太阳和地球的位置、方向不断变化(如图 1所示)，周期性地经受太阳直射和进入地球阴影区[6-7].具体表现为：在轨运行天线，从正照区(位置1)到阴影区(位置5)再回到正照区的过程中，其温度变化表现为先逐渐降低，再逐渐升高；进出阴影区时存在较大的温度突变，经历的高低温变化幅度可达-180 ℃～+180 ℃，属于极端温度作用.这样周期性的温度变化会使得反射面膜面应力呈变动状态，这必然会使得反射面膜材产生残余变形，致使膜面的预张力降低，影响膜材的使用.而对于充气可展膜结构而言，预张力是膜面成形并具备整体刚度的必要条件，预张力的损失会导致结构存在安全隐患，轻者会在膜面出现褶皱，重者会使膜面刚度失效而导致整体失效.研究Kapton膜材在循环荷载作用下的刚度及强度变化规律等，是确定膜材强度设计值、膜结构裁剪缩小率、张力调节装置等的重要前提.而Kapton薄膜是美国杜邦公司生产的一种具有明显黏弹性的高分子聚合物膜材，具有优良的化学稳定性、耐高温性、坚韧性、耐磨性、阻燃性、电绝缘性等.其诞生至今短短几十年，广泛应用于空间可展结构中.但与传统的建筑膜材相比，其膜材的力学性能研究仍相对落后.目前国内外对于膜材在循环应力作用下的研究多集中在建筑织物材料及飞艇蒙皮材料方面：罗仁安等[8]基于双轴试验，研究了PVC膜材的应力-应变关系、残余应变、滞回曲线；张营营等[9]对PTFE/GF和PVC/PES膜材的单轴拉伸破坏、循环加载变形及力学性能进行了研究；陈建稳等[10]对全新飞艇蒙皮膜材Uretek3216L进行了单轴循环拉伸试验，探讨了膜材本构关系及弹性模量随循环次数的变化规律；陈务军等[11]考察了ETFE及PTFE膜材的单轴反复加载性能，提出了相应的拟合公式.而关于Kapton膜材的研究较少，且研究主要围绕在Kapton膜材的化学制备、制作工艺等方面[12-14]，关于Kapton膜材的在不同温度工况下的力学性能研究较为缺乏，尤其是在循环应力作用下的力学性能尚未看到相关报道，无法判断其是否满足在航空航天领域中的应用.

图1 太阳照射的不同轨道位置Fig.1 Different orbit position during solar illumination

为了深入研究Kapton膜材的材料特性，进一步积累材料特性数据，本文对Kapton膜进行高温作用下单轴循环拉伸试验，探讨了经循环拉伸后膜材的力学性能变化规律，为这类新型膜材在充气可展结构中的应用提供参考.

1 单轴循环拉伸试验

1.1 试件尺寸

Kapton膜材参照塑料薄膜拉伸试验国家标准[15-16]，试验采用长条形试件，分别沿Kapton膜材MD向(沿膜材长度方向)和TD向(垂直膜材长度方向)裁切矩形条状试样(如图2和3)，具体裁切时按照图2所示每个方向选取试样距离整卷膜材端部大于等于3 m，距整卷膜材侧边部大于等于100 mm，均匀的在膜材卷上取样.同时，结合低温环境箱内部空间尺寸以及拉伸器行程，试件总长度为150 mm，宽度为25 mm，厚度25 μm，夹持端长25 mm，有效拉伸区域为100 mm×25 mm，夹持端采用2 mm厚的铝片进行加固，试件的尺寸设置见图4.

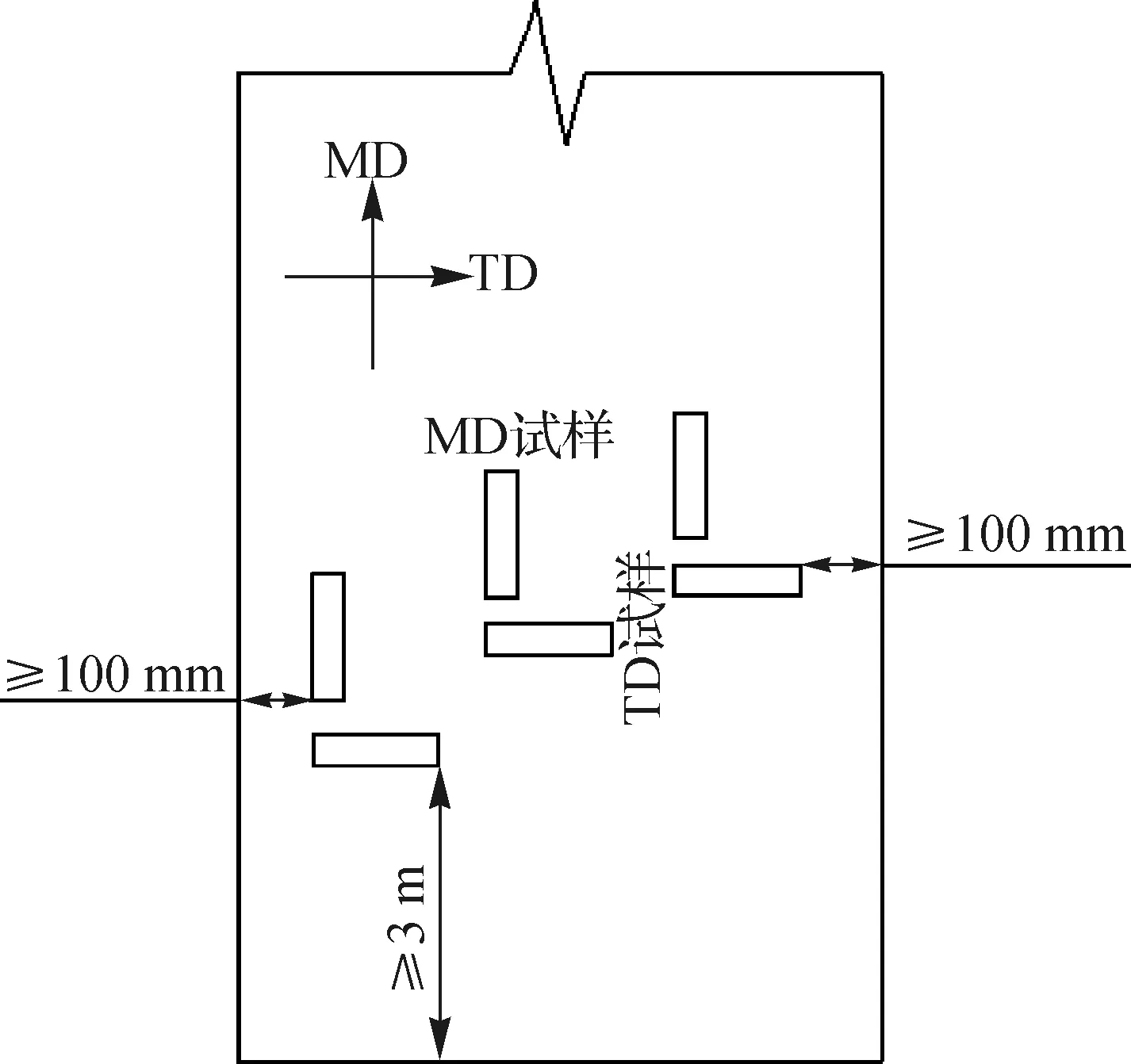
图2 Kapton膜片试样裁剪示意Fig.2 Trimmed specimens for Kapton foil

图3 Kapton膜材长条型拉伸试样Fig.3 Strip specimens of Kapton foils

图4 试样的几何尺寸Fig.4 Geometry of specimen

1.2 试验温度

试验共设置6种温度工况，分别为20 ℃、50 ℃、80 ℃、110 ℃、140 ℃、170 ℃.

1.3 试验设备及加载制度

试验设备采用INSTRON5965电子红外拉伸试验机(图5(a))，夹具采用手动楔形夹具，试验机最大载荷5 kN，带有高温环境箱(图5(b))，该高温试验采用电加热，将环境箱中的温度调节至预设温度.试验开始时，在夹具中央夹紧试样，使其纵向中心线通过夹持面的中心线，保证拉力中心线通过试样的中心线.将膜片试样放入高温环境箱，待其达到目标温度后，保持20 min，使其恒温稳定后开启试验机进行试样的拉伸，配置引伸计测量标线间的应变.拉伸初始时刻，首先对膜材进行预张拉，预张力大小约为3 N，接下来采用上述位移控制将试件常速拉伸至破坏，同步实时记录荷载-位移曲线.试验数据采集频率为20 Hz.试验采用三角波加载，循环加载5次，拉伸速率为10 mm/min，最大拉力为对应温度下1/4单轴拉伸强度，卸载时最小控制应力为1 MPa，具体数据见表1，考虑到Kapton薄膜力学性能的离散型，各组工况均选取5个试件.

图5 试验设备

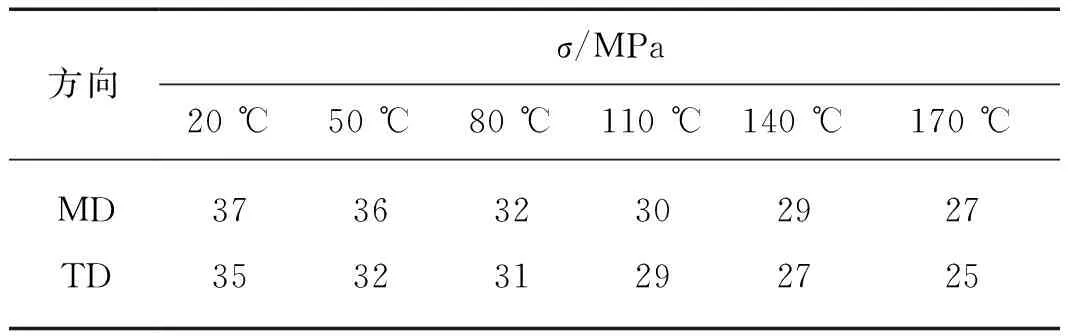
表1 不同温度下Kapton薄膜的1/4单轴拉伸强度

2 应力-应变关系曲线

各温度下单轴循环加载试件的应力-应变关系曲线如图6和图7所示，碍于篇幅这里仅列出3种温度工况下的应力-应变关系曲线.

图6 各温度下单轴循环加载试件的应力-应变关系曲线(MD)Fig.6 Relationships of stress-strain under uniaxial cyclic loading for different temperatures(MD)

图7 各温度下单轴循环加载试件的应力-应变关系曲线(TD)Fig.7 Relationships of stress-strain under uniaxial cyclic loading for different temperatures(TD)

由应力-应变关系曲线可得：各温度作用下的第一次加载曲线与对应温度作用下的单轴拉伸曲线一致，

即随着温度的增大，MD和TD试件的应变逐渐增大，且同温度作用下TD的应变大于MD；第一次加载曲线具有明显的非线性特征，试件第一次卸载后的应变大于相同加载应力(1 MPa)作用时所对应的应变量，因为试件产生了不可恢复的残余应变，其初次加卸载的残余应变均值以80 ℃工况为例，MD为0.304%，TD为0.503%.随着循环次数的增加，滞回曲线所围成的面积在逐渐减小，残余应变的增加量也在逐渐减小；5次循环后，随着温度由20 ℃增加至170 ℃，MD试件的残余应变由0.232%增至0.841%，TD试件的残余应变由0.303%增至1.05%.可见温度对Kapton膜材的残余应变有着显著的影响，分析认为随着温度的升高膜材会逐步被“烫软”，发生脆-韧转变，使得材料的脆性降低，韧性增强，因此最终会导致Kapton膜材在循环拉伸结束后，材料的残余应变量随着温度的升高而增大；以170 ℃工况下MD和TD的单轴循环拉伸结果为例，分析循环次数对Kapton膜材非线性特征的影响，选取各循环的加载上升段去除残余应变，得到两组应力-应变曲线(图8).由图8可知：随着加载次数的增加，膜材的非线性特征逐渐减弱，而线性特征逐渐增强，同时任一加载曲线与卸载曲线均不重合，这表明Kapton膜材具有明显的黏弹性和黏塑性特征.

图8 去除残余应变后单轴循环加载下试样的应力-应变曲线Fig.8 The stress-strain curvess of specimens without residual strain under uniaxial cyclic loading

3 弹性模量

为评价单轴循环加载对Kapton膜材弹性特性的影响，对加卸载阶段应力-应变曲线的割线(加载曲线的最低点和最高点的连线)斜率进行求解，将割线斜率近似等效为循环加载过程的弹性模量E，取5组试件试验结果的平均值[17-21]，以20 ℃工况为例分别讨论循环次数和试验温度对弹性模量的影响，具体数据如表2所示.

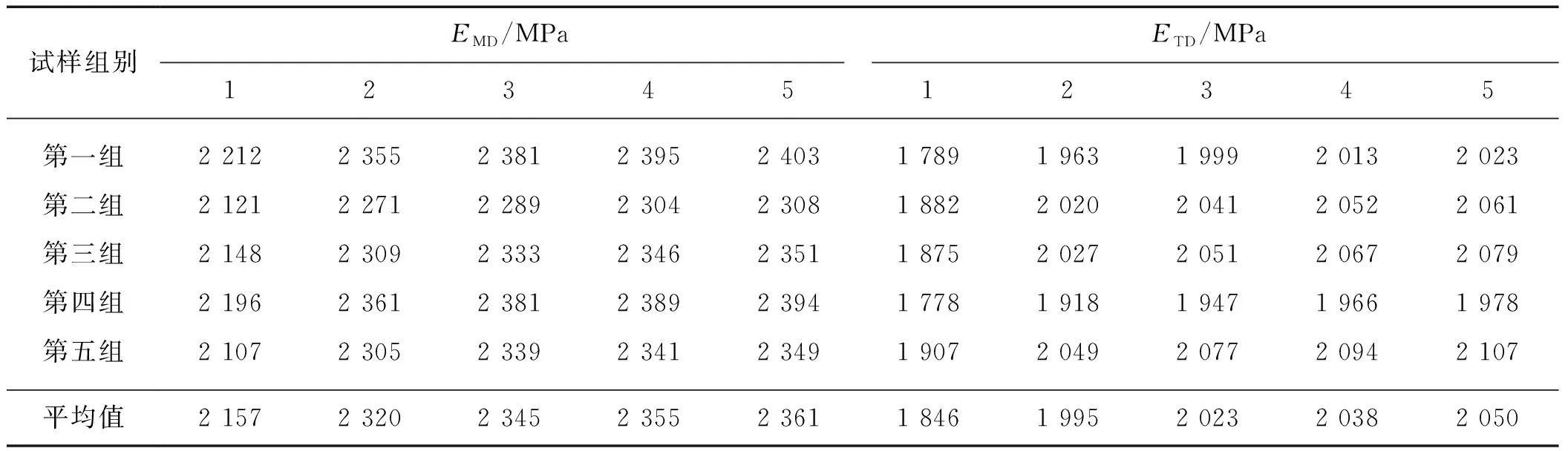
表2 20 ℃各组单轴循环加载弹性模量及其平均值

3.1 循环加载次数对弹性模量的影响

取20 ℃工况下的试验结果来进行分析，并由式(1)计算弹性模量增大幅度，

f={[E(i+1)-E(i)]/[E(5)-E(1)]}×100%,

(1)

其中f为增大幅度，E(i)为第i次循环时的弹性模量.各循环次数对应的弹性模量及其增大幅度如表3所示.

从表3中数据可得，随着循环次数的增加，MD和TD的弹性模量均大幅度提高，第5次循环的弹性模量同第1次循环的弹性模量相比，MD增大了204 MPa，TD增大了207 MPa，分别增大了9.46%和11.21%.相邻循环间的增大幅度f的最大值在第2次循环时出现，MD和TD的增大幅度分别为79.93%

表3 单轴循环加载弹性模量及其增幅

和72.08%，随着循环次数的增大，相邻循环间弹性模量的增大幅度逐步减小，趋于平缓.通过拟合式(2)和式(3)分别对MD和TD单轴循环加载弹性模量进行预测，MD经过8次循环加载后弹性模量增大幅度为0.81%，TD经过8次循环加载后弹性模量增大幅度为0.96%，表明Kapton膜材在循环加载8次后弹性模量可以认为达到稳定.

EMD=e[7.775-0.034/(n-0.653)]，

(2)

ETD=e[7.639-0.065/(n-0.448)]，

(3)

n表示循环次数.

为验证上述预测的可靠性，20 ℃工况下对膜材试样进行8次单轴循环加载试验，数据如表4所示.

由表4可以看出经8次循环加载后，MD和TD循环加载弹性模量增大幅度分别为0.87%和0.71%，故可以认为Kapton膜材试样在单轴循环加载8次后弹性模量达到稳定.

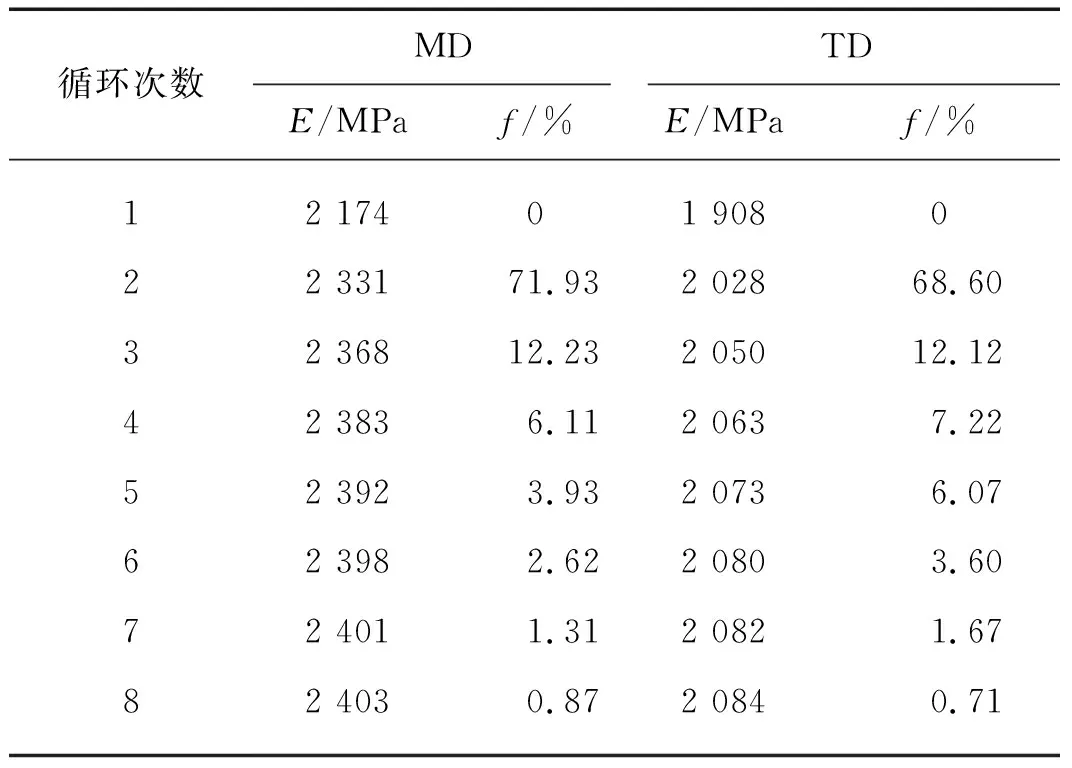
表4 8次单轴循环加载膜材的弹性模量及其增幅(20 ℃)

3.2 高温对弹性模量的影响

取各温度下第5次循环加载的弹性模量来进行分析，各温度下弹性模量分布见图9.随着温度的增大，MD和TD的单轴循环加载弹性模量均大幅减小，170 ℃下单轴循环拉伸的弹性模量同20 ℃下的弹性模量相比，MD减少了965 MPa，TD减少了875 MPa，分别减小了40.87%和42.62%.可见温度的变化对MD和TD的影响效果较为一致，但MD的弹性模量大于TD的弹性模量，分析认为造成该差异的原因是Kapton薄膜在制备过程中的牵引、固化等制作工艺和膜材微观分子链择优取向[22]的共同作用导致的.断裂的分子理论认为，材料发生破坏时，微观上要发生相应的某种分子运动或向活化态的转变，随着温度的升高，膜材内部分子热运动加剧，分子键能减弱，受到外力时易发生断裂，表现为材料强度和模量的下降；反之随着温度的降低，分子运动减弱，分子键的作用加强，在固定的时间间隔内，将使实现这种分子运动或转变的机会减少，从而使材料的强度和模量提高.故随着温度的升高，Kapton膜材的弹性模量呈现出逐步降低的结果，通过式(4)和式(5)分别拟合温度对Kapton膜材MD和TD单轴循环拉伸弹性模量的影响.

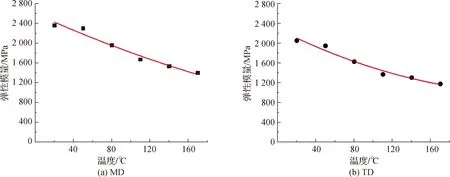
图9 单轴循环拉伸弹性模量与温度之间的关系Fig.9 The relationship between modulus and temperature under uniaxial cyclic loading

EMD=0.01T2-8.77T+2 598.15,

(4)

ETD=0.018T2-9.66T+2 288.85，

(5)

其中T表示温度工况.

4 棘轮应变

棘轮应变表示材料在承受循环荷载作用时所产生的渐进变形，对结构的形状和受力等有着影响，是实际工程中需要考虑的重要问题之一[23].Kapton膜材在单轴循环拉伸过程中，最大加载应力作用下的变形明显大于最小加载应力下的变形(如图10(a)所示)，这表明棘轮应变与材料所受应力状态有关.本文主要讨论温度对棘轮应变的影响，第5次循环加载完成后Kapton薄膜的最大棘轮应变εmax和最小棘轮应变εmin随温度的变化规律如图10(b)和(c)所示.

从图10(b)和(c)中可以看出，随着温度的升高，Kapton膜材单轴循环拉伸的最大棘轮应变εmax和最小棘轮应变εmin都随着温度的增大而增大，MD方向上εmax的变化范围在1.82%～2.83%，均值为2.25%，εmin的变化范围在0.23%～0.97%之间，均值为0.54%；TD方向上εmax的变化范围在1.97%～3.22%，均值为2.66%，εmin的变化范围在0.30%～1.10% 之间，均值为0.77%，可见温度对TD方向上的棘轮应变影响更大.

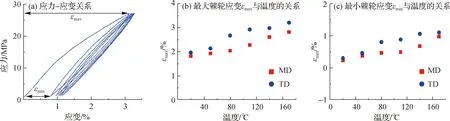
图10 最大棘轮应变εmax和最小棘轮应变εmin与应变、温度的关系

5 滞回环面积

Kapton膜材具有黏弹塑性特征，在循环荷载的作用下，由于黏滞效应导致产生能量耗散，加载段曲线同卸载段曲线没有重合在一起，二者所围成的面积称为滞回环面积，其大小能够较为直接的反映出能量耗散的情况，是分析结构在承受循环荷载过程中的刚度退化、变形特征和能量耗散问题的重要依据.计算原理见图11.

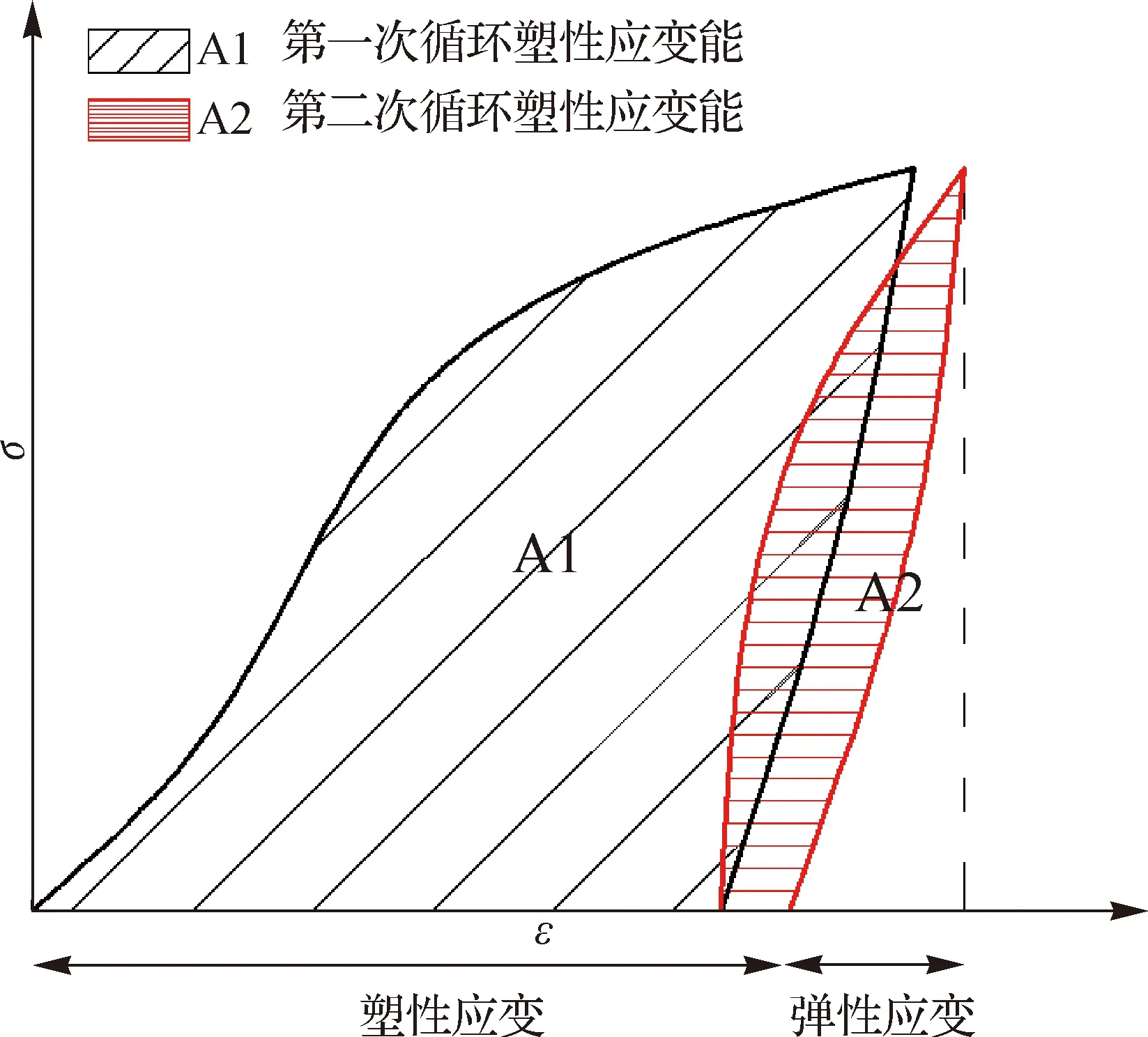
图11 滞回环面积计算示意图Fig.11 Hysteresis loop area calculation

不同温度下Kapton膜材滞回环面积与循环次数的关系如图12所示，从图中可以看出滞回环面积A随着循环加载次数的增加而减小，尤其是第1次循环至第2次循环的下降幅度最大，MD和TD的平均下降幅度分别为47.30%和47.81%；此外随着循环次数的增加，滞回环面积的减小幅度逐渐降低并趋于稳定，第5次循环完成后，MD和TD的平均下降幅度仅为7.42%和7.16%.这表明随着循环次数的增加，Kapton膜材主要产生可恢复的弹性应变能，而塑性应变能则逐步减小.随着温度的升高，同一循环过程中，滞回环面积也是增大的.首次循环过程中，将170 ℃工况下的滞回环面积同20 ℃工况下的滞回环面积进行比较发现，MD增大幅度为176%，TD增大幅度为140%.可见温度对Kapton膜材的耗能性能有着显著的影响，温度升高，在原有能量耗散的基础上，Kapton膜材内部分子热运动加剧进一步对能量进行消耗，宏观上表现为膜材塑性变形性能提高.

图12 不同温度下Kapton膜材滞回环面积与循环次数的关系Fig.12 The relationships between hysteresis loop area and cycles for Kapton foils under different temperatures

6 结 论

1) Kapton膜材在循环加卸载完成后，产生了不可恢复的残余应变；温度对Kapton膜材的残余应变有着显著的影响，高温环境下膜材发生脆-韧转变，残余应变量随着温度的提高而增大；随着循环次数的增加，膜材的非线性特征逐渐减弱，而线性特征逐渐增强，同时任一加载曲线与卸载曲线均不重合，这表明Kapton膜材具有明显的黏弹性和黏塑性特征.

2) MD和TD的弹性模量随着循环次数增大均大幅度提高，但相邻循环间弹性模量的增大幅度逐步减小，趋于平缓.通过建立拟合公式对Kapton膜材单轴循环加载弹性模量进行预测，Kapton膜材在循环加载8次后弹性模量可以认为达到稳定；随着温度的升高，Kapton膜材的单轴循环加载弹性模量均大幅减小，通过建立拟合公式来表示Kapton膜材单轴循环加载过程中温度和弹性模量之间的关系.

3) Kapton膜材单轴循环拉伸的最大棘轮应变εmax和最小棘轮应变εmin均随温度的升高而增大；随着循环次数的增加，Kapton膜材的滞回环面积逐渐减小，产生可恢复的弹性应变能，而塑性应变能则逐渐减小；温度的升高使得膜材内部分子运动加剧，Kapton膜材的耗能性能提高，宏观上表现为塑性性能提高，滞回环面积随温度的增大而增大.