带伸臂超高层建筑风振控制方法对比分析

钟 原，张建国，张建霖

(厦门大学建筑与土木工程学院，福建 厦门 361005)

随着结构理论、施工技术以及新材料的发展，超高层建筑已成为现代城市中必不可少的元素，各大城市的“最高建筑”记录正在不断刷新，对结构以及相应的振动控制措施也有更高的要求.超高层建筑的柔度大、阻尼小，风荷载通常会成为此类风敏感性建筑的控制性因素.传统的高层建筑抗风设计通过增强截面、设置加强层等方法提高结构自身刚度以达到减小位移的目的，但却使建筑造价大量增加，且存在诸多缺陷[1-3].

1972年，美籍华裔学者姚治平首次提出了结构控制的概念，通过在结构上安装各类控制装置，来减弱或抑制结构由于动力荷载作用引起的响应.经过数十年的发展，振动控制技术现作为一种经济可行的技术，已成为结构抗风设计的常用方法，其中调谐质量阻尼器(tuned mass damper，TMD)系统以及耗能阻尼器作为研究热点，诸多国内外学者[4-9]展开系列研究，取得了丰富的研究成果；台北101大楼在结构87～92层以及101层以上尖塔部分安装TMD后经历多次强台风的实测检验，结构均满足舒适度要求[10]；菲律宾Saint Francis香格里拉塔实践了竖向伸臂加强层阻尼体系[11]，在加强层悬臂墙端头连接处垂直设置了16个耗能阻尼器，分析结果显示，该方案可以大幅度降低结构的风振响应；周云等[12]提出将加强层桁架中的刚性支撑用耗能构件(支撑+阻尼器)代替，形成水平伸臂加强层阻尼体系，并验算该体系在地震作用下可以通过阻尼器来耗散能量，有效达到减震的目的；有多位学者[13-15]采用通用有限元软件建模分析了带有伸臂加强层阻尼体系的超高层结构风振控制效果，结果表明该体系对脉动风荷载作用下的结构响应也有良好的耗能减振作用；目前的研究[16-17]对带伸臂超高层建筑的风振控制也提出了更多优化理论方法.

本文在已有研究的基础上，对比分析TMD与伸臂加强层阻尼体系对带有伸臂加强层的超高层建筑的风振控制效果，并探究两者混合控制的减振效果.选取一栋304.2 m的超高层框架-核心筒结构为算例，应用ETABS软件建立其三维空间有限元模型，取风洞试验数据获得的风荷载时程函数对结构设置4种不同的振动控制方案进行模拟计算.

1 振动控制模型

1.1 风振控制方程

对于带有阻尼器的超高层结构，在水平脉动风荷载的作用下，结构的控制方程[18]可表示为：

(1)

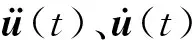
对于带有TMD的超高层结构，设TMD的质量、阻尼、刚度系数分别为mT、cT、kT，TMD系统设置在第j层时，位置向量为Hj，则式(1)可表示为：

(2)

即为TMD系统的控制方程.

根据能量平衡原理，在式(1)左右两端同乘相对位移向量duT(t)，并在时域上积分，可得：

(3)

式(3)即为相对能量方程，表示任意时刻的结构能量，可写为：

Ein=Ek+Ec+Ee+Etran,

(4)

(5)

其中：

(6)

(7)

(8)

(9)

(10)

(11)

在风振控制体系中，结构一般处于弹性状态，此时，Ec约占风振总输入能量的5%，可忽略不计，结构主要依靠阻尼器体系耗散输入结构的风能量，即：

(12)

根据上述推导可得出结论：合理地设置TMD或其他阻尼器的位置和参数，使阻尼器体系耗散能量增大，以此来降低主结构吸收的能量，有效保障主结构的安全性、适用性和舒适性.

1.2 振动控制模型

伸臂加强层阻尼体系的振动控制模型可以简化为由框架-核心筒与伸臂加强层中布置的阻尼器组成的模型(图1)，结构受到风荷载作用时，利用层间位移差使得布置在加强层处的阻尼器产生位移，耗散能量.

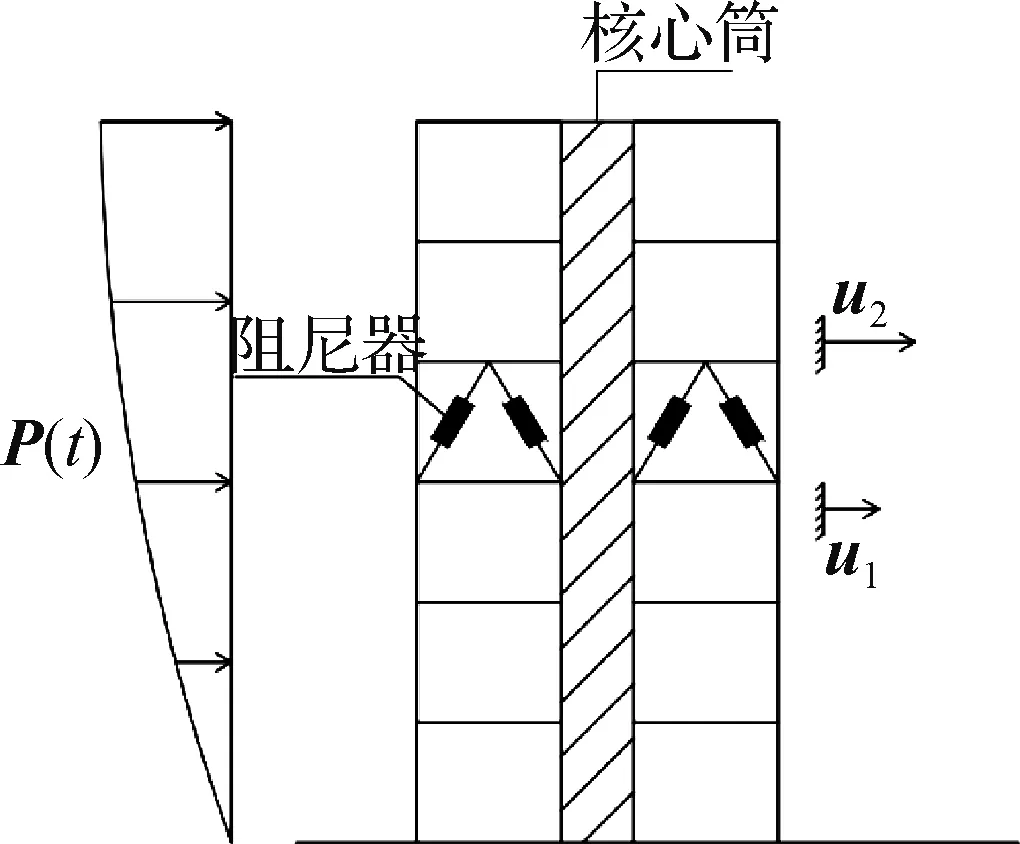
图1 伸臂阻尼体系模型Fig.1 Damped outrigger system model

超高层建筑结构多自由度体系在顺风向的脉动风荷载作用下的TMD振动控制模型见图2.根据经典参数设计理论[19]，对于给定的TMD质量，系统最优频率比λ和最优阻尼比ξopt满足：

图2 TMD控制模型Fig.2 TMD control model

(13)

其中：λ=ωt/ω1，为频率比，ωt为TMD的固有频率，ω1为主结构第一自振频率，μ=mT/M为质量比，M为主结构第一振型广义质量，ξopt为TMD的最优阻尼比.

2 工程算例

2.1 工程概况

选取的工程算例为框架-核心筒结构，地上69层，地下3层，主体结构高304.2 m，属于超B级高度；B类地面粗糙度，基本风压取0.55 kN/m2，7度抗震设防烈度，Ⅱ类场地.建筑平面布置为正方形，尺寸为43.2 m×43.2 m，核心筒底层平面尺寸为22.8 m×22.8 m，高宽比H/B=7；建筑立面造型规则，为简化计算，取消底部裙房.1～4层层高均为6 m，标准层层高4.2 m，结构16、32、48、64层设有避难层，避难层层高6 m.框架柱均采用型钢混凝土柱，柱、剪力墙混凝土强度等级为C60，楼板、次梁混凝土强度等级为C40，相邻框架柱之间以及框架柱与核心筒之间采用H型钢框架梁连接.

根据《高层建筑混凝土结构技术规程》(JGJ3—2010)的相关规定(下文简称《高规》)[20]，本建筑物结构顶点加速度限制取0.25 m/s2.

2.2 风荷载选取及计算

本文取用风洞试验数据用于研究结构在水平风荷载作用下的动力响应[21].在获得各风向角作用下的表面风压时程实验数据后，通过MATLAB程序将其转化为实际结构对应高度上的风压值，通过线性插值求得实际结构各楼层的风压值，并进一步求得作用在实际结构各楼层的、轴向和扭转向的风荷载时程，最后将模型的采样频率转化为实际结构的风荷载作用频率，求得实际频率为3.198 Hz，实际结构的风荷载周期为0.312 7 s.由现有结构计算结论[13]，0°风向角时，水平风荷载所引起的动力响应作用显著大于其他风向角，故本文取0°风向角进行后续计算.图3风向角为0°时作用在实际结构顶层处的、轴向和扭转向的风荷载时程记录.

图3 风荷载时程记录图Fig.3 Wind load time history record chart

3 结构计算模型

3.1 三维有限元模型

该工程采用Etabs2017软件建立三维有限元模型，剪力墙采用壳单元，楼板采用膜单元，梁、柱采用空间杆单元.模型共有23 151个单元，5 721个节点.无控制状态下结构的基本参数如表1所示.

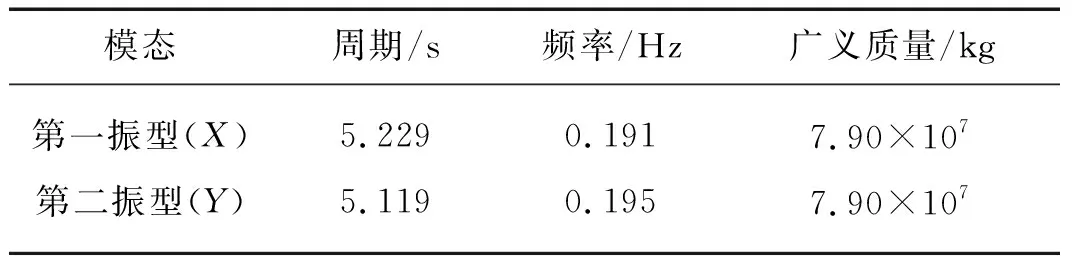
表1 无控制结构基本参数

3.2 阻尼器模拟单元

当采用ETABS有限元模型进行分析时，可将控制装置等效模拟为如图4所示的Damper单元，即由弹簧k和阻尼c串联而成的Maxwell计算模型，其非线性力-变形关系为：

(14)

d=dk+dc.

(15)

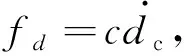
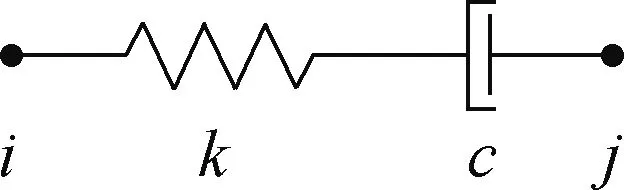
图4 Maxwell模型
Fig.4 Maxwell model

3.3 TMD模拟单元

如图5所示，TMD由质量块MT、弹簧KT以及阻尼CT组成，其中阻尼CT采用3.2节所述的Maxwell计算模型.将弹簧模型与Maxwell模型并联组合，在通过调整Maxwell模型中的k，c之间的比值，从而实现TMD中的阻尼CT以及对应的TMD参数调整.选取TMD质量为800 t，质量比为1%，根据第一节式(13)，确定TMD最优频率比和最优阻尼比.

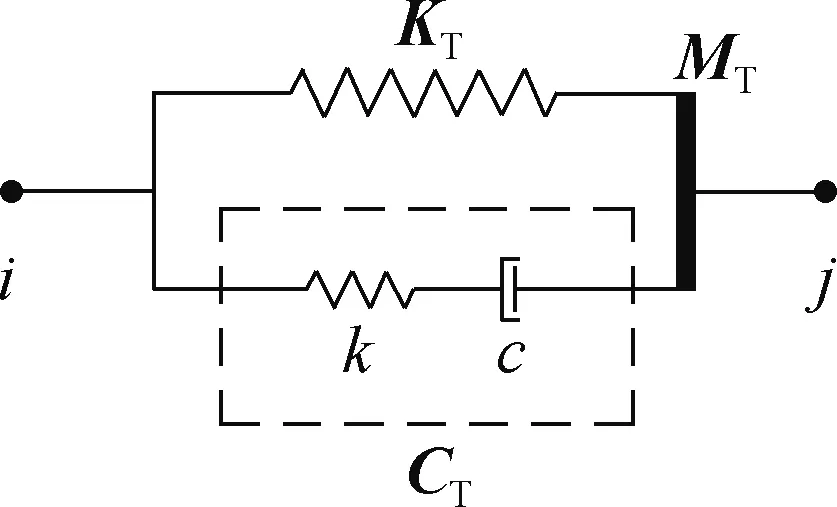
图5 TMD模拟示意Fig.5 Simulation of TMD

4 风振控制方案及效果

4.1 控制方案设置

对伸臂加强层的布置位置参照《高规》，当布置1个加强层时，可设置在0.6倍房屋高度附近；当布置2个加强层时，可分别设置在顶层和0.5倍房屋高度附近；当布置多个加强层时，宜沿竖向从顶层向下均匀布置.

采用无控制模型作为对照，对结构设置4种控制方案.控制方案参照类似超高层建筑已有的科研成果[2,7,13]，并结合建筑结构自身特点来布置.

方案一：在结构顶层设置重为800 t的TMD.

方案二：在结构的32层、64层伸臂加强层处各设置16个阻尼系数为500 kN·s/mm的非线性黏滞阻尼器，以人字形安装的形式代替伸臂桁架的斜撑.

方案三：在结构的32层伸臂加强层处参照方案二设置16个阻尼器，同时按照方案一在结构顶层设置TMD.

方案四：在结构的32层、64层的伸臂加强层处参照方案二设置阻尼器，同时按照方案一设置TMD.

4.2 风振控制效果

根据上述4种方案进行计算，得出各工况下的结构响应.根据计算结果，无控制状态下结构顶层加速度为0.289 5 m/s2，无法满足规范对舒适度的要求，所以有必要在结构上设置适当的减振方案.以结构顶层的位移和加速度作为振动控制目标，结构的减振效果如表2所示.图6为无控结构与采取不同风振控制措施结构沿高度方向变化的层位移、速度、加速度对比曲线.结构耗能情况对比见图7.

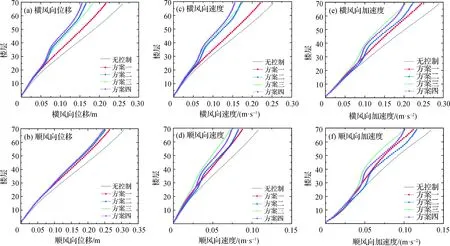
图6 各方案位移、速度、加速度对比Fig.6 Displacement, velocity, acceleration comparison

图7 各方案耗能情况对比Fig.7 Energy dissipation comparison

表2 不同方案下结构顶层的减振效果

加设了风振控制措施后，结构的动力响应都有不同程度的衰减，耗能减振装置有效耗散了部分能量.从位移控制效果来看，方案一设置TMD对结构位移控制有一定作用，但效果较其他方案稍弱，阻尼器对结构位移控制的效果更为显著，从结构耗能情况的对比中也可以看出，带有阻尼器的方案耗能效果更佳.在方案二设置两道伸臂加强层阻尼体系的控制效率就可达到36.34%，但加上TMD后形成的方案四控制效率增幅较小，为40.34%.实际工程中受限于构件承载力和构造等方面的影响，TMD质量不能无限放大，若达不到理论的最优值而无法满足控制要求，可以加设阻尼器，如方案三和四.

在速度和加速度控制方面，各方案控制效果良好，均可使主体结构在风振作用下满足安全性、舒适性的要求.方案三对结构设置单层伸臂加强层阻尼体系与TMD的混合控制效果比单一设置的方案控制效果更佳；但随着阻尼器数量的增加，如方案四在方案三的基础上增加一层伸臂阻尼体系，在顺风向的速度和加速度的控制方面对控制效率没有明显提升，并且增加阻尼器的使用也会导致成本的增加，对结构加强层处的空间利用、构件的布置也有更高的要求.

5 结 论

本文所选择的算例作为典型的带伸臂加强层框架-核心筒结构，总高度304.2 m，结构布置无明显不规则，具有一定的代表性，在此基础上通过三维空间有限元模型的计算，分析不同控制措施下的控制效果，可作为类似结构风振控制方案设计的一种参考，有如下结论：

1) 在结构加强层设置非线性黏滞阻尼器代替伸臂桁架斜撑，形成的伸臂加强层阻尼体系以及TMD控制体系都能够有效减弱结构动力响应，耗散能量，以满足规范对结构舒适度的要求，但TMD控制效果较其他方案稍弱，由于本算例取1%质量比的TMD进行计算，随着质量比增大，TMD的减振效果可以进一步优化.

2) 混合控制方案仅从控制效果来看在本文给出的四种方案中最优.在位移控制方面，随着阻尼器数量的增加控制效果更好；但在速度和加速度控制方面，混合控制方案中阻尼数量的增加对控制效果没有明显提升，故在风振控制设计优化中，仅增加阻尼器数量效率有限，应综合考虑更多方案.

3) 在类似结构的超高层建筑减振方案的选择上，若TMD控制效果无法满足要求，可以在伸臂加强层处加设阻尼器来进一步优化控制，并且节约建筑空间以满足安全、经济等各方面要求.