基于氟化钙光学谐振腔的声传感机理研究*

邢恩博， 邢 彤， 戎佳敏， 唐 军

(中北大学 仪器与电子学院，山西 太原 030051)

0 引 言

回音壁模式(whispering gallery mode,WGM)光学谐振腔由于具有高品质因数Q、较小的模式体积以及易于小型化集成的特性，是具有重要应用潜力的光子平台[1～5]。随着现代微细加工的发展，高Q值光学谐振腔材料[6,7]也有了更多的选择，具有超高透过率的光学晶体材料以其优越的光学特性、高可控性的加工形状、可精确设计的几何特征以及超高品质因数等优点备受瞩目。目前已经开发了基于氟化钙(CaF2)[8]、氟化钡(BaF2)[9]、铌酸锂(LiNbO3)[10]、氟化镁(MgF2)[11]等材料的光学微腔，其中，氟化钙晶体腔理论Q值可达到1013量级[12]，实验Q值突破1011量级[13]。以上优点使得光学晶体谐振腔在超高灵敏度物理量传感领域极具竞争力[14～16]。

传统声学传感器受运动部件机械共振频率的约束，往往在声学探测灵敏度或声频率响应范围面临挑战，而基于光学谐振腔的声学传感器突破了传统以运动部件(如振动膜片)为敏感单元的传感结构[17～19]，同时具有抗电磁干扰、灵敏度高、动态范围大等优点，在近些年来逐步发展起来[20～22]。目前,基于光学谐振腔已经报道了各种类型的光学声传感器，比如：南京大学姜校顺课题组报道了一种紧凑、高灵敏度的悬臂式微谐振器系统[23]，其频率响应范围覆盖0～6 kHz，在900 Hz下的噪声等效压力为52 μPa/Hz1/2；暨南大学李朝晖课题组报道了微气泡谐振腔与光频率梳结合用于高精度空气耦合的超声探测器[24]，微泡腔品质因数Q为3×107，在165 kHz时噪声等效压力为4.4 mPa/Hz1/2；中北大学薛晨阳课题组利用高Q的F-P标准具，得到177.6 mV/Pa的灵敏度和20 Hz～70 kHz的频率响应范围[25]。

尽管基于光学谐振腔的声学传感已经取得了进展，但是超高灵敏度方面，光学谐振腔的优势还没有被充分展示。氟化钙晶体谐振腔具有更高的Q值和更窄的光学谐振峰，对应更高的频率检测灵敏度，因此是优秀的声学传感平台。然而,对于具有较高杨氏模量的氟化钙晶体而言，其声学检测机理尚不明确，因此本文基于氟化钙盘型谐振腔，从空气密度引起的折射率变化、弹光效应诱导有效折射率改变和谐振腔结构形变开展声传感灵敏度机理研究。计算结果表明，声压诱导谐振腔结构形变是感知声学辐射压力的主要因素，以实验室器件为标准，达到了1.196×10-10Pa-1，对应的谐振峰波长响应为4.63×10-7nm/Pa。而空气密度引起的折射率变化在WGM盘型微腔中的作用最小。通过优化结构参数，结合调制解调器技术，可以较容易地实现V/Pa量级的声学灵敏度，因此，本文为超高灵敏度声学微腔传感提供理论支撑。

1 理论仿真分析

1.1 氟化钙谐振腔声传感结构

根据耦合模理论，回音壁模式的共振波长可以从WGM腔内的驻波条件下推导出

mλr=2πRneff

(1)

式中R为氟化钙谐振腔的半径，neff为有效折射率，m为谐振级数，λr为谐振波长。基于氟化钙晶体腔的声传感器结构如图1(a)所示，氟化钙晶体谐振腔可以通过锥形光纤或棱镜进行光学能量注入和读出。喇叭发出不同频率和不同强度的声音作用于氟化钙晶体谐振腔，使得谐振谱的谐振波长发生漂移，进而得到不同声压下谐振波长的变化量。由于声压导致的氟化钙谐振腔的波长漂移量比较少，利用调制解调技术，可以实现将微弱的波长漂移转换为光强变化，从而得到声传感器灵敏度(V/Pa)，如图1(b)所示。

图1 基于氟化钙晶体腔的声传感示意

1.2 声传感机理研究

声波传播的本质是流体或固体内介质疏密不断交替变化，常使用体积元内的压强、密度、质点速度等变化量进行表征。其中,声压即体积元受声扰动后压强的变化量，存在声压的空间称为声场。氟化钙晶体腔光声传感器是利用晶体腔光纤耦合作为敏感单元，传感理论分为以下三种：1)声压引起谐振腔的半径发生改变；2)声压引起应变，通过弹光效应改变氟化钙晶体腔材料折射率，进而改变有效折射率；3)声压改变了晶体腔光声耦合倏逝场的空气密度，使得空气折射率发生改变，进而导致谐振波长漂移。下面就这三种理论分别进行分析。

1)结构形变导致谐振腔尺寸改变

首先就第一种理论进行分析，利用有限元仿真分析，建立晶体腔模型，通过对氟化钙晶体谐振腔上表面施加不同的声压，观察谐振腔半径的变化。参考本实验器件参数，氟化钙盘型腔厚度为0.5 mm，直径为5 mm，下方支撑是直径为3 mm铜柱，两者的杨氏模量分别是75.8 GPa和110 GPa。对不同声压下(0～10 Pa)谐振腔的半径变化进行线性拟合，得到声压与谐振腔半径存在线性关系，结果如图2所示。图2左边为1 Pa声压导致晶体腔位移示意图，右边为不同声压下通过拟合得到的半径变化量，其斜率为2.99×10-10mm/Pa。由于氟化钙盘型腔的直径为5 mm，可以得到不同声压下半径变化率为1.196×10-10Pa-1。

图2 结构形变导致谐振腔尺寸变化仿真

2)弹光效应引起有效折射率改变

以上述模型为参考，同样地，通过对氟化钙晶体谐振腔上表面施加不同的声压，得到应变的变化，再利用弹光效应计算获得氟化钙晶体腔折射率的改变，最后，得到声压与折射率的关系。压力引起的谐振腔折射率变化遵循以下公式

(2)

图3左边为声压导致晶体腔应变示意图，右边为通过弹光效应得到的声压与晶体腔折射率的关系图，可以看出声压与折射率存在线性关系，其斜率为-0.74×10-11Pa-1，可以得到不同声压下折射率变化率为-0.52×10-11Pa-1

(3)

根据式(3)可以得到谐振腔结构尺寸变化对应的波长漂移为1.85×10-7nm/Pa，弹光效应导致折射率变化引起的谐振波长漂移为-8.06×10-9nm/Pa，两者共同作用的总波长漂移为1.77×10-7nm/Pa。

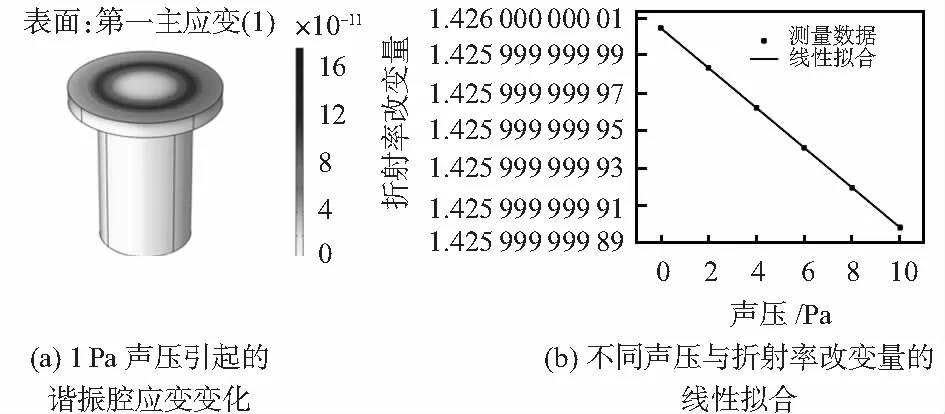
图3 弹光效应引起有效折射率改变仿真

3)空气折射率变化引起谐振波长漂移

当声音在空气中传播时，空气密度发生变化，进而导致其倏逝场折射率也会发生改变，声压与空气折射率的变化公式

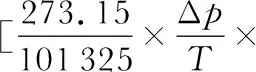
(4)

其中，谐振腔波长λ=1.55 μm，温度T=293.15 K，声压Δp=1 Pa。再根据空气折射率变化导致的谐振波长漂移，如式(5)所示

(5)

式中ζq为埃里函数的第q阶0，空气折射率ns与声压有关，谐振腔折射率nr=1.426，l为模式数。

通过公式计算得到图4，谐振波长漂移为1.54×10-9nm/Pa。可以看出，在以固体材料为主的WGM盘型谐振腔中，声压导致的空气折射率变化，进而引起谐振腔波长漂移是影响最小的因素。相比于F-P谐振腔声压传感机理，声压能够实现F-P腔内的空气介质密度变化，因此,直接影响谐振腔光学传输谱;而对于氟化钙盘型谐振腔，空气密度的变化没有直接作用于腔体，而是通过周围折射率变化间接的影响到谐振腔的有效折射率，因此,调制效率降低了几个数量级。通过对三种传感理论进行分析和比较，谐振腔半径改变量比谐振腔折射率以及空气引起的谐振波长漂移大2个数量级，所以,得到基于氟化钙谐振腔的声传感器主要来源于谐振腔半径的改变量。

图4 空气折射率改变共振模式漂移计算

2 传感器结构优化

通过对上述三种影响机理的分析，得到了声压诱导谐振腔半径改变量是主要因素，接下来,利用有限元仿真，分别对不同的铜柱半径与不同的谐振腔厚度进行了仿真分析，结果如图5所示。

图5 高灵敏度声传感的结构参数优化

图5(a)表明，铜柱半径从0.5 mm增加到2.5 mm，谐振腔半径变化从7.2×10-6mm降低到8.56×10-7mm。这是因为谐振腔形变主要来源于盘的边缘，而支撑结构越接近谐振腔直径，对于谐振腔尺寸变化的抑制越强烈，当谐振腔直径大于等于支撑铜柱直径时变化量最小。相应的,应变的变化规律也类似，但是变化量更小。图5(b)计算了谐振腔厚度对于两种传感机理变化量的影响，计算结果与预测一致，即，谐振腔厚度越小变化越明显，但是这里需要注意的是，当盘的厚度下降到0.3 mm以下时，该因素的影响就不再明显。对于实际加工而言，加工难度是随着厚度的减小而提高的，因此该优化对于实际加工具有重要的指导意义。图5(c)表明，谐振腔Q从107增加到1011，声传感器灵敏度从6.372 mV/Pa增加到63.72 V/Pa。这是因为谐振腔Q越高，线宽越窄，其对应的线性区域的斜率也就越大，当外界声信号作用于该区域时，微小的扰动就可以产生相当大的变化，也即对应高的灵敏度。因此，通过提高谐振腔Q可以有效提高氟化钙声传感器的灵敏度。

3 结 论

本文以超高Q值氟化钙晶体谐振腔为基础，通过外部声学压力仿真，对三种声学传感进行了理论计算和结果分析。计算结果表明:谐振腔半径改变量相比于其他两种机制更明显，即高杨氏模量的氟化钙晶体谐振腔的声传感机理主要来源于谐振腔半径的变化量，进一步引起谐振波长的漂移。同时，还通过支撑结构半径及谐振腔的厚度进行了仿真优化，结合实验室调制解调参数，实验室有望实现V/Pa量级的高灵敏度声学传感器件，本文的结果为小型集成化的高灵敏度声学传感器件提供了参考。