例谈数量积性质在竞赛题中的应用
2022-07-14吴侃男
高中数学教与学 2022年11期
吴侃男
(浙江省金华市浦江县中山中学,322200)
数量积及其性质是平面向量的重点内容,在数学的许多方面应用广泛.
由数量积的定义与向量模的知识,我们不难得到如下的向量不等式:设a,b是非零向量,则a·b≤|a·b|≤|a||b|,当且仅当a,b共线时等号成立.特别地,a·b≤|a||b|,当且仅当a,b同向时等号成立.本文举例介绍数量积的上述性质在数学竞赛题求解中的应用,给人以意想不到的解题效果.
一、比较大小

(A)M>N(B)M (C)M=N(D)不能确定 故选A. 当x=1时,方程不成立,故x>1. 解要证明x-2y≤200,而需证x≤2(y+100). 综上,得证. 解依题意,可得(x-1)2+(y-2)2=4. 由|a||b|≥a·b,可得 ≥(98-15cosθ-20sinθ)2. 所以|b|2=(6-5cosθ)2 综上,当点Q的坐标为(3,2)时,P,Q两点间的距离最小.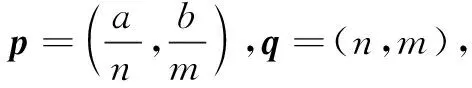
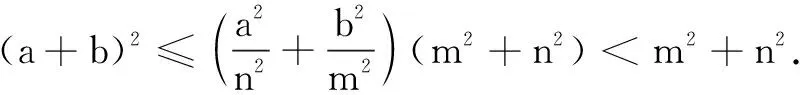
二、解方程


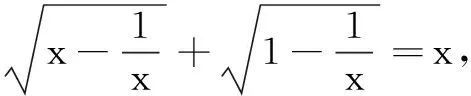

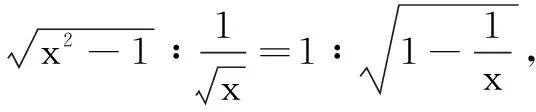
三、证明不等式

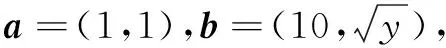
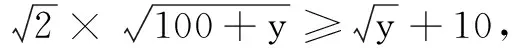

四、求函数的最值

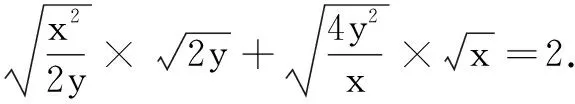

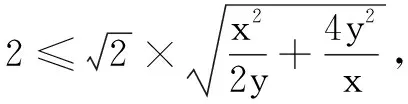

五、求函数的值域
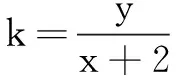


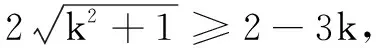

六、处理几何最值问题