均值代换法在解题中的几类应用

刘家新

(湖南省常德市澧县第一中学，415599)

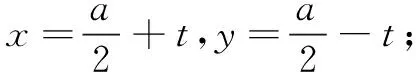
一、求代数式的值

例1已知实数a,b,c满足a+b+c=0,a3+b3+c3=0,求a5+b5+c5的值.

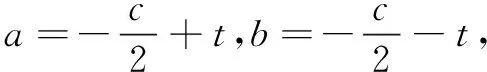
若c=0，则a=-b,此时有a5+b5+c5=0.

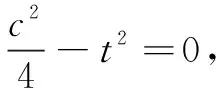
综上，a5+b5+c5的值为0.

评注本题中有三个变量两个等式,看似无法求解.此时我们转换观察问题的角度,视c为常数,运用均值代换法进行求解,方法新颖,过程简洁,令人耳目一新.

二、解方程

例2解方程

评注本题是一道无理方程,若直接求解,过程相当冗繁.而应用均值代换法将无理方程转化为整式方程,能使问题得以顺利解决.

三、证明不等式

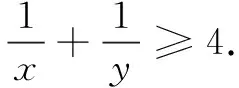
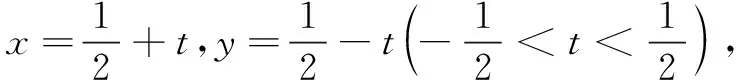
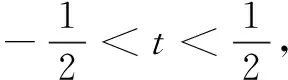
评注本题首先进行均值代换，并利用已知条件得到新元t的取值范围,然后对目标式左边变形、转化,并求得取值范围,从而使不等式获证.

四、求最值

评注本题利用均值代换法结合二元均值不等式求解,解法别具一格,充分体现了均值代换法的应用价值.

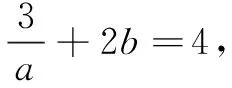
评注本题根据已知等式进行均值换元,代入目标式得到关于新元t的式子,再进行“1”的代换,运用配凑、变形,最后利用基本不等式求解.