深度学习中的权重初始化方法研究

邢彤彤，孙仁诚，邵峰晶，隋毅

（青岛大学计算机科学技术学院，山东青岛 266071）

0 概述

从MCCULLOCH等［1］提出神经网络的初步概念以及神经元的数学模型开始，针对神经网络的研究得到迅速发展。特别是深度学习［2］在图像领域的优秀表现，使其在机器学习［3］中脱颖而出。其中，卷积网络［4］的概念也越来越受到人们的关注和重视，尤其是在图像分类的处理中，卷积神经网络的表现非常突出。尽管训练越来越深的网络存在一些困难，但是卷积神经网络还是取得了较好的成绩，并且还在不断的优化、突破。

深度学习的本质就是学习、优化权重的值，使其达到一个最优解的状态。通过文献［5］提出的卷积神经网络可视化方式可清楚地观察到卷积神经网络每一层的权值情况，这其中需要更新权重的层，包括卷积层、BN 层和FC 层等。在寻找最优解的过程中，权重的初始化就是得到最优解的重要前提。如果权重初始化不合适，则可能会导致模型反向传播［6］失效，陷入局部最优解，使得模型预测效果不理想，甚至使损失函数震荡，模型无法收敛，即使用不同的权重初始化方法，能够直接影响模型的训练速度和最终精确度。因此，一个优秀的权重初始化方法是模型提升收敛速度和最终精确度的重要前提。

在深度学习领域中，卷积神经网络的权重初始化可以采取多种方式，如高斯（正态）分布初始化［7］、均匀分布初始化［8］、截断高斯分布初始化［9］（该初始化方法与高斯分布初始化相似，但分布形式为截尾分布）以及主成分洗牌初始化［10］等方法。其中，目前较为流行的权值初始化方法，如Xavier 初始化方法［11］和He 初始化方法［12］是在正态分布和均匀分布的基础上进行了改进。Xavier 初始化为了增加网络各层之间信息传播的流畅性，遵循了（正向传播）各层激活值方差和（反向传播）各层状态值的梯度方差在传播中保持一致的原则，通过均匀分布来进行权重初始化调整。He 初始化在Xavier 初始化的基础上稍加改变，遵循（正向传播）各层状态值方差和（反向传播）各层激活值的梯度方差在传播中保持一致的原则，在与ReLU 激活函数［13］的共同作用下，可以得到较好的收敛效果。然而，使用这两种权重初始化方法的网络依然存在训练时间长、需要数据量大的问题。文献［14］在实验过程中发现预训练模型［15］的权重参数分布可能存在幂律分布的现象，经过其后期验证得出预训练权重存在局部幂律的性质。

本文从Pytorch 中图像分类相关的预训练模型［16］入手，分析预训练模型的权重分布，提出一种标准化的对称幂律（Normalized Symmetric Power Law，NSPL）初始化方法。分析权重初始化面临的主要问题，研究预训练网络模型的权重分布，发现权重分布具备幂律分布的特征。在此基础上，基于标准化对称幂律分布，给出权重数据生成及初始化算法。

1 问题描述

1.1 权重初始化问题

权重有效初始化可以防止激活值在深度神经网络的正向传递过程中出现梯度爆炸或者梯度消失。模型经过权重初始化后，在训练、更新权重时主要会出现以下2 种情况：

2）如果初始权重太大，会导致输入状态也较大，对sigmoid 激活函数来讲，激活函数的值会变得饱和，从而出现梯度消失的问题。

1）如果初始权重太小，导致神经元的输入过小，随着层数的不断增加，会出现信号消失的问题，也会导致sigmoid 激活函数［17］中强调的丢失非线性的能力，因为在0 附近sigmoid 函数是近似线性的。

无论上述哪一种情况发生，损失梯度要么太大或要么太小，更新信息都无法有效地向后传递，网络则需要很长时间才能收敛。研究人员研究了各种初始化方法来避免这些问题，如：通过保持一层网络的输入和输出方差不变来防止梯度消失的Xavier 初始化方法；He 初始化方法通过加重权重方差的方式弥补ReLU 激活函数［18］1/2 为零的状态。

目前针对权重初始化方法的思路更多偏向于正态分布和均匀分布，但还不能更好地以合适的数据对深度学习网络进行初始化。若使模型的初始权重分布与训练后模型权重的分布接近，将有助于模型获得最优解，减少模型的训练时间。因此，寻找一个更合适的数学分布规律来进行权重初始化，是本文探讨并验证的核心问题。

1.2 权重初始化方法

网络模型的训练实质就是更新权值并找到最优权值的过程。预训练模型的权值就是网络训练最终找到的最优权值，若可以从预训练模型的权值中总结出规律，研究并制定一种权重初始化的方法，有助于提升网络模型的训练速度和最终精确度。

针对权重初始化目前存在的问题，本文提出一种有效的权重初始化方法，具体解决思路如下：1）从预训练模型的权值入手，查看并分析预训练模型的权值分布规律；2）通过分析预训练模型的权值分布特征，发现权重分布具有幂律分布特征，进一步进行幂律分布拟合的检验实验，考虑制定一种以幂律分布为基础的权重初始化方法；3）优化数据分布结构，制定标准化的对称幂律分布数据，即本文提出的NSPL 初始化方法。

本文从预训练模型的权重入手，查看并分析预训练模型的权重分布规律，探究幂律分布在权重初始化中的作用。对比实验结果表明，本文提出的方法有助于减少网络权重的训练时间，具有提升网络最终精确度的能力。

1.3 预训练模型的权重分布分析

本节使用的是Pytorch 框架下torchvision 中的预训练模型，它是基于ImageNet 数据集上训练出来的，通过查看预训练模型的权值，对预训练模型权值做相关统计分布分析。依据幂律分布的判断性质，在双对数坐标下，幂律分布表现为一条斜率幂指数为负数的直线，这一线性关系是判断给定的实例中随机变量是否满足幂律的依据。本文对AlexNet 和ResNet18 预训练模型的所有卷积层权重进行双对数线性拟合，并计算其拟合优度R2。

首先针对AlexNet［19］网络的卷积层权值分布进行处理。依次读取AlexNet预训练模型的权重参数，并使用概率分布来可视化权值的分布情况。该网络的五层卷积层权值数据的概率分布情况如图1 所示，其预训练模型权重的双对数拟合图如图2 所示。根据AlexNet预训练模型的权值分布情况，可以通过其高峰、长尾的特点，进一步对更深层的ResNet18［20］预训练模型进行相同的实验。其中，ResNet18 共有17 层（加上输入层）卷积层，其权值概率密度分布情况如图3 所示，其预训练模型权重的双对数拟合图如图4 所示。

高潮立马掏出手机，调出“诗的妾”那条在去温州的列车上发来的短信，一看时间，19:47/23/07/2011，一下子惊呆了！高潮知道，那桩举世闻名的动车交通事故，发生在几天前的七月二十三日晚间。高潮顾不得许多了，立马破戒，拨打“诗的妾”的手机，他听到的是一个彬彬有礼而缺少温度的声音：您拨打的电话已关机，请稍后再拨……

从图1 和图3 可以看出，这两个网络的预训练模型权值数据皆具有高峰、长尾的特点。在各种数学分布中，同样具有该特点的是幂律分布，推断预训练模型的权重分布单侧倾向幂律分布。从图2 和图4中的双对数线性拟合结果可以看出，所有层权重线性拟合优度R2值都是在0.8 左右，可以得出预训练网络模型的权重分布并不完全为幂律分布，属于指数截断的幂律分布［21］。从数据上来看，实际分布中权值接近于0 的数据少于幂律分布，但根据对深度网络模型正则化［22］研究结果，在损失函数中加入L1 或L2 正则化项［23］，将使模型中更多的权值为0 或者接近于0，且模型的泛化能力更强。基于此，本文以幂律分布来初始化网络，而没有采用指数截断的幂律分布。本文制定一种标准化的对称幂律分布的权重初始化方法，用来确定幂律分布在权值中的作用。

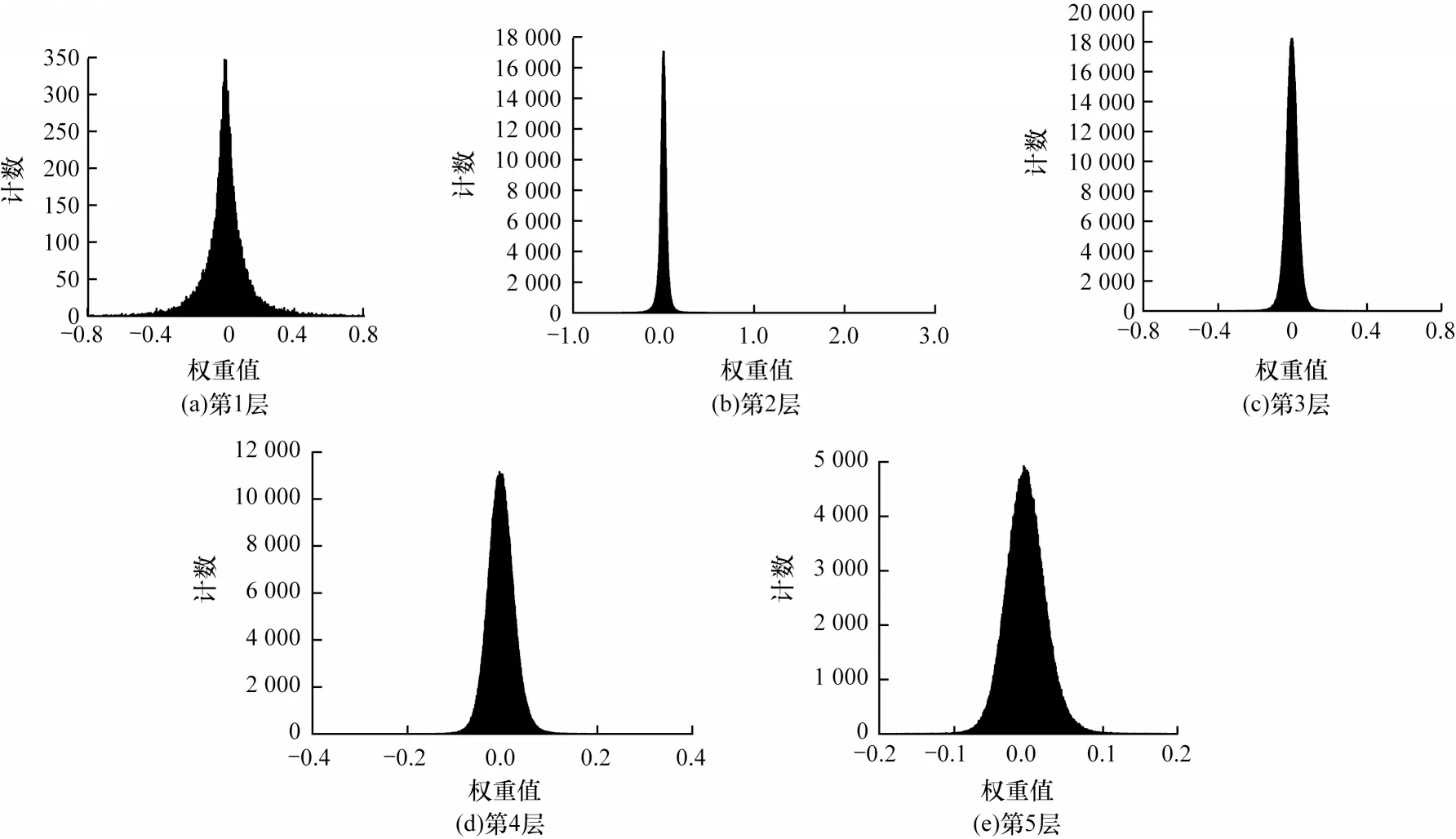
图1 AlexNet 预训练模型权重数据概率分布Fig.1 Probability distribution of weight data of AlexNet pre-training model

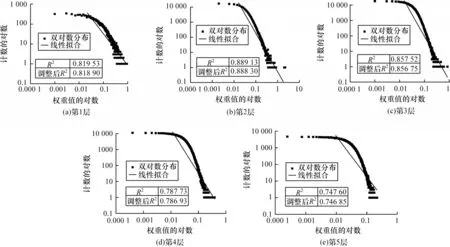
图2 AlexNet 预训练模型权重的双对数拟合图Fig.2 Double log-fitting diagram of AlexNet pre-training model weight

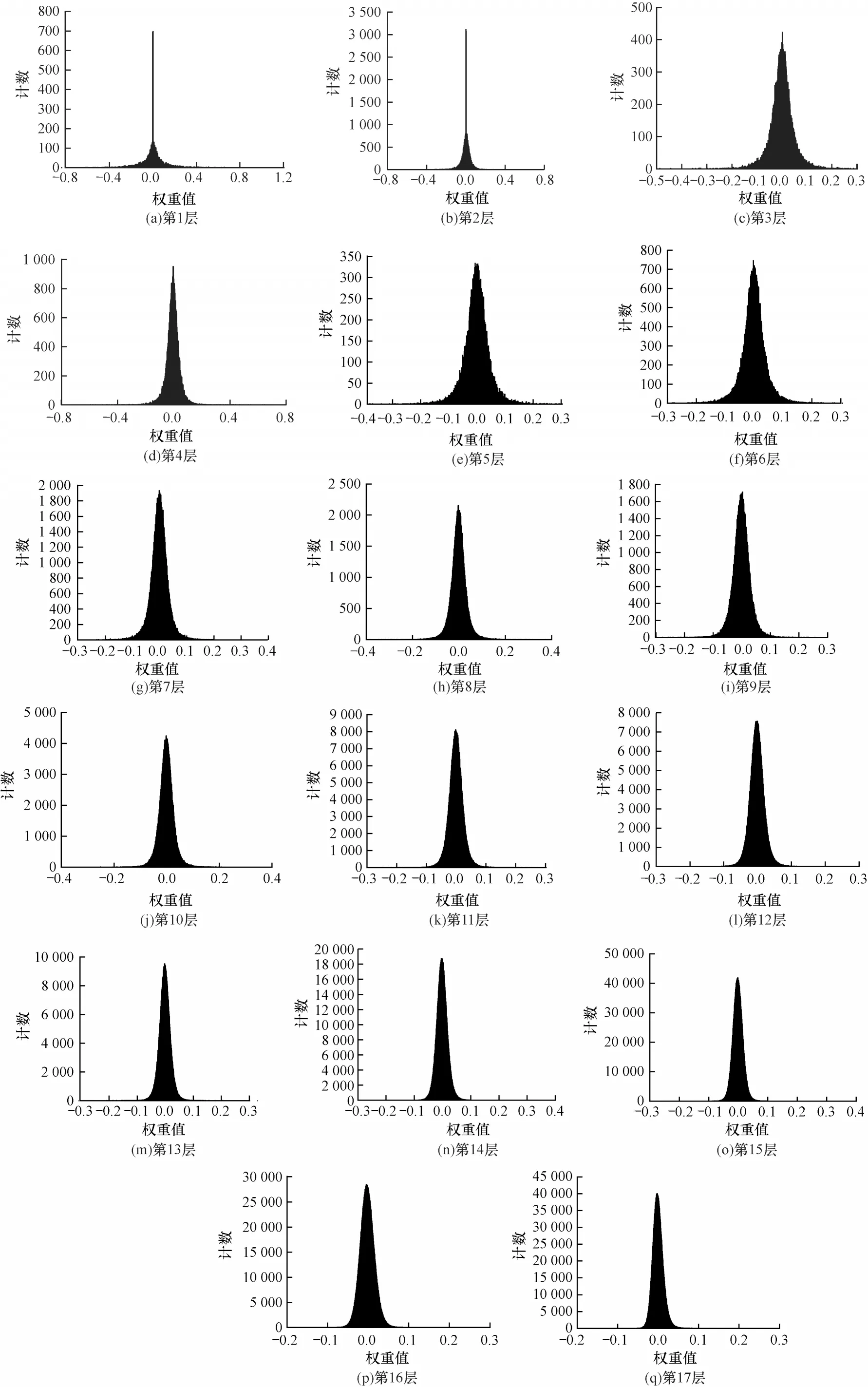
图3 ResNet18 预训练模型权重数据概率分布Fig.3 Probability distribution of weight data of ResNet18 pre-training model

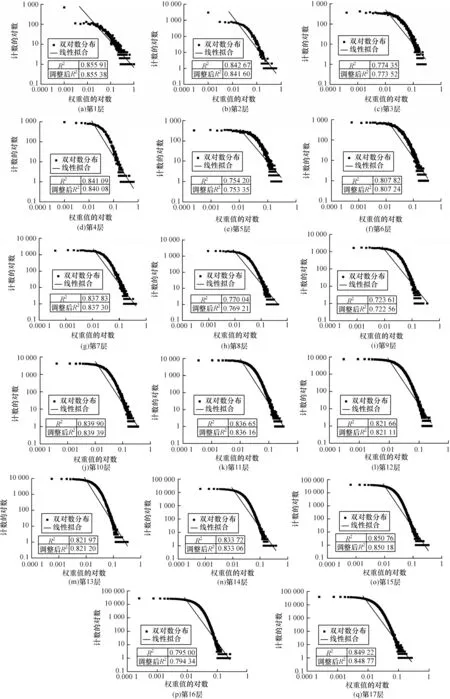
图4 ResNet18 预训练模型权重的双对数拟合图Fig.4 Doublelog-fitting diagram of ResNet18 pre-training model weight

2 标准化对称幂律分布

2.1 函数形式的数学推导

归一化的对称幂律函数推导过程如下：

1）幂律分布的公式为：

2）标准化过程，令：

通过计算得：

将c代入式（1）得：

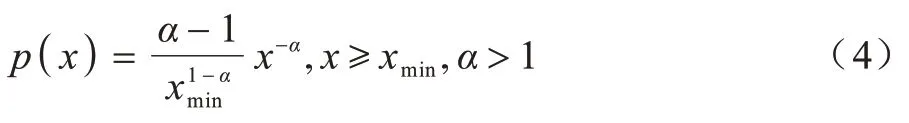
式（4）即为单侧标准化的幂律分布函数公式。

标准化对称幂律函数为：

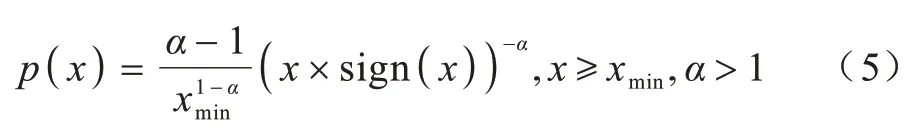
2.2 权值数据的生成算法

本节算法致力于生成指定数量的标准化对称幂律数据，用来初始化不同网络模型，具体步骤如下：

清翁方纲亦在其《石洲诗话》中云：“马戴五律……直可与盛唐诸贤侪伍，不当以晚唐论矣。”[13]如其《宿翠微寺》“积翠含微月，遥泉韵细风”[5]，《夜下湘中》“露洗寒山遍，波摇楚月空”[5]，其中“微月”妙，承“含”极妙。明杨慎评曰：“‘积霭沉斜月，孤灯照落泉’，喻凫诗也。‘积翠含微月，遥泉韵细风’，马戴诗也。二诗幽思同而句法亦相似。”[14]“含、韵、洗、摇”等动词的使用含蓄蕴藉，自然融洽，浑然天成，以动词巧妙连缀意象，还有如：“余霞媚秋汉，迥月濯沧波”(《秋郊夕望》)[5]、“微红拂秋汉，片白透长波”(《落照》)[5]、“霓虹侵栈道，风雨杂江声”(《送人游蜀》)[5]颇有盛唐之气象。

现代建筑在设计时除保证建筑的安全性、舒适度、智能化和生态环境因素外，还应注重能源的有效使用和节约，减小外围护结构的传热系数，强化建筑外围护结构的隔热构造。

步骤2将标准化的幂律函数做对称，得到标准化的对称幂律函数。

步骤3分别计算网络模型中各个卷积层的参数数量。

步骤4运用本文算法得到对应数量的参数值，分别对网络的卷积层权值重新初始化。生成的权值应当符合分布要求，并且无大量、连续的相同数据。

1）对称幂律函数的生成算法

手机端也能查看控制系统发送来的数据，在手机上使用应用程序读取数据并转化成数据曲线，使数据可视化程度提高.在20 m范围内可通过手机对机器人主体机身系统或机械臂进行控制，增加了人机互动性.

依据算法设计，算法1 可以得到标准化的对称幂律分布函数。

算法1标准化的对称幂律函数

通过实验分别对比同一个网络下不同初始化方法的初始精确度和最终模型精确度的差异，最终得出本文提出的NSPL 初始化可以有效提高模型的训练速度和最终精确度。

2）对称幂律数据生成

步骤1根据幂律分布的公式，推导出标准化的幂律函数（见2.1 节）。

在算法1 建立了标准化的对称幂律分布函数后，根据计算出的网络模型每一层的权重参数量，使用算法2 来生成对称幂律数据。

算法2对称幂律数据生成算法

3 实验结果与分析

为验证本文提出的NSPL 初始化方法有助于缩短网络训练时间，提高网络的最终精确度，设置以下的对比实验：运用cifar10 数据集分别在AlexNet 网络和ResNet-32 网络上进行训练，而在训练过程中每一个网络都将使用3 种权重初始化方法进行初始化，分别为He 的均匀分布初始化、He 的正态分布初始化［16］和NSPL 初始化。

双及物构式(双宾构式)是指在句法层面的动词能同时携带间接宾语和直接宾语的语言形式，其结构可以码化为［NSVN1N2］。双及物构式的基本意义可以表述为“客体实际的、成功的转移”，也就是“客体从初始领有者被传递给最终领有者的过程”。这就要求进入双及物构式的动词必须具有“给予”义，必须能支配三个名词性成分，动词后的“N1”应该是有生命的。但是我们发现，许多非“给予”类、非“三价”动词也能进入双及物构式；处于“N1”位置上的名词也并非都是有生命的，这其中一定有什么因素在起作用，本小节就拟探讨这个问题。

本文两组实验的流程设计如下：

1）获取数据集，设置网络模型；

2）计算并记录每一层网络模型参数量；

3）利用算法1 制作出标准化的对称幂律分布函数；

4）利用算法2 生成与网络模型参数量对应大小的对称幂律数据；

5）使用3 种不同的权重初始化方法对网络模型的参数进行初始化；

2）ResNet32 网络各层权重数量

7）每一轮训练集结束后，使用验证集进行准确率验证，并记录该准确率。

笔者采用线上、线下相结合的混合式教学模式：首先开始上课时，我们对线上内容进行测验或课前问题答案展示，这样做可以监督学生线上自觉进行微课视频的学习，增强了同学们的成就感和满足感，激发了同学们学习编程的兴趣和自信心，同时也给学生提供了锻炼自我的机会。

3.1 卷积层参数量计算

卷积层权重参数量的计算公式为：

其中：in_channels 表示输入的通道数；out_channels表示输出的通道数；kernel_size 表示卷积核的大小。

1）AlexNet 网络各层权重数量

很明显，在理论上而言，大题难度对试卷难度的影响由其所占的比重决定.第三大题总分为70分，对试卷难度的影响也最大.第三大题的难度提高0.1，整个试卷的难度将会增加0.04667.相应地，提高0.1个单位的第二大题的难度，整个试卷的难度只会增加0.0133.通过这个线性关系式，我们可以定量地描述题目难度与试卷难度之间的线性关系，由此推断解答题在全卷难度稳定中发挥的作用最大.

结合式（6）计算AlexNet 网络所有卷积层的权重数量，如表1 所示。

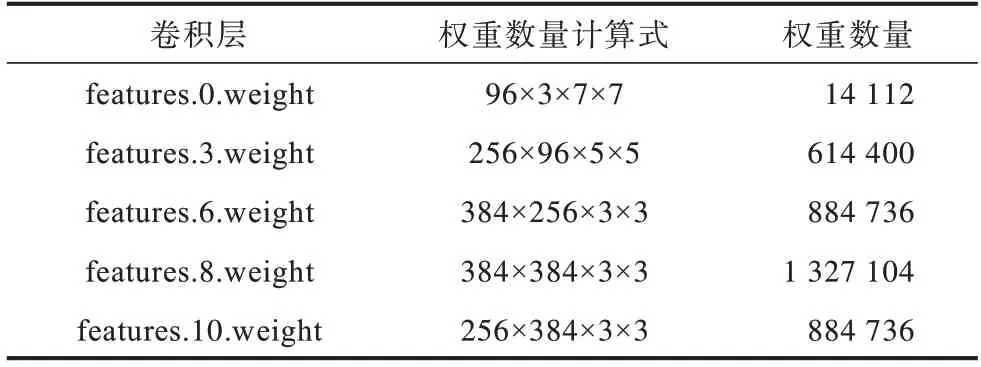
表1 AlexNet 网络各层权重数量Table 1 Weight quantity of each layer of AlexNet network

6）使用训练集进行训练，学习权重参数；

ResNet32 网络是以block 块为基本单位组成的网络结构，因此在此处以不同的block 来对不同的卷积层的情况进行描述。结合式（6）计算该网络卷积层种类以及对应的权重参数量，如表2 所示。

表2 ResNet-32 网络各层权重数量Table 2 Weight quantity of each layer of ResNet-32 network

3.2 网络初始权重分布情况

下文所有权重数据与ResNet32 网络相似，此处仅以AelxNet 为示例。

1）NSPL 初始化数据。使用本文提出的算法结合AlexNet 的五层卷积层所需要的权重参数量，生成NSPL 初始化数据。本文算法生成的权重初始化数据分布如图5 所示。从图5 可以看出，该数据充分展现了幂律分布的高峰、长尾现象。因为是标准化的对称幂律分布，所以高峰和长尾特征比较明显。

随着经济建设的高速发展，我国已经进入高铁、扫码支付、共享单车和网购新四大发明时代，信息化已经成为这个时代的明显特征。这个时代的学生具有明显的信息化特征，以智能手机为代表的智能终端几乎人手一台。在这个背景下，通过变革传统课堂教师讲、学生听的授课方式，用信息化教学的理念，对课程体系进行重建势在必行。

图5 对称幂律初始化数据分布Fig.5 Distribution of symmetric power law initialization data

本文实验是对比使用不同权重初始化的网络训练首轮次训练后的测试集精确度及后续网络模型的收敛速度。通过对比同一训练轮次下的不同初始化方法达到的精确度，得出其中一个初始化方法更有助于提升网络训练速度和最终模型准确率的结论。

H公司的财务人员、销售人员、行政人员基本是大专学历以下，而应收账款管理需要很强的专业性，他们又有本职工作需要投入大量精力，因而很难将应收账款管理工作做好。因此，员工素质不高也是H公司应收账款持续增多、坏账增加原因之一。

图6 He 方法的正态分布初始化数据分布Fig.6 Distribution of normal distribution initialization data of He method

3）He 的均匀分布初始化数据。使用He 均匀分布初始化方法对网络权重进行初始化，读取网络初始权值，也就是该初始化方法生成的数据，该权重初始化方法的数据分布如图7 所示。该初始化方法是Pytorch1.7 中默认的初始化方法，当网络不指定初始化方法时，会调用该方法对卷积层进行初始化。

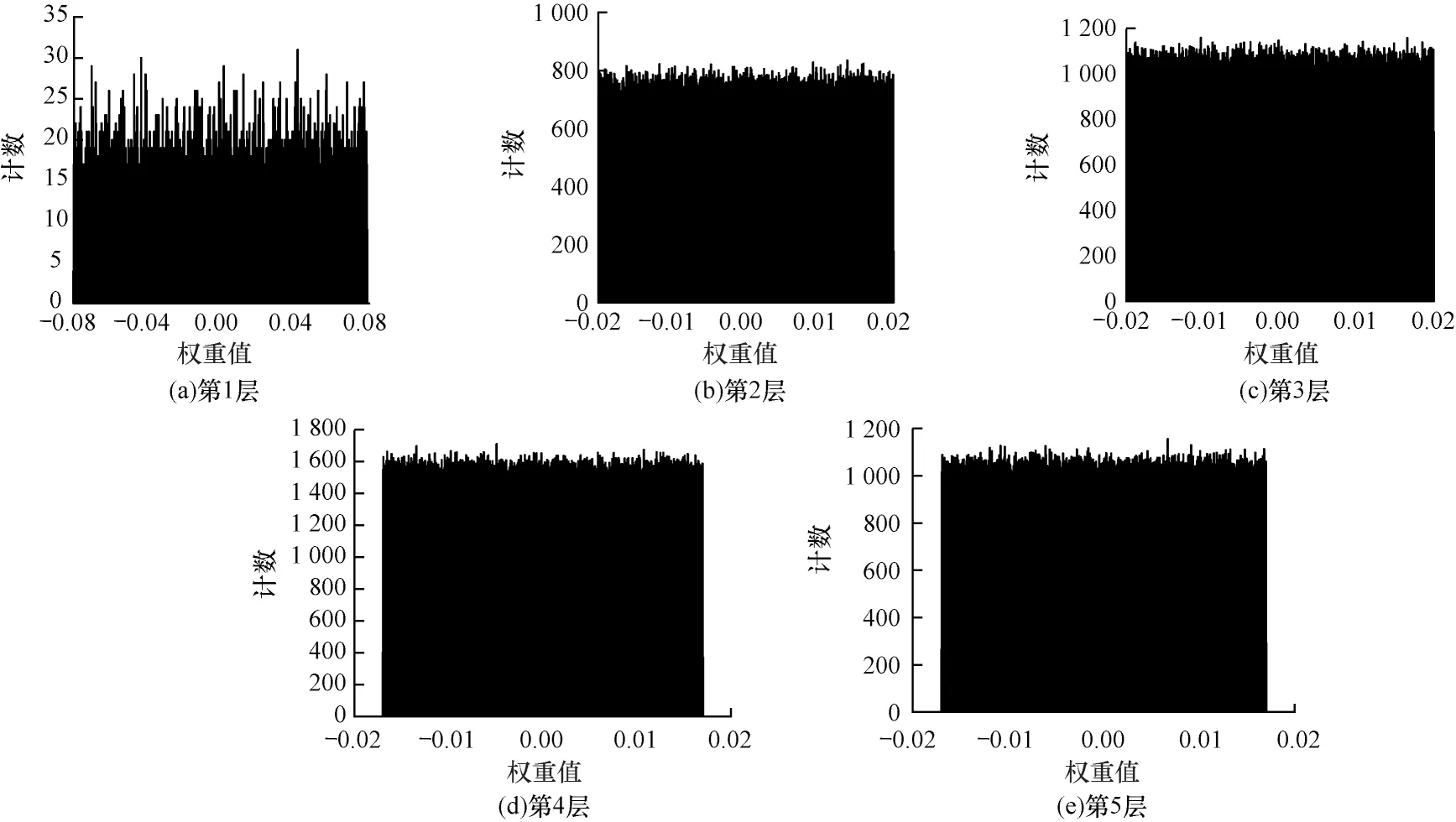
图7 He 方法的均匀分布初始化数据分布Fig.7 Distribution of uniformly distributed initialization data for He method

3.3 对比实验

对比实验过程如下：

1）实验设计

本文实验使用cifar-10 数据集，在AlexNet 网络和ResNet32 网络上进行实验，将NSPL 初始化的实验结果与He 的正态分布初始化、均匀分布初始化方法的实验结果进行对比分析。

cifar10 数据集是一个更接近现实物品的RGB彩色图像，包含10 个类别，每个类别有6 000 个图像，分别为50 000 张训练图片和10 000 张测试图片。本文实验在训练集上进行模型训练，使用测试集进行测试，以对比测试集的准确度。

2）He 方法的正态分布初始化数据。使用He 正态分布初始化方法对网络权重进行初始化，读取网络初始权值，将其数据分布可视化，如图6 所示。该方法的权值数据分布就是非常典型的正态分布钟形图像，依据该方法对方差的计算和控制可以看出每一层数据分布情况的不同。

实际线路长度大于 10 km 时，可将整个线路分割为多个 10 km 的小线路段，即在式(4)中增加线路数，同时将该条线路中几个点看作是故障点进行计算[24]。

2）实验过程

针对AlexNet 网络和ResNet32 网络，分别使用上文中提到的3 种方法进行权重初始化。网络每一轮次训练结束都用验证集测试当前网络的准确度并进行记录，将3 种精确度对应的所有轮次的验证集精确度进行对比分析。（1）在AlexNet 网络实验过程中，使用的超参数设置如下：随机梯度下降法（Stochastic Gradient Descent，SGD）优化器，动量momentum=0.9，批尺寸batch_size=64，学习率lr=0.015，测试尺寸test_batch=1 000，训练轮次epochs=30，损失函数使用CrossEntropyLoss。

为推动全球耕地建设保护、生态文明建设及农业可持续发展，奥特奇作物科学中国区业务经理马卫民表示，赛土丰科研团队经过长期的研究与实验，对微生物进行规模化培养，筛选代谢提取物，用于激活土壤中有益的微生物，解决土壤因缺乏微生物带来的土传病害等诸多问题，进一步促进作物根系发展，以期实现农民增产增收。

图8 所示为3 种不同权重初始化方法在AlexNet网络上各个轮次的训练精确度。

随着互联网信息技术和智能电子设备的不断发展，微课作为一个新的教学产物出现在了我国的教育计划中。微课主要指视频内容在十分钟之内的一种教学方式，在简短的视频中要集中重点语文知识和其他相关的拓展内容，通过调查我们发现，微课的教学效率是非常高的，微课凭借简短而精练的内容深深吸引了学生的注意力。虽然微课不能浓缩一节课的全部内容，但是通过板块化教学，使得微课将一个个重点知识变得生动有趣，学生理解起来也非常容易。在信息技术快速发展的时代背景下，微课作为移动教学的一种方式，既满足了不同学习能力学生的学习要求，还达到了教育部要求的深度教学。

图8 AlexNet 训练精确度对比Fig.8 Comparison of AlexNet training accuracy

在AlexNet 网络的对比实验中，通过图8 可以看出NSPL 初始化方法和He 正态分布初始化的初始轮次精确度优于He 均匀分布初始化，NSPL 初始化方法相较于He 的均匀分布和正态分布初始化方法的最终精确度也有微弱的提升。本文实验进一步使用了具有更高复杂度的ResNet32 网络模型来验证NSPL 初始化的使用效果。（2）在ResNet32 网络实验过程中，使用的超参数设置如下：SGD 优化器，动量momentum=0.9，批尺寸batch_size=128，学习率为lr=0.01，测试尺寸test_epochs=100，训练轮次epochs=30，损失函数使用CrossEntropyLoss。

图9 所示为3 种不同权重初始化方法在ResNet32 网络上各个轮次的训练精确度对比，通过图9 可以看出，在模型精确度提升的过程中，NSPL初始化有助于优化网络的训练过程，加快收敛速度。

图9 ResNet32 训练精确度对比Fig.9 Comparison of ResNet32 training accuracy

3.4 对比实验分析

通过图8 实验结果对比可以发现，He 的正态分布初始化方法和本文提出的NSPL 始化方法在初始轮次中有较高的准确度。在最终模型趋于稳定时，NSPL 初始化的精确度比He 的正态分布初始化方法提高3%。总地来说，NSPL 初始化在AlexNet 网络上具有优化网络模型训练过程的优点。

通过图9 实验结果对比可以发现，在更为复杂的ResNet32 网络中，NSPL 初始化方法在首轮次中的精确度比He 初始化方法的精确度提高60%，并且模型收敛的速度更快，其最终精确度比He 初始化方法提高8%。在更深层的网络中，NSPL 初始化方法具有更优秀的表现。

师:同学们，这节课老师和大家一起复习了相似的性质、判定和应用，在复习过程中我们梳理了知识，小结方法，提炼了策略，这三者合起来就形成我们的解题能力．当然能力永远是第二位的，那么第一位是什么呢？那是“意识”，就是我们要“想到用”相似来解题，“意识”让我们“想到用”，能力让我们“会用”，如何才能“用好”“用巧”？这就要求我们站在一定的高度，掌握一定的数学思想，关于这一点我们同学也许不太理解．下面我来解决这个问题，同学们“今天这节课老师主要和大家探讨了几个题目？”

通过上述两组对比实验可以发现，NSPL 初始化方法有助于提升网络训练的速度和最终准确度，说明幂律分布也可以作为一种权重初始化的模型方法。

4 结束语

本文通过理论推导和实验验证，提出一种提升网络模型训练速度和精确度的权重初始化方法——对称幂律（NSPL）初始化方法。同时，设置2 种网络结构，在3 种不同权重初始化下进行对比实验，使用cifar10 数据集分别训练，对比每一轮次的模型训练精确度。实验结果表明，本文NSPL 初始化方法能够优化网络训练过程，加快收敛速度。本文采用的是标准化后的对称幂律数据，并没有深入研究截断幂律分布拟合的情况，下一步将统计并分析大量预训练模型的权重参数分布情况，结合不同网络模型的层数及不同数据集等影响权重初始化的因素，制定出更有针对性的基于幂律分布的初始化方法。