一种高效的跨平台工作流优化方法

杜清华，张凯

（1.复旦大学 软件学院，上海 200438；2.复旦大学 计算机科学技术学院，上海 200438）

0 概述

为了满足数据科学的多种需求，具有扩展性的跨平台数据分析系统不断涌现，如Rheem［1］、Musketeer［2］等。这类系统将Java、Spark［3］等不同数据处理平台作为底层实现，为用户抽象出一套数据分析接口，帮助用户更加简单地完成对复杂数据分析任务的计算。数据分析任务在跨平台系统中将以工作流为载体进行计算，工作流主要存在逻辑工作流和物理工作流两种形式。用户通过接口编写逻辑工作流，然后系统需要为逻辑工作流中的每个算子选择相应的物理实现而形成可执行的物理工作流。逻辑算子的平台选择对于工作流整体性能至关重要，因为算子在不同平台上的实现会存在性能间的显著差异，这也是针对跨平台工作流进行优化的主要方式之一。

目前，部分研究人员［4-5］针对跨平台工作流采用了基于成本的优化方法，利用函数公式对影响算子运行成本的因素进行建模，从而获得可以估计某个算子具体运行时间的成本模型［6］。然而，将传统成本优化方法应用于跨平台工作流时会存在两个问题：首先，成本模型普遍具有一个固定的函数形式，例如Rheemix［7］中所使用的线性函数式成本模型，由于线性表达式本身具有难以表达复杂或非线性关系的特点，导致其不能很好地反映各因素对不同平台、不同计算类型算子运行时间成本的影响程度；其次，它需要系统管理员做大量工作来调优函数式成本模型的参数。尤其在跨平台系统中这个问题会更加严重，因为跨平台系统的算子数量会数倍于传统数据处理平台［1］，这将使得函数模型的参数数量很容易达到数百条，手工调整它们不仅具有挑战性而且非常耗时［8］。

随着机器学习的发展，一些工作开始探索使用新的方式来实现跨平台工作流优化。Robopt［9］使用随机森林算法作为成本模型，虽然该算法的鲁棒性较好，但是无法捕捉工作流中所隐含的信息，如工作流的结构信息和算子的运行时序信息等。由于不同的算子具有不同的属性（如参数、子节点），这使得物理工作流具有独特的结构信息。虽然部分研究［10-12］在成本估计上探索了结构信息并取得了不错的效果，但他们的目标仅适用于单平台查询优化，如数据库查询优化等。文献［13-15］提出使用基于成本的强化学习优化方法，该方法虽然可以降低优化器的维护成本，但是十分依赖模型的设计及训练数据，且启发式方法所固有的不稳定性将在某些情况下导致优化效果并不明显。

为了提升跨平台工作流的执行性能，本文提出一种GGFN（GAT-BiGRU-FC Network）模型作为成本模型，用于实现高效的跨平台工作流优化。基于图注意力机制和循环网络门控机制，GGFN 模型可以在具有有向无环图（Directed Acyclic Graph，DAG）结构的跨平台工作流上挖掘结构信息和记忆算子的运行时序信息，该模型以算子特征和工作流特征作为输入，从而对跨平台工作流实现更准确的成本估计。在此基础上，通过对逻辑算子的实现平台进行枚举，并选择其中运行时间成本低的物理工作流作为最终的优化结果。同时，为加速枚举过程，本文设计延迟贪婪剪枝方法以降低优化时间的开销。

1 背景及相关工作

1.1 跨平台工作流优化

工作流优化是数据处理平台用于提升性能的主要方式，优化通过将逻辑工作流转换为运行成本更低的可执行物理工作流，从而加快数据处理任务的运行速度。基于成本的优化方法［16］是传统工作流优化中最常用的方法之一，而成本模型是实现基于成本优化的基础。例如，KeystoneML［17］在进行工作流优化时，依据资源使用情况、输入输出基数以及算子信息等给出相应的函数公式作为成本模型。文献［18］使用循环神经网络作为成本模型来预测数据库查询计划的运行成本。文献［19］提出为工作流中的表达式创建多个机器学习模型并以此实现准确度更好、覆盖率更高的成本估计。

然而，跨平台系统在跨平台工作流优化方面并没有像数据库或其他数据处理平台一样拥有成熟且可靠的优化方法。例如，文献［20］虽然介绍了跨平台系统相关工作，但并未针对其工作流提供优化方法，BigDAWG［21］为跨平台工作流所提供的优化方式需要用户通过Scope 和Cast 命令指定运行工作流的具体平台。这种优化方式不仅存在优化效果的不确定性，而且增加了用户的工作量和难度。此外，LaraDB［22］和Myria［8］通过利用已有经验所制定的规则实现优化，但是过度耦合的优化规则会给系统的扩展性带来困难。因此，基于成本的优化方法仍然是研究人员进行跨平台工作流优化所使用的主要方式。例如，Rheemix［7］为其系统中每个算子定义了成本的计算过程，但是由于跨平台系统中算子数量大、计算类型多，因此将这种函数式的成本模型应用于跨平台优化很容易出现参数规模达到数百而产生参数调优困难的问题。Musketeer［2］通过对每个算子成本进行累加的方式计算工作流整体成本，然而这种方式会忽略不同平台算子间的数据传输所带来的时间成本。虽然Robopt［9］使用了机器学习算法来避免繁琐的参数调优工作，但是其成本模型由于扩展性不足且无法捕捉工作流的潜在信息，而不能实现更好的优化效果。

1.2 图注意力网络与门控循环单元

图注意力网络（Graph Attention Network，GAT）是由PETAR等［23］所提出的用于处理图结构数据的神经网络模型。GAT 可以通过堆叠应用注意力机制的网络层来获取图上每个节点的邻域特征，并为邻域中的不同节点分配不同的权重作为注意力系数。这使得可以在不需要高成本的矩阵运算和预先知道图结构信息的情况下实现高效的图信息处理。通过这种方式，GAT 可以解决基于频域的图处理方法所无法解决的动态图问题，如图卷积网络（Graph Convolutional Network，GCN）［24］，同时也能应用于图的归纳学习和直推学习。需要注意的是，由于GAT网络是对图顶点进行逐个运算，每次计算都需要对图上所有顶点进行循环遍历，这意味着GAT 可以摆脱传统图结构处理中的Laplacian 矩阵的束缚并实现对有向图的处理。

门控循环单元（Gate Recurrent Unit，GRU）是由CHO等［25］提出用于解决长期记忆和反向传播中的梯度等问题的网络模型，与长短期记忆（Long Short-Term Memory，LSTM）同为循环神经网络（Recurrent Neural Network，RNN）的变体。LSTM 的门控机制被广泛应用于分析并捕获时间序列数据中的长期依赖关系。GRU 在LSTM 的基础上通过优化门结构而保证了对于序列数据的长期记忆效果。在大量的实验数据中证明，GRU 在模型准确度方面与LSTM 有着相似的效果，但由于GRU 的门控数少于LSTM，在模型训练中将会有更少的参数需要计算，因此GRU的模型收敛速度会更快。

2 相关概念及问题定义

逻辑工作流是由用户根据任务需求所创建而形成的DAG 型结构的有向数据流图。其顶点是逻辑算子，表示对数据进行分析处理的任务逻辑且与平台无关，边代表算子之间的数据流。逻辑工作流用符号可以表示为lw={O,E}。其中，O={o1,o2,…,on}表示逻辑算子集合，oi表示第i个逻辑算子，n表示逻辑算子的数量，E={e1,e2,…,em}表示数据流边集合，ek=[oi,oj]表示算子间的数据流边。

定义1（跨平台工作流优化）针对跨平台工作流，给定一个优化转换操作Opt=Min{pltSec(∙)}，实现将逻辑工作流lw 转化为最优物理工作流pwmin。在由平台选择操作pltSec（lw）所生成的物理工作流集合PW 中存在pwj∊PW，使得对于任意的pwi∊PW，pwi≠pwj，满 足cost(pwj)≤cost(pwi)。此 时，pwmin=pwj=Opt(lw)为跨平台工作流优化的目标结果。

3 基于GGFN 模型的跨平台工作流优化

3.1 方法概述

为了提升跨平台工作流的执行性能并克服已有优化工作中的问题，本文提出一种基于GGFN 模型的跨平台工作流优化方法，该方法的整体优化框架如图1 所示。

图1 基于GGFN 模型的跨平台工作流优化框架Fig.1 Cross-platform workflow optimization framework based on GGFN model

首先对于用户输入的逻辑工作流进行向量化操作，从而避免后续每次进行成本估计时向量转换所带来的优化开销。接着对每个逻辑算子进行算子实现平台的枚举，同时利用延迟贪婪剪枝方法以加速枚举过程。枚举算法将使用基于图注意力网络和门控循环单元所形成的GGFN 模型对跨平台工作流所做出的成本估计结果为依据进行平台选择。最后成本最低的物理工作流向量将会被选择出来，并将其反向量化为可执行的物理工作流后进行部署和执行。与此同时，物理工作流的执行过程会将被记录并进行日志分析，以此来作为后续GGFN 模型的线下训练数据。

3.2 GGFN 模型

对物理工作流进行准确的成本估计是本文实现高效跨平台工作流优化的重要基础。在总结了已有工作的不足之处后，本文提出了基于图注意力神经网络（GAT）与门控循环单元（GRU）的GGFN 成本模型，其结构如图2 所示。该模型包含两个输入部分，一是算子特征，二是工作流特征。算子特征将经过图注意力网络的处理来捕捉工作流的整体结构信息以及各个算子之间的交互关系。双向门控循环单元将对算子之间的运行时序关系进行挖掘并获得相应的运行状态信息，其编码结果将与工作流特征进行融合。融合后的特征将被输入到3 层全连接层进行工作流运行时间成本的预测，并在输出层得到预测结果。

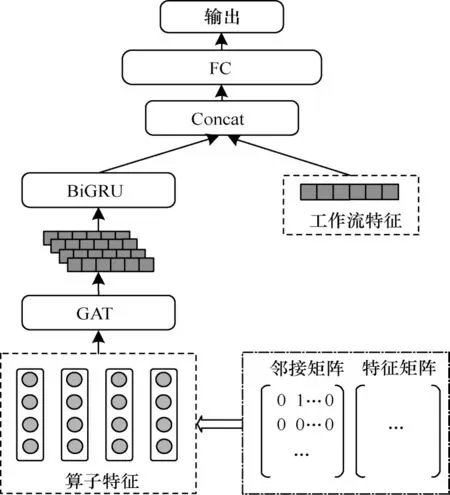
图2 基于GAT 和BiGRU 的GGFN 模型架构Fig.2 The GGFN model architecture based on GAT and BiGRU

3.2.1 输入特征

GGFN 模型的输入特征被设计为以下2 个部分：

1）工作流特征。工作流的整体信息表示以及输入数据集信息，包括算子数量、平台数量、结构信息、输入数据集大小、输入数据集分布、输入平均元组大小等。

2）算子特征。工作流中每个算子的信息表示，包括算子并行度、父节点数量、子节点数量、用户自定义函数（User Defined Function，UDF）复杂度、计算分析类型、输入输出基数、算子运行平台等。

其中，算子特征结合邻接矩阵来表示跨平台工作流的DAG 结构，从而可以更好地帮助GGFN 模型挖掘工作流结构信息和算子的运行时序信息。该设计满足特征的扩展性要求，当在跨平台系统中添加新的平台或算子时，只需进行相应特征位的映射范围扩展。

3.2.2 图注意力网络

由于GAT 中的注意力机制可以为每个邻居节点分配不同的注意力系数，因此可以识别出相对于当前节点更重要的邻居节点。在跨平台工作流中，不同算子对相邻算子的影响程度是不同的。例如，Fliter 算子会通过减少数据量而对下一个邻居算子的数据处理时间产生较大影响，而Sort 算子对后续邻居算子的影响将取决于该邻居算子对数据顺序的依赖性。此外，由于跨平台工作流为DAG 图结构，图网络模型将可以更好地实现对工作流结构信息的捕捉。因此，本文在GGFN 模型中引入图注意力网络（GAT）来实现对工作流整体结构信息和算子间关系信息的特征提取。

GAT 的计算主要包括两步，首先是计算注意力系数，计算过程如式（1）、式（2）所示：

其中：W为共享参数对顶点特征进行增维；[∙||∙]表示对节点i和j变换后的特征进行拼接操作；a(∙)表示将拼接后的高位特征映射到一个实数上。式（1）用于计算节点i和其邻居（j∊Ni）间的相似系数；式（2）通过LeakyReLU(∙)进行归一化操作得到节点i和j的注意力系数αij。

然后需要根据计算好的注意力系数进行特征的加权求和。为了加强GAT 模型在学习过程中的稳定性，本文引入了多头注意力机制来获得多个注意力系数关系，如图3 所示。

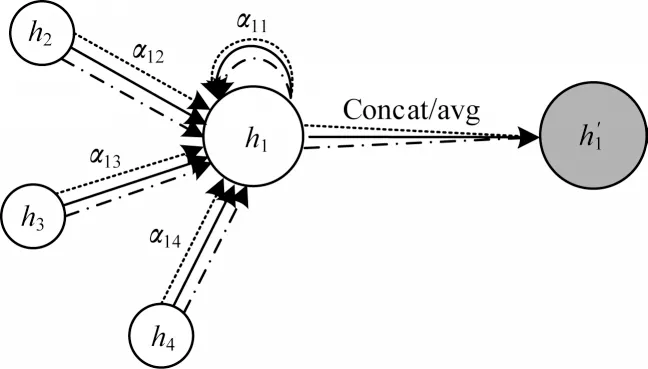
图3 GAT 中的多头注意力机制Fig.3 Multi-head attention mechanism in GAT

图3 所示为在K个注意力机制下（K=3）算子节点的更新状态。通过利用多头注意力机制计算节点新特征的计算公式如式（3）所示：

3.2.3 门控循环单元

跨平台工作流以算子顺序执行，运行时间包括从源算子到所有算子执行完成的最终状态，因此需要考虑前序执行算子的计算时间及计算状态语义。基于上述情况，可以利用循环神经网络（RNN）对序列数据的记忆效果来获取跨平台工作流中算子执行顺序对最终状态的影响。而门控循环单元（GRU）作为循环神经网络的一种特殊形式，利用其门控机制可以很好地实现长期记忆并避免RNN 中梯度消失和梯度爆炸的问题。本文GGFN 模型中的GRU 用于记忆算子结构和运行的时序信息，并对其特征进行编码。GRU 的单元结构如图4 所示。

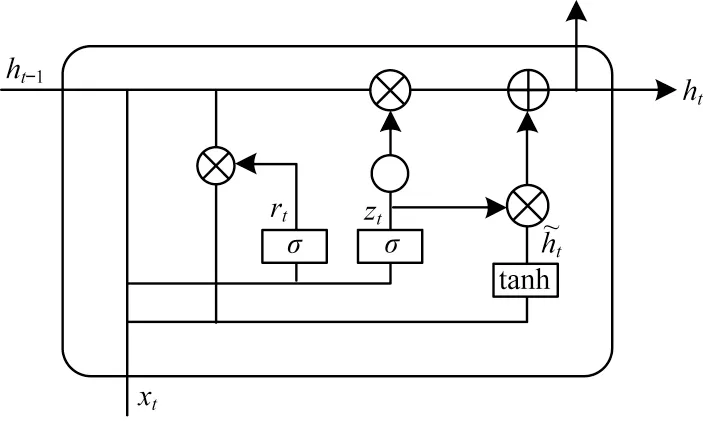
图4 GRU 单元结构Fig.4 The unit structure of GRU

在图4 中，rt为重置门，用于控制前一时刻隐层单元对当前输入的影响，有助于捕获运行序列中的短期依赖关系，zt为更新门，用于控制过去信息的保留和传递情况，有助于捕获物理算子运行时间序列中的长期依赖关系。在t时刻，GRU 的计算过程如式（4）～式（7）所示：

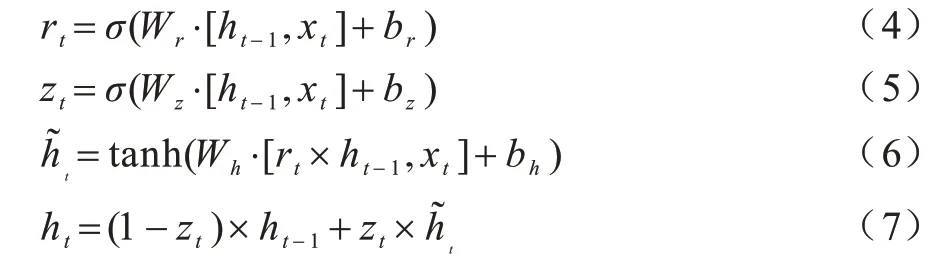
其中：xt为t时刻的输入；W表示权重参数；b表示偏差向量；ht-1、ht分别表示t−1和t时刻的候选隐 藏层状态。

在跨平台工作流中，不同的算子实现需要在不同平台中运行，因此后续算子的实现平台对当前平台算子的数据输出格式及数据传输是存在时间成本影响的。为了捕捉这种影响关系，本文使用双向GRU（BiGRU）来实现上下文语义的提取。BiGRU可以利用双向通道实现正向和反向的信息积累，从而在物理工作流中获得更加丰富的特征信息。

3.2.4 模型输出

将经过特征工程处理后的工作流特征Fw与BiGRU 的输出outg相融合，得到工作流的最终表示为w，即：

跨平台工作流的最终表示w将被传入至3 层全连接神经网络中进行特征学习，并产生该工作流运行时间的预测结果tw。跨平台物理工作流在GGFN模型中的整体估计过程即为：

其中：Ow为物理工作流的算子特征部分；Fw为物理工作流特征部分。

3.2.5 模型损失函数

在模型训练过程中，本文采用式（10）作为GGFN模型的损失函数，其结合了均方损失（Mean Square Error，MSE）和绝对值损失（Mean Absolute Error，MAE）的优势。在计算损失过程中，当预测偏差小于δ时采用平方误差，当预测偏差大于δ时采用的线性误差，降低了对离群点的惩罚程度，也更具鲁棒性。

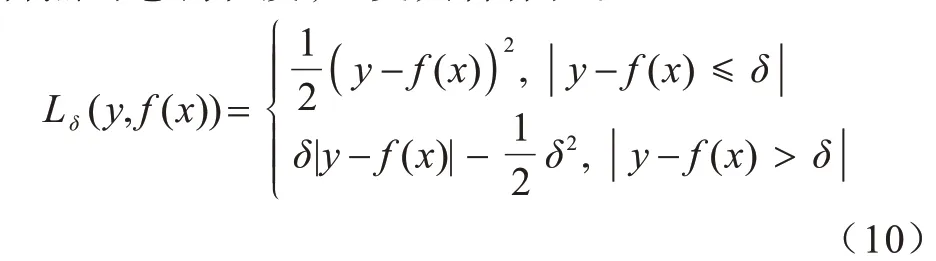
其中：y表示工作流运行时间的真实值；f(x)表示模型运行时间的预测值，超参数δ将根据在训练数据集上的训练效果进行调整。

3.3 算子平台枚举

利用成本模型进行算子平台的枚举并选择成本较低的物理工作流是整个优化方法中必经的一步，但是在进行算子平台枚举过程中会面临笛卡尔积组合造成的指数搜索空间的问题。因此，本文在GGFN 模型的基础上提出了应用剪枝的枚举算法实现将逻辑工作流转换为可执行的物理工作流。

3.3.1 工作流剪枝

假设一个逻辑工作流包含m个算子，每个算子有k个对应的实现平台可以选择，那么如果枚举所有的可能，则将会形成km个物理工作流。研究人员针对该问题提出了其解决办法，如文献［26］使用一种简单的搜索空间修剪技术，即传统贪婪剪枝方法，在枚举过程中仅保留当前步骤下成本最低的物理工作流。这种贪婪剪枝方法虽然简单但是会产生局部最优的结果。而Musketeer［2］使用了动态规划启发式算法返回给定线性顺序的最优k路划分，但是该方法只能探索工作流中算子的单一线性排序，这使得在进行枚举前需要先将DAG 型工作流进行线性排序操作，而这会导致在k路划分时错过可能的算子平台间的阶段划分和合并的机会。为了降低枚举搜索空间并减少优化时间开销，本文提出了较贪婪剪枝方法更加有效且易实现的延迟贪婪剪枝方法，该方法可以在保持工作流结构特点的基础上实现高效的剪枝操作。

由于传统贪婪剪枝方法在枚举过程中仅保留一个成本最低的物理工作流，这样很容易产生局部最优的情况因此延迟贪婪剪枝方法保留了包含两个不确定算子的所有物理工作流，从而在可接受优化开销范围内增加了更多选择。该剪枝方法的主要依据是：如果两个子物理工作流中尾部算子的实现平台相同，那么它们与其他算子连接所需要的数据转换等成本都是相同的。成本低的子工作流在添加算子形成新的子工作流后也将有更低的成本。通过使用该剪枝方法，枚举复杂度将由指数级O(km)降为平方级O(mk2)。

3.3.2 枚举算法及复杂度分析

本文在使用GGFN 模型作为成本模型的基础上，提出了应用延迟贪婪剪枝的算子平台枚举算法，如算法1 所示。

算法1算子平台枚举算法

算子平台枚举算法将逻辑工作流lw 作为输入，并得到最优物理工作流pwmin，其中假设lw 中的算子数量为m。首先，需要对lw 进行向量化处理并拓扑排序得到所有算子的集合（第2 行）。然后，遍历所有算子并枚举其实现平台，将算子及其实现平台放入队列中（第3 行～第6 行），该过程的时间复杂度为O(n)。获取源算子与其实现平台集合作为生成物理工作流向量集合PV 的初始值（第8 行）。接下来将通过循环来添加算子至物理工作流向量。首先是获取当前物理工作流的所有下一个待连接算子及其实现平台集合（第11 行），遍历待连接算子并取其与当前子物理工作流的笛卡尔积进行枚举连接（第12 行～第14 行）。从算子向量中删除已连接算子，然后将不同连接组合所形成的子物理工作流进行剪枝，剪枝将基于GGFN 模型进行，同时更新当前子物理工作流集合（第15 行～第22 行），该过程的时间复杂度为O(n2)。当算子向量队列为空时，枚举连接过程完成，整体过程的时间复杂度为O(mn2)。接着获取PV中成本最低的物理工作流向量并进行反向量化为最优物理工作流pwmi（n第24行），最后返回结果（第25行）。因此，算子平台枚举算法的总时间复杂度为O(mn2)=O(n+mn2)。

本文在GGFN 成本模型对跨平台物理工作流成本准确预测的基础上，通过应用算子平台枚举算法，为每个逻辑算子选择合适的实现平台，并完成从逻辑工作流到物理工作流的优化转换。

4 实验与结果分析

本节通过多组实验来评估本文的优化方法，并证明该方法可以基于GGFN 模型为跨平台工作流中的算子选择合适的运行平台，并利用跨平台系统的多平台优势提高任务的执行速度，GGFN 模型对于成本估计具有更高的准确度。

4.1 实验设置

4.1.1 实验环境

实验在一个由3 个节点组成的集群上进行，每个节点都包含2 个16 核的Intel Xeon Gold 5218 处理器，1 个NVIDIA Tesla T4 GPU，4 个32 GB DDR4 的RAM 以及2 TB 的固态硬盘SSD，操作系统为Ubuntu 20.0.1。部署在集群上的计算平台包括：Java 1.8，Spark 2.4.5，Flink 1.13.2，SparkML 2.4.5，JgraphT 1.4.0，GraphX 2.4.5，Sklearn 0.24.1，Gensim 4.1.0，Tensorflow 2.6，PyTorch 1.7.1。

4.1.2 实验数据集

本文在实验中根据工作流情况使用多个不同的数据集。其中，WordCount 任务与Word2Vec 任务使用Wikipedia 公开数据集，该数据集是源自Wikipedia 网站中用于文本检索的常用典型数据集。PageRank 任务使用斯坦福大学公开数据集LiveJournal-Network，该数据集包含免费在线社区LiveJournal 中近500 万会员及其朋友之间的关联关系，在实验中被用于进行PageRank计算来统计该社交平台中重要用户的权重信息。此外，用于模拟真实计算场景的用户信用分析任务将使用Kaggle 平台上的Credit-Card-Approval-Prediction数据集。该数据集包含欧洲某国用户基本信息与其相关信贷记录的情况，数据集中包括用户信用记录表和用户基本信息表两个部分。其中用户基本信息表主要包括用户编号、性别、教育程度、婚姻状况、出生时间、职业、家庭情况等信息。用户信用记录表主要包括用户编号、记录月份、借贷信用状态。此外，由于上述部分数据集的大小固定，因此需要对其进行数据切片或数据复制等操作，使其可以符合实验中跨平台工作流的输入大小。

4.1.3 实验参数设置及评价标准

在GGFN 模型训练的参数设置中，优化器采用Adam，跨平台工作流的算子特征维度为63，工作流特征维度为39。GAT 网络层数为2，多头注意力K为2，隐藏层节点数为128。BiGRU 网络的层数为2，隐藏层节点数为128。全连接层的隐藏节点数设置为128。模型训练的学习率和Dropout 分别设置为0.001 和0.4。

为了评估GGFN 模型的准确度，本文使用绝对误 差（Absolute Error，AE）及相对误差（Relative Error，RE）作为评价标准，定义如下：

其中：|PW|表示物理工作流的数量；r(∙)表示物理工作流pw 的真实运行时间；e(∙)表示成本模型对pw 的估计运行时间。

4.2 训练数据生成

模型训练需要大量物理工作流及运行时间作为训练数据，但由于跨平台系统为新兴平台系统，因此并没有充足的执行日志作为训练数据。本文的训练数据首先需要通过数据生成的方式产生，然后在系统使用过程中收集执行日志并在线下完成模型训练。本文在文献［27］的基础上改进了其数据模拟方式并生成了用于模型冷启动的训练数据。首先，运行包括少量输入数据的全部工作流以及中等和大量输入数据的少量工作流，并记录运行时间。然后，将已执行的工作流进行标注，同时对结果数据进行多项式插值和数据拟合，并取插值和拟合的均值作为运行时间标签，如图5 所示。

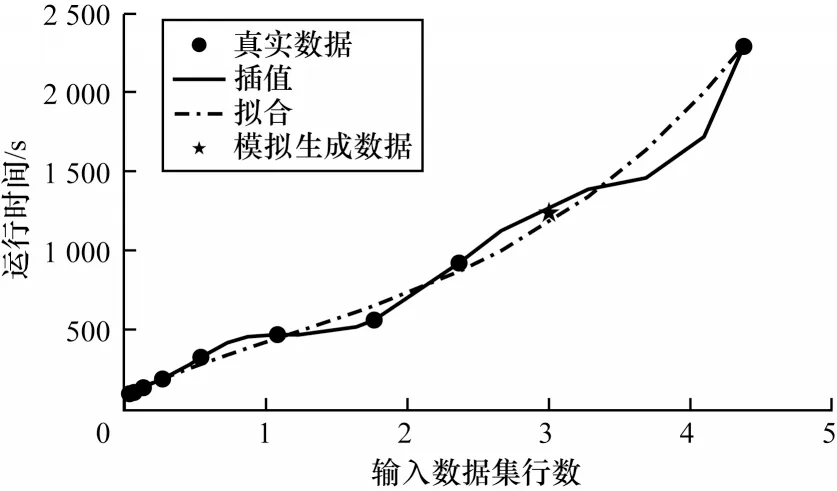
图5 训练数据生成示例Fig.5 Example of training data generation

图5 为某次训练数据生成的示意图。根据工作流输入数据的行数以及实际运行时间，分别对其进行5 阶多项式插值以及3 阶多项式拟合。而对于模拟生成的数据，取插值和拟合结果的均值作为该工作流在指定输入数据集行数的运行时间标签。

4.3 单平台下优化效果分析

首先评估基于GGFN 模型的跨平台工作流优化方法在平台选择时的优化效果。为了使选择效果更加明显，在实验中设置为仅选择一个平台来运行相应的任务工作流。本次实验选择了WordCount、PageRank 和Word2Vec 三个任务作为批处理、图计算以及机器学习任务的工作流代表来进行实验，并分别在不同平台上运行，以此观察优化方法能否为相应的工作流选择最佳的执行平台。图6～图8 显示了在改变数据集大小的情况下3 个不同任务在各自平台下的运行时间。其中，倒三角表示本文优化方法在相应数据输入情况下为工作流选择的执行平台。可以发现，图中结果显示了不同工作流在不同平台上的运行时间是存在显著差异的，部分平台运行时间差距达到5 倍以上，这也表明通过优化为工作流中的算子选择合适的平台对加快任务运行的重要性。

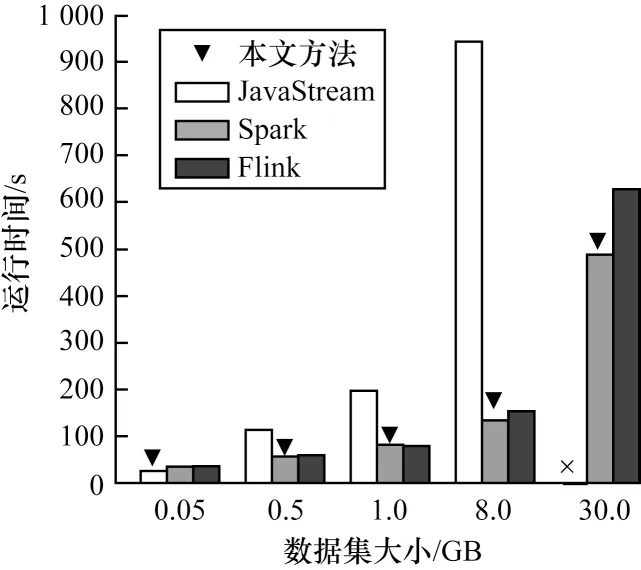
图6 WordCount 任务运行时间对比Fig.6 The comparison of WordCount task runtime

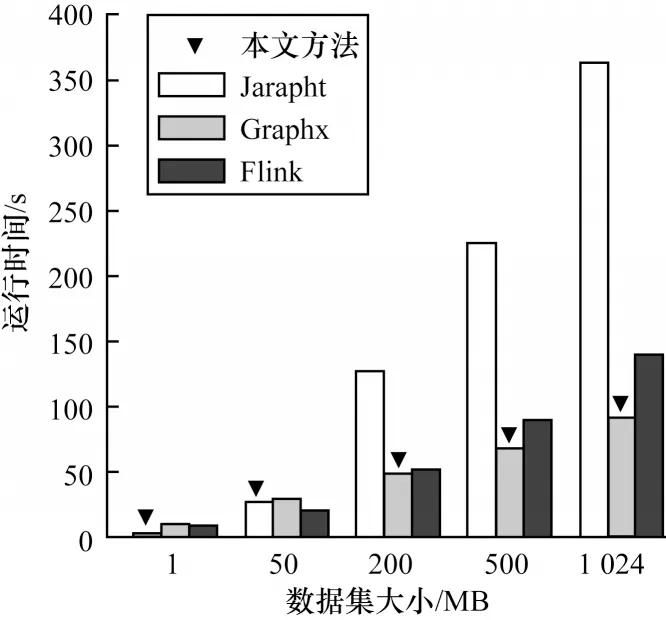
图7 PageRank 任务运行时间对比Fig.7 The comparison of PageRank task runtime

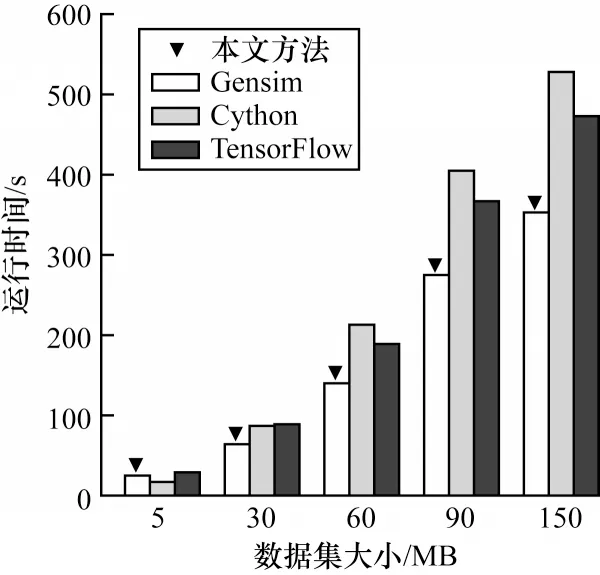
图8 Word2Vec 任务运行时间对比Fig.8 The comparison of Word2Vec task runtime

在图6 所示的WordCount 任务中，当数据集较小时（如0.05 GB），JavaStream 由于单机优势而获得较快的执行速度，而Spark 和Flink 平台却由于分布式通信等开销的影响导致其速度较慢。在数据集大于1 GB 后可以明显发现，JavaStream 的运行时间突增，且在30 GB 时出现运行异常。而Spark 通过分布式节点进行数据处理，与计算时间相比通信开销所带来的影响开始变得很小。基于GGFN 的优化方法发现这一差异并准确地选择出最佳运行平台。

图7 显示了PageRank 进行10 次迭代计算情况下的执行时间。在小规模图上，Jgrapht性能优于其他平台，但在大规模图上，Graphx的性能却是Jgrapht的3～4倍，这是由于平台的定位是面对不同规模的图数据集，而对于图8 中的Word2Vec 任务，由于Gensim 对该算法进行了优化，且使用Cython 提高计算性能，因此在该项任务中一直保持较快的执行速度。

可以看到，在近87%的情况下，基于GGFN 模型的优化方法选择了最佳的执行平台，即使是在两个运行平台时间相差较小的情况下。只有在少数困难的情况下未能选择出最佳的平台，如Word2Vec 任务在5 MB 输入时。因此，可以得出以下结论：基于GGFN 模型的优化方法可以为绝大部分任务选择出最佳平台并防止任务陷入极端的执行情况，如在30 GB 下的WordCount 任务并未选择JavaStream 作为执行平台。

4.4 多平台下优化效果分析

本节将评估基于GGFN 模型的优化方法能否利用多平台优势加速任务工作流的执行。实验使用一个真实环境下的用户信用相关性分析任务作为实验工作流，如图9 所示。该工作流包含11 个算子，使用Credit-Card-Approval-Prediction 数据集作为工作流输入。该数据集包含用户信息和用户信用记录两个部分。该工作流对此数据集进行处理后使用Kmeans 分析影响用户信用的相关因素。

图10 显示了该任务工作流仅在JavaStream、Spark、Flink 的单平台下的运行情况，以及使用了基于GGFN 模型的优化方法为工作流中算子根据情况选择实现平台后的运行情况。可以发现，在输入数据集小于1 GB 时，优化方法仅选择JavaStream 作为执行平台，因为此时的JavaStream 运行时间总是小于其他平台数据处理时间以及中间结果的文件生成所带来的时间开销。当数据集大于1 GB 时，优化方法选择结合JavaStream 和Flink 或者Spark 进行计算。其中，由于算子1～算子3 所在分支的输入数据集（用户信用记录表）仅包含3 列数据，且数据集大小仅为用户信息表的30%，算子ReduceBy 会把数据压缩至输入数据的5%。因此，该分支总是被选择由JavaStream 执行。例如，在输入数据集为2 GB 时优化方法选择了JavaStream 和Spark 平台并将任务工作流分为两部分执行。

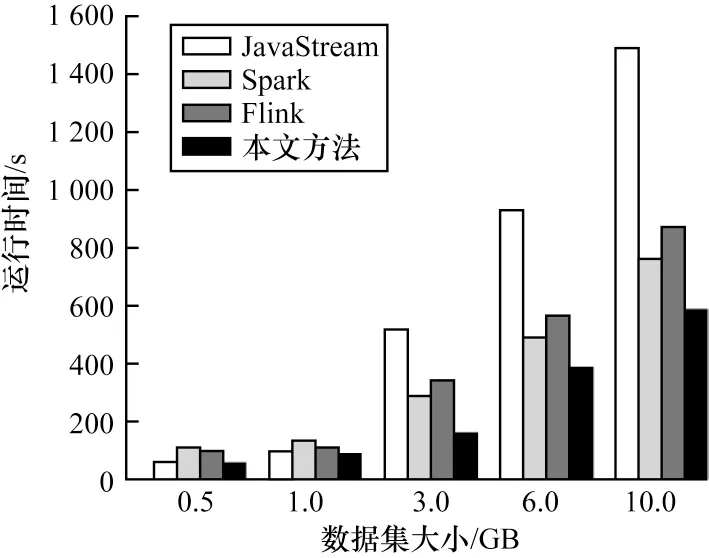
图10 用户信用分析任务运行时间对比Fig.10 The comparison of user credit analysis task runtime

基于GGFN 的成本优化方法利用多平台优势，根据不同情况为跨平台工作流中的算子选择合适的实现平台从而提升性能。在该实验中，使用基于GGFN 的成本优化方法对任务工作流进行优化后，性能较单机最差情况提升近3 倍，运行时间缩短60%以上，性能较单机最好情况提升近25%。

4.5 GGFN 模型分析

成本模型旨在帮助优化方法根据预测的运行成本选择最佳的物理工作流并避免出现最坏的情况，因此准确的成本估计至关重要。为了评估GGFN 模型对于成本估计的准确性，本文根据文献［9］复现了Robopt 优化器中基于随机森林的成本模型。同时为了验证GGFN 模型对于时间和结构信息的提取能力，本文将其与深度神经网络（Deep Neural Networks，DNN）进行比较。DNN 包含8 个隐藏层，每个隐藏层有256 个神经元，其模型输入是算子特征和工作流特征向量的串接。在此基础上，本文在WordCount、Word2Vec、PageRank 和用户信用分析4 个任务上分别评估了GGFN 模型、随机森林（RF）模型以及DNN模型的绝对误差值（AE）以及相对误差值（RE），如表1 所示。

表1 各个成本模型的AE 与RE值Table 1 AE and RE values of each cost model

实验结果表明，GGFN 模型的准确度优于Robopt 中所采用的随机森林模型以及DNN 成本模型。在绝对误差方面，GGFN 比DNN 最高降低了81.1 s，比随机森林模型最高降低了24.9 s。而在相对误差方面，GGFN 模型比随机森林模型提高近14.9%，比DNN 提高达42.6%。由于DNN 模型参数复杂，因此需要更多的训练数据帮助其分析影响成本的因素。虽然此次训练数据来自冷启动和部分执行日志，但仍不足以训练出可以准确估计DAG 型工作流成本的DNN 模型。随机森林模型由于相对简单，因此具有更好的鲁棒性，实验中训练速度最快，使用也相对简单，但在成本预测误差方面与本文中的GGFN 模型相比仍有差距。这也充分说明了GGFN 模型可以利用GAT 和BiGRU 来提取DAG 型工作流中算子的结构和时序信息，以实现更加准确的成本估计。

4.6 优化时间开销分析

本文实验评估了基于GGFN 模型进行跨平台工作流优化过程的时间开销。在跨平台工作流中增加算子来探究优化延迟的变化情况，并通过对比来说明延迟贪婪剪枝的效果。其中每个算子的对应平台数目设定为3，这也是目前算子平均所拥有的平台实现数，实验结果如图11 所示。可以发现，在算子数量小于15 时，基于GGFN 模型的优化时间开销仅比贪婪剪枝算法多1.5 s，但可以最大程度地避免产生局部最优的情况，即使在算子数量为25 时，此时的优化时间开销仍小于3 s，这对于基于GGFN 模型优化方法所带来的性能提升来说是可接受的。为了保证优化效果最大化并降低优化时间开销，因此在枚举过程中使用延迟贪婪剪枝方法可以降低优化时间，相比贪婪剪枝方法也具有较好的优化效果。

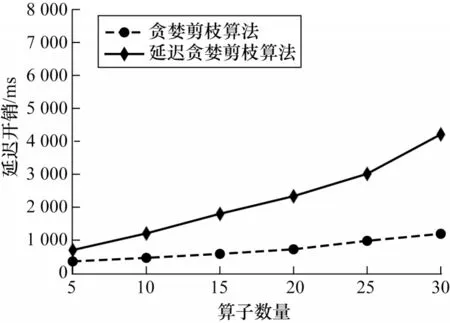
图11 优化延迟开销对比Fig.11 The comparison of optimization delay overhead

5 结束语

在大数据时代，结合多个平台的跨平台数据处理系统开始兴起，而针对跨平台系统的工作流优化由于存在成本预测准确度低等问题而难以实现较好的效果。本文提出一种高效的跨平台工作流优化方法。使用由图注意力网络和门控循环单元组成的GGFN 模型作为成本模型，用来捕捉跨平台工作流的结构信息和算子运行时序信息。基于成本模型的估计结果，通过应用枚举算法为逻辑算子选择合适的实现平台，完成逻辑工作流到物理工作流的优化转换。实验结果表明，基于GGFN 模型的优化方法将现有跨平台工作流性能提升近3 倍，且GGFN 模型可进行更准确的成本估计。后续将进一步优化剪枝方法和平台枚举算法，减少时间开销，并与成本模型相结合，在低延迟开销的情况下实现更好的跨平台工作流优化效果。