基于局部域的影响力最大化算法

沈记全，林 帅，李志莹

（河南理工大学计算机科学与技术学院，河南焦作 454003）

0 概述

随着智能移动设备的普及和5G 网络的应用，社交网络发展迅速。影响力最大化问题作为社交网络分析领域的热点研究问题，旨在从社交网络中寻找k个最具影响力的节点，并最大化以这些节点作为种子节点的最终信息传播范围，被广泛应用于在线广告［1-2］、病毒营销［3］、专家发现［4］、个性化推荐［5］等任务。用户影响力度量是影响力最大化问题的核心。网络拓扑结构［6］是影响力度量的重要依据。与网络拓扑结构相关的影响力度量指标可以分为全局性指标和局部性指标。介数中心性［7］、接近中心性［8］、离心中心性［9］、流介数中心性［10］、Katz 中心性［11］、连通介数中心性［12］等都属于全局性指标。全局性指标需要依靠网络完整拓扑结构，在整个网络范围内计算节点影响力，因此时间复杂度很高。度中心性［13］、半局部中心性［14］、特征向量中心性［15］等都属于局部性指标。局部性指标仅依据局部范围的拓扑信息计算节点的影响力，与全局性指标相比时间复杂度较低。然而，影响力传播具有三度分隔特性，即社交网络中相距三度是强连接，强连接可以引发行为，相距超过三度是弱连接，弱连接只能传递信息。节点有自环［16］特性，拥有自环的节点比没有自环的节点自身活跃度更高，两个节点之间还可能存在多边，这些因素都与节点的影响力密切相关。现有的局部性指标往往忽略这些因素，导致对影响力的度量不够全面，从而影响信息的最终传播范围。

本文结合三度分隔原理［17］，提出用节点在局部范围内的影响力近似其在全局范围内影响力的算法。根据网络拓扑结构构造生成图，依据生成图划分每个节点对应的局部域，根据节点在对应局部域内的影响力筛选候选种子节点。计算每个节点与种子集合的重叠比因子，并据此决定候选种子节点是否能成为种子节点。通过在真实数据集上的实验结果以验证本文算法的正确性和有效性。

1 相关知识

1.1 影响力最大化问题

社交网络可用有向图G=(V,E)表示，其中，V是节点集合且V=｛v1,v2,…，vn｝，E是边集合且E=｛（vi,v）j|vi,vj∊V｝。（∀v）ivi∊V，（∀v）jvj∊V，如果vi对vj产生一次通信行为，则从vi到vj构成了一条有向边

影响力最大化问题是从网络G=(V,E)中找到一个大小为k的节点集合S，最大化以这k个节点作为种子节点开始影响力传播后影响力的最终传播范围（即激活的节点数最多）。影响力最大化问题可表示如下：

其中：S*表示节点集合；f(S*)表示影响力的传播范围。

1.2 影响力传播模型

线性阈值（Linear Threshold，LT）模型［18-19］可以用来模拟影响力的传播过程。在LT 模型中，节点只能处于激活状态或者非激活状态。激活状态的节点通过有向边试图激活处于非激活状态的邻居节点。对于非激活状态的节点，当所有激活状态的邻居节点对其影响力之和大于该节点的激活阈值时，该非激活节点就转为激活状态。当网络中不再有节点被激活（即由非激活状态转为激活状态）时，影响力的传播过程收敛。

图1 给出了根据LT 模型模拟影响力传播的过程，其中，灰色圆表示激活节点，白色圆表示非激活节点，有向边上数字表示箭尾节点对箭首节点的影响力。节点v1、v2、v5和v6为种子节点，在传播开始时处于激活状态；其他节点则处于非激活状态。整个传播过程经过3 轮迭代收敛。

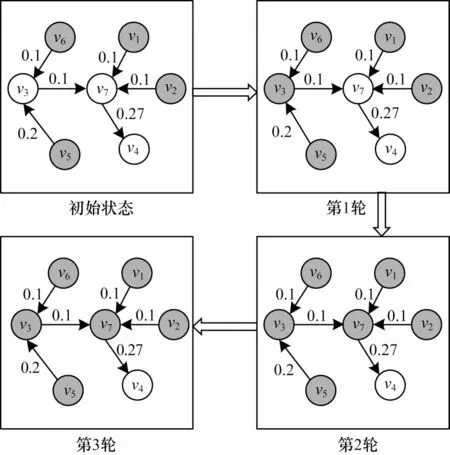
图1 LT 模型上的信息传播示例Fig.1 Example of information dissemination on LT model

2 影响力最大化算法

本文针对局部性度量指标构造生成图，根据影响力传播的三度分隔原理构建局部影响力度量模型，依据局部影响力度量模型设计基于局部域影响力的种子节点选择算法。

2.1 权重感知的生成图构造

边影响权重根据自环和多边属性计算。边权重反映了节点间的亲密程度，影响力的传播过程又受邻居间关系疏密的影响。因此，边影响权重的计算过程中应考虑自环和多边现象。

自环指的是一种特殊的环结构，这种环状结构只包含一个节点。社交网络中用户可能发起只有自己参与的社交活动，从而在对应的社交网络图中形成只有该节点参与的自环。自环多的节点活跃度较高，在信息传播过程中会主动地影响其他节点。本文引入自环因子度量自环对节点能力的影响。自环因子计算如下：

其中：Rvi表示节点vi的自环因子；ψ（vi）表示节点vi每个自环的权重。在无权网络中，ψ（vi）默认为1，此时节点自环因子等于节点的自环个数。

多边指的是社交网络图中两个节点间有多条边存在。在社交网络中，两个节点间的一次互动会在社交网络图中对应的节点间产生一条边。当两个节点间有多次互动时，它们之间就会有多条边。然而，随着边数的增加，图的存储和遍历成本也会增加。在不影响图的存储和计算成本的前提下，本文引入多边因子，用以度量节点间存在的多边现象对信息传播过程的影响。多边因子随着两个节点间边的增多而增大。多边因子计算如下：

结合自环因子和多边因子，本文引入边影响权重，描述节点间的影响力。

定义1给定一条边（vi,v）j，vi对vj的影响力即为该边的边影响权重。边影响权重计算如下：

根据自环因子、多边因子和边影响权重构造生成图，并且生成图是有向带权图。

2.2 局部域影响力度量

影响力的全局性度量指标往往从拓扑结构的整体出发对节点的影响力进行全面准确的衡量，但是却存在计算复杂度高的问题。根据影响力传播遵循的三度分隔原理［17］，即节点的影响力在相距不超过三跳的邻居节点间传播时随着距离的增大而不断衰减，当传播距离超过三跳时几近消失。本文根据三度分隔特性，利用节点的影响力在特定的局部范围内的传播过程来近似其在全局范围内的传播过程。为了度量节点在特定局部范围内的影响力，引入最短距离、局部邻居以及局部域的概念，并结合局部域拓扑结构建立影响力度量模型。

定义2节点间最短路径的长度即为节点间的最短距离。假设（∀v）ivi∊V，（∀vj）vj∊V，若vi到vj的最短路径为p(vi,vj)且p(vi,vj)=则节点vi到vj的最短距离

定义3给定节点vi，若vj是vi的可达节点且到vi的距离不大于D，则称vj是vi的局部邻居。

定义4给定节点及其局部邻居构成的节点集合以及这些节点间的边构成的边集合共同组成此节点的局部域，记为AL。以节点vi为中心的局部域记为AL(vi)，表示如下：

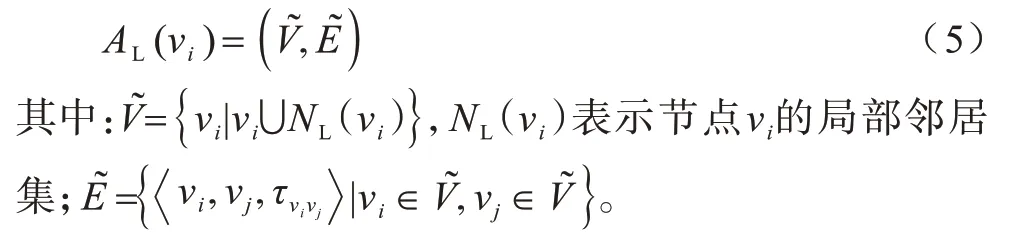
定义5对于给定节点，其局部域影响力为以此节点为中心的局部域拓扑结构所决定的节点传播信息的能力，记为Cr。（∀vi）vi∊V，Cr(vi)计 算如下：

以8 节点网络中节点v1为例说明局部域影响力的计算过程，如图2 所示，其中圆圈内字母及其数字下标表示节点，有向边上的数值代表两节点间的边影响权重。假设D=3，节点v1的局部域由节点v1与其局部邻居节点｛v2，v3，v4，v5｝以及它们之间的边构成。

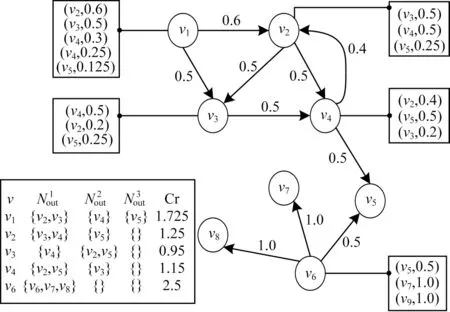
图2 计算节点的Cr 值示例Fig.2 Example of computing Cr values of nodes

2.3 影响力重叠检测

节点之间可能存在影响力重叠现象，导致多个节点的共同影响力小于各节点影响力之和。为了保证影响力的传播范围最大，在选择种子节点时应考虑节点之间可能存在的影响力重叠现象。权衡影响力重叠检测成本和消除影响力重叠后的收益，本文允许影响力重叠，但是应避免影响力过度重叠，并利用式（7）判定给定节点间是否存在影响力重叠。

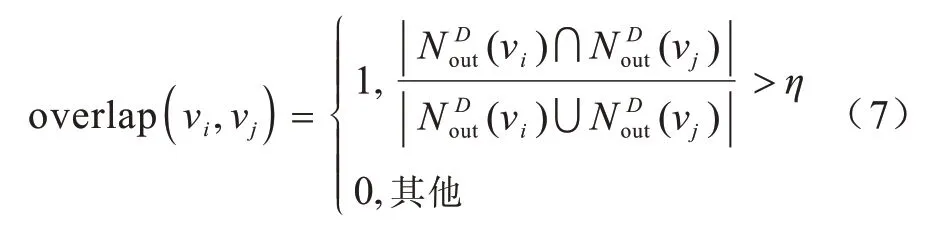
其中：η表示过度重叠判定阈值分别表示vi和vj的出边直接连接的节点构成的集合。在式（7）的基础上，本文定义了重叠比因子，判定一个集合中节点间影响力重叠的程度。

定义6重叠比因子为给定集合中影响力过度重叠的节点在集合中所占的比例，记为ω。给定集合C⊆V，该集合的重叠比因子计算如下：

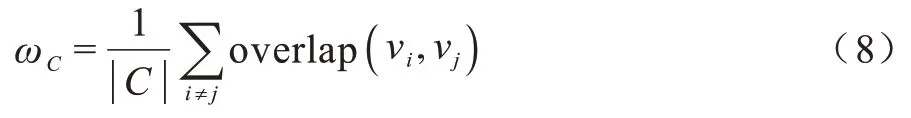
2.4 算法描述

首先根据Cr 值构建候选种子节点列表，并将该列表中第一个节点作为种子加入种子集合。然后依次从候选种子节点列表中选择一个节点，并计算该节点加入种子集合后该种子集合的重叠比因子。若该重叠比因子小于预定义的重叠比阈值，则将此节点加入种子节点集合，否则不能将此节点加入种子集合。重复上述过程，直至选出足够数量的种子节点。算法1 给出了基于局部域的影响力最大化算法的伪代码。

算法1基于局部域的影响力最大化算法

对列表中的每个候选种子节点按顺序挑选，在最坏情况下需要遍历所有候选种子节点。对于每个遍历到的候选种子节点，均要根据式（8）检测是否与某种子节点存在影响力过度重叠。给定种子节点数k，判定某个候选种子节点是否与某个种子节点存在过度重叠的时间复杂度为O(kd)，其中d为节点平均出度。基于以上分析，从节点集合V中选出k个种子节点的时间复杂度在最坏情况下为O(|V|kd)，也可表示为O(|E|k)。除种子集合S外，本文算法对于每个节点还存储了flag和ωS两个变量，且最多为列表中所有节点均设置，因此算法的空间复杂度在最坏情况下为O(|V|)。

3 实验与结果分析

实验选取5 种对比算法，通过在6 个不同规模的真实数据集上比较算法的影响力传播范围、算法运行时间等指标来验证本文算法的正确性和有效性。

3.1 数据集与实验环境

表1 给出了选用的数据集信息，其中，|V|表示节点总数，|E|表示边总数，d为节点平均出度。所有数据集均来自斯坦福大学的大型网络数据集（http：//snap.stanford.edu/data/）。

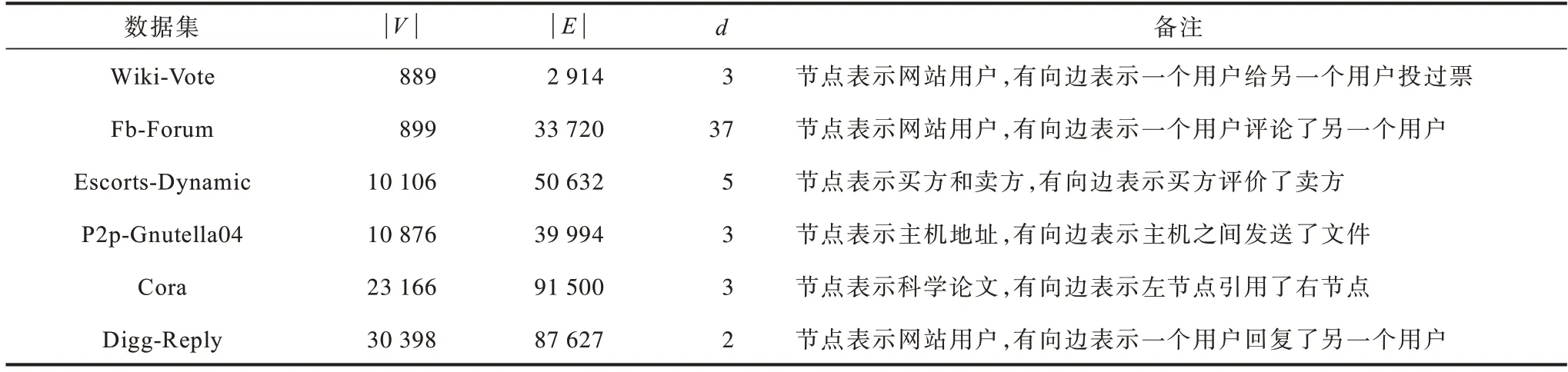
表1 数据集设置Table 1 Dataset setting

实验选用MaxDegree 算法、PageRank 算法、ICGW算法、Closeness 算法和IDD1 算法5 种对比算法。这些对比算法分别采用最大度策略［13］、PageRank 方法［20］、约束贪婪方式下的影响力节点识别方法［21］、Closeness方法［8］和改进的度折扣启发式策略［22］选择种子节点。所有算法均用Python 实现，在相同的Windows 平台上运行。该平台采用Intel Core i5 1.80 GHz 处理器，配置8 GB 内存空间。

实验采用的评价指标分别为影响力传播范围、算法运行时间和占用的内存空间大小。影响力传播范围用激活的节点数表示，该值越大越好，算法运行时间和内存空间占用则越小越好。

3.2 结果分析

在本文算法中，参数η、θ和D分别表示过度重叠判定阈值、线性阈值模型下的激活阈值和局部域范围。在本次实验中，取值分别为0.2、0.4 和3。该部分给出的所有结果都是相关算法独立运行1 000 次计算的平均结果。

图3 给出了各算法的影响力传播范围，其中k表示种子节点数。由图3 可知：本文算法在所有数据集上的种子节点的影响力平均传播范围最大，其次是IDD1 算法和ICGW 算法；本文算法相比 于MaxDegree算法、PageRank算法和Closeness算法所选种子节点的影响力平均传播范围较小；本文算法在Cora 数据集上表现最好，所选种子节点影响力平均传播范围分别是IDD1 算法和ICGW 算法的1.77 倍和1.47 倍；本文算法在Escorts-Dynamic 数据集上表现最差，但影响力传播范围仍是IDD1 算法和ICGW 算法的1.04 倍和1.03 倍。

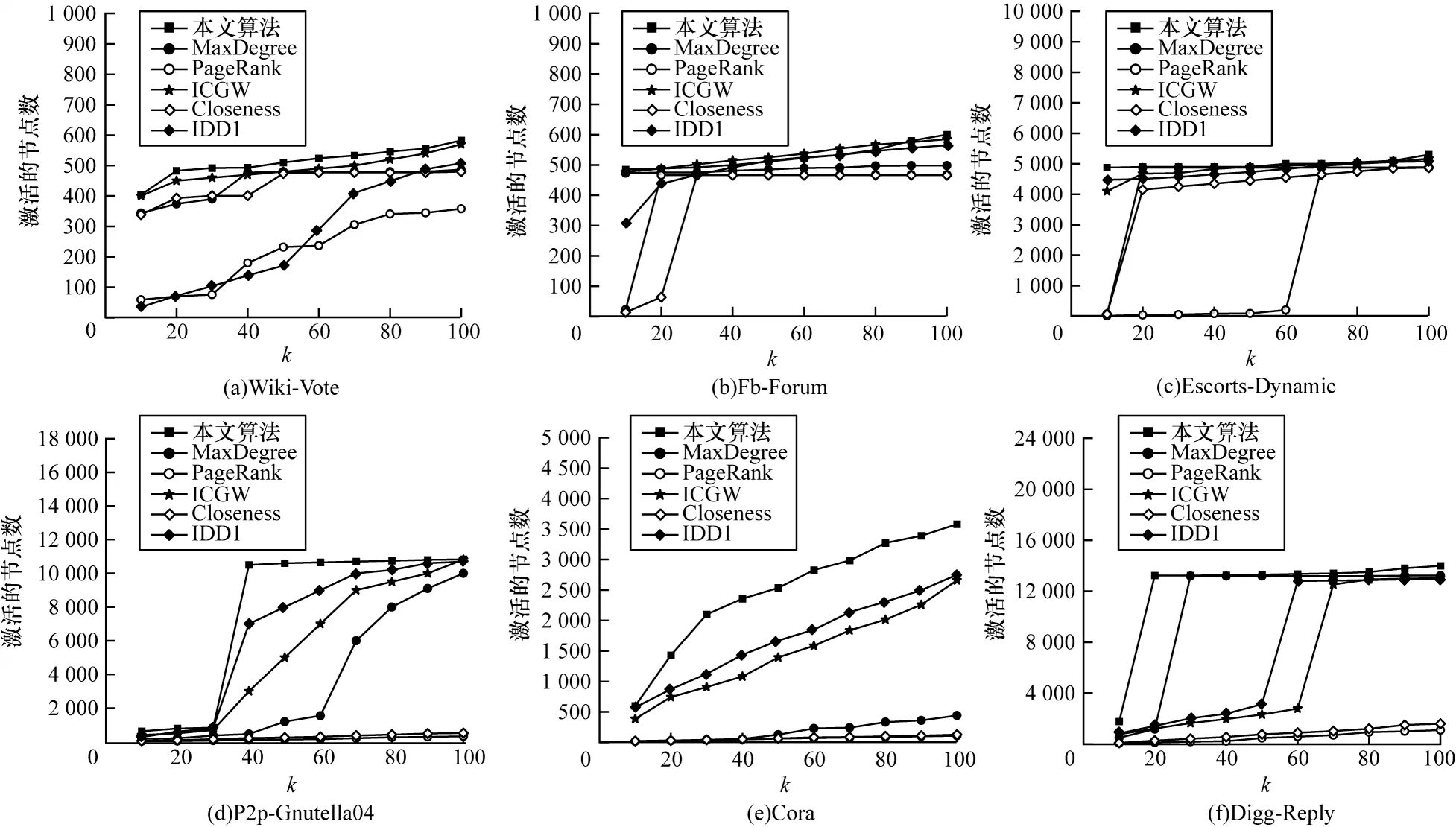
图3 6 种算法的影响力传播范围比较Fig.3 Comparison of influence dissemination range among six algorithms

在种子节点数相同的情况下，本文算法的传播结果始终优于IDD1 算法和ICGW 算法。这是由于本文算法具备影响力重叠控制能力，因此在选择相同的种子时，它对节点的组合影响力更加敏感。在所有数据集上，本文算法的影响力传播范围在种子节点数从10 到50 阶段几乎都呈线性增长，这表明了本文算法识别高影响力节点群体的能力更强。

减少种子节点选择所消耗的时间是本文算法设计的另一个重要目标。图4 给出了在6 个数据集上各种算法选取k个种子节点所用的平均运行时间。总体来看，MaxDegree 算法平均运行时间最短，其次是本文算法、IDD1算法、PageRank 算法 和ICGW 算法，Closeness 算法平均运行时间最长。由于IDD1 算法和ICGW 算法的影响力传播范围和本文算法最为接近，而其他3 种算法的影响力传播范围则远小于本文算法，失去了比较意义，因此在评价算法的时间和空间性能时只与IDD1 算法和ICGW 算法比较。

由图4 可知：本文算法在P2p-Gnutella04 数据集上表现最好，运行时间分别是IDD1 算法和ICGW 算法的7% 和8%；本文算法在Cora 数据集上表现最差，但运行时间仍仅是ICGW 算法的17%；本文算法在Wiki-Vote 数据集和Cora 数据集上的运行时间多于IDD1 算法，但在其他数据集上的运行时间都少于IDD1 算法。因此，从所有数据集来看，本文算法要略优于IDD1 算法。

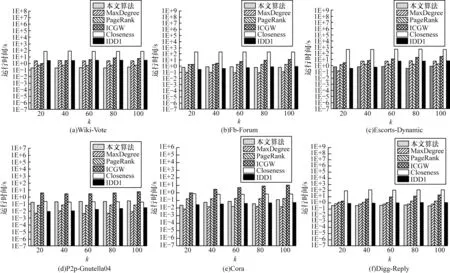
图4 6 种算法的运行时间比较Fig.4 Comparison of execution time among six algorithms

通过实验评估本文算法的空间复杂度。算法在执行过程中占用的内存空间越多，其空间复杂度越高，反之亦然。在实验过程中，随机选择k=50 的运行过程，比较各算法的内存占用情况。表2 给出了在k=50 时各算法在不同数据集上运行时占用的内存空间。由表2 可知：在所有数据集上运行时，本文算法所占用的内存空间均小于ICGW 算法；除了Fb-Forum 数据集和P2p-Gnutella04 数据集之外，本文算法的内存空间占用都低于IDD1 算法。从整体来看，本文算法的内存空间占用情况要优于IDD1算法。

表2 6 种算法在不同数据集上运行时所占用的内存空间Table 2 Memory space consumed by six algorithms when running on different datasets MB

4 结束语

针对度量用户影响力的全局性和局部性度量指标各自存在的局限性，本文利用节点在局部域内的影响力近似其在全局范围内的影响力，提出一种基于局部域的影响力最大化算法。构建以节点为中心的局部域影响力度量模型，依据影响力度量模型筛选候选种子节点集合。利用重叠比因子刻画候选种子节点与种子节点集合间的重叠程度，并根据重叠比因子决定是否将此候选种子节点选作种子节点。实验结果验证了该算法的正确性与有效性。下一步可将本文算法扩展应用于动态社交网络，利用其能高效准确选取高影响力种子节点的优势，设计并实现高影响力节点集合的增量式更新方法。