解三角形、解析几何、微积分、不等式四重奏——两边定和圆内接三角形面积的取值范围

四川省成都市第七中学(610041) 巢中俊 罗志英 张世永

1 研究的问题

带单位外接圆约束且三边之和为定值的三角形面积问题就是单位圆内接三角形的等周问题[1].自然会考虑两边之和为定值的情形,事实上这个问题已有结论:已知ΔABC的外接圆半径为R,sinA+sinC=l(l＜2).则ΔABC面积S的取值范围是

下面将结合解三角形、解析几何、微积分、不等式给出一个有趣的新证明[3].

2 问题的转化

不妨设ΔABC的外接圆半径R=1,于是|BA|+|BC|=2l,则点B是ΔABC的外接圆与一椭圆的一个交点.以边AC所在直线为x轴,边AC的中垂线为y轴建立平面直角坐标系xOy.如图1.

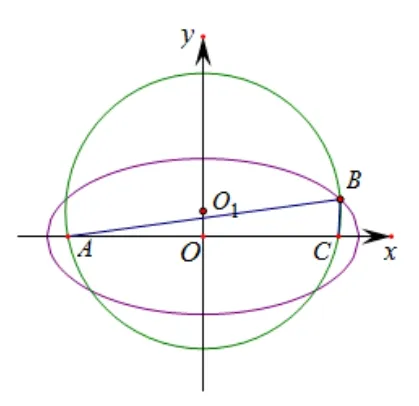
图1

设ΔABC的外接圆圆心O1(0,h),则−1＜h＜1,点B(x,y)满足的方程组是:

的值域问题.下面我们用导数和不等式工具求解这个函数值域问题.

3 转化问题的求解

3.1 情形1

3.2 情形2

对(4)式使用不等式放缩得

3.3 情形3