大矢跨比单层球壳结构的非线性屈曲分析*

姜正荣 邱俊明 石开荣 邓智文 钟宝泉

1.华南理工大学土木与交通学院 广州 510640

2.华南理工大学亚热带建筑科学国家重点实验室 广州 510640

3.广东省建筑工程集团有限公司 广州 510110

引言

单层网壳是目前体育馆、高铁站、候机楼、会议中心等屋盖结构常用的空间结构体系［1－4］，具有结构布置简洁、造型优美以及跨越能力强等优点。

相比于常规的单层球壳结构，清远科技馆单层球壳具有矢跨比大、网格布置稀疏、洞口较大、周边外侧与环形框架相连等特点，在静力荷载作用下难以体现典型单层网壳结构的受力特性［5］。鉴于此，本文对此结构体系进行全过程静力稳定性分析，在特征值屈曲分析的基础上，进一步考察几何非线性、材料非线性、活载的半跨分布及初始几何缺陷分布模式等对其稳定承载力的影响。

1 结构概况

清远科技馆大矢跨比单层球壳跨度24.6m，矢高19.05m，采用肋环型网格形式。球面通过肋杆划分为24 个扇形对称曲面，共有4 圈环杆，最内圈环杆设有十字交叉支撑，球壳两侧开设门洞。其中，洞口A较大，顶标高为12.000m，宽度约为8.6m，洞口B顶标高为3.725m，宽度约为3.1m。在球壳周边外侧设有由环梁及环柱组成的环形框架，环形框架与球壳通过径向的钢梁连接，径向钢梁两端铰接。整体结构如图1所示。

图1 清远科技馆单层球壳Fig.1 Single layer spherical shell in Qingyuan Science Museum

球壳部分采用Q345B钢材，构件均采用焊接箱形截面。其中，最内圈环杆以及十字交叉支撑截面为B600 ×200 ×12 ×12，其余环杆截面为B300 ×300 ×16 ×16 或B300 ×300 ×30 ×30，肋杆截面为B400 ×300 ×20 ×20 或B400 ×300 ×12 ×12；环形框架部分采用Q235B钢材，环柱采用圆管截面P203 ×6，环梁及径向钢梁均采用焊接箱形截面，其规格分别为B200 ×200 ×8 ×8 及B150 ×150 ×6 ×6。

荷载均作用在肋杆或径向钢梁上，其中，永久荷载为2.1kN／m，作用在所有肋杆以及径向钢梁上，活荷载为1.1kN／m，作用在标高大于9.825m的肋杆以及径向钢梁上，边界条件为周边固定铰支座。

采用有限元软件ANSYS 进行稳定性分析，以Beam188 单元来模拟杆件。球壳节点刚接，径向钢梁两端的铰接通过节点自由度释放进行模拟。荷载组合采用1.0 永久荷载＋1.0 活荷载的标准组合。

为深入研究该结构的稳定性能，分别采用了三个计算模型进行对比分析，如图2 所示。其中，模型一将肋杆简化为四段斜杆，杆件弧弯程度不明显；模型二将肋杆细分为多段单元以模拟弧形杆件的受力状态；模型三在模型二的基础上将环向框架去除，仅保留单层球壳结构。

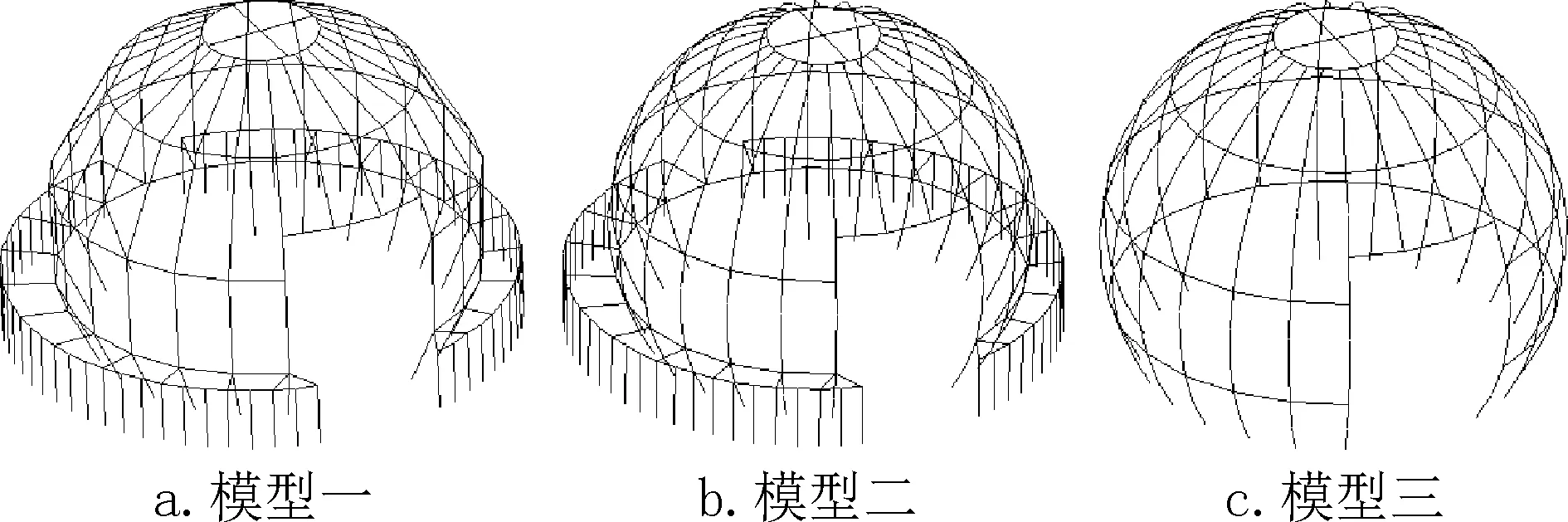
图2 分析模型Fig.2 Analytical models

2 特征值屈曲分析

特征值屈曲分析忽略结构在荷载作用下的变形，是一种线弹性稳定分析，以小位移线性理论为基础，得到结构的特征值和对应的屈曲模态，可为非线性屈曲分析提供参考荷载值，并可作为结构初始几何缺陷施加的确定依据［6］。通过特征值屈曲分析得到三个模型的特征值和对应的屈曲模态，限于篇幅，前十阶特征值如表1 及图3 所示，前六阶屈曲模态如图4 ～图6 所示。

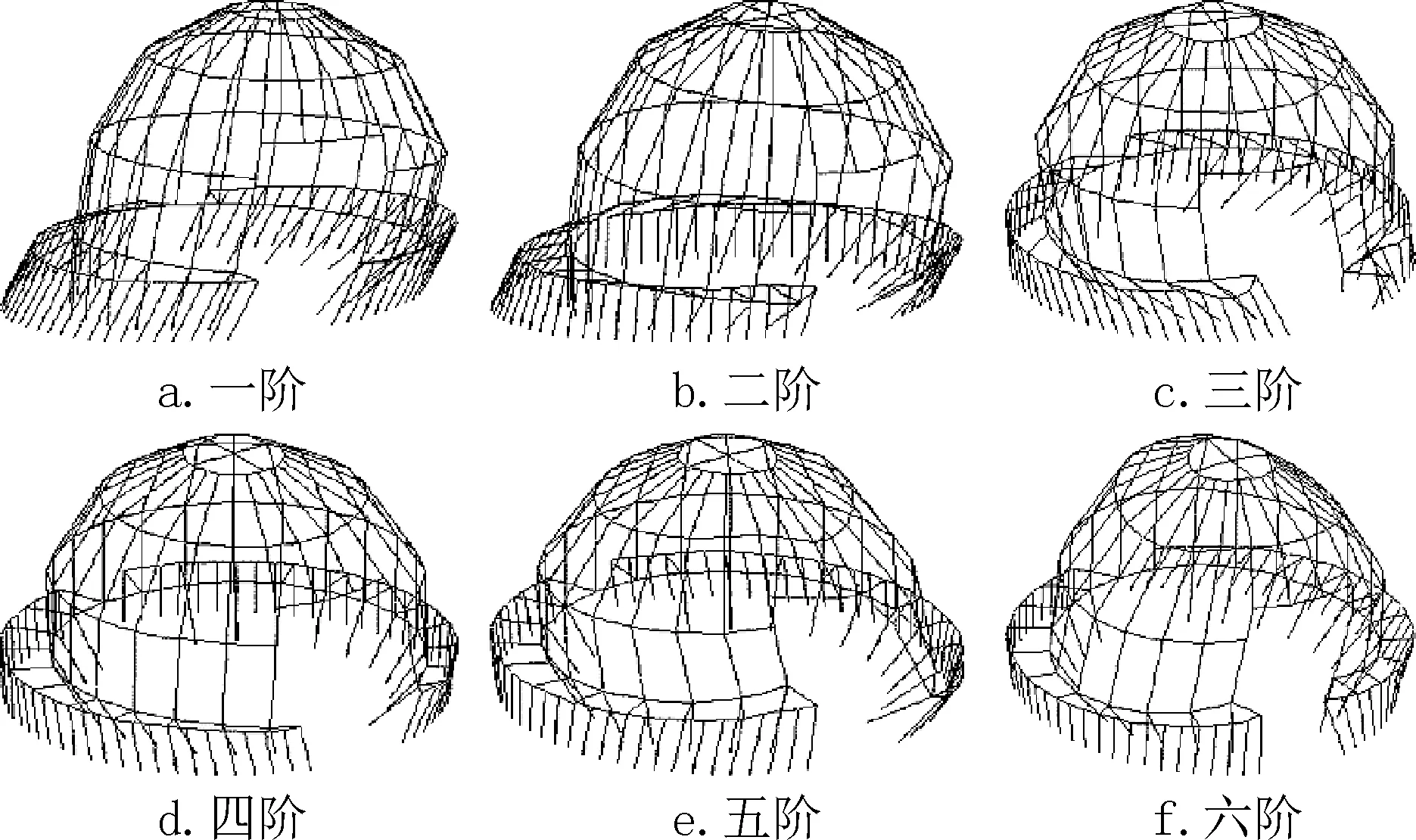
图4 模型一前六阶特征值屈曲模态Fig.4 The first six eigenvalue buckling modes of model 1

由表1 及图3 可见，模型一的各阶特征值均明显大于模型二、模型三，而后两者的特征值比较接近。由此表明，在特征值屈曲分析中，模型二、模型三的特征值较小，结果更为不利，且球壳周边外侧的环形框架对特征值的影响不大。

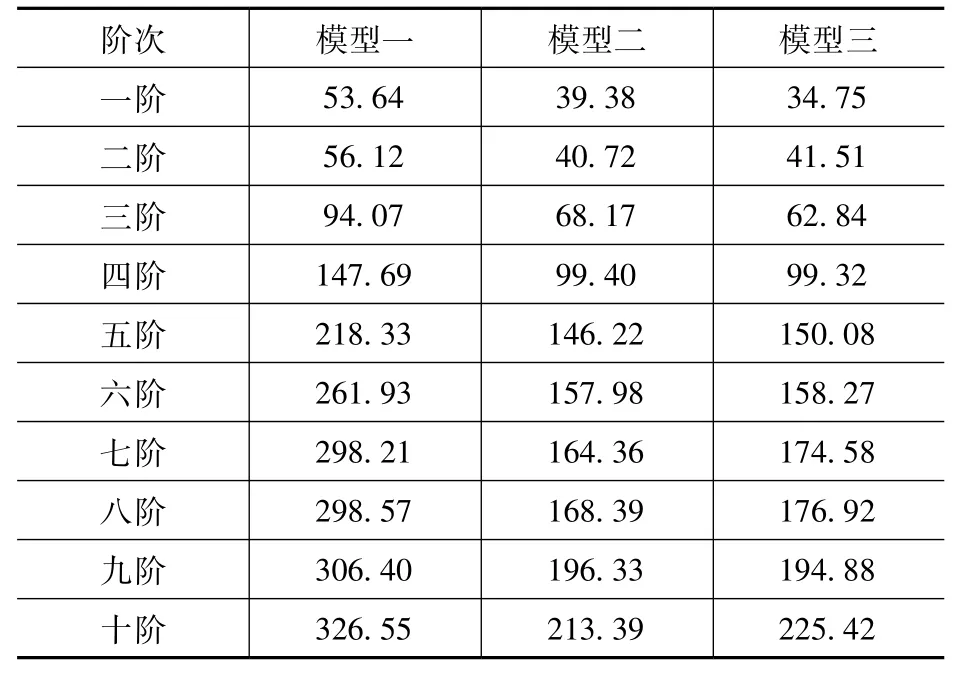
表1 不同模型前十阶特征值Tab.1 The first ten eigenvalues of different models

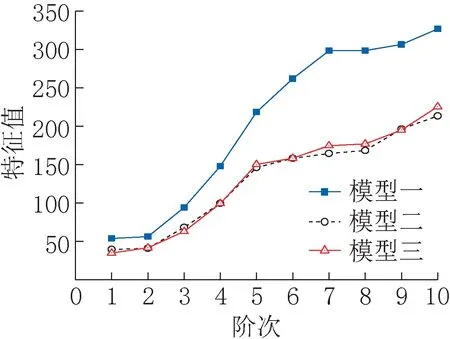
图3 前十阶特征值对比Fig.3 Comparison of the first ten eigenvalues

由图4 ～图6 可见，三个模型的特征值屈曲模态均不同于常规网壳的屈曲模态，未出现点屈曲及条状屈曲等屈曲模态［7］。三个模型的第一阶和第二阶特征值屈曲模态均表现为结构的整体侧移，第三阶屈曲模态为结构的扭转，第四阶和第五阶屈曲模态为球壳洞口A附近的大变形，第六阶模态中模型一与模型二、三不同，模型一为结构的整体下压及洞口A 附近的大变形，模型二、三为结构的整体侧移及下压的耦合。

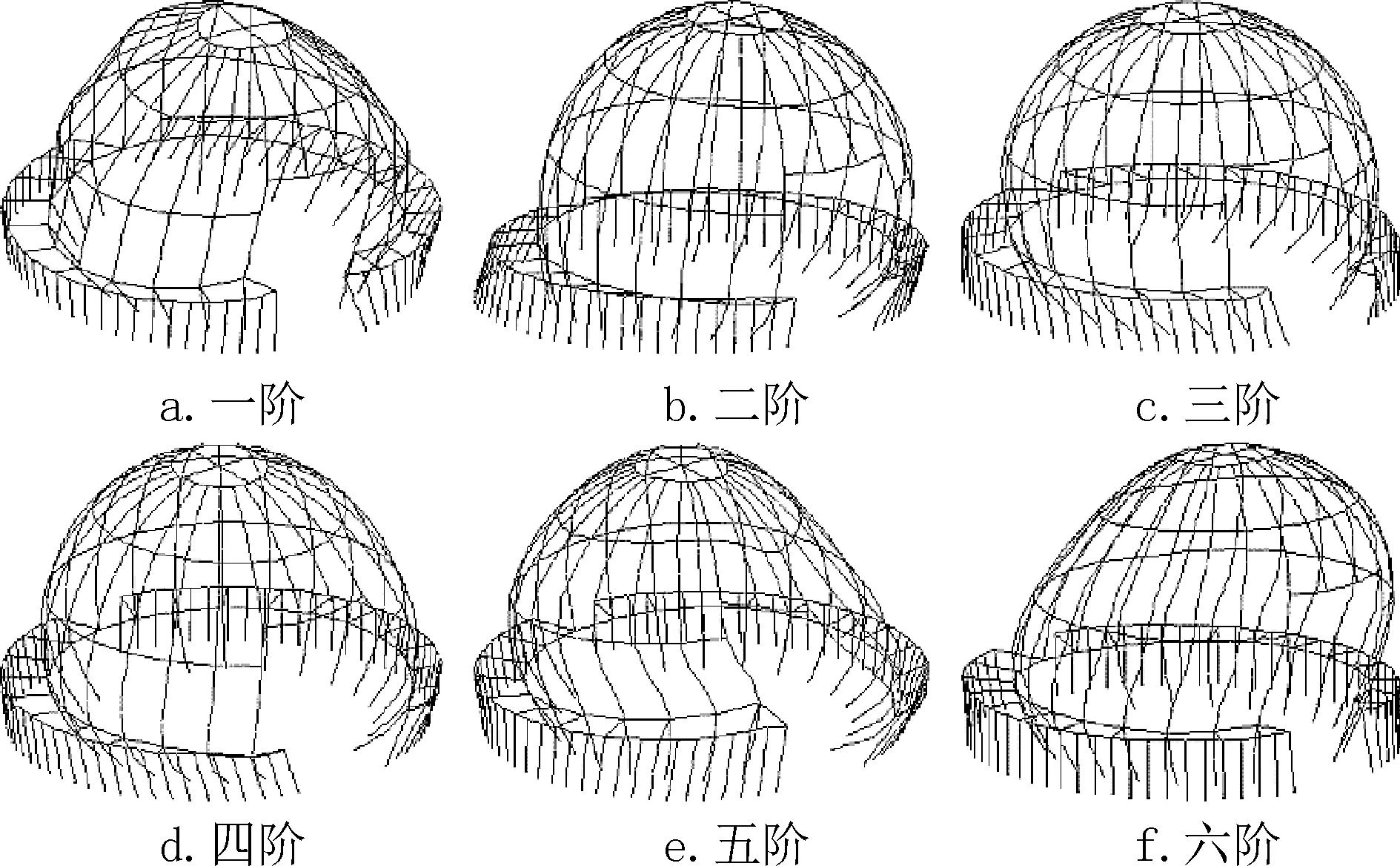
图5 模型二前六阶特征值屈曲模态Fig.5 The first six eigenvalue buckling modes of model 2

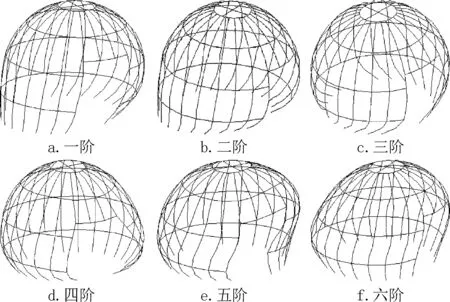
图6 模型三前六阶特征值屈曲模态Fig.6 The first six eigenvalue buckling modes of model 3

3 非线性屈曲分析

对球壳进行非线性分析，包括仅考虑几何非线性以及同时考虑几何非线性和材料非线性的双重非线性。对结构进行非线性屈曲分析，需研究其全过程的平衡路径，得到结构从稳定状态发展到失稳状态的全过程。分析均采用弧长法［8］进行计算，选取球壳结构中计算终止时竖向位移最大的点为参考点，对其进行全过程追踪，获得其荷载-位移曲线。

3.1 理想结构非线性屈曲分析

以理想结构为对象，分别进行仅考虑几何非线性以及同时考虑几何非线性和材料非线性的双重非线性的屈曲分析。非线性材料模型采用理想弹塑性本构关系模型，篇幅所限，Q345 钢材的本构关系如图7 所示。

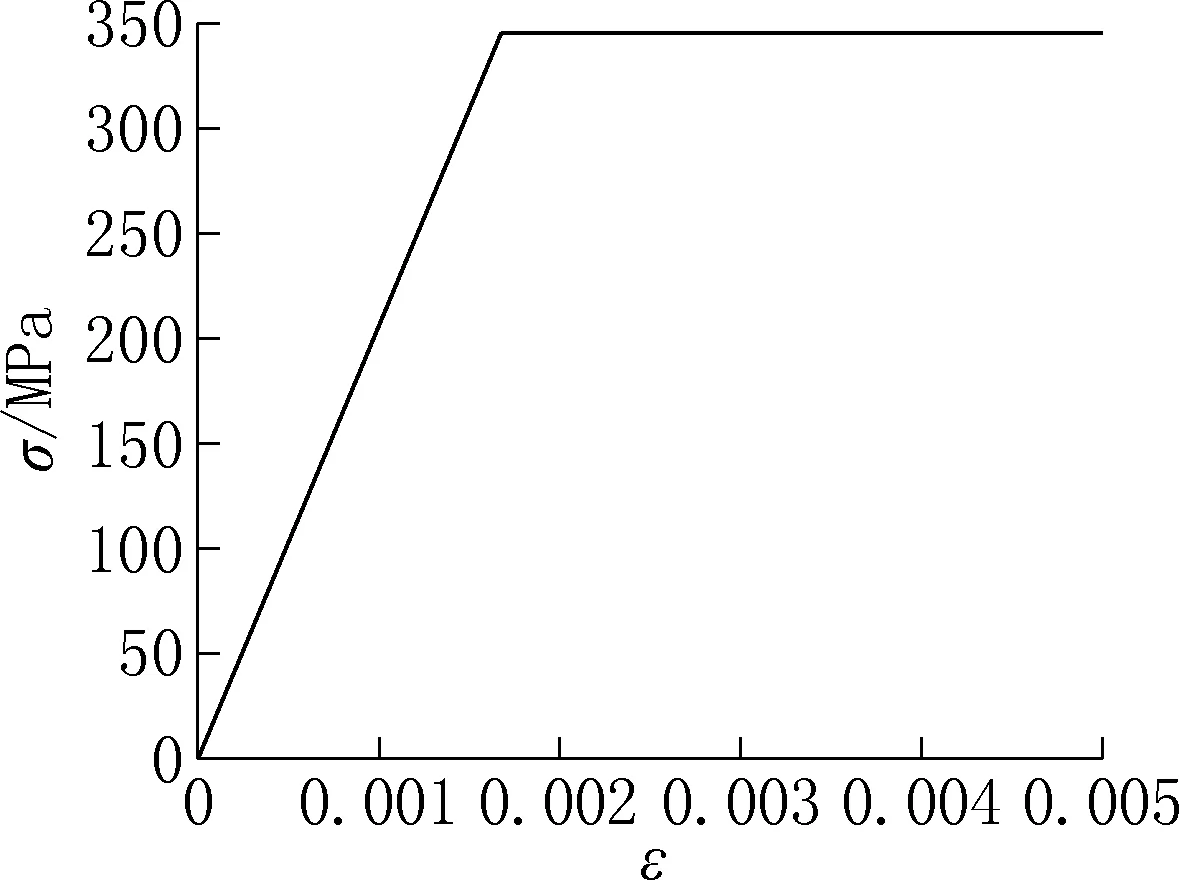
图7 材料本构关系Fig.7 Constitutive relation of material

三个模型在几何非线性及双重非线性条件下的荷载-位移曲线如图8 所示。

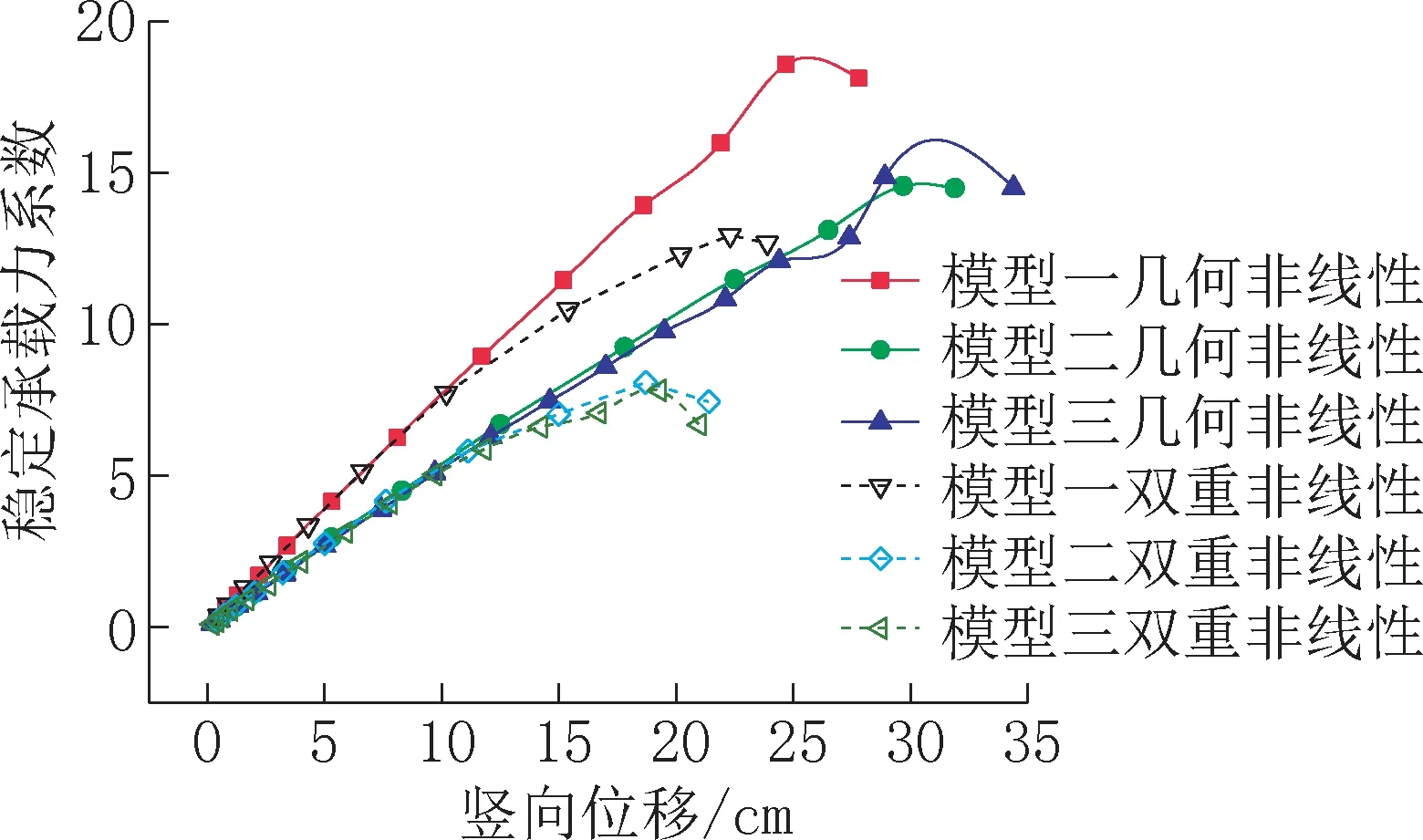
图8 不同模型理想结构的荷载-位移曲线Fig.8 Load-displacement curves of perfect structures of different models

由图8 可见，模型一、二、三在仅考虑几何非线性的条件下，其稳定承载力系数分别为18.576、14.566、14.858，与特征值屈曲分析所得的第一阶特征值相比，分别降低了65.37%、63.01%、57.24%，降幅显著。考虑双重非线性时，其稳定承载力系数分别为12.929、8.085、7.821，与仅考虑几何非线性所得的相应数值相比，分别降低了30.40%、44.49%、47.36%，降幅明显。

三个模型临界点对应的非线性屈曲模态如图9 所示。从中可见，对于理想结构考虑几何非线性及双重非线性，三个模型的非线性屈曲模态均表现为单层球壳侧面洞口A附近区域的屈曲波形较大，这与上文特征值屈曲分析所得的最低阶屈曲模态有明显差异。究其原因，主要是由于该区域大开洞，构件不连续，结构局部刚度较弱造成的。

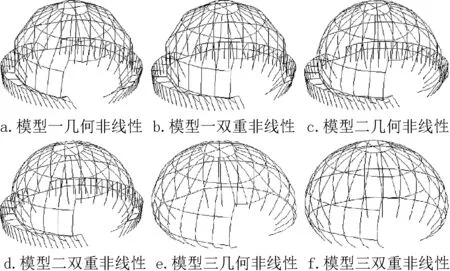
图9 不同模型的非线性屈曲模态Fig.9 Nonlinear buckling modes of different models

由图8 可见，相比于模型一，模型二与模型三的非线性稳定承载力更为不利，且模型二更贴近真实结构，鉴于此，均以模型二为分析对象。

在双重非线性条件下，考虑活荷载的半跨分布，进一步考察其对理想结构稳定性能的影响，共有3 种活荷载半跨分布形式（阴影部分表示活荷载作用范围），如图10 所示。

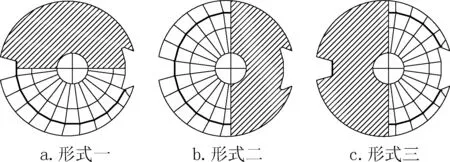
图10 活荷载半跨分布形式Fig.10 Half-span distribution forms of live loads

定义1.0 满跨永久荷载＋1.0 满跨活荷载为组合一，三种1.0 满跨永久荷载＋1.0 半跨活荷载依次定义为组合二、组合三、组合四，四种荷载组合下，理想结构的双重非线性屈曲分析结果如图11 所示。

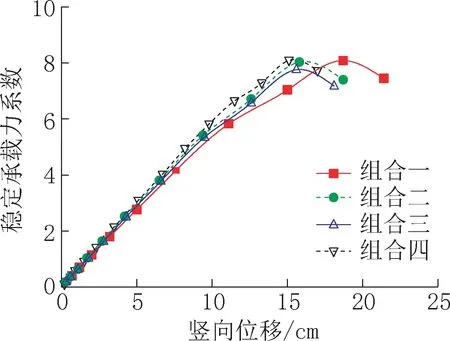
图11 四种组合下的荷载-位移曲线Fig.11 Load-displacement curves under four load combinations

由图11 可见，四种组合下，模型二的弹塑性稳定承载力系数分别为8.085、8.035、7.759、8.096，各组合的稳定承载力系数基本接近，且组合三的稳定承载力系数最不利。因此，对于该结构，活荷载的半跨分布对稳定性的影响并不大。

3.2 缺陷结构的双重非线性分析

对理想结构进行了非线性屈曲分析，然而工程实践中，结构不可避免地存在各种初始缺陷，这些缺陷不同程度地降低结构的稳定承载力。目前，对单层网壳结构初始缺陷的研究，主要集中于初始几何缺陷，即节点安装偏差［9－11］。考虑初始几何缺陷的影响，对模型二进行双重非线性屈曲分析。荷载组合采用组合一，缺陷引入方式为一致缺陷模态法。

一致缺陷模态法，即采用特征值屈曲分析所对应的最低阶模态来模拟结构的初始几何缺陷分布，通过一次计算求得有缺陷结构的稳定承载力系数。此方法应用较方便，且计算量较小，是相关规范［12］所推荐的方法。该方法是将最低阶特征值屈曲模态作为结构的初始几何缺陷分布模式施加到每个节点的空间位置上，缺陷最大值取结构跨度的1／300。采用一致缺陷模态法计算所得的荷载-位移曲线对比如图12 所示。

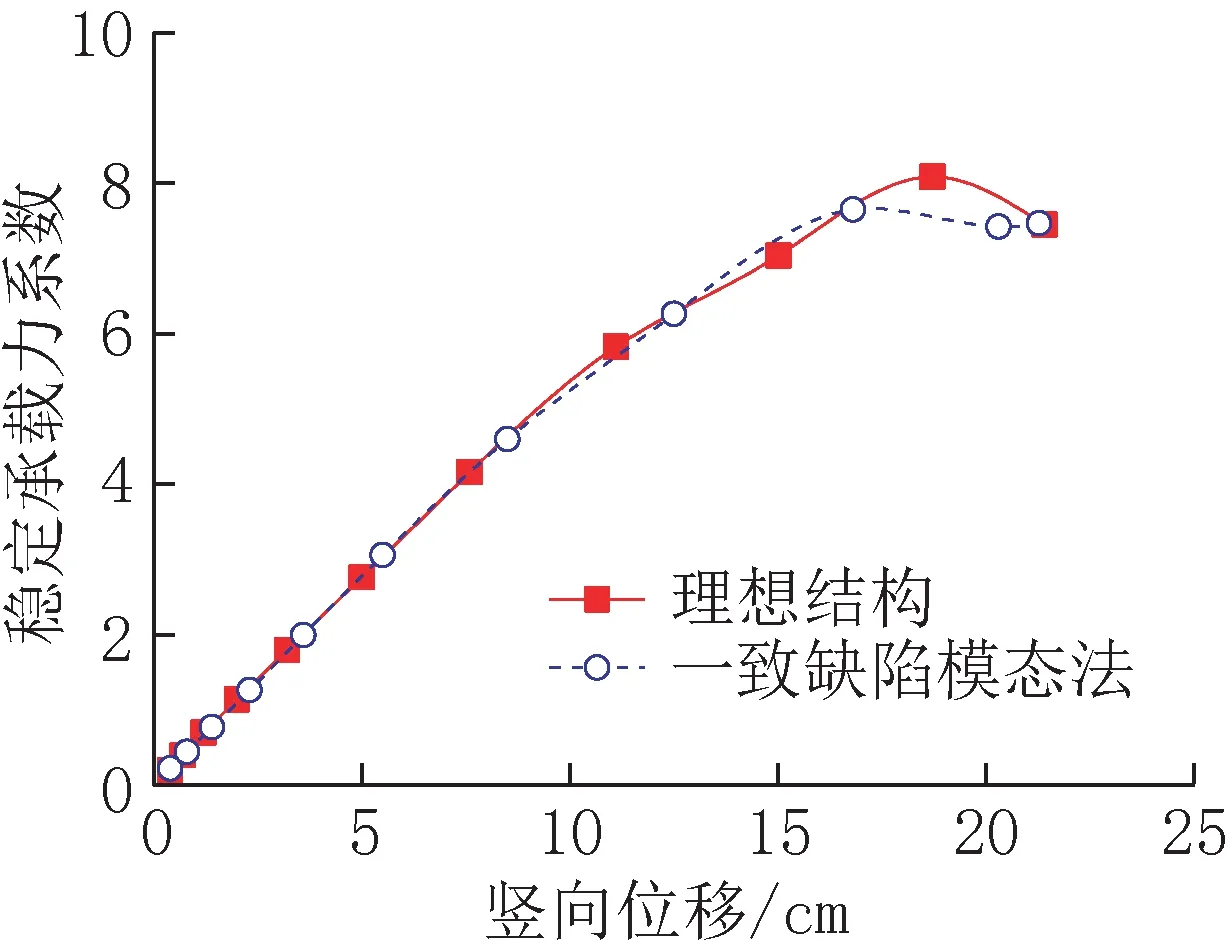
图12 荷载-位移曲线对比Fig.12 Comparison of load-displacement curves

由图12 可见，由一致缺陷模态法所得的弹塑性稳定承载力系数为7.647，而理想结构考虑双重非线性的稳定承载力系数为8.085，仅降低了5.42%，由此表明，该结构对初始几何缺陷不敏感。研究表明，当初始几何缺陷按最低阶屈曲模态分布时，所得的稳定承载力系数并非最不利［13－15］。为进一步考察初始几何缺陷分布模式对结构稳定性能的影响，分别取该模型特征值屈曲的前十阶屈曲模态作为初始几何缺陷的分布模式，以此进行双重非线性分析，结果如表2 所示。

由表2 可见，分别以前十阶特征值屈曲模态作为结构的初始几何缺陷分布模式，求得的弹塑性稳定承载力系数均大于2.0，满足相关规范［12］的要求。此外，当初始几何缺陷按第三阶屈曲模态分布时，所得的稳定承载力系数最不利为6.281。

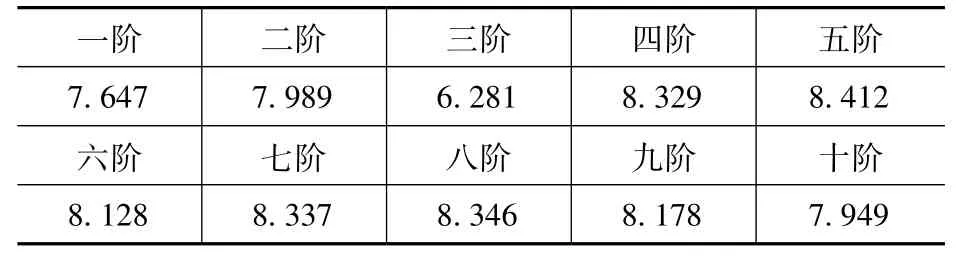
表2 前十阶特征值屈曲模态对应的稳定承载力系数Tab.2 Coefficients of stability bearing capacity corresponding to the first ten eigenvalue buckling modes

4 结论

1.三个球壳模型的前若干阶特征值屈曲模态基本相同，而非线性屈曲模态均表现为球壳侧面洞口A附近区域的屈曲波形较大，这与特征值屈曲分析所得的最低阶屈曲模态有明显差异，表明该部位结构的刚度较弱。

2.模型二更贴近实际结构，且其非线性稳定承载力较为不利；活荷载的半跨分布对该结构稳定性的影响并不大。

3.该大矢跨比球壳结构对初始几何缺陷不敏感；分别以前十阶特征值屈曲模态作为结构的初始几何缺陷分布模式，所得的最不利弹塑性稳定承载力系数为6.281，满足相关规范要求。