风电机组钢-混凝土混合结构塔筒自振频率实用计算方法研究*

张晓钊 周绪红 王宇航 邓晓蔚

1.重庆大学土木工程学院 400035

2.香港大学 999077

引言

随着煤、石油、天然气等传统能源的逐渐枯竭，绿色、清洁、可再生的风能日益受到人们的关注［1］。为了更好地利用风能，风电机组钢-混凝土混合结构塔筒成了当下的研究热点，该结构将钢塔与混凝土塔两种塔筒形式组合，下部为混凝土塔段，上部为钢塔段，如图1所示。混合结构塔筒充分发挥了混凝土受压而钢材受拉的力学性能，具有刚度大、抗疲劳性能好等优势，在我国低风速区风电能源开发中具有广阔的应用前景。

图1 钢-混凝土混合结构塔筒Fig.1 Steel-concrete hybrid tower

风电机组塔筒是一种高耸结构，自振频率较低，容易和风轮的转动频率接近，从而引发共振，对结构不利。在塔筒设计时，第1 阶自振频率是主要的控制因素之一。目前在方案选型和投标阶段，均采取建立精细化有限元模型来求解塔筒的自振频率，此方法固然可以得到精度较高的解，但在设计时，每更改一次参数就需要重新建立塔筒的有限元模型，重新定义属性参数、设置边界条件、划分网格、计算等，效率低下，不利于工程设计。

目前，对于塔筒自振频率理论计算公式的研究相当匮乏，尤其是对于钢-混凝土混合结构塔筒。本文通过理论推导，得到了混合结构塔筒振动的频率方程，并分析了材料密度、混凝土塔段高度占比系数、混凝土塔段与钢塔段壁厚比、锥度等参数对其1 阶自振频率的影响，通过参数修正得到了钢-混凝土混合结构塔筒自振频率的解析计算公式，以期提高工程设计效率。

1 计算假定

为推导出混合结构塔筒自振频率的计算公式，做出如下假定，简化力学模型如图2 所示。

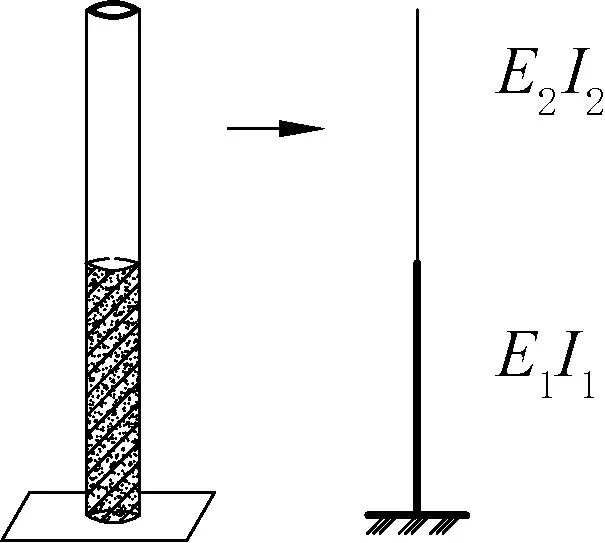
图2 简化模型Fig.2 Simplified model

（1）在推导时忽略塔筒的锥度，推导完对理论解进行锥度修正；

（2）塔筒与地面刚接；

（3）塔筒力学性能在横截面内的各个方向上无差别。

2 频率方程的推导

2.1 混凝土段高度占比系数μ的定义

研究对象是钢-混凝土混合结构塔筒。由于上部与下部的材料不同，混合结构在计算动能与势能时需要分段考虑，对于分界点处的高度，做出如下定义：

式中：μ为混凝土段高度占比系数，Hc为塔筒混凝土段高度，H为塔筒总高度。μ 的物理意义是混合结构塔筒中混凝土段所占的高度比例，如图3 所示。分界点高度可表示为Hc＝μH。

图3 模型截面Fig.3 Simplified model

2.2 振动方程的推导

基于Hamilton原理进行推导，力学计算模型如图4，推导中分别为截面外径（m）、弹性模量（Pa）、截面惯性矩（m4）、截面壁厚（m）、分布质量（kg／m）、材料密度（kg／m3）、截面面积（m2），下标c、s 分别代表混凝土塔段与钢塔段。

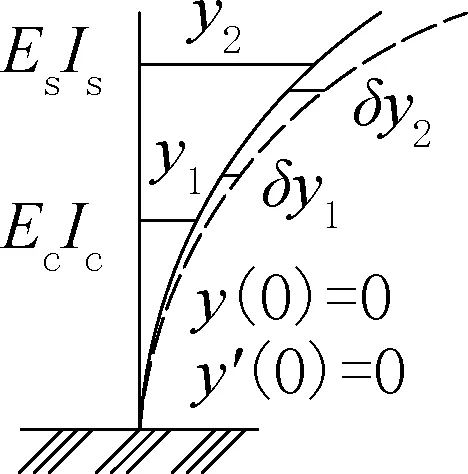
图4 力学计算模型Fig.4 Mechanical calculation model

Hamilton原理表明：当积分上下限给定时，在所有可能的运动轨迹中，真实的运动应使得Hamilton泛函取得极小值，即Hamilton 泛函的1阶变分等于零［2，3］：

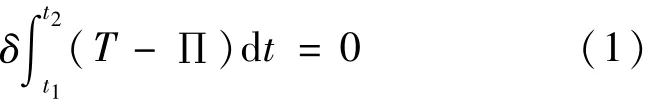
结构的自振频率与外荷载无关，其动能可表示为式（2），势能可表示为式（3）：

式（2），式（3）代入式（1），得混合结构塔筒振动的变分方程：

该变分方程对任意位移扰动δy1，δy2，转角扰动均成立，可推导得振动方程式（5）与自然边界条件式（6）：

2.4 边界条件的化简处理

根据计算假定2，塔筒与地面刚接，由几何关系，位移边界条件为：

沿分界点处将结构切开，如图5 所示，该截面两侧位移，转角，弯矩，剪力均相等［4］，即：

图5 分界点计算模型Fig.5 Calculation model at dividing point

且在分界点处，曲线连续，故有：

将式（7），式（8），式（9）代入式（6），化简后可得混合结构塔筒振动的边界条件：

2.5 振动方程的求解

假设混合结构塔筒任意一点的位移为：

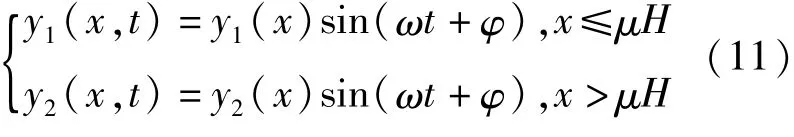
式（11）代入式（5），并求解，得到振动微分方程的通解为［5］：

2.6 频率方程的建立

将边界条件代入振型通解，即将式（10）代入式（12）并化简，得到矩阵方程：

化简后的式（14）是一个六阶矩阵方程，该方程有非零解［6］，则：

式（15）即为混合结构塔筒振动的频率方程。令μλ1H＝x，x由方程式（15）解出，此时的工程频率为：

3 有限元模型验证

3.1 有限元建模计算结果

根据混合结构塔筒高度、外径、混凝土段高度占比系数不同，设计了9 组参数模型，混凝土塔段与钢塔段均为圆形薄壁截面，每组内μ 从0.4 等距0.05 增长到0.6，tc＝0.3（m），ts＝0.025（m），其余参数如表1 所示。使用ABAQUS

表1 模型参数Tab.1 Model parameter

软件建立这9 个组的有限元模型，材料参数设置为Ec＝3 ×1010（Pa），Es＝2 ×1011（Pa），ρc＝2200（kg／m3），ρs＝7850（kg／m3），材料属性设置为均质。分析步采用线性摄动——频率，计算方法采用子空间迭代法，边界条件设置为底边完全固定，网格划分时采用四面体网格，尺寸设置为0.5m。计算结果如图6 所示。

图6 有限元计算结果Fig.6 Finite element calculation results

3.2 频率方程计算结果

求解这9 个组中不同参数对应的频率方程，并通过式（16）解出对应的1 阶自振频率，如图7所示。结果表明，不同参数下频率方程计算结果均比有限元模拟高10%左右，说明频率方程计算结果与有限元吻合良好。由于偏差较小，且偏差集中，认为方程具有较高的价值。

图7 频率方程计算结果Fig.7 Frequency equation calculation results

4 参数分析与处理

显然，式（15）没有参数解。为了得到一个便于计算的1 阶自振频率解析表达式，将通过参数分析化简方程，求得该矩阵方程的参数解。

4.1 材料参数的处理

本研究针对钢-混凝土混合结构塔筒，其属性参数Ec、Es、ρs可认为是常量。对于混凝土的密度ρc，其值常在2000 ～2500（kg／m3）变化，选取表1 中组1、组2、组6 和组7，并取μ ＝0.5，计算这4 组中ρc从1800 变化到2600 时，对应的1 阶自振频率，如图8 所示。

图8 f1 －ρc 关系曲线Fig.8 Curve of f1 and ρc

结果表明，ρc在1800 ～2600 变化时，对频率计算结果的影响小于1%，因此求解式（15）时材料属性参数取为Ec＝3 ×1010（Pa），Es＝2 ×1011（Pa），ρc＝2200（kg／m3），ρs＝7850（kg／m3）。

4.2 频率方程参数解分析

α表示截面内外径之比，混凝土塔段与钢塔段截面类型均为同种薄壁型截面，故：

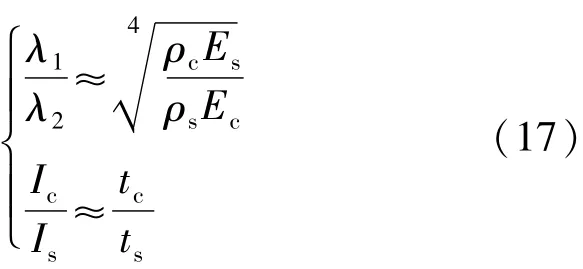
将式（17）及材料参数代入式（15），结果表明频率方程的解x仅跟μ与tc／ts有关，当μ与tc／ts

确定时，频率方程的解x将被确定。在实际工程中，一般有μ∈［0.3，0.7］和tc／ts∈［7，15］。为了得到频率方程的参数解，固定μ ＝0.5 及tc／ts＝12，得到方程的解后再对参数μ与tc／ts进行修正。

图9 εμ －μ 关系曲线Fig.9 Curve of εμ and μ

4.3 参数μ的处理

对于表1 中的9 组模型，求解出μ从0 变化到1 时，每组对应的频率方程，并通过式（16）解出对应的f1，如图10 所示。结果表明f1随μ 的增加先增大后减小。

图10 f1 －μ 关系曲线Fig.10 Curve of f1 and μ

相关系数R＝0.9982，结果如图11 所示。

图11 εμ（μ）拟合曲线Fig.11 Fitting curve of εμ（μ）

4.4 参数tc／ts 的处理

选取表1中组1、组2、组6与组7，并取μ ＝0.5，计算这4组中tc／ts从0 变化到15时，对应的1阶自振频率，如图12所示。结果表明，f1随着tc／ts的增加而增加。tc／ts对结果有一定影响。

图12 f1 －tc／ts 关系曲线Fig.12 Curve of f1 and tc／ts

固定tc／ts＝12，并记εt表示tc／ts这一项的修正系数，使用1stOpt 软件对这4 组数据进行拟合，得到：

相关性系数R＝0.9990，结果如图13 所示。

图13 εt（tc／ts） －tc／ts 关系曲线Fig.13 Curve of εt（tc／ts）and tc／ts

5 频率解析式的求解

取μ ＝0.5 以及tc／ts＝12，求解化简后的频率方程，得：

将式（20）、Ic＝I、Ac＝A代入式（16），并代入修正系数，得混合结构塔筒的1 阶自振频率：

式中：H为塔筒总高度（m），I、A分别为塔筒底截面惯性矩（m4）与截面面积（m2）。εμ（μ）与εt（tc／ts）为修正系数，表示为了得到六阶矩阵方程的参数解而做的修正。

6 理论解的修正

6.1 多元非线性修正

式（21）为解简化频率方程得到的1 阶自振频率解析式，而不同参数下频率方程比有限元计算结果高10%左右。为了得到更加准确的计算公式，需要对理论解进行偏差修正。记偏差修正系数为ξ ＝fFEA／f1，f1表示式（21）计算结果，fFEA表示相同参数下有限元计算结果，ξ 的物理意义是理论公式需要修正的倍率，使用1stOpt软件对表1中9 个组模型进行多元非线性拟合，得到的修正函数如下：

相关系数R＝0.9574，修正后的理论公式与有限元计算结果对比如图14 所示，此时有：

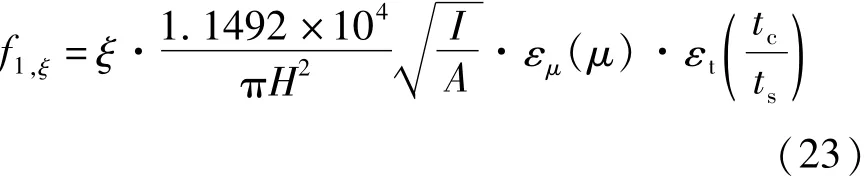
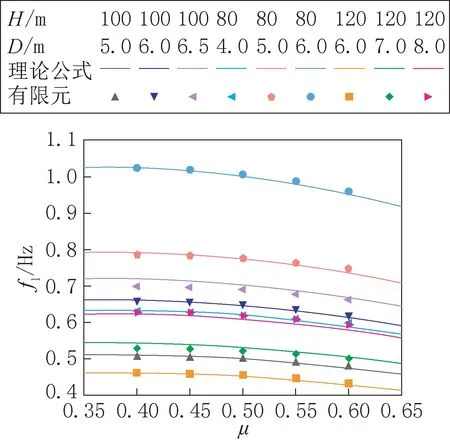
图14 多元非线性修正结果Fig.14 Multivariate nonlinear correction results

同时，为了验证理论公式的可靠性，还设计了10，11 两组参数模型，底部外径均为6m，其余参数见表2，分别用有限元与理论公式（23）计算其1 阶自振频率，结果高度吻合，如图15所示。

图15 壁厚比验证Fig.15 Wall thickness ratio verification

6.2 锥度修正

根据计算假定1，在推导时忽略了塔筒锥度的影响，而实际工程中，塔筒具有一定的锥度，一般θ∈［0，0.025］。因此，对推导出的理论公式还需要进行锥度修正。设计了12，13 两组参数模型，tc、ts均为0.3m 和0.025m，其余参数见表2。

记锥度修正系数κ（θ）＝fFEA，θ／f1，ξ，θ表示塔筒锥度，κ（θ）表示锥度修正系数，fFEA，θ表示考虑锥度时有限元模型计算结果，f1，ξ为公式（23）计算结果。κ（θ）的物理意义是考虑塔筒锥度时，理论公式需要修正的倍率。使用1stOpt 软件对表2中12、13 两组模型的κ（θ）计算结果进行拟合，得到的结果如下：

表2 模型参数2Tab.2 Model parameter of group 2

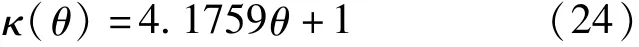
相关系数R＝0.9799，锥度修正后的理论公式与有限元计算结果对比如图16 所示。

图16 锥度修正结果Fig.16 Taper correction results

7 自振频率计算公式

综上所述，钢-混凝土混合结构塔筒1 阶自振频率计算公式如下：

式中：H为塔筒总高度（m），I、A分别为塔筒底截面惯性矩（m4）与截面面积（m2），μ 为混凝土段所占的高度比例，tc为混凝土段截面壁厚（m），ts为钢塔段截面壁厚（m），θ 表示塔筒锥度；εμ（μ）、εt（tc／ts）为使六阶矩阵方程得到参数解的修正系数，见式（18）、式（19）；ξ为理论公式与有限元之间的偏差修正系数，见式（22）；κ（θ）表示锥度修正系数，见式（24）。

8 结论

1.通过理论推导得到了混合结构塔筒振动的频率方程，该方程的解与有限元计算结果吻合良好。并通过参数分析，参数修正得到了钢-混凝土混合结构塔筒的1 阶自振频率计算公式。

2.混凝土的密度ρc波动较大，但在其正常波动范围内，ρc对1 阶自振频率f1的影响非常小。

3.混凝土高度占比系数μ对1 阶自振频率f1有一定的影响，不可忽略，且f1随μ的增加先增大后减小，峰值大概发生在μ ＝0.4。

4.混凝土段与钢塔段截面的壁厚比tc／ts对1阶自振频率f1影响较大，且f1随tc／ts的增加而增加。

5.在实际工程中，锥度θ∈［0，0.025］，此范围内，锥度与对混合结构塔筒的影响较小，因此假定1 合理，且锥度对f1的影响几乎为线性。