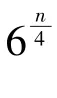最大度至多为3的图上极大分离集的最大数目

李雨欣 苏贵福

(北京化工大学 数理学院,北京 100029)

引 言

若图G中每个顶点的度都为r,则称图G为r-正则图。用Sn、Pn、Cn和Kn分别表示n个顶点的星图、路、圈和完全图,Km,n表示完全二部图,其中二部划分为(X,Y),且|X|=m,|Y|=n。对于两个图G和H,若V(G)∩V(H)=∅,则称G与H不相交。两个不相交的图G和H的并记为G∪H,而nG表示n个G的不交并。

在图G中,若顶点子集S的导出子图的最大度等于0,则称S为图G的一个独立集;若S不为其他独立集的真子集,则称S为一个极大独立集。图中包含顶点个数最多的独立集称为最大独立集。在20世纪60年代Moser等[1]提出如下计数问题:n个顶点的一般图上极大独立集的最大数目是多少?相应的极图又是什么?随后在文献[1]中他们证明了对于n个顶点的图G,其极大独立集个数至多为3n/3个,当n≡0(mod 3)且G为n/3个K3的不交并时达到极值;对于其他的n值,他们也给出了精确的极值并刻画了极图。

此后,学者们聚焦于不同图类上的极大独立集和最大独立集的计数问题的研究,特别是在连通图[2-3]、无三角形的图[4]、二部图[5]、单圈图[6]和最多含有r个圈的图[7]等方面获得重要结果。由于图子结构同社团结构间的关系密切,研究其他图子结构的计数问题也具有重要意义,因此学者们将计数对象扩展得到其他极值结果,如最小支配集[8-9]、极小支配集[10]、最小连通点覆盖[11]、最小反馈点集[12]以及极小反馈点集[13]等图子结构。图子结构的计数问题成为图论和组合数学领域的一个研究热点。

给定图G=(V,E),若顶点子集F在G中的导出子图的最大度至多为1,则称F为图G的一个分离集;若F不为其他分离集的真子集,则称F为一个极大分离集。图中包含顶点个数最多的分离集称为最大分离集。显然图的独立集同时也是其分离集。1981年Yannakakis[14]首次提出分离集的概念,并证明了最大分离集问题在二部图上是NP-困难的。近几十年来,学者们对不同图类上的最大分离集问题的计算复杂性作了深入研究,详见文献[15-16]。

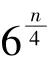
1 相关引理

用MD(G)表示图G中所有极大分离集构成的集合,并记φ(G)=|MD(G)|。

下面的引理1显然成立。

引理1 对于两个不相交的图G和H,有

φ(G∪H)=φ(G)·φ(H)

引理2 设v是任意图G中的顶点,有

若存在顶点w∈N(v)使得N[w]⊆N[v],则

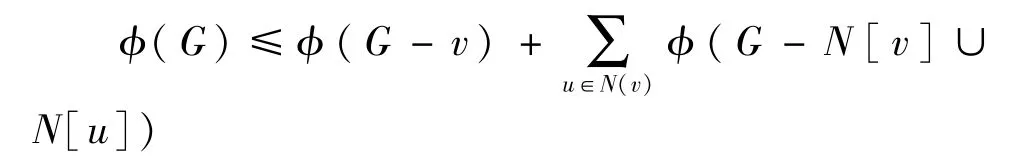
证明:对图G中的极大分离集进行划分,有

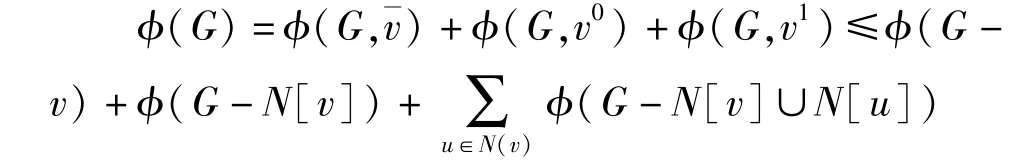
若存在顶点w∈N(v)使得N[w]⊆N[v],则φ(G,v0)=0。因此

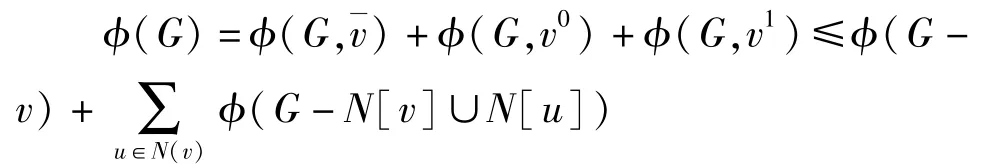
引理3 设v是图G中的一悬挂点,w是其邻点,则

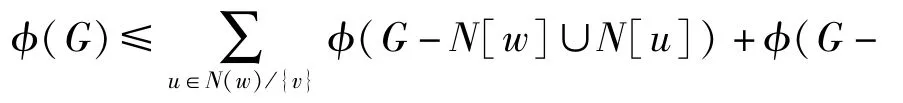
证明:若在图G中存在极大分离集F,使得悬挂点v∈F,则顶点w∈F且dG[F](w)=1。因此

引理4 若图G中有一顶点w恰与两个悬挂点v1和v2相邻,则

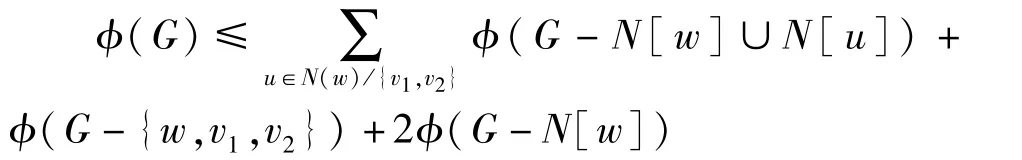
证明:图G中极大分离集所构成的集合可分为以下3类:不包含v1和v2;包含v1和v2;包含v1和w或包含v2和w。因此

引理5 设Pn是含有n个顶点的路,则φ(Pn)＜0.81an。

证明:对顶点数n作归纳。当n≤4时,易验证结论成立。因此,在后续讨论中总假设n≥5,且对任意的Pn-1结论均成立。设顶点v为Pn的悬挂点,w是其邻点,而u是w的另一邻点。由归纳假设及引理3,有

φ(Pn)＜φ(Pn-4)+φ(Pn-2)+φ(Pn-3)＜0.81an-4+0.81an-2+0.81an-3=0.81an(a-2+a-3+a-4)＜0.81an

引理6 设Cn是含有n个顶点的圈,则φ(Cn)≤an,等号成立当且仅当n=4。

证明:当n=3或n=4时,易验证结论成立。因此,后续讨论中假设n≥5。根据引理2和引理5,有

φ(Cn)＜φ(Pn-1)+φ(Pn-3)+2φ(Pn-4)＜0.81an-1+0.81an-3+2×0.81an-4=0.81an(a-1+a-3+2a-4)＜0.81an

2 主要结论及证明

2.1 主要结论

本节研究n个顶点且最大度至多为3的图中极大分离集的最大个数,得到如下主要定理。

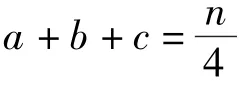
2.2 定理1的证明

对顶点个数n作归纳。当n＜6时,易验证结论成立。因此,在后续讨论中假设n≥6,且对于任意最大度至多为3的n-1阶图结论均成立。

当图G不连通时,设G1和G2是G的两个连通分支,且|V(G)|=|V(G1)|+|V(G2)|=n1+n2。显然G1和G2皆为最大度至多为3的图,根据归纳假设及引理1,有

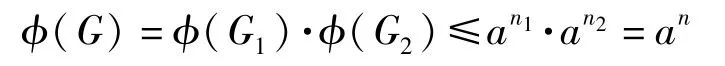
等号成立当且仅当G1和G2同时满足定理中的极图结构,亦即图G满足定理中的极图结构。

接下来考虑图G为连通图的情形。为方便后续证明,给出以下两个断言。

断言1 若连通图G包含悬挂点v,则φ(G)＜an。

证明:记v的邻点为w。由归纳假设及引理4,有

φ(G)≤(d(w)-1)an-d(w)-1+an-2+an-d(w)-1=an(d(w)a-d(w)-1+a-2)

注意到n≥6且Δ≤3,则有d(w)∈{2,3}。经计算可得φ(G)＜an。

断言2 若连通图G中存在顶点u使得N(u)={v,w},且d(w)=3,d(v)=2,则φ(G)＜an。

证明:设N(v)={u,t}。当t=w时,有N[u]⊆N[w],故图G-w≅uv∪(G-{u,v,w})。由归纳假设知

φ(G)≤an-3+2an-4+an-5=an(a-3+2a-4+a-5)＜an

当t≠w时,分以下两种情况讨论。

情况1t∈N(w),N(w)={u,t,s}

当d(t)=2时,图G-w≅P3∪(G-{w,u,v,t}),则由归纳假设知

φ(G)≤3an-4+an-4+3an-5=an(4a-4+3a-5)＜an

当d(t)=3时,如果s∈N(t)且d(s)=2,则V(G)={u,v,w,t,s},易得φ(G)=6＜a5。否则,图G-w包含悬挂点u,且dG-w(t)=2,这就说明图G-N[w]≅v∪(G-{u,v,w,t,s})。因此,有

φ(G-w)≤an-5+an-3+an-4

φ(G)≤φ(G-w)+an-5+3an-5≤an(a-3+a-4+5a-5)＜an

情况2t∉N(w),N(w)={u,s1,s2}

当d(s1)=2且N[s1]={w,s1,s2}⊆N[w]时,图G-w包含悬挂点u,于是由归纳假设得

φ(G-w)≤an-5+an-3+an-4

φ(G)≤φ(G-w)+an-4+2an-5≤an(a-3+2a-4+3a-5)＜an

否则,设A=N(t)-{v,s1,s2}。当A=∅时,图G-w中包含悬挂点u,此时容易发现图G-N[w]≅vt∪(G-{u,v,w,t,s1,s2})。因此

φ(G-w)≤an-5+an-3+an-4

φ(G)≤φ(G-w)+an-6+3an-5≤an(a-3+a-4+4a-5+a-6)＜an

当A≠∅时,有1≤|A|≤2。对于vi∈A,记Bi=N(vi)-{t,s1,s2},其中1≤i≤2。若对于任意Bi都有Bi=∅,则图G-w包含悬挂点u,且

G-N[w]≅P3∪(G-{u,v,w,t,s1,s2,v1})

或

G-N[w]≅S4∪(G-{u,v,w,t,s1,s2,v1,v2})

于是,由归纳假设知

φ(G-w)≤an-5+an-3+an-4

φ(G-N[w])≤max{3an-7,4an-8}=3an-7

φ(G)≤φ(G-w)+φ(G-N[w])+3an-5≤an(a-3+a-4+4a-5+3a-7)＜an

若存在Bi使得Bi≠∅,则图G-w包含悬挂点u,图G-N[w]包含悬挂点v。因此

φ(G-w)≤an-5+an-3+an-4

φ(G-N[w])≤max{an-9+an-7+2an-8,an-8+an-6+an-7,2an-9+an-6+an-8}=an-8+an-6+an-7

φ(G)≤φ(G-w)+φ(G-N[w])+3an-5≤an(a-3+a-4+4a-5+a-6+a-7+a-8)＜an

综上,断言2得证。

由断言1可知,当δ=1时,有φ(G)＜an。由引理6可知,若Δ=δ=2,则φ(G)≤an。因此,接下来只需研究Δ=3且δ=2的图以及3-正则图。

情形ⅠΔ=3且δ=2

在这种情形下,图中必有一个三度顶点v和二度顶点u相邻。设N(u)={v,t},N(v)={u,v1,v2}。由断言2可知,当d(t)=2时,有φ(G)＜an。因此,在后续讨论中总假设d(t)=3。

当t=v1时,有N[u]⊆N[v]。若d(v2)=2且v1～v2,则图V(G)={v,u,v1,v2}且φ(G)=6=a4。否则,图G-v包含悬挂点u,于是由归纳假设得

φ(G-v)≤an-5+an-3+an-4

φ(G)≤φ(G-v)+2an-4+an-5≤an(a-3+3a-4+2a-5)＜an

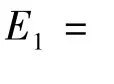
φ(G-v)≤max{an-6+an-4+2an-5,2an-6+an-3+an-5}=2an-6+an-3+an-5

E1≤max{an-6+2an-5,an-5+2an-6,3an-5}=3an-5

φ(G)≤φ(G-v)+an-4+E1≤an(a-3+a-4+4a-5+2a-6)＜an

情形Ⅱ 3-正则图

若G为一n阶3-正则连通图,分两种情况进行讨论。

情况1 图G中不含C3

设v为图G的一个顶点,N(v)={v1,v2,v3}且N(v2)={v,s,t},如图1所示。

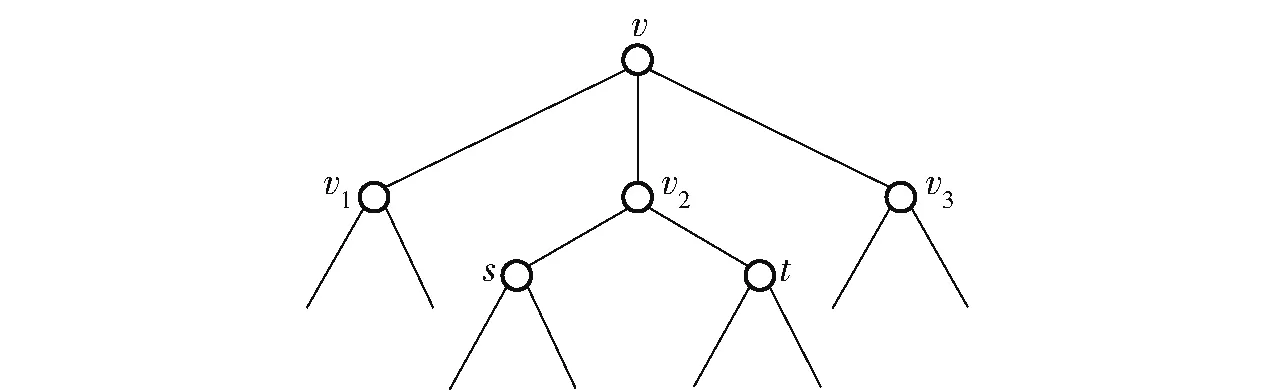
图1 图G中不含C3Fig.1 Case where G doesn't contain C3

若N(s)=N(t)={v1,v2,v3},则G≅K3,3,进而φ(G)=11＜a6。

若N(s)∩{v1,v3}=∅且|N(t)∩N(s)|=3,即图G具有图2所示子结构,由归纳假设有

图2 s不与v1、v3相邻,且s与t有相同邻点Fig.2 Case where s isn't adjacent to v1,v3 and s,t have same neighborhoods

φ(G-v-s)≤2an-7+an-4+an-6

φ(G-v)≤φ(G-v-s)+an-5+an-6+2an-7φ(G)≤φ(G-v)+an-4+3an-6≤an(2a-4+a-5+5a-6+4a-7)＜an

否则,1≤|N(t)∩N(s)|≤2,即图G-v-s具有图3所示的3种子结构之一。根据归纳假设及引理4,有

φ(G-v-s)≤max{an-8+an-5+2an-6,2an-8+an-4+an-6,an-7+an-8+an-4+an-6}=an-7+an-8+an-4+an-6

E2≤max{3an-6,2an-6+an-7,an-6+2an-7}=3an-6

φ(G-v)≤φ(G-v-s)+an-5+E2

φ(G)≤φ(G-v)+an-4+3an-6≤an(2a-4+a-5+7a-6+a-7+a-8)＜an

情况2 图G中包含C3

设v、v1、v2是C3的3个顶点,N(v1)={v,v2,t}且N(v2)={v,v1,s}。

子情况2.1N(v3)∩(N(v1)∪N(v2))={v}(图4)。

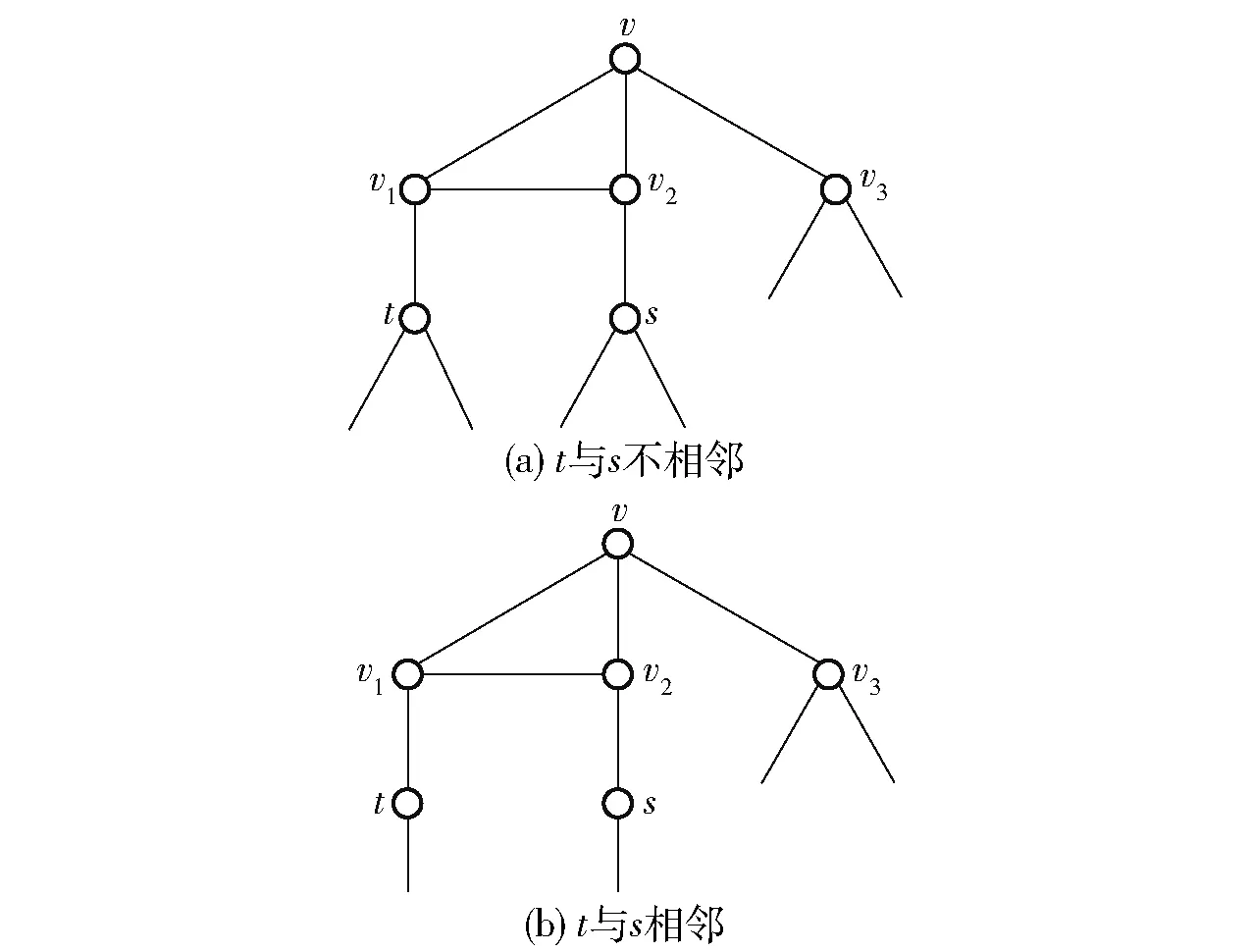
图4 v1,v2,v3有共同邻点vFig.4 Case where v1,v2,v3 have a common neighborhood v

φ(G-v3-v1)≤an-7+an-4+an-5

φ(G-v3)≤φ(G-v3-v1)+an-5+an-6+an-7

φ(G)≤φ(G-v3)+an-4+2an-5+an-6≤an(2a-4+4a-5+2a-6+2a-7)＜an

子情况2.2 图G具有以下两种子结构(图5):

图5 s的邻点分布Fig.5 Neighborhood distribution of s

(1)当t≠v3时,有N(s)={t,v2,v3};

(2)当t=v3时,有N(s)={w,v2,v3}。

因图G-N[s]≅vv1∪(G-N[s]-{v,v1}),则

φ(G)≤an-1+an-6+3an-6=an(a-1+4a-6)＜an

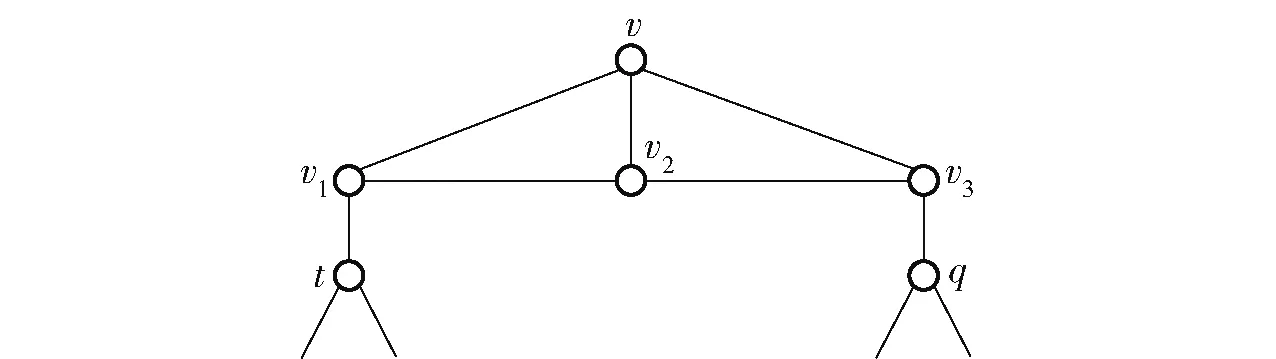
图6 v1,v3有两个公共邻点且非公共邻点不相邻Fig.6 Case where v1,v3 have two common neighborhoods and the different neighborhoods are nonadjacent

注意到在图G-v3中有N[v]⊆N[v1],且图G-v3-v1≅vv2∪(G-{v,v1,v2,v3}),则由归纳假设可得

φ(G-v3)≤an-4+2an-5+an-7

φ(G)≤φ(G-v3)+an-4+2an-5+an-6≤an(2a-4+4a-5+a-6+a-7)＜an

子情况2.4 当v3=t=s时有图G≅K4,直接计算可知φ(G)=6=a4。

综上,定理1得证。

3 结束语