基于功能仿生并联机械腿的全向步行机器人

方跃法，孙天宇

（北京交通大学机械与电子控制工程学院, 北京 100044）

在科技不断进步和装备自动化程度不断发展的今天，机器人行业逐渐成为了当下研究的热门领域.由于需求的不同，机器人的结构种类趋于多样化［1］.其中，移动机器人的应用较为广泛，但是，大多数轮式移动机器人［2］存在无法适应多变地形、狭小空间无法转向等问题，难以适应空间受限和崎岖山路等工况.因此足式全向移动机器人的研究显得尤为重要.

目前国内外众多研究学者针对足式机器人的研究做了大量富有成效的工作.研究多以仿生机械腿为主，其中大部分的仿生机械腿都追求外形仿生，因而采用多关节串联的形式，如Plecnik 等［3］基于stephensonⅠ-Ⅲ型六杆机构设计的足式步行机器人，可根据不同的设计轨迹衍生出不同的设计方案；Zhang 等［4］设计的蝗虫跳跃机器人具有良好的稳定性，能实现直线跳跃；Seok 等［5］设计了一种腿部机构基于三连杆串联的猎豹机器人，奔跑速度可以达到24.12 km/h.虽然功能强大，但串联机构具有承载能力偏低、速度偏慢、运动惯性较大等缺点，所以针对并联移动机器人的研究越来越深入.

并联机构可以将驱动器安装在基座或接近基座的运动副上，因此具有运动惯性小、承载能力高、响应速度快等特点.如Giewont 等［6］设计的Delta-Quad 机器人，具有低惯性和高速度.Air Hopper 机器人［7］可提高驱动加速度，以提供强劲动力.Pan 等［8］设计的六足章鱼机器人具有较高精度和承载能力.王洪波等［9］设计的可重构步行机器椅，既可提高稳定性，又可降低重心.

此外，目前移动机器人转弯功能的实现，多采用差速或臀部转向关节，在转弯过程中需要占用一定的空间.因此，本文设计了一种具有三自由度并联机构腿的足式步行机器人.该机器人的腿部结构应用了多自由度驱动系统，同时采用多耦合闭链结构，相比传统并联机构，结构上更加简单，减少了干涉，增大了可达工作空间且具有2R1T 自由度，实现了全向［10］移动，避免了转弯的复杂步态，解决了空间受限情况下无法移动的问题.

1 机构概述

猎豹的基本运动形式见图1，前肢肩关节能够实现前后摆动和左右张开，如同运动副中的U 副.肘或膝关节可上下弯曲，如同关节R 副，根据动物踝关节是否能够全方位转动，可演变为R 副或S 副，因此动物腿部可以利用URS 或URR 关节串联来代替.为了简化结构，取消踝关节，因此本文采用UR结构来设计并联腿.

整体结构分为驱动系统和被动执行系统.其中，驱动系统通过共用驱动的方法，用3 个电机控制2 个U 副，同时产生2 个输出杆.如图2（a）所示，第一 支 链 由 电 机1 通过转动副R11，R12，R13依次连接L11，L12，L13，第三支链由电机3 通过转动副R31，R32依次连接L31，L13，形成第一U 副，L13作为第一输出杆.同理，第二支链与第三支链可形成第二U 副，L23作为第二输出杆.由图2（b）可知，杆L31，L13，L23形成了一组复合铰链，其连接运动副为R32，R33.

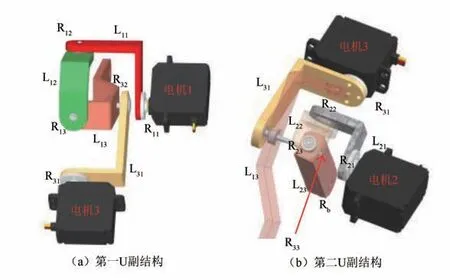
图2 驱动结构拆解图Fig.2 Disassembly diagram of drive structure

被动执行系统由传统的四杆机构组成，将第一、二输出杆作为四杆机构的两驱动杆，可实现类似于猎豹膝关节的R 副，进而设计了一种全新机构如图3所示.图3 中杆La、Lb为四杆机构的被动杆，可通过两驱动杆的控制实现足端任意位置的移动.

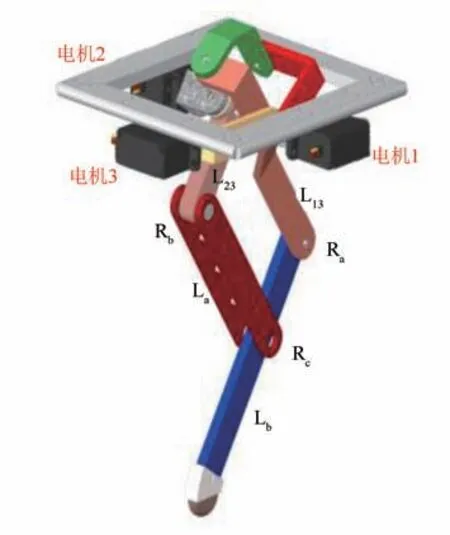
图3 并联机构腿几何模型图Fig.3 Geometric model diagram of parallel leg mechanism

机器人整体三维结构图如图4 所示，移动平台通过螺栓连接多个固定板组成，驱动电机通过电机座与移动平台固连.每个机构腿通过3 个电机控制，共12 个电机且均用联轴器直接与驱动连杆相连.

图4 四足全向步行机器人三维结构图Fig.4 Three-dimensional structure of four-footed omnidirectional walking robot

2 运动学分析

2.1 自由度分析

由于该并联机构含闭链结构，无法直接运用GK 公式进行计算，需引入复合运动副概念，将闭链结构转化为传统机构后计算.图5（a）为机构腿第一、三支链组成的复合运动副机构简图，转化后的传统机构如图5（b）所示.

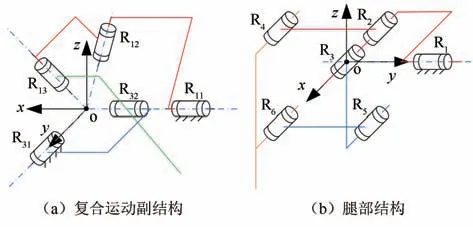
图5 闭链结构转换图Fig.5 Conversion diagram of closed-chain structure

首先，分析复合运动副自由度，以保证简化后机构的运动状态不变.按照图5（a）中坐标系写出支链运动副的运动螺旋系为

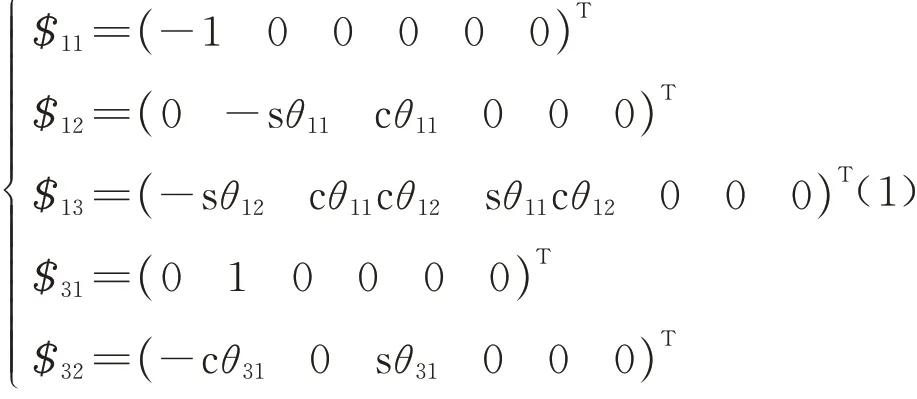
式中：符号c 表示余弦函数；符号s 表示正弦函数；$表示旋量；θ表示角度，旋量和角度的下标表示图5（a）中对应的转动副，根据互易积为0，可得复合运动副的总约束螺旋系为

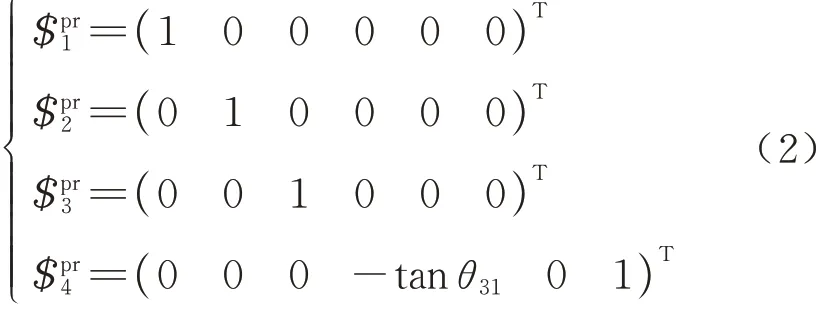
式中：$pr表示复合运动副约束螺旋，其下标表示约束螺旋个数，根据式（2）可知，公共约束λ=3，剩余约束tr=1，不存在线性相关性，其秩kr=1 则冗余约束v=tr-kr=0.代入G-K 公式可得

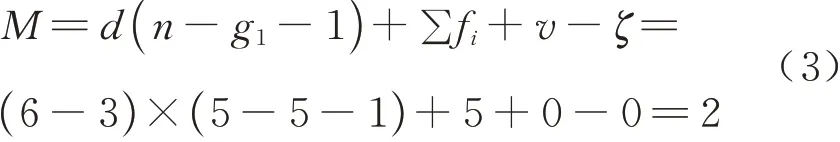
式中：M表示机构自由度；n表示构件数目；g1表示运动副的数目；d为空间机构自由度数；fi表示第i个运动副的自由度数；ζ表示机构中存在的局部自由度.对式（2）求反螺旋，可得复合运动副的总运动螺旋系为

式中：$pm表示复合运动副的运动螺旋，可简化为两转动副串联的形式，如图5（b）中运动副R1、R2所示.同理可得由机构腿第二、三支链组成的复合运动副的总运动螺旋系，简化后如图5（b）中运动副R1、R3所示.按照图5（b）中坐标系可得腿部结构运动副的运动螺旋系为

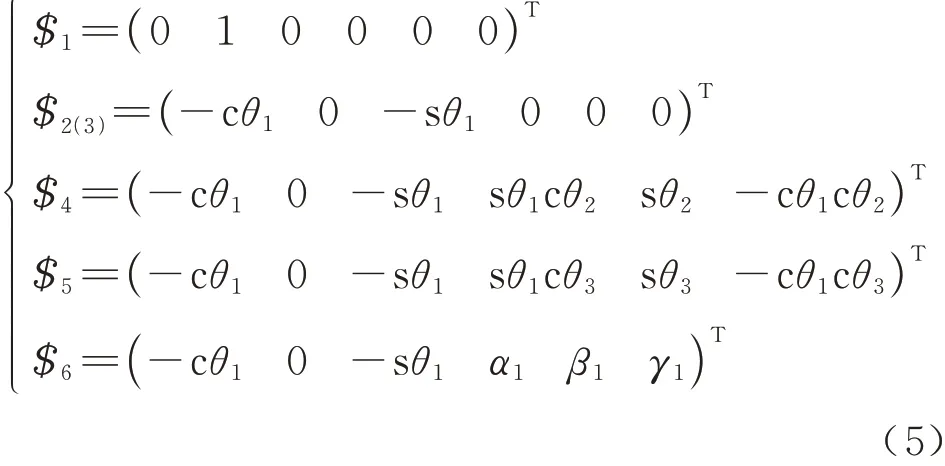
式 中：α1=sθ1（cθ2+cθ3）；β1=sθ2+sθ3；γ1=-cθ1（cθ1+cθ3）.旋量和角度的下标表示图5（b）中对应的转动副，根据互易积为0 可得腿部结构的总约束螺旋系为

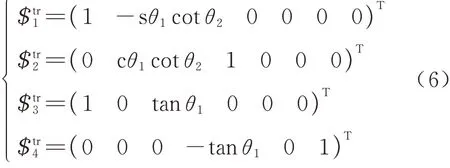
式中：$tr表示腿部结构约束螺旋，其下标表示约束螺旋个数，由式（6）可知，公共约束λ=1，剩余约束tr=3，线性相关且秩kr=2，故冗余约束v=1，由于计算自由度过程中，运动副R1被重复使用了两次，故构件数量n=7，运动副数量g1=7，代入G-K 公式可得

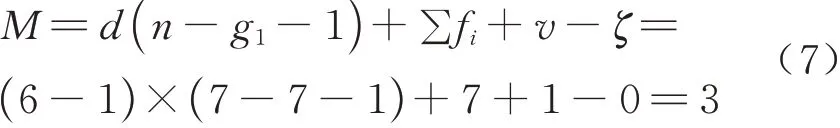
综上所述，并联机构的自由度为2R1T且为RxRyTz.

2.2 运动学逆解分析

绘制机构运动简图，建立如图6 所示左手坐标系运动学模型，图6 中，连接转动副R13与Ra之间的连杆为杆L13，连接转动副Ra与Rc之间的连杆为杆Lc，连接转动副R12与R13之间的连杆为杆L12，连接转动副R23与Rb之间的连杆为杆L23，连接转动副R31与R32之间的连杆为杆L31，转动副R33为复合铰链连接杆L13和杆L23.根据自由度的类型，该机构输出的参数应为2 个姿态参数和1 个位置参数（θx，θy，z）.由于足端不需要考虑姿态的变化，且足端轨迹计算只需末端位置参数P=（x，y，z）即可.参数P与（θx，θy，z）又存在函数关系，所以用（x，y，z）表示运动学参数.计算机构逆解即给定P=（x，y，z），求解驱动关节（θ11，θ21，θ31）的数值，根据几何关系可得P，P1，P2点坐标为

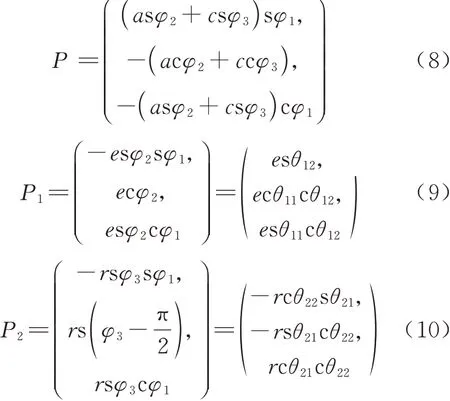
式中：φ1为杆L23与yz平面所成线面角的角度；φ2为杆L13与y轴负方向所成角度；φ3为杆L23与y轴负方向所成角度；P1为转动副R13的位置坐标；P2为转动副R23的位置坐标；a为杆L13上转动副R32与Ra之间长度；c为杆Lc的长度；e为杆L12的局部长度；r为杆L23上转动副R33与R23之间长度；b为杆L31的局部长度；根据结构特征可得出φ3＞φ2，θ角的下角标与图6 中转动副的下角标相对应.

图6 腿部机构结构简图Fig.6 Schematic diagram of leg mechanism

（x，y，z）坐标已知，根据点P位置参数易得

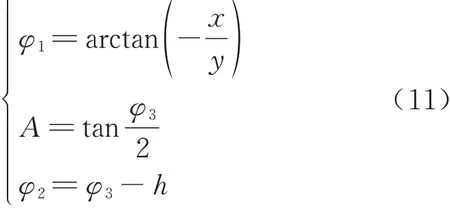
式中

联立式（9）～式（11）可以解出

2.3 运动学正解分析

运动学正解，即已知输入驱动（θ11，θ21，θ31），求解末端的位置参数P=（x，y，z）.由式（8）可知，P 点的位置可用中间参数（φ1，φ2，φ3）表示，故建立（θ11，θ21，θ31）与中间参数（φ1，φ2，φ3）之间的函数关系，再代入到P 点坐标中，正解可得.由式（13）可知

选取两转动副R13和R32的中点连线的中点P3，建立函数关系可得

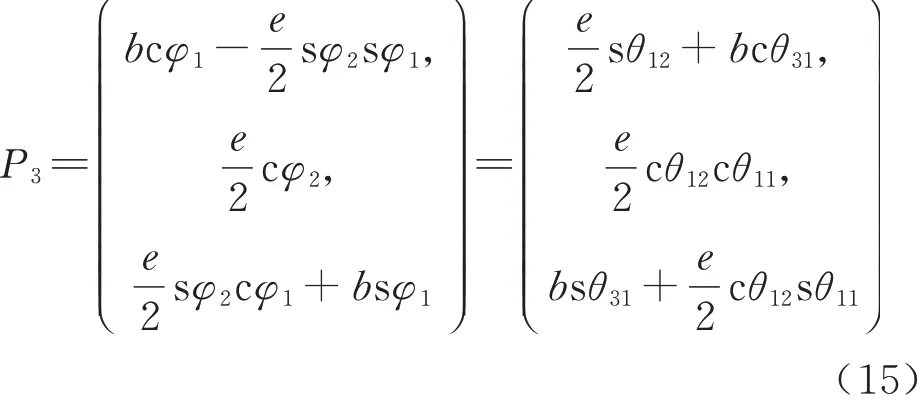
联立式（15）中对应项，求解可得

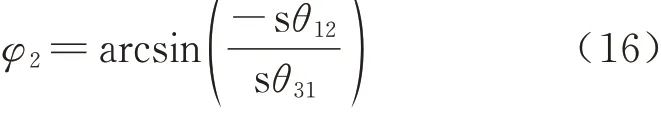
式中：θ12为中间变量，表示转动副R12转动的角度，利用两转动副R13和R32的中点连线的定杆长约束条件，消去中间变量θ12后可得

将式（17）代入到式（16）中可解得φ2，同理可以求得φ3为

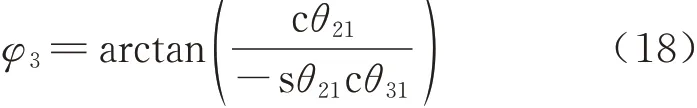
综上所述可得

将式（19）代入到式（8）中可得运动学正解参数.

3 性能分析

3.1 工作空间

机器人工作空间是衡量运动性能的重要指标之一，分为可达工作空间、灵活工作空间、定姿态位置工作空间和定位置姿态工作空间.可达工作空间指末端执行器上某一点所有可达到的点的集合，不需要考虑足端的姿态，所以仅对可达工作空间进行分析.参考桌面型样机尺寸确定参数a=122 mm，c=158 mm，r=16 mm，e=48 mm，b=26.5 mm，采用逆解搜索法，先确定连杆干涉条件，保证Dqi≥D（Dqi表示两相邻杆中心线之间最小距离，D 表示两连杆宽度或直径和的一半），再确定驱动关节变量范围为

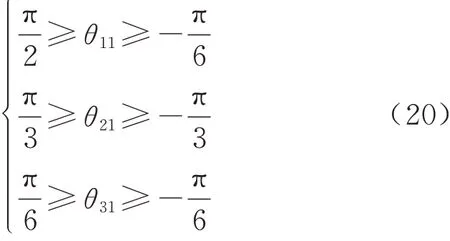
最后选取空间的搜索范围为

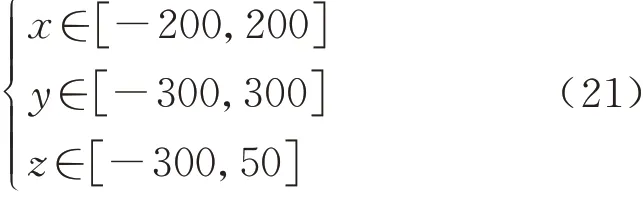
离散化三维空间，依次将点集代入逆解程序，保留符合关节和干涉条件的点集，最终得到点集图如图7 所示.

由Matlab 求解工作空间边界点所围体积为V=9144270.345 7440 mm3，工作空间性能的体积指数［11］表示为

式中：V表示机构工作空间体积；L3vi表示第vi个相关的杆件长度的立方，与本机构相关的杆件长度共2 个，分别为图6 所示的a、c，将相关数据代入式（22）可求得VI=1.587 5.标准化工作空间性能指数NVI，可表示为

式中：VImax为理想最大工作空间体积指数，对于平行四边形结构，其值为定值故根据式（23）计算可得NVI=0.378.而传统的PUMA 机器人的标准指数仅为0.32［11］，由此可知，该机构具有较大的可达工作空间.此外，图7 中工作空间为三维且不同方向的运动相互独立互不影响，可为全向移动提供可行条件，无需规划复杂步态，应用更简单.

3.2 静力学分析

静力学分析的目的是为了计算驱动电机上所受转矩大小以选取合适的电机，如果电机的转矩大小选取不当则无法实现稳定行走，故静力学分析是十分必要的.本文利用虚功原理［12］进行求解.对于机构力学系统来说，应逐个分析并联机构腿各杆件所受的外力.在不忽略任何条件的情况下，对整体系统进行力学模型的建立，则可得方程

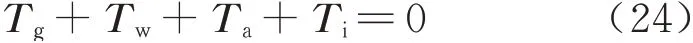
式中：Tg表示重力对广义坐标的影响力矩；Tw表示外力对广义坐标的影响力矩；Ta表示驱动力矩；Ti表示系统惯性力对广义坐标的影响力矩.静力学计算无需考虑惯性力对广义坐标的影响.其中，机器人运动过程中外力的影响是指地面给机构的支撑力.而对于主要采用铝合金材料制成的机器人，根据材料密度2.7 g/cm3以及solidworks 计算所得机构体积可得实际样机重量约为5 kg，假定施加20 kg 负重，共25 kg.双足支撑时支撑力最大为F=25g/2≈125 N，其方向为竖直向上.对于重力矩的计算，每个连杆的重力都对机构产生影响，故均不能忽略.经计算可得，在直角坐标系下的静力学方程为

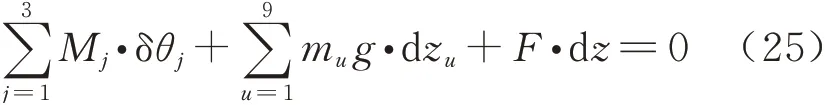
式中：Mj表示第j个驱动力矩；θj表示第j个驱动转角；mu表示第u个连杆的重量；dzu表示第u个连杆的重力在竖直方向上的虚位移；dz表示外力在竖直方向上的虚位移.由于式（25）是在直角坐标系下的静力学方程，所以需要转化成广义坐标方程进行求解.通过运动学正解，建立广义坐标与竖直位移间关系，代入式（25）求导可得

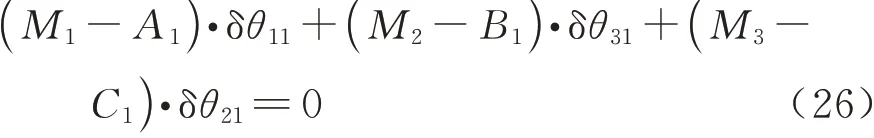
因为虚位移不为0，则根据式（26）可知

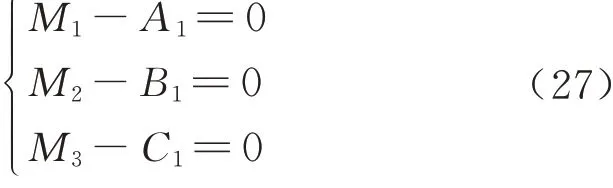
式中：A1，B1，C1是与广义坐标有关的多项式，转矩的大小随广义坐标值的变化而变化.在计算驱动力矩时，给定驱动参数为每条腿最大受力约为125 N，按照给定驱动参数进行仿真所得结果如图8（a）所示.在末端负载125 N 的情况下，驱动力矩最大不超过20 N·m，提高了驱动电机的利用率.故在实际应用过程中，可有效运输一定重量的重物.运用Mathematica 软件进行静力学理论计算所得图像如图8（b）所示.

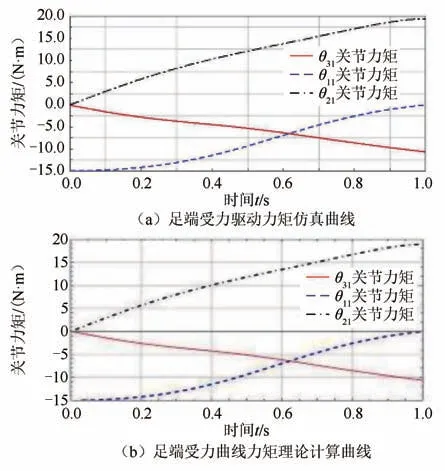
图8 静力学分析图像Fig.8 Static analysis images

由图8 可知，理论值和仿真值曲线几乎完全一致，仿真值与理论计算值结果对比见表1.

由表1 可知，根据计算所得的理论数据值与仿真所得真实数据值几乎完全一致，但仍存在一定误差.产生误差原因主要在于静力学计算忽略了加速度产生的影响，所以计算值必然会产生一定误差.但从结果来看，相对误差最大不超过5%，实际误差不超过0.5 N·m，故可论证计算过程与方法的正确性.

表1 力矩结果对比表Tab.1 Comparison of torque results N·m

4 轨迹规划与步态

4.1 步态分析

四足机器人在行走过程中，腿可分为支撑腿和摆动腿，机器人向前运动的产生是通过支撑腿与地面的静摩擦力来实现的，故支撑腿一定存在.根据支撑腿的个数不同，分为单足支撑步态，双足支撑步态和三足支撑步态3 种［13］，其中双足支撑步态又分为同侧双足支撑步态和异侧双足支撑步态.每一种步态又分3 个阶段：启动阶段，行走阶段和制动阶段.步态的支撑腿越多稳定性越强，三足支撑步态在降低速度的同时提高了稳定性，可用于越障，双足支撑步态虽然牺牲了稳定但提高了速度，可用于平地运输，故需规划三足支撑步态和双足异侧支撑步态两种步态.具体行走步态如图9、图10 所示，红色表示摆动腿，黑色表示支撑腿.

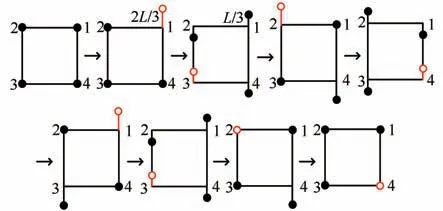
图9 三足支撑步态规划图Fig.9 Gait planning diagram of three-footed support

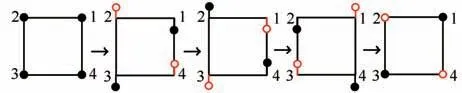
图10 双足异侧支撑步态规划图Fig.10 Gait planning diagram of two-footed support on different sides

三足支撑步态启动阶段为前两阶段，后两个阶段为制动阶段，时间为t1，中间4 个阶段为行走阶段，时间为t2.图9 中摆动和支撑过程中较长步幅为2L/3，足端摆动和支撑过程中较短的步幅为L/3.由于三足支撑的稳定性较强，在工作空间允许的情况下，可选用高度H=50 mm，步长L=90 mm.双足异侧支撑步态相比三足支撑步态较简单，第一阶段为启动阶段，最后一阶段为制动阶段，时间为t1，中间两个阶段为行走阶段，时间为t2.图10 中足端摆动和支撑阶段的步幅均为L.双足支撑的稳定性相对较差，所以选用步态高度和步长时需要考虑减小高度和步长，缩短运动行走时间保证运动稳定性，故选用H=30 mm，步长L=50 mm.

步态规划是为了协调四足行走顺序，使每个腿能有序的行走且连续不间断.除此之外，还需对不同的足端进行轨迹规划，使其按照特定的轨迹移动，实现行走步长和迈步高度.

4.2 轨迹规划

由于本文实现全向运动的理论基础在于可以控制足端落在三维工作空间内的任意位置且各个方向不存在相互干扰现象.对于不同方向的移动，足端轨迹规划的不同之处只是在末端轨迹函数上乘以与方向角相关的系数，故仅对直线方向进行规划.

无论是三足支撑还是双足支撑步态，轨迹规划都需要规划水平和高度2 个方向.因此分别对二者的坐标进行规划，再将其综合起来.以三足支撑直线行走为例，对足端进行轨迹规划.首先规划水平方向轨迹，为保证重心高度不变以提高稳定性，采用倒立摆方法［14］规划，其运动方程为

式中：g表示重力加速度.取初始和结束速度为-15 mm/s 和15 mm/s，初始和结束位置为-30 mm 和30 mm.利用特征方程以及边界条件，求解式（28）可得

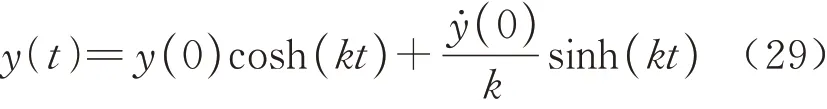
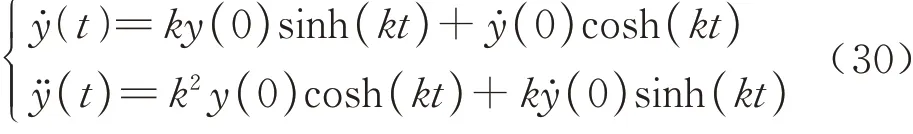
由式（30）可以看出启动阶段速度与加速度为0，会出现卡死现象，需要利用五次多项式规划提供行走阶段的初始速度并保证运动轨迹光滑连续［15］.五次多项式［16］曲线一般形式为

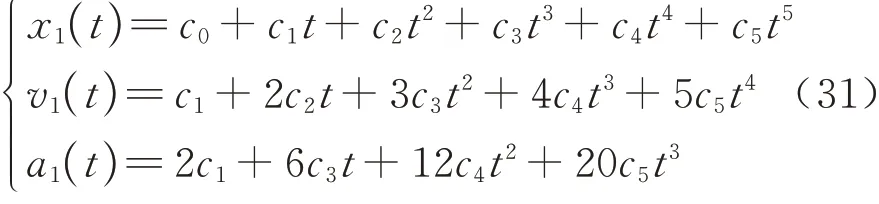
式中：c0、c1、c2、c3、c4、c5分别表示6 个五次多项式待定系数.所以给定初始状态和结束状态的位置xs、xe，速度vs、ve和加速度as、ae6 个边界条件后，可写成矩阵形式为

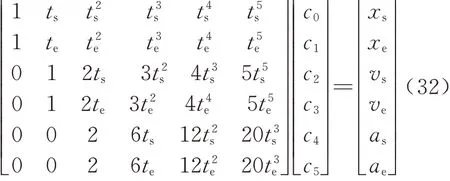
式中：te、ts表示初始时间和结束时间.式（32）中的6×6 阶矩阵为系数矩阵，左乘系数矩阵的逆矩阵，可求得五次多项式系数进而得到规划曲线.

高度方向上，要求轨迹呈先上升后下降趋势，落地时无加速度冲击，故起始和结束位置的速度以及速度的导数均为0.此轨迹速度曲线酷似余弦函数，根据余弦规划可知，速度函数的一般形式为

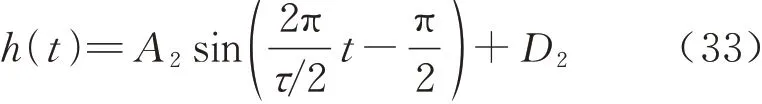
式 中：A2表 示 余 弦 振 幅；D2表 示 余 弦 偏 距，τ表 示余弦函数周期，其中A2=D2，H=50 mm，对速度式（33）进行整理、求导、积分可得余弦规划三曲线为

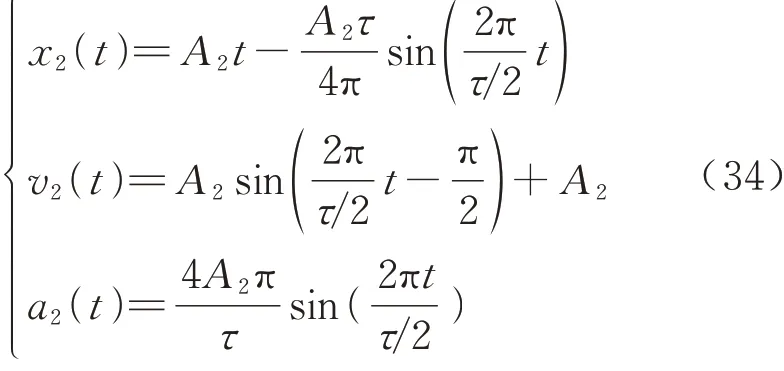
根据图9 所示步态再配合以上足端轨迹规划方法可以得到如图11 所示的4 种主要运动轨迹，根据图11 中轨迹可知，在高度和水平方向上符合设计要求且比例适中.

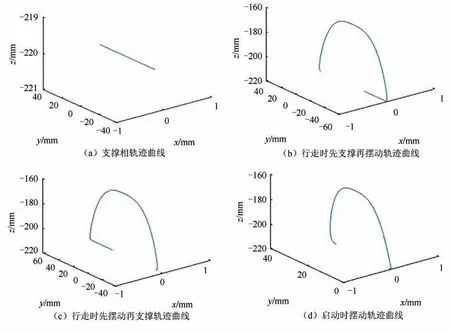
图11 三足支撑步态4 种主要足端轨迹Fig.11 Four main foot trajectories of the gait of three-footed support

5 样机实验

5.1 虚拟样机实验

并联机构腿运动学逆解仿真验证，选取参数为x=0+30t，y=-300+20t，z=-360+30t，得到驱动角度θ11，θ21，θ31随时间变化的理论曲线和仿真曲线对比图，如图12（a）所示.

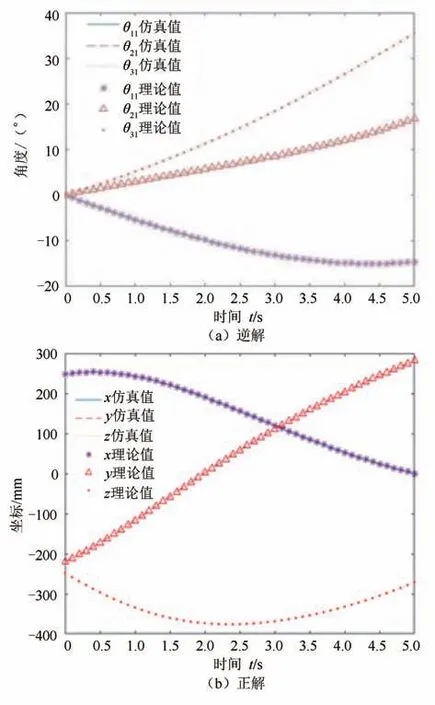
图12 运动学验证曲线图Fig.12 Kinematic verification curves

由图12 可知，由Matlab 计算的理论数据与Adams 导出的仿真真实数据相似度较高，由此可以论证运动学正逆解分析的正确性.

对四足机器人全向行走步态进行仿真，根据轨迹规划结果给定驱动数据，采用CUBSPL 函数作为驱动函数，避免输入产生断点或不连续现象，再利用Adams 的函数单元功能，可得三足支撑步态的全向行走仿真结果如图13 所示.

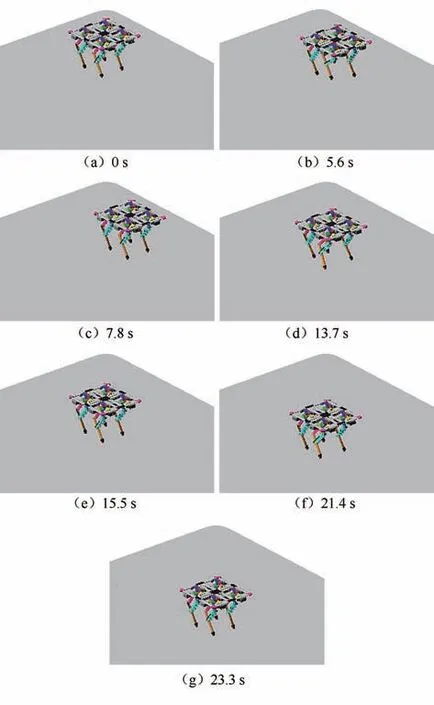
图13 四足步行机器人步态仿真实验图Fig.13 Simulation diagram of gait from four-footed walking robot

由仿真结果可知，四足步行机器人可以实现全向行走，无需特殊的转弯步态，避免了差速转向.而在行走过程中，机构稳定性是表征步态规划可行性的重要指标，可通过行走过程中虚拟样机的质心高度变化曲线来体现，如图14 所示.

由图14 中可知，质心高度的变化范围在43.075～43.45 mm 之间变化，其范围大小不超过0.5 mm 且波动呈周期性变化，说明在行走过程中的稳定性良好.

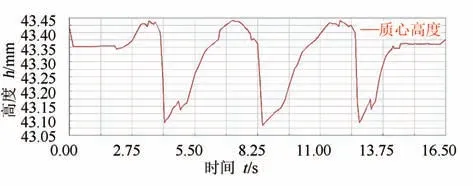
图14 直线行走过程中质心高度变化曲线Fig.14 Height variation curve of the center of mass during straight walking

在轨迹规划过程中所使用的方法，如五次多项式，倒立摆和余弦规划均可以得到连续的加速度，因此避免了因加速度阶跃而产生的刚性冲击或柔性冲击，直线行走加速度变化曲线图如图15 所示.

由图15 中可知，4 个并联机构腿的驱动电机角加速度在运动过程中具有良好的连续性且几乎无突变和断点，其积分的速度曲线仍具有以上特点，说明虚拟样机具有良好的运动性能.

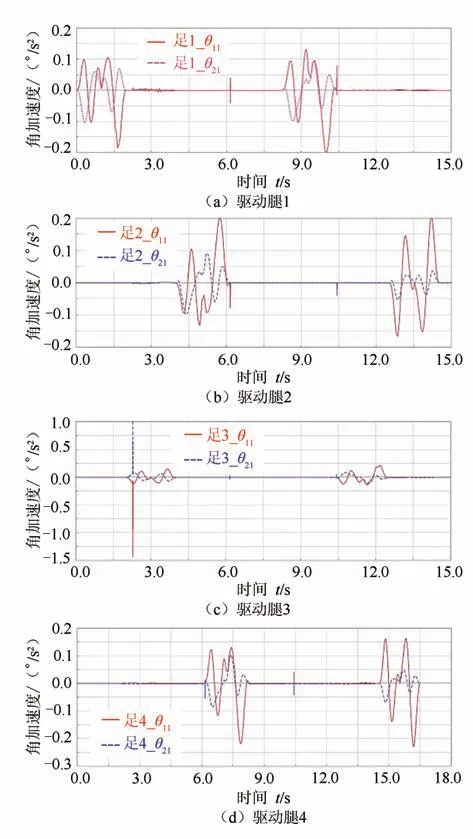
图15 驱动电机加速度变化曲线Fig.15 Acceleration curves of driving motor

5.2 原理样机实验

制作四足全向步行机器人原理样机，进行相关步态实验，验证样机的真实可行性.样机主要由机械杆件，连 接主板，DS3230 舵 机，TTL 串口，供 电模块，控制模块，上位机等部件组成，样机如图16 所示.

图16 原理样机Fig.16 Principle prototype

由于杆件多为弯折形状，应用CNC 金属材料制作较为复杂，故杆件通过3D 打印技术完成，材料选择强度较高的尼龙材料.根据静力学计算力矩，选取电机为DS3230 舵机，通过上位机对舵机控制板发送指令，同时控制舵机实现三种步态的行走如图17所示.

图17 样机行走实验Fig.17 Walking experiment of prototype

图17可知，机器人能够按照理论轨迹行走，实现全方向的全向移动，根据不同的速度需求，可切换两种步态，有效地解决极端空间条件下的变向问题，证实了四足全向步行机器人的可行性.

6 结论

1）设计了一种具有并联机构腿的全向步行机器人.该机器人无需转向关节或差速装置来改变方向，可有效解决空间受限条件下，无法转向的问题.

2）根据运动学逆解，分析了足端位置工作空间.在位置工作空间的范围内，规划了多种行走步态，可实现快速行走和慢速越障等功能.

3）利用Adams 软件对运动学性能和力学性能进行仿真分析，验证了力学计算的正确性并为选取电机提供了理论依据.

4）通过系统模块对舵机进行控制，制作原理样机进行不同步态实验，实现了全向行走的全过程，证明了机构的合理性.