摆线铣开槽加工切削力分析

蔡永林，张祥刚，张正中，席晓琳，王海同

（北京交通大学a.机械与电子控制工程学院,b.载运工具先进制造与测控技术教育部重点实验室，北京 100044）

开槽加工是一种十分常见的工艺，传统的开槽方式一般是采用行切法，逐行逐层去除材料，采用这种加工方式，每一层的第一行切削刀具都满刀切削，受力较大，而且刀具一直参与切削，刀具磨损严重，特别是加工难切削材料时，刀具成本较高，效率较低.摆线铣加工技术是一种在切削过程中对刀具降低负载和充分冷却的加工技术［1-3］，该方法采用循环进刀的方式，每个循环都包括切削过程和非切削过程.应用该技术可以有效地降低加工过程中刀具所受的切削力和切削热，从而提高加工效率，降低刀具成本.近年来该方法被广泛应用在平面开槽和型腔加工中.

摆线铣最早由Elber 等［4］提出，他根据加工的型腔边界构造出对应的中轴线及中轴线上的最大内切圆，通过公切线连接最大内切圆形成位置连续的刀具轨迹，该方法在实际加工中得到了广泛应用［5-6］.而后有很多学者对摆线铣的加工机理进行了研究，Kardes 等［7］对摆线铣削过程中的刀具-工件的接触角进行了建模，并在此基础上进行了摆线铣削的力学和动力学分析［8］.Otkur 等［9］基于相同方法也建立了摆线铣削过程中的刀具-工件的接触角模型，并提出了一种通用的数值算法来预测摆线铣削平面过程的切削力，该算法基于NURBUS 插值拟合的刀位点数据，但是详细的计算过程并没有给出.Zhang 等［10］基于径向切削深度建立了摆线铣开槽的切削力模型，其中摆线铣模型是由圆形摆线，轨迹由圆和直线组成，这种轨迹与一般的摆线轨迹不同.Yan 等［11］也针对圆和直线组成的摆线轨迹建立了开槽的接触角和切削力模型，还进行了加工稳定性的预测，对摆线的步进、主轴转速等参数进行了优化.Wu 等［12］分别利用摆线铣和行切法进行高温镍基合金开槽实验，实验结果表明，与行切法相比，摆线铣加工方法受力更小，刀具磨损更轻微.

综上，目前对于摆线铣加工过程中刀具-工件接触角的建模以及切削力的建模，都只针对稳定铣削过程进行了分析，对于刀具刚切入工件，以及切出工件的过程没有分析，而且对于刀具切出角的计算没有给出详细的计算过程.为了深入研究摆线铣的加工机理，分析摆线铣的加工特点及其所具有的加工优势，本文进行了摆线铣开槽加工过程中切削力的分析，首先建立了摆线铣平面开槽过程中刀具-工件的接触角模型，然后利用微元法建立了切削力模型，并基于该模型比较摆线铣和行切法开槽的切削力，分析摆线铣的优势.

1 摆线铣开槽接触角建模

摆线铣的刀位轨迹见图1，该图建立在o-xy平面上，坐标原点为o，x轴的正方向为进给方向，y轴为工件的宽度方向.摆线的刀心轨迹方程为

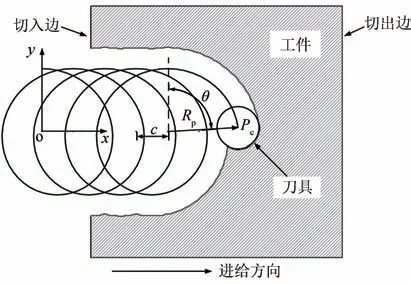
图1 摆线铣开槽刀位轨迹Fig.1 Tool path of trochoidal milling in slotting

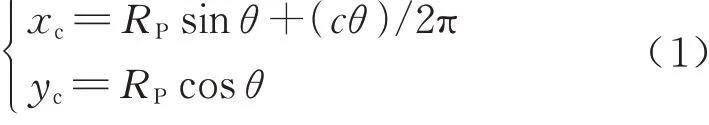
式中：xc和yc是刀心点Pc的坐标；Rp是摆线的循环半径，也就是刀具在任一位置处刀心点和摆线旋转中心的距离；c是步距，代表每前进一个摆线循环，摆线旋转中心前进的距离；θ是刀心转角，即刀心点与摆线旋转中心的连线和y轴正方向的夹角，θ是一个累积量，每前进一个摆线循环增加2π.

已知刀具半径Rc，则由式（1）可得刀具上任意一点的坐标满足

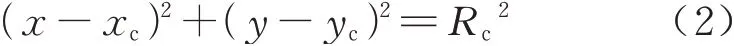
整个开槽的过程从刀具与工件接触开始，到刀具完整的从切出边切出为止.摆线铣开槽过程中，一刀位点处刀具和工件接触的示意见图2，图2 中，P1点为切入点，P2为切出点.P1点和P2点之间的区域就是刀具-工件的接触区域，在该区域内的刀刃都会参与切削.沿顺时针方向，P1和P2点与刀心Pc的连线和y轴正方向的夹角分别为切入角ϕst和切出角ϕex.在这个二维平面内，只要刀具上某一点和刀心Pc的连线与y轴正方向的夹角在切入角和切出角之间，则该点肯定参与切削，切入角和切出角之差便是接触角ϕ，即

由图2 可知，只需计算切入点和切出点的坐标即可得到切入角、切出角以及接触角的值.本文将整个摆线铣开槽分成了切入、稳定切削和切出3 个部分.下面分别对这3 个部分进行刀具-工件接触角的求取.线中心最远点Pmax在切入边外时，以及该点在切入边内时.Pmax点的坐标为

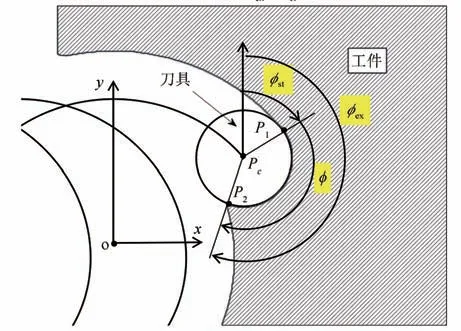
图2 摆线铣槽接触角示意图Fig.2 Contact angle diagram of trochoidal milling groove

1.1 切入部分

切入部分是摆线铣切削的第一个循环，从刀具接触工件开始，直到第一个摆线循环结束.因为摆线铣第一个切削循环，切入、切出角的计算和工件的切入边坐标有关，所以将其和其他部分区别开.为了避免满刀切削，在切入部分刀具整体不会都进入工件内部，所以刀具总会与切入边有交点.将该过程分为两种情况，如图3 所示，分别是刀具上距离摆

当Pmax在切入边外时，切入点P1和切出点P2均为刀具和工件切入边的交点，可知P1点和P2点的x坐标值均满足

式中：d为切入边和坐标原点在进给方向的距离.联立式（2）和式（5）可以得到两个解，y值较大的是P1点，y值较小的是P2点.

当Pmax在切入边内时，此时点Pmax是切入点，由式（1）和式（4）可以求出该点的坐标，直至刀具与工件脱离，Pmax点一直都是切入点，由Pmax点的定义可以得出，摆线循环切除材料所留下的边界就是Pmax所经过的轨迹，也就是刀具上距摆线中心最远点的轨迹.此时切出点P2与图3（a）中的切出点一样，是刀具和工件切入边的交点.当Pmax点的x坐标值小于d时，刀具就与工件脱离，进入了非切削状态.直至刀心转角大于2π，则第一个摆线循环结束，进入稳定切削部分.

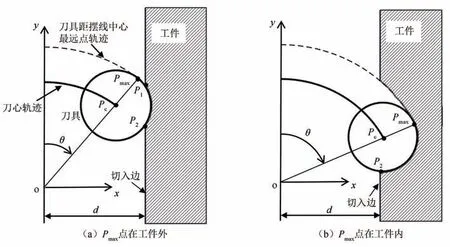
图3 摆线铣切入部分两种切削状态Fig.3 Two cutting states of trochoidal milling cut-in part

1.2 稳定切削部分

当摆线铣进入稳定切削之后，刀具的切削状态如图4 所示，切入点为刀具上距离摆线中心最远点Pmax，切出点为P2点，该过程直至刀具开始从切出边切出为止.

当摆线铣进入稳定切削状态，此时接触角的求取要考虑上一条刀轨所切除的区域.此时切入点为Pmax，切出点为刀具与上一个摆线循环切削后留下边界的交点，即图中的P2点，上一个摆线循环切削留下的边界就是上一个循环刀具上Pmax点所走过的轨迹.由图4 可知，此时交点P2和P2′是刀具上的点，所以其坐标满足式（2），又知P2和P2′为上一个摆线循环刀具上Pmax点所走过的轨迹，所以联立式（2）和式（4），可得

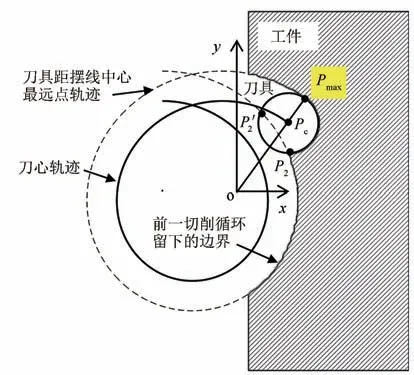
图4 稳定切削部分刀具切削状态Fig.4 Tool cutting state of stable cutting part

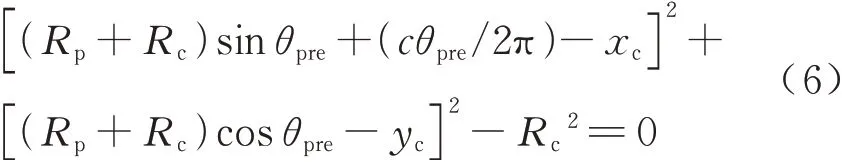
式中：θpre为上一个摆线循环的刀心转角，因为式（6）是带有三角函数的非线性方程，所以无法用解析方法解出，只能考虑用数值方法求出近似解.如果不限制θpre的取值区间，式（6）有无数个解，所以首先要确定θpre的取值区间.根据刀具此刻的刀心转角θnow可以求出当下摆线的循环次数N为

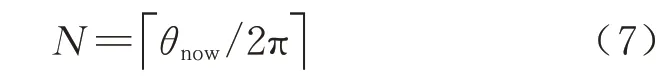
当前刀具的转角区间必满足

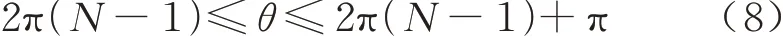
所以可得θpre满足

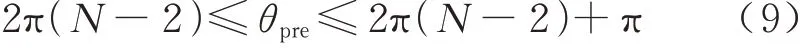
在该区间内，θpre只有两个解，分别对应着P2和P2′点的刀心转角，所以要对该区间进行进一步的缩小.将式（6）写成函数形式为

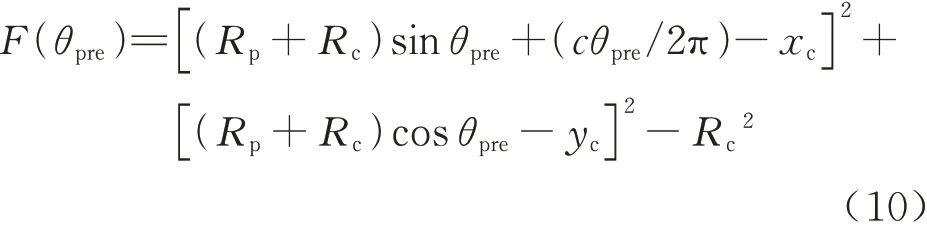
对其求导，可得其一阶导函数

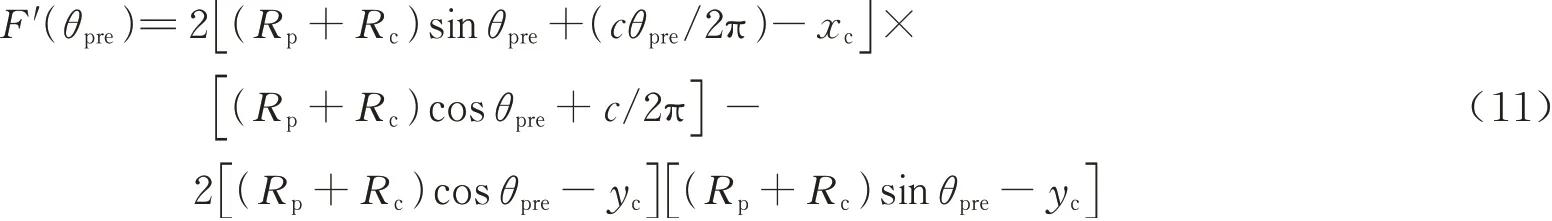
F(θpre)和F′(θpre)在区间[θst，θend]内的图像如图5 所示，其中

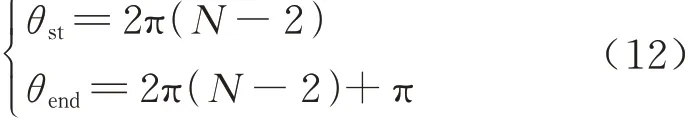
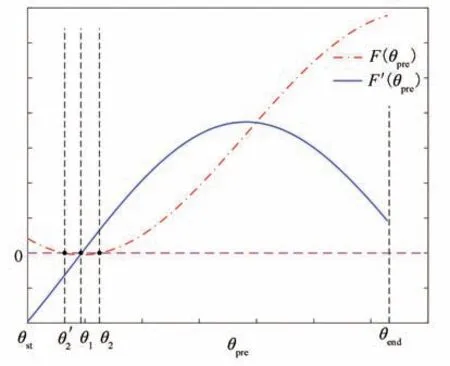
图5 F(θpre)和F′(θpre)图像Fig.5 Images of F(θpre)and F′(θpre)

F(θpre)在该区间内一共有两个零点，分别出现在θpre=θ2和θpre=θ2′两 个 点 处，结 合 图4 可 知，P2点对应的刀心转角为θ2，P2′点对应的刀心转角为θ2′点，要求的是θ2的值.

通过观察F(θpre)的图像可知，该函数图像在该区间内先减后增，其导函数为0 的点必定出现在两个零点之间.通过观察F′(θpre)的图像可知θpre=θ1时F′(θpre)=0，所以θ2∈[θ1，θend].又因为F′(θpre)在该区间内仅有一个零点，所以可以采用二分法得到θ1的值.二分法的算法如下：

1）给定初始的精确度δ以及初始区间[θst，θend].

2）令θ1=(θst+θend)/2，并计算F′(θ1)的值.

3）若F′(θ1)＜0，则令θst=θ1，若F′(θ1)＞0，则令θend=θ1，返回2）重新执行.若F′(θ1)=0 或|θstθend|＜δ，则输出θ1的值作为最后的结果.

求出θ1后，便得到了θ2所在的区间，在该区间内F(θpre)仅有θpre=θ2这一个零点，在该区间内使用二分法求出θ2的近似值，从而求出切出点P2的坐标.

1.3 切出部分

当刀具从切出边切出，如图6 所示，此时切入点为刀具与切出边的交点，从而可得

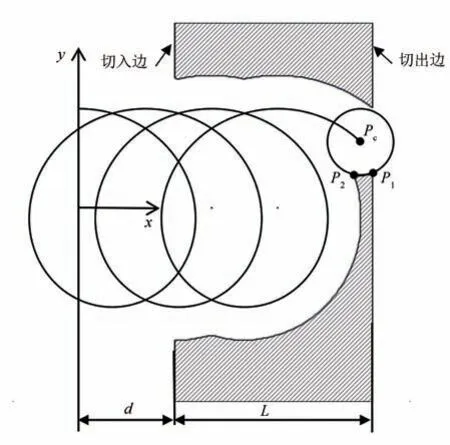
图6 摆线铣开槽切出状态Fig.6 Cut-out status of tochoidal milling in slotting

式中：L是工件的长度，由式（2）和式（13）便可以求出P1点的坐标.切出点与稳定切削部分相同，都是刀具和上一个摆线循环刀具包络线的交点，计算方法与稳定切削部分的切出点计算方法相同.

利用以上所述算法可以求出摆线铣开槽过程中任一时刻刀具-工件的切入角、切出角以及接触角.

1.4 行切法开槽接触角建模

为了分析摆线铣与行切法相比的优劣，对行切法在开槽过程中刀具-工件的接触角进行分析.在行切法开槽过程中，刀具主要有两种切削状态，第一行切削时刀具为满刀切削，如图7（a）所示，在该状态下刀具的切入点P1在刀心Pc点的正上方，所以此刻的切入角ϕst=0.切出点P2在刀心Pc点的正下方，所以此刻的切出角ϕex=180°，从而可得ϕ=ϕex=180°.

当刀具完成第一行切削之后便进入第二种切削状态，如图7（b）所示，在这种情况下刀具的接触角和切削行距dr有关，由图中的几何关系，可以得出接触角ϕ的大小为

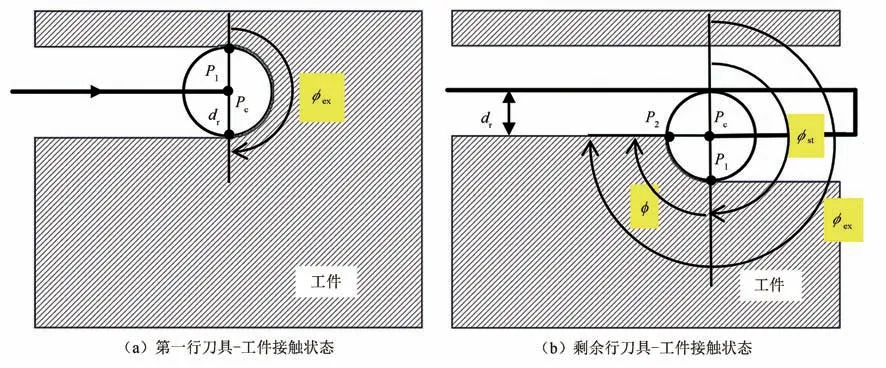
图7 行切法开槽刀具-工件接触状态Fig.7 Contact state of slotting tool-workpiece with row cutting method

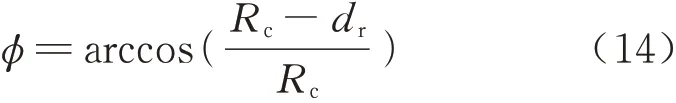
式中：dr为切削行距，也是径向切深.刀具沿直线走刀时，切入角的大小ϕst始终保持不变，一直为180°，从而可得切出角为

1.5 接触角对比分析

利用Visual Studio 软件，将计算摆线铣和行切法开槽接触角的算法使用C++语言进行了实现.为了验证算法的正确性，以及对比摆线铣和行切法在开槽过程中接触角的不同，设计了一组对比分析.利用上述算法分别模拟摆线铣和行切法加工一个尺寸为40 mm×40 mm 的平面槽.令两种铣削方式在相同的时间内铣完该槽，比较二者的接触角大小.摆线铣和行切法的切削参数如表1 所示.

表1 切削参数Tab.1 Cutting parameters

通过执行程序进行了模拟，所得的分析结果如图8 所示.如图8 可知，摆线铣过程中刀具-工件接触角呈现周期性的变化，每个摆线循环为一个周期，每个周期都有两个部分，切削部分和非切削部分，在非切削部分刀具和工件不接触，所以接触角一直为0，在切削部分接触角从0 一直增加到最大值，然后再逐步减小.在摆线第一个循环，接触角的最大值与变化情况都和稳定切削状态不同，因为此刻刀具接触角的大小和切入边有关，在稳定切削部分，每个循环接触角的变化情况都是相同的，在切出部分，因为刀具可能在切削中途切出工件，所以可能出现接触角突然变小，或者变为0 的情况.对于行切法，接触角只有两个固定的值，在第一行切削时，接触角是180°，在其他情况下一直维持在66.4°.

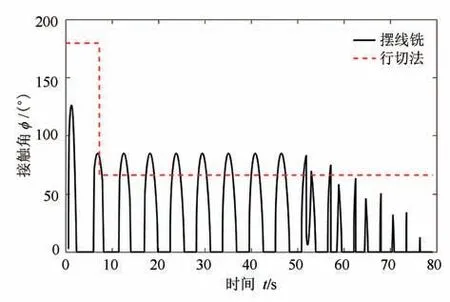
图8 摆线铣和行切法开槽刀具-工件接触角Fig.8 Slotting tool-workpiece contact angle using trochoidal milling and row cutting

通过对比，在整个切削过程中，摆线铣的接触角只在几个峰值位置比行切法稍大，其他大部分情况要比行切法小.两种方法切完整个槽的时间都是79.2 s，其中有62.95 s 的时间，行切法的接触角要大于摆线方法，而且摆线铣接触角平均值为40.586 7°，仅为行切法的57.4%.

2 摆线铣开槽切削力建模

2.1 微元法切削力建模

采用微元法进行立铣刀切削力建模的原理是将刀具切削刃沿轴线方向划分为有限个切削微元，则每个切削微元都相当于在进行一个斜角切削过程，然后根据斜角切削理论，求出每个切削微元所受的微元切削力，最后将所有参与切削的微元所受的切削力叠加便可以求出刀具所受的总的切削力.

首先将刀具切削刃沿轴线方向，等分成有限个切削微元，每个切削微元的高度为ΔZ，则高度为z的微元在圆周方向相对于y轴正方向的转角为

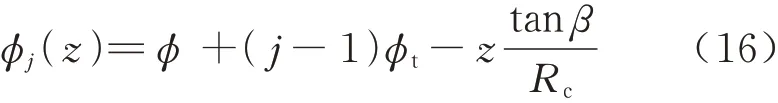
式中：β为刀具的螺旋角；j=1，2，…，N为刀齿代号；ϕ为1 号刀齿在z=0 处与y轴正方向的夹角；ϕt为刀具的齿间角.

在接触角建模过程中已求出了刀具在切削过程中的切出角和切入角，当ϕj(z)在切入角和切出角之间便可以认为该切削微元参与切削，即

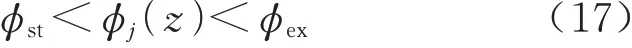
利用式（17）便可以求出所有参与切削的微元，每个切削微元都相当于在进行一个斜角切削过程.目前对于斜角切削过程切削力的求取已经有了很成熟的办法［13］，微元切削力大小可以用切削力系数和切屑横截面面积的乘积计算得到，即3 个方向的微元切削力满足

式中：dFr，j(ϕ，z)、dFa，j(ϕ，z)和dFt，j(ϕ，z)分别为第j个刀齿上高度为z处的微元所受的径向、切向和轴向切削力；dz为该微元轴向的高度；Kie、Kic(i=a，r，t)为两组与刀具几何结构以及材料有关的切削力系数，需通过实验确定.hj(ϕ，z)表示未变形切屑厚度，在数值上等于已加工表面和刀齿下一刀即将加工出的表面的径向距离，即

式中：ft为每齿进给量.已知主轴转速ns和进给率f，则

因为摆线铣的刀具路径不是直线，所以不同于直线进给方式，摆线铣的瞬时进给方向沿着刀心轨迹的切线方向.已知摆线循环转速为np，则

式中：ω是摆线循环的瞬时角速度，所以由几何关系可知

由式（16）～式（22），在给定切削参数的前提下，便可以求出任意一个切削微元所受的微元力，但是因为所求出的是切向、轴向和径向3 个方向的力，在每个微元处切向和径向方向是不同的，因此无法直接叠加，所以需要将微元力转换为x，y，z3 个方向的力来进行叠加，可通过以下公式进行转换

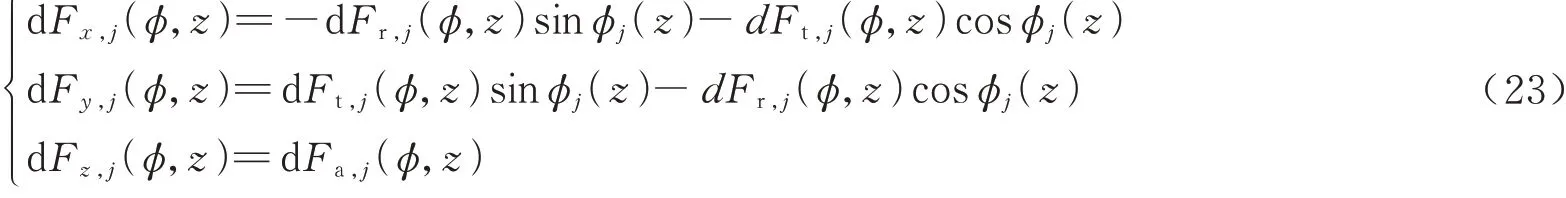
对所有切削微元所受的切削力求和，便可以得 出刀具在3 个方向所受的总切削力，即

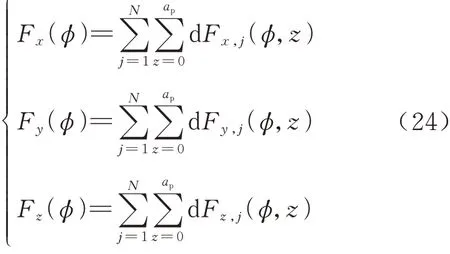
式中：ap为轴向切深.

2.2 切削力系数识别实验

为了获取切削力系数，本文采用Budak 等［14］提出的方法进行切削力系数的识别，设计了10 组铣槽实验，每组的实验参数如表2 所示.实验所用的机床为科德数控生产的KMC-400SU 五轴数控加工中心，测力仪为Kistler 生产的9129AA 型测力仪，所用的刀具为SAT 的S-400 系列的三刃铝用立铣刀，刀具材料为硬质合金，直径5 mm，螺旋角45°.实验所用的材料为7075 铝合金.

表2 实验参数Tab.2 Experimental parameters

搭建的实验平台如图9 所示.实验时，刀具铣削工件，测力仪实时收集铣削产生的切削力信号，采集的信号经过数据处理设备的处理之后传输至计算机中.在计算机中，安装DynoWare 数据分析软件，利用该软件可以实时观察采集的切削力信号，实验过程中将测力仪的采样频率设置为1 500 Hz.实验过程及加工的结果如图10 所示.

图9 切削力识别实验平台Fig.9 Experimental platform for cutting force identification

图10 切削力识别实验过程Fig.10 Experimental process of cutting force identification

采用第1 组实验参数采集到的切削力数据如图11 所示，其他组的数据不再列出.进行切削力系数识别需要得到每组实验的平均切削力，将每组实验所有采样点的切削力数值进行求和，然后取平均，便可得到每组实验的平均切削力，结果见表3.

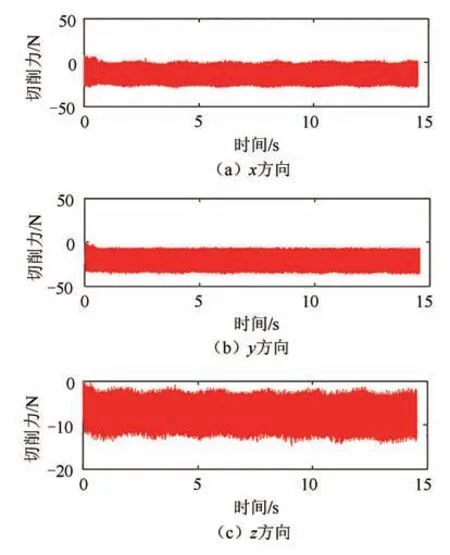
图11 第1 组参数实验结果Fig.11 Experimental results of the first set of parameters

采用Budak［14］的方法对实验数据进行处理，得到的切削力系数为

为了验证该模型的正确性，利用建立的模型采用与表3 相同的参数进行模拟，与实验所得的结果对比如图12 所示.在x方向上预测的数据与实验数据最大偏差为3.85%，平均偏差为2.69%；y方向最大偏差为9.8%，平均偏差为2.78%；z方向最大偏差为2.29%，平均偏差为1.34%，所以利用切削力模型预测得到的数据和实验所得数据相差很小，完全可以认为该模型的计算结果是有效的.

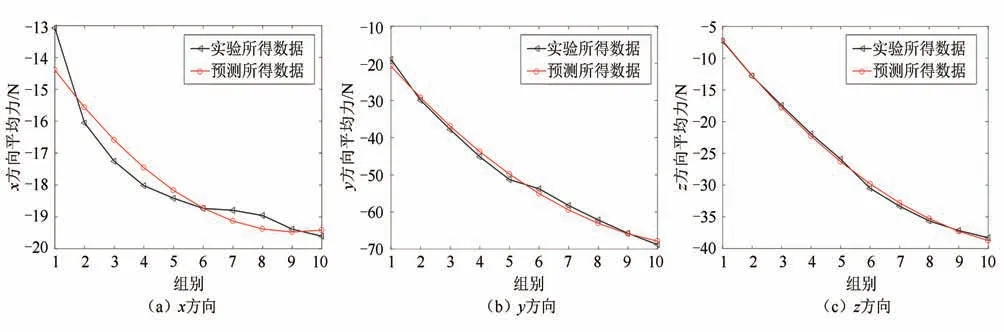
图12 预测与实验结果对比Fig.12 Comparison of experimental and predicted results

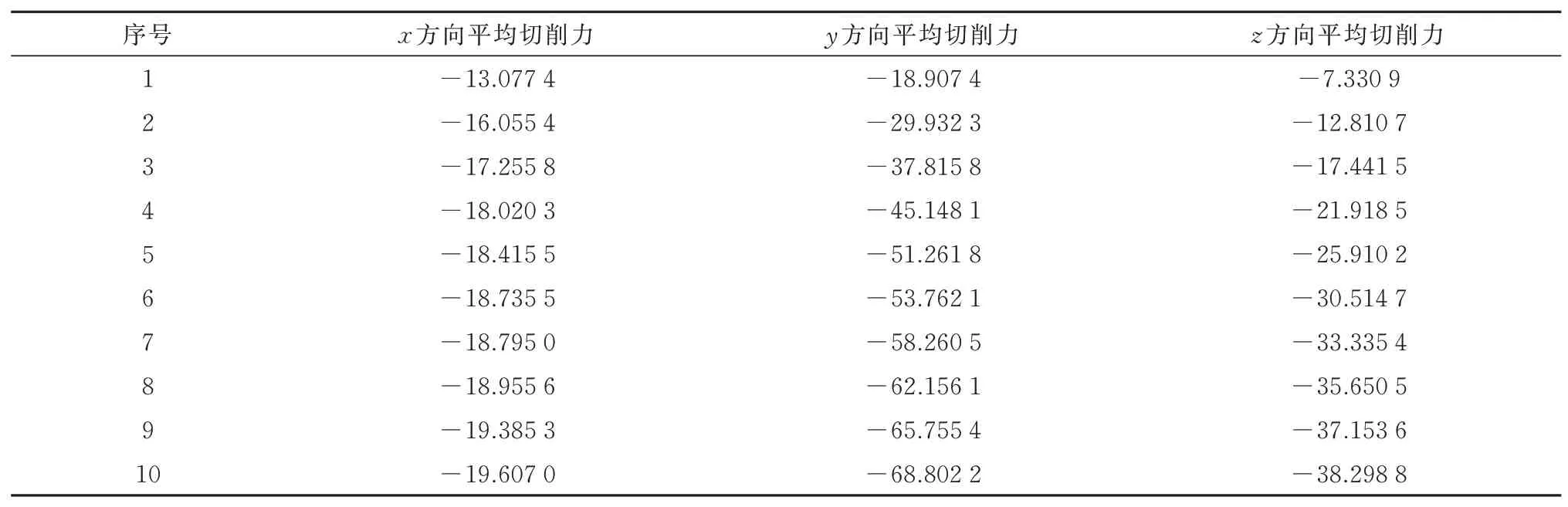
表3 实验所得平均切削力Tab.3 Average cutting force results from experiments N

2.3 切削力对比分析

为了对比摆线铣和普通行切法相比的优势，利用本文建立的切削力模型进行了分析，分别使用摆线铣和普通行切法在平面上加工相同尺寸的槽，分析加工过程中的切削力变化情况. 槽的尺寸为40 mm×40 mm×2.5 mm，两种方法使用相同的刀具，刀具半径为2.5 mm，在相同的时间内完成加工.因为摆线铣在非切削阶段刀具与工件不接触，所以在非切削部分摆线铣采用更高的进给速度.切削参数见表4.

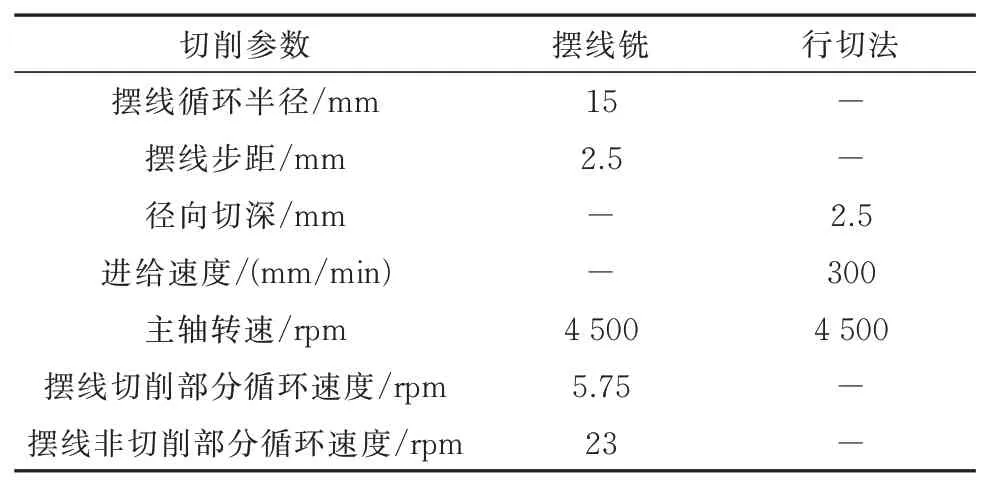
表4 切削参数Tab.4 Cutting parameters

由于无法确定刀具在任意时刻的转角，即式（16）中的ϕ值，也就无法确定切削微元的切入角以及切出角，所以本文采用取平均的方法，在0°～360°之间以0.001°为间隔取值作为刀具在某一位置处的ϕ值，针对每一个ϕ值均可以求出一个切削力，将所有值取平均作为当前时刻刀具所受的切削力，结果如图13所示.

由图13 可知，切削力的变化情况和接触角大致相同，普通铣削在加工过程中接触角只经历一次变化，所以切削力也就稳定在两个固定值.摆线铣因为刀具-工件的接触角一直在变化，所以切削力的变化情况和接触角的变化情况相似，也是呈现规律的波动，在非切削部分刀具各个方向所受的切削力为0.摆线铣和行切法各个方向的平均切削力如表5所示.

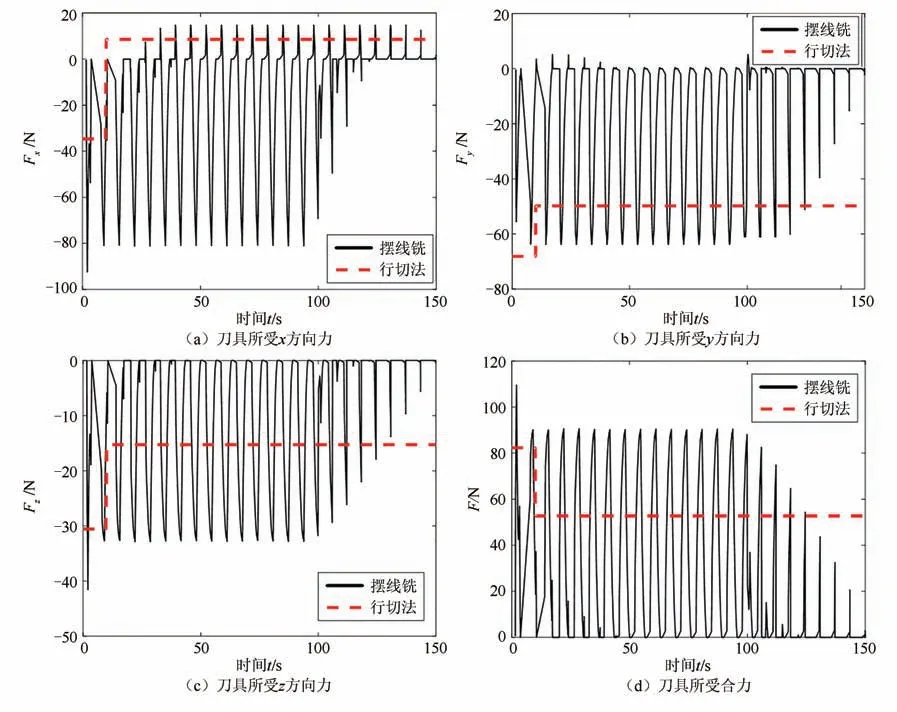
图13 切削力对比仿真实验结果Fig.13 Simulation results of cutting force comparison

由表5 可知，摆线铣在x方向的平均切削力大于行切法，在y、z方向的切削力以及合力比普通铣小，因为进给方向的不同，所以两种方法在x，y轴上的切削力占比不同，对比意义不大，对比合力更有意义，摆线铣合力的平均值为行切法的44.2%.所以使用摆线铣方式进行开槽加工，可以减小切削过程中刀具所受的切削力，使加工过程更为平稳，减少刀具和工件的震动，从而在提高刀具寿命的同时得到更好的表面质量以及更高的加工精度.

表5 实验所得平均切削力Tab.5 Average cutting force results from experiments N

2）利用微元法建立了立铣刀切削力模型，并验证了切削力模型的正确性.通过理论分析对比摆线铣和行切法在效率、主轴转速、切深相同的条件下，开槽过程的刀具受力情况.结果表明摆线铣在切削过程中刀具整体所受的平均切削力为行切法的44.2%.

3）在开槽过程中采用摆线铣加工方式，刀具和工件的平均接触角以及刀具所受的切削力都要明显小于行切法.因此使用摆线铣方式，加工过程更为稳定，刀具寿命更长，从而可以采用更高的进给和更大的切深来提高加工效率.

3 结论

1）建立了摆线铣开槽过程中刀具-工件接触角的模型，提出了一种求取摆线铣加工过程中刀具的切出点坐标的数值解法.根据所建立的模型，设计了对比分析，通过分析可得，在整个切削过程中，摆线铣削方式的接触角平均值仅为行切法的57.4%，而且在79.5%的时间内接触角小于行切法.这表明在整个切削过程中摆线铣刀具的切削状态大部分时间要优于行切法，且摆线铣更有利于排屑以及刀具的降温.