转向架斜楔摩擦特性研究

2022-07-14李玉龙吕大立1c吕可维张琪昌刘嘉兴

北京交通大学学报 2022年3期

李玉龙，吕大立，1c，吕可维，张琪昌，刘嘉兴

（1.天津大学a.机械工程学院，b.天津市非线性动力学与控制重点实验室，c.内燃机研究所，天津 300072；2.中车齐齐哈尔车辆有限公司大连研发中心，辽宁大连 116042）

铁路运输作为最重要的交通方式，在各国经济发展中发挥了十分重要的作用.铁路运输重载、高速一直是各国追求的目标，目前美国大部分铁路货车轴重达30 t 以上，俄罗斯和欧洲货车轴重在25 t 左右.速度方面，北美快运货车运行速度达120 km/h，欧洲普遍达到120～160 km/h［1-3］.我国通用货车轴重也已提高到27 t，并且已研制出时速160 km/h 的快运货车.斜楔减振器作为转向架中的核心部件，其运行平稳性，良好的摩擦性能是保证车辆动力学性能的基本条件，因此斜楔减振器摩擦板摩擦特性的研究，对于重载铁路货车提速技术是必不可少的.

早期由于列车运行速度的提升，部分转向架出现摩擦板磨损严重的问题，摩擦板耐磨性成为制约列车提速的重要因素，科研人员针对摩擦板的耐磨性开展了相关研究.陈秀娣等［4］在环行道台架疲劳实验台上测定各摩擦材料的耐磨性能，指出改进热处理工艺可显著提高摩擦板耐磨性.王泽华等［5］进行大量摩擦磨损性能比较试验，指出等温淬火球铁斜楔和衬套具有比传统材料高得多的耐磨性.Cyxob 等［6-7］对合金灰铸铁材质的摩擦斜楔和25X号钢材质的磨耗板进行试验台试验和走行试验，结果表明上述材料制成的摩擦斜楔和磨耗板具有更高的耐磨性.

随着重载列车提速技术的进一步发展，科研人员发现转向架悬架性能对摩擦系数的变化非常敏感，斜楔减振器摩擦系数的大小及稳定性在很大程度上决定了列车的动力学性能［8-11］，众多研究开始关注斜楔减振器摩擦材料摩擦系数的稳定性及其影响因素.西方各国自九十年代开始相继在摩擦板上应用新型聚合物材料以保证斜楔摩擦性能的稳定性［12-13］.我国赵海鹰等［14］研制了新型高分子复合材斜楔摩擦板，并通过模拟工况台架实验和实际运用实验研究了其摩擦磨损性能和可靠性.韩建民等［15-17］对3 种斜楔材料的摩擦磨损性能及摩擦系数的影响因素进行了研究，指出速度或表面温度、材料的导热和蓄热能力、表面状况或减摩效果、材料的相溶性等会对摩擦材料的摩擦系数产生影响.王勤忠等［18］对货车转向架的相对摩擦因数进行了实验研究，取得了弹簧行程和振动频率与相对摩擦因数之间的关系.

可见关于摩擦系数影响因素的研究虽有涉及，但针对摩擦系数随各种影响因素的实际变化趋势的系统研究并未开展，且目前研究中摩擦实验多采用旋转对磨的方式，而减振器摩擦板实际工作状态为直线往复振动，采用往复振动的实验方式更能反映其真实的摩擦特性.因此，本文设计了在往复振动工况下测量摩擦系数的实验装置，系统研究了压力、频率、幅值对摩擦板摩擦系数的综合影响，用以指导斜楔减振器的设计问题.

1 实验过程

1.1 实验装置设计

实验中所研究摩擦板为某公司提供的用于转K6 转向架斜楔主摩擦面的摩擦板，侧架摩擦板为正方形平板结构，安装于侧架立柱.斜楔摩擦板的圆柱部分可与斜楔表面安装孔配合，由定位孔对其进行定位和固定.

为测量两摩擦板间的摩擦系数，根据其形状尺寸设计了如图1 所示的动态摩擦系数测量装置，斜楔摩擦板与侧架摩擦板安装于图1 中箭头所指处.为清楚表示各零件名称，绘制如图2 所示的测量装置零件示意图.

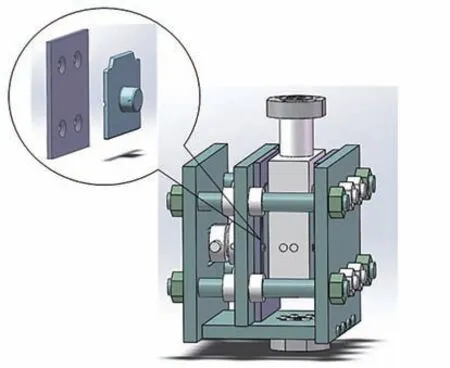
图1 动态摩擦系数测量装置三维模型Fig.1 Three-dimensional model of dynamic friction coefficient measuring device

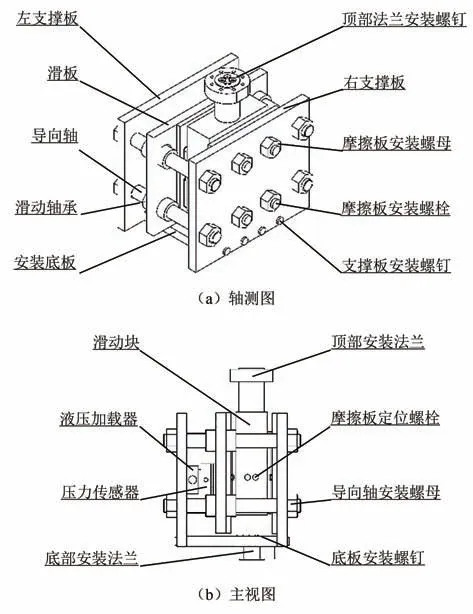
图2 动态摩擦系数测量装置零件示意图Fig.2 Schematic diagram of measuring device part for dynamic friction coefficient

由图1 与图2 可知，装置分为固定和运动部分.固定部分为安装底板、左右支撑板以及滑板和导向轴.两侧架摩擦板用螺栓安装于右支撑板与滑板，滑板可在导向轴上移动以调整侧架摩擦板的位置.该部分整体安装于实验机固定端.运动部分为滑动块，尺寸大于摩擦板，保证贴合并支撑摩擦板，避免加载后摩擦板弯曲，摩擦板圆柱部分与其中间装配孔配合，通过螺栓固定，滑动块整体安装于实验机运动端，振动轴带动滑动块运动，使两摩擦板产生相对运动.

使用液压加载器作为加载方式，放置于滑板与左支撑板之间，挤压滑板对摩擦副施加压力，同时在液压加载器和滑板之间放置压力传感器测量摩擦副压力.

1.2 实验装置校准

由于滑板与导向轴间存在摩擦力，摩擦副所受实际压力小于液压加载器施加压力，滑板倾斜较大甚至会产生摩擦自锁，施加压力完全被摩擦力抵消，因此应尽量减小摩擦力影响.首先，考虑同种金属黏着特性，在滑板与导向轴间安装铜合金滑动轴承，同时可以利用石墨润滑减小摩擦力；其次，液压加载器应位于滑板中心处，且选用较长滑动轴承，避免加载时滑板受力点不在中心发生倾斜造成其配合孔内壁与导向轴发生挤压，产生较大摩擦力.使用液压加载器对该装置加载时，在滑板两侧同时放置压力传感器，两传感器所测压力大小近似相等，说明滑板与导向轴间摩擦力可忽略不计.

实验过程中，若滑动块向一侧偏离，左右摩擦副的压力将不同，故应保证滑动块中轴线与两摩擦副对称线重合.因此安装底板的安装孔采用腰型孔，施加载荷后令滑块上下运动，直至压力传感器测得数据在确定范围内波动，说明此时滑动块中轴线与两摩擦副对称线重合.重复此过程调整载荷至所需压力，再将安装底板的安装螺钉拧紧，此时左右两摩擦副压力近似相等.

1.3 实验设备及采集系统

将动态摩擦系数测量装置安装于Instron 万能实验机，并连接DHDAS 信号采集系统搭建实验系统进行动态摩擦系数测量实验，实验系统如图3 所示，使用Instron 万能实验机提供激振力，使滑动块往复振动.位移传感器位于运动端，采集运动块位移数据；力传感器位于固定端，采集整体实验装置拉压力数据；压力传感器放置于液压加载器与滑板间，连接DHDAS 信号采集系统，同步采集摩擦副所受压力大小.

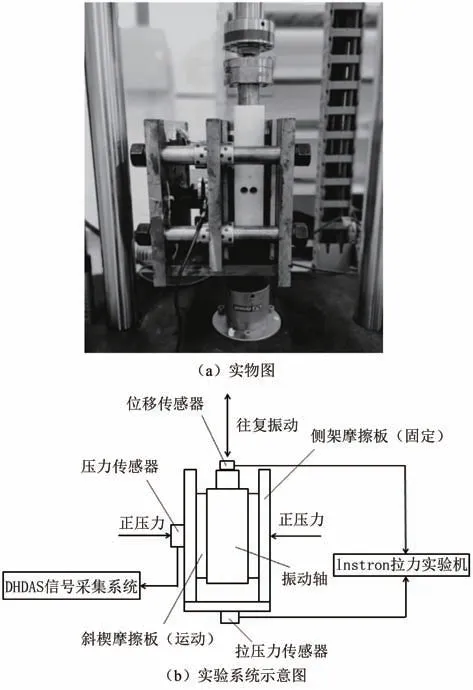
图3 实验系统Fig.3 Experiment system

1.4 实验参数

列车运行状态直接影响摩擦副工况条件：列车载重决定摩擦副压力大小，运行速度决定摩擦副相对运动的频率大小，轨道起伏程度及减振器弹簧刚度决定了振幅大小.因此将振幅、频率和压力作为研究变量，即可反映列车运行状态对摩擦板摩擦系数的影响.

相比于文献［15-17］以相对速度和温度作为摩擦实验的研究变量，本文中的研究变量为频率f、振幅A和压力F，频率和振幅决定了相对速度的大小，同时相对速度和压力也决定了摩擦热引起的温度变化，因此将频率、振幅及压力作为研究变量已经考虑了相对速度和温度对于摩擦系数的影响，不再将其作为实验变量.设置测量频率f为1，2.5，5，…，10 Hz，振幅A为2.5，5，…，15 mm，压力F为1，2，3，4 kN.

1.5 数据处理方式

摩擦副切向力与正压力的比值即为摩擦系数，摩擦副切向力与整体装置所受拉压力平衡，因此可得到摩擦系数计算公式为

式中：μ为摩擦系数；FT为实验机传感器测得装置整体所受拉压力；F为压力传感器所测得摩擦副所受正压力大小.

由于接近位移极限位置处拉力换向对整个机器造成冲击，同时位移范围越大侧压力波动更大，因此较大位移范围内误差更大；其次摩擦板运动过程非匀速，为使计算摩擦系数的动态摩擦过程相对速度近似恒定，因此应使用位移位于一定范围内的数据.取5 s 后10 个周期以上的稳定数据，对位移在振幅大小50%以内的数据所对应的摩擦系数求平均值，作为该工况下的摩擦系数.

2 实验结果分析

2.1 压力对摩擦系数的影响

将摩擦实验所测得的确定f、A工况下的摩擦系数进行比较，得到摩擦系数随压力的变化曲线见图4.

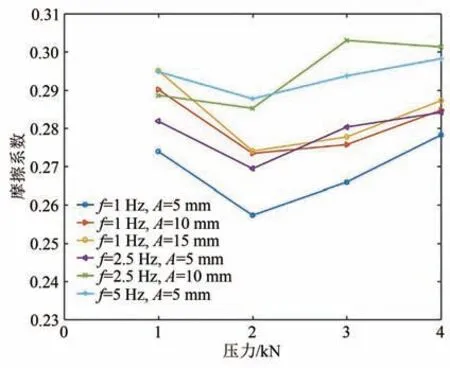
图4 摩擦系数随压力的变化曲线Fig.4 Curves of friction coefficient changing with pressure

由图4 可知，摩擦系数随压力的增大呈现先减小后增大的趋势.在1 kN 到2 kN 的较低压力范围内，摩擦系数呈现随压力增大而减小的趋势，这符合粗糙表面的接触理论［19］所决定的变化规律.

两固体表面接触时，实际接触只发生在表观接触面积的极小部分上，实际接触面积对于摩擦力大小起决定性影响，根据理想粗糙表面接触模型［19］，粗糙表面可视为许多排列整齐，曲率半径、高度相同的粗糙峰组成，各峰承受载荷和变形完全一样且互不影响.对于塑性接触状态，实际接触面积与压力成正比；对于弹性接触状态，实际接触面积与压力的2/3 次方成正比.

由于实际材料表面接触通常是一种混合的弹塑性系统，即较高峰点产生塑性变形，而较低峰点产生弹性变形.随着载荷增加，两表面法向变形量增大，而塑性变形的峰点数亦相应增多.所以接触面积S与压力F之间满足的关系为

式中：2 3 ＜n＜1；k为常数.

而摩擦力Ff与实际接触面积S成正比

式中：k′为常数.

则

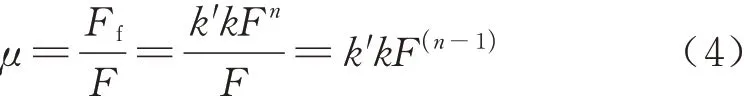
由式（4）可知，由于接触界面处于弹塑性接触状态，实际接触面积与压力间为非线性关系，使得实际接触面积增大比例小于压力增大比例，因此在压力为1 kN 到2 kN 之间时摩擦系数随压力的增大而减小.

随着压力的不断增大，较多只发生弹性变形的接触峰点应力不断达到屈服极限而产生塑性变形.此后接触点应力不再改变，而接触面积继续扩大以承受增加的载荷，整个接触面的峰点几乎均处于塑性接触状态，由于塑性接触状态下实际接触面积的大小与压力成正比，此时压力变化不再因接触状态引起摩擦系数的变化.

由于接触点的应力值为摩擦副中软材料的屈服极限σs，实际接触面积为S，则二者之间满足关系

摩擦过程中接触点处由于较大压力和速度产生一定的摩擦热，接触点软化并在压力作用下紧密贴合，冷却后固结为一体，称为黏着结点.黏着结点处剪切力的大小即表现为摩擦力，在滑动摩擦中，黏着结点吸热软化、散热固结的形成过程和剪切断裂过程交替发生，此现象即黏着效应［20］.

黏着效应产生的摩擦力Ff为

式中：τb为黏着结点的剪切强度.则摩擦系数为

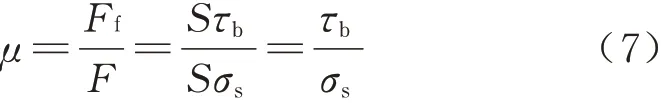
摩擦热功率为

式中：v为摩擦副相对运动速度.

相同频率和振幅时，压力增大使摩擦副接触更加紧密，同时由式（8）可知压力越大产生摩擦热更多，黏着结点的剪切强度增强，因此在压力为2 kN到4 kN 之间时摩擦系数随压力的增大而增大.

综上所述，摩擦系数随压力的增大呈现先减小后增大的趋势.

2.2 振幅对摩擦力的影响

将摩擦实验所测得的确定f、F工况下的摩擦系数进行比较，得到摩擦系数随振幅的变化曲线见图5.

由图5 可知，摩擦系数随振幅增大均呈增大趋势，且在振幅较小时增大趋势更明显，振幅越大，摩擦系数增大越缓慢.

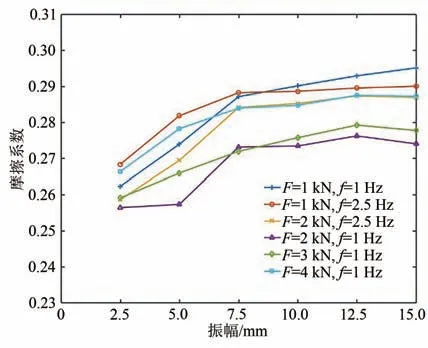
图5 摩擦系数随振幅的变化曲线Fig.5 Curves of friction coefficient changing with amplitude

当滑动速度不引起表面性质变化时，摩擦系数几乎与滑动速度无关.然而滑动速度引起发热和温度变化，改变了表面层的性质以及摩擦过程中表面的相互作用和破坏条件，因而摩擦系数必将随之变化［21］.

在本实验中，由于摩擦过程中摩擦副之间的相对速度由频率和振幅共同决定，频率确定时相对速度会随振幅的增大而增加，由式（8）可知速度升高而产生更多的摩擦热导致黏着程度更大，黏着结点的剪切强度增大而使得摩擦系数增大，因此摩擦系数随振幅的增大呈现增大的趋势.

2.3 频率对摩擦系数的影响

将摩擦实验所测得的确定A、F工况下的摩擦系数进行比较，得到如图6 所示的摩擦系数随频率的变化曲线.

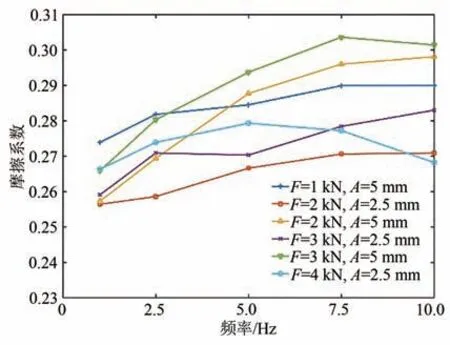
图6 摩擦系数随频率的变化曲线Fig.6 Curves of friction coefficient changing with frequency

由图6 可知，压力较低时摩擦系数随频率增大呈增大趋势；压力为3 kN 的工况下在频率为10 Hz时摩擦系数略微降低，压力为4 kN 工况下在频率7.5 Hz 时便出现摩擦系数下降现象.

在1 Hz 到5 Hz 的频率范围内，加载频率的升高同样引起接触区域温度的升高从而导致黏着结点剪切强度增大，引起摩擦系数的增加，因此在较低频率时呈现摩擦系数随频率变化呈现增大的趋势.频率达到一定程度后，摩擦副接触区域产生摩擦热过大，温度过高使得接触区域的微凸体发生熔融，高分子材料的低导热率使得接触区域产生的摩擦热聚集，熔融结点不能及时冷却黏接，从而出现摩擦系数的降低.

对振幅为5 mm 工况下的摩擦系数进行比较，可得4 种不同压力下摩擦系数随频率的变化曲线对比见图7.

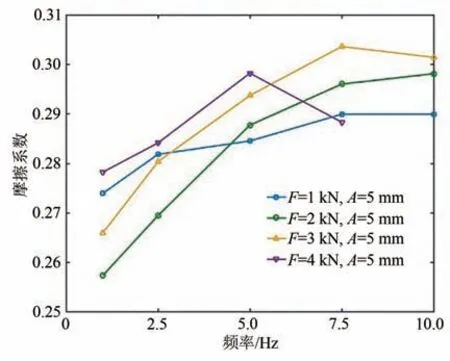
图7 4 种压力下摩擦系数随频率的变化曲线对比Fig.7 Curves comparison of friction coefficient changing with frequency under four different pressures

由图7 可知，在1 kN 和2 kN 时，摩擦系数随频率呈增大趋势，未出现下降.3 kN 时摩擦系数在10 Hz 时出现减小，4 kN 时摩擦系数在7.5 Hz 时出现减小.即压力越大，摩擦系数开始出现下降趋势所对应的频率越小.这是由于摩擦副压力大小也会影响摩擦副接触区域的温度，要达到使微凸体软化的温度，压力越大，所需要的相对速度越小.

对压力为4 kN，振幅为2.5 mm 工况下摩擦系数随频率的变化以及压力为4 kN，频率为1 Hz 工况下摩擦系数随振幅的变化进行比较，可得到高频小振幅与低频大振幅两种工况下摩擦系数变化曲线对比，如图8 所示.

由图8 可知，压力相同时，虽两类工况摩擦副相对速度近似相同，但由于小振幅工况下相对运动范围比大振幅工况的相对运动范围小，即摩擦热产生区域更小，导致其散热速度小于低频率大振幅工况，更容易在黏着结点未冷却黏结时即发生剪切，因此频率的升高比振幅的增大更易导致摩擦系数的降低.

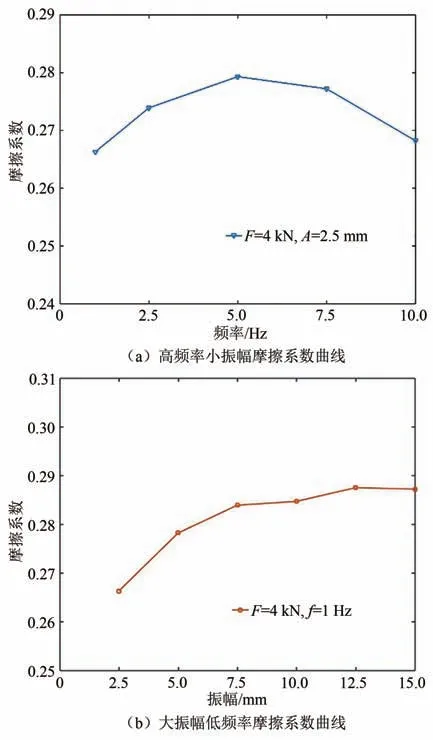
图8 高频率与大振幅摩擦系数变化曲线对比Fig.8 Comparison of friction coefficient curves under high frequency and large amplitude

综上可得，频率和振幅影响摩擦板的相对运动速度的同时也影响了摩擦区域的大小，即同时影响摩擦热功率及其散失速度，而以往研究中将相对速度作为研究变量，忽略了在不同振幅的往复摩擦情况下摩擦热散失速度的差异，因此在往复振动工况下测量其摩擦系数，用频率、振幅代替相对速度作为摩擦特性研究的变量更加符合斜楔减振器实际工况条件.

3 多变量摩擦系数模型

列车在行驶过程中工况复杂，频率、振幅、压力3 个变量会因工况条件同时发生变化，因此有必要研究其对摩擦系数的综合影响.在确定一个变量的工况下拟合得到摩擦系数和另两个变量的函数关系，并比较确定变量大小不同时函数关系的区别，进而分析频率、振幅、压力同时变化对摩擦系数的影响规律.

3.1 摩擦系数单变量拟合形式

对摩擦系数进行单一变量的拟合以确定双变量拟合的函数形式，设摩擦系数μ随单一变量X变化时的函数关系可拟合成多项式形式

式中：X为自变量；r为多项式次数；m为多项式阶数；ar为多项式系数.则双变量拟合的表达式为［22］

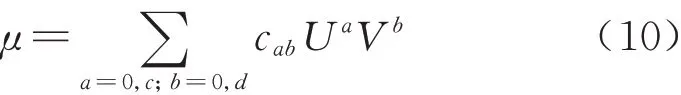
式中：U和V为拟合自变量；a和b为双变量拟合多项式中两个变量的次数；c和d为两个变量的最高次数，等于该变量与摩擦系数的单变量拟合多项式的阶数；cab为多项式系数.

取部分两个变量相同的数据对摩擦系数和另一变量以二次多项式拟合可得

式中：RMSE 为均方根误差；R2为相关系数.

可看出相关系数R2均在0.95 以上，因此以二次多项式进行单一变量拟合所得函数足够逼近真实值，能准确反映其变化规律.

3.2 确定振幅下双变量摩擦模型

摩擦系数μ与频率f、压力F的双变量拟合表达式为

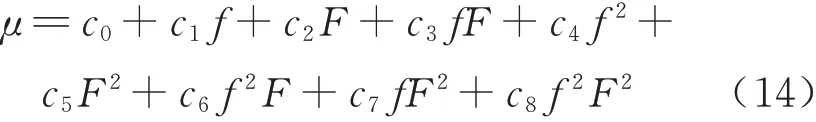
分别对A为2.5 mm、5 mm、7.5 mm 工况下的μ与f、F进行双变量拟合得到各自的双变量拟合表达式，并依此绘制如图9 所示的振幅确定时摩擦系数与频率和压力的拟合曲面.

由图9（a）可知，在小振幅工况条件下，摩擦系数随频率的变化呈增大趋势，且增大速度逐渐减小；随压力的变化呈先减小后增大的趋势，符合摩擦系数由粗糙表面的接触情况和黏着效应同时决定的机理.

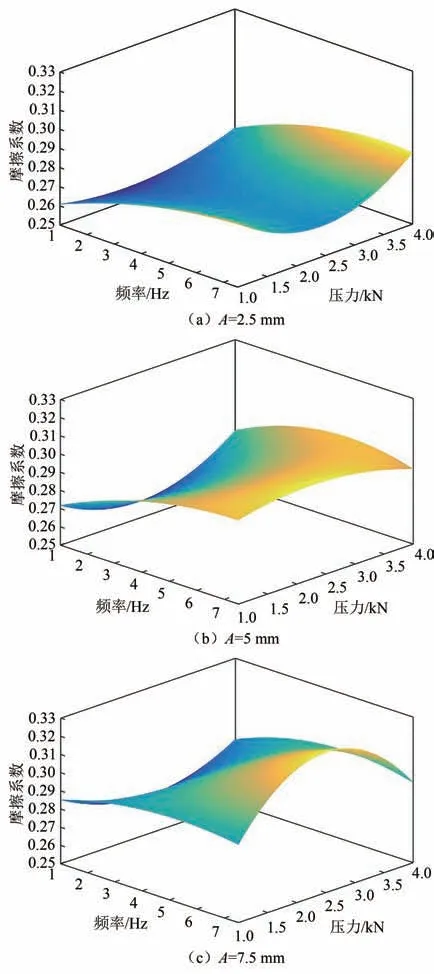
图9 A 确定时μ 与f 和F 的拟合曲面Fig.9 Fitting surface of μ with f and F when A is determined

由图9（b）可知，振幅增大以后，频率和振幅对摩擦系数的影响规律随均出现变化.在压力为4 kN的重载情况下，摩擦系数随频率的增大出现减小趋势；在频率为7.5 Hz 的高频情况下，摩擦系数随压力的变化从1 kN 开始便呈现增大趋势，增大速度逐渐减小，随后有略微的减小趋势.在较大振幅、重载情况下，频率在升高过程中的黏着效应相较于图9（a）的小振幅情况更强，在频率升高到6 Hz 左右，摩擦热的聚集使接触表面的微凸体出现软化甚至熔融状态，因此摩擦系数系数开始略微减小.对于随压力的变化，由于图9（b）振幅相较于图9（a）振幅增加，导致在较低压力时黏着效应即对摩擦系数的影响起主要作用，因此摩擦系数随压力变化也持续增大.

由图9（c）可知，大振幅高频率情况下，摩擦板相对运动速度很快，低载情况同样会产生大量摩擦热，导致摩擦系数减小. 对比图9（a）、图9（b）、图9（c）振幅持续增大的过程，压力变化对摩擦系数的影响规律由图9（a）中先由粗糙表面的接触状态起主导作用后再由黏着效应起主导作用，转变为图9（b）中黏着效应始终起主导作用，再转变为图9（c）中在重载时出现摩擦热导致的摩擦系数减小.

3.3 确定频率下双变量摩擦模型

摩擦系数μ与振幅A、压力F的双变量拟合表达式为

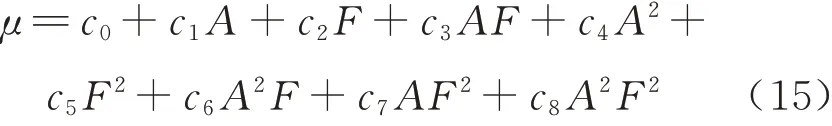
分别对f为1 Hz、2.5 Hz、5 Hz 工况下的μ与A、F进行双变量拟合得到各自的双变量拟合表达式，并依此绘制如图10 所示的频率确定时摩擦系数与振幅和压力的拟合曲面.

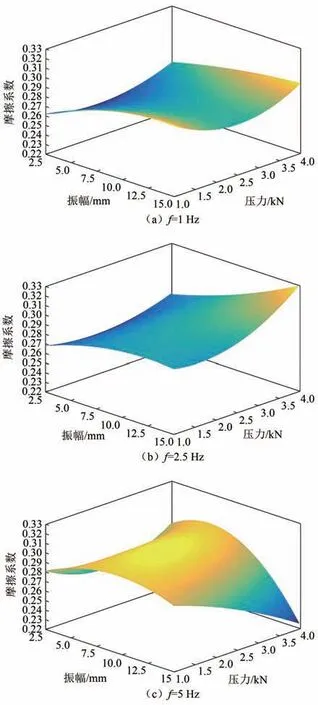
图10 f 确定时μ 与A 和F 的拟合曲面Fig.10 Fitting surface of μ with A and F when f is determined

由图10（a）可知，在低频情况下，摩擦系数随振幅增大呈持续增大趋势，随压力增大呈先减小后增大的趋势，与图9（b）的变化规律相同.

由图10（b）可知，在频率为2.5 Hz 情况下，重载时摩擦系数随振幅的变化仍未出现下降趋势，这与图9（b）中重载时摩擦系数随频率增大出现减小趋势不同.两种情况下摩擦板相对速度近似相等，然而小振幅工况下相对运动范围比大振幅工况小，导致其散热速度小于大振幅工况.振幅增大时，摩擦热增加的同时散热也会加快，一定程度上削弱了摩擦热的累积，因此相比频率，振幅增加引起的温度增加会更小.

由图10（c）可知，频率增大到5 Hz 后，摩擦系数下降趋势非常明显.在15 mm 大振幅工况下，摩擦系数随压力变化呈持续下降趋势.图9（c）中振幅为7.5 mm，最大频率为7.5 Hz，图10（c）频率为5 Hz，最大振幅为15 mm，二者相比，图10（c）中摩擦板的相对速度大于图9（c），在相同压力情况下，频率5 Hz、振幅15 mm 的工况产生的摩擦热更多，摩擦热聚集引起的摩擦板接触表面微凸体熔融更严重，因此摩擦系数随压力变化始终呈现减小趋势.

3.4 确定压力下双变量摩擦模型

摩擦系数μ与频率f、振幅A的双变量拟合表达式为

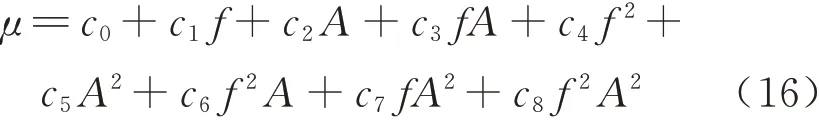
分别对F为2 kN、4 kN 工况下的μ与f、A进行双变量拟合得到各自的双变量拟合表达式，并依此绘制如图11 所示的压力确定时摩擦系数与频率和振幅的拟合曲面.

由图11（a）可知，摩擦系数随频率和振幅的变化规律类似，均为持续增大.由图11（b）可知，在压力为4 kN 的重载情况下，摩擦系数在频率和振幅均最大时出现大幅下降的情况，此时频率、振幅、压力三者乘积相较于图9、图10 及图11（a）中各工况为最大，摩擦热引起的摩擦板熔融现象最为剧烈，因此导致摩擦系数大幅下降.

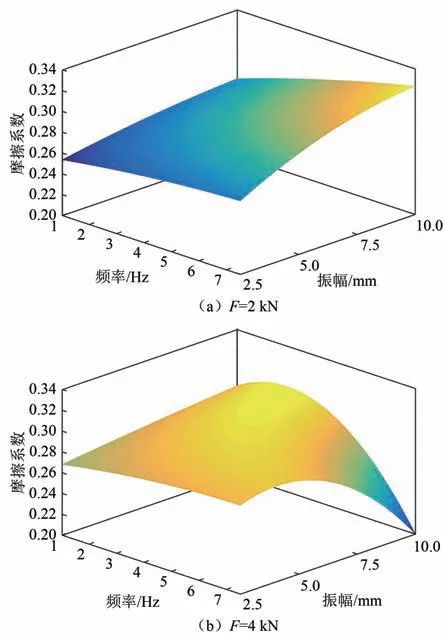
图11 F 确定时μ 与f 和A 的拟合曲面Fig.11 Fitting surface of μ with f and A when F is determined

基于拟合出的函数关系可看出，实验数据具备很强的规律性，可通过此函数关系改进斜楔减振器参数以获得合适的摩擦系数.

针对于重载列车，高速行驶时摩擦板所受压力和振动频率都很大，斜楔摩擦板的摩擦系数增大，列车运行中轨道对转向架的瞬时刚性冲击会直接传给车体，针对此问题，可增大减振器弹簧的刚度，将摩擦板的振动范围控制在较低振幅以内，以此减小摩擦系数.若列车运行轨道起伏较大时，高速重载列车摩擦板所受压力以及振动的频率和振幅均处于较高水平，摩擦板的摩擦系数会大幅下降，使列车受迫振动，振幅无法有效衰减，列车随轨道不平持续颠簸，针对此情形，也应注意增大减振器弹簧刚度，减小摩擦板往复振动的振幅，防止因摩擦板过热导致摩擦系数大幅下降.

对于载重量较小的列车，由于摩擦板所受压力较小，摩擦系数相对较小的情况下易出现列车持续颠簸的问题，可通过减小减振器弹簧刚度的方式增大摩擦系数，使受迫振动振幅能有效衰减.