改进PSO 的协调控制系统的模糊模型
2022-07-14庄恒悦马永光常志伟吴盛平
庄恒悦,马永光,常志伟,吴盛平,赵 魏
(华北电力大学控制与计算机工程学院,河北 保定 071003)
火电机组是中国电网的主力机组,协调控制系统是超临界机组的控制核心,其控制结果将直接影响整个机组的性能[1]。由于超临界机组具有惯性、迟延等非线性的特点,而现行的先进控制策略大多借助结构简单且精度高的数学模型,因此对协调控制系统的建模是开展提高机组效率、优化控制等研究的基础[2]。
对超临界机组的建模大多采用机理建模和非机理建模。机理建模[3]是利用以能量和动量为主的守恒关系建立动态模型,建模工作难度较大。而依靠输入输出数据的进行系统辨识的非机理建模[4]易于获取,可靠性高。通过采用T-S 模糊辨识的智能建模方法,建立IF-THEN 语句描述系统输入输出之间的非线性关系。使用模糊C-均值聚类算法辨识系统的前件结构,后件的辨识则使用递推最小二乘法,在采用一种迭代次数少的粒子群算法对参数寻优。通过Matlab 仿真,结果表明该算法在协调控制系统模型上有较好的应用效果。
1 模型建立
单元机组协调控制系统(CCS)的主要任务是克服锅炉慢特性和汽轮机快特性间不平衡的影响[5]。各输入输出变量对系统的影响程度不等,CCS 的3 个重要输入变量为燃料量B、给水流量W和汽轮机阀门开度μ。多输入变量间的耦合性和非线性均对系统输出功率作用,这也是影响建立CCS 模型精度的关键因素。
1985 年TAKAGI 和SUGENO 提出了以模糊集合理论为基础的T-S 模糊模型[6]。本质上是模糊逻辑的非线性系统建模方法,而每条规则的后件辨识又是线性系统,通过隶属度函数的连接,将非线性系统以数条模糊规则的形式表达,这使得模型具有半线性化的特征和任意逼近的能力。通常,一个T-S 模糊模型由几个形如IF-THEN 规则的模糊语句组成,为:
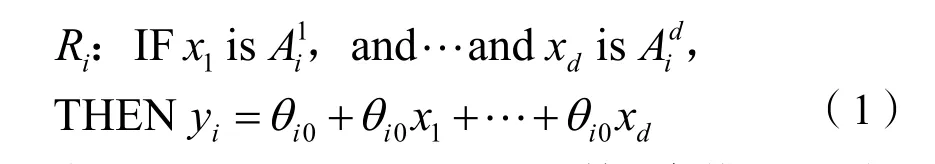
式(1)中:Ri(i=1,2,…,c)为第i条模糊规则,c为模糊规则的个数;X=[x1,x2,…,xd]为系统的输入变量;A为以隶属度函数(MF)为特征的语言项;d为维度;yi是第i条规则的输出;θ为待辨识的后件参数。
T-S 模糊模型建立流程如下。
第一,采用高斯型隶属度函数将输入数据归一化并划分初始样本区间:
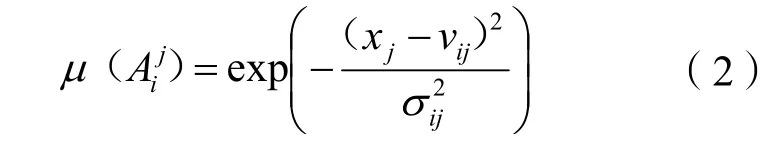
式(2)中:vij和σij分别为第i条规则中第j个位置函数的中心和宽度。
第二,归一化的数据使用模糊C-均值聚类算法(FCM)根据目标函数搜索最优目标加权点,目标函数为:

这里的约束条件有:对于任意i,j有所属隶属度介于[0,1];对任意j有所有隶属度相加等于1,其中迭代结束条件是
第三,反复调整模糊隶属度矩阵U=[μij]∈R,i=1,2,…,c,j=1,2,…,d和聚类中心矩阵,得到最小的迭代次数,选取最优的聚类中心,聚类中心矩阵为:
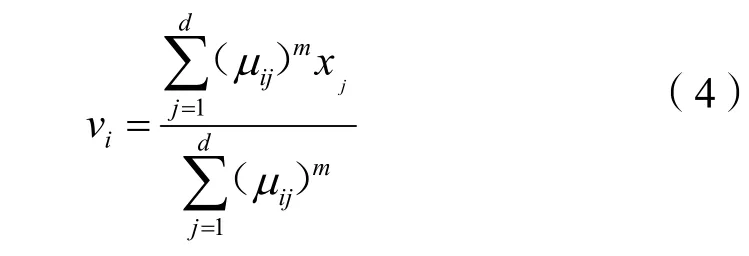
式(4)中:m为加权指数,一般取值2。
第四,递推最小二乘法(RLS)既可避免高阶矩阵求逆运算,又能提高参数识别的准确性。估计参数值的迭代公式为:

这里设定初始值(0)=0,P0=αI(α是个很大的数,取105;I为单位矩阵)。
第五,T-S 模糊模型的最输出可以通过加权平均的去模糊化来计算,方法为:

式(6)中:权重为输入的第i条规则中的加权函数;Π为模糊算子。
第六,给定优化性能指标函数——最小均方误差MSE,为:

式(7)中:yj为实际输出;为模型输出。
2 改进粒子群算法
粒子群算法[7(]Particle Swarm Optimization,PSO)最早源于对鸟群觅食行为的研究。一群鸟在随机搜寻食物,食物位置未知,但是当前的位置与食物的距离已知。简单有效的策略是寻找鸟群中离食物最近的个体来进行搜索。PSO 算法就从这种生物种群行为特性中得到启发并用于求解优化问题。在函数优化、图像处理等多领域都得到了广泛的应用。但是PSO 算法存在早熟收敛、易于陷入局部极值等问题,文献[8]调整了PSO 的参数,引入了惯性权重来平衡算法的全局探测和局部开采能力。
虽然粒子群在求解优化函数时,表现了较好的寻优能力;通过迭代寻优计算,能够迅速找到近似解,但基本的PSO 容易陷入局部最优,导致结果误差较大。基本PSO 的改进有2 个方向:①将各种先进理论(如混沌技术、神经网络技术、自适应技术)引入到PSO算法,研究各种改进PSO 算法;②将PSO 算法和其他智能优化算法相结合,研究各种混合优化算法,达到取长补短、改善算法某方面性能的效果。
这里用到的模型建立及算法流程如图1 所示。

图1 模型建立及参数优化流程图
3 仿真分析
3.1 测试函数
以y=x(1)2+x(2)2-x(1)×x(2)-10×x(1)-4×x(2)+60 为测试函数,分别测试不同粒子群优化算法的迭代过程,从图2 可以看出以自适应调整权重的迭代次数最少,因此采用权重随着粒子适应度值的改变而改变的粒子群优化算法,权重规则为:
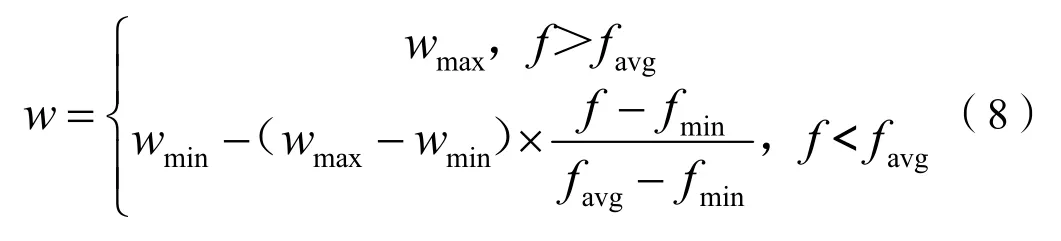

图2 不同粒子群优化算法的迭代过程比较
3.2 算法在单输入单输出(SISO)系统的测试
Box-Jenkins 数据[9]是系统辨识中经常被使用的例子,这是一个SISO 动态系统,输入u(t)是进入煤气炉的煤气流量,输出y(t)是排烟中CO2浓度,一共有296 对数据组。为对比其他文献结果,选用{u(t-1),u(t-2),u(t-3),y(t-1),y(t-2),y(t-3)}作为输入变量组合。采用本文的方法辨识的结果如图3所示。从测试结果上可以看出,误差抖动较小,本文的方法在煤气炉数据辨识上有较好的效果,适用于SISO 系统中。
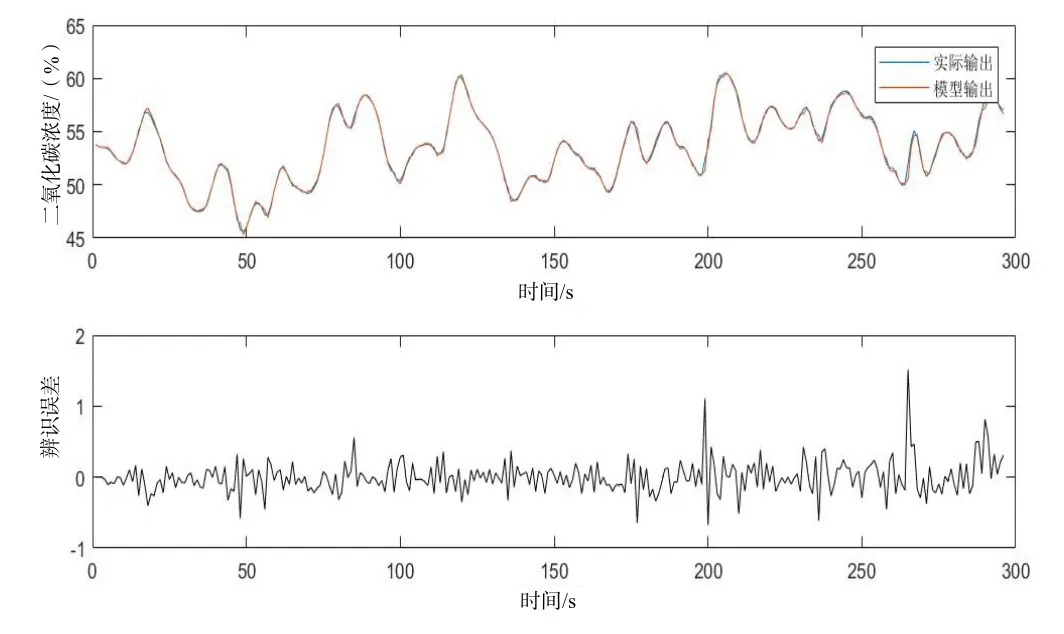
图3 模糊模型在煤气炉模型的测试结果
3.3 协调控制系统的应用
采集机组的现场运行数据,负荷变化范围为497~620 MW,选取2 000 组数据,并拆分成1 500 组训练和500 组预测。通过T-S 模糊建模的快速性和有效性以及辨识所得模型的准确性,选取主要影响变量,忽略次要影响变量。对于三输入单输出的机组协调控制系统模型,其选取的数学模型和实验参数如表1 所示。基于现场输入输出数据和模糊模型结构,模型前件结构辨识和后件参数辨识要反复交替实验,直到获取满意效果。
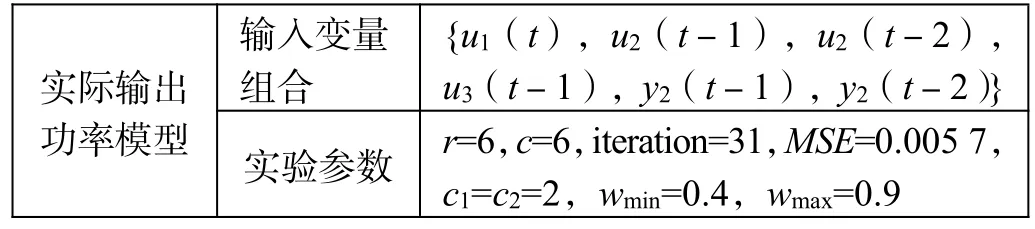
表1 不同变量输入组合及结果参数
其中,学习因子c1、c2具有自我总结和向优秀个体学习的能力,从而使微粒向群体内或领域内的最优点靠近。c1、c2分别调节微粒向个体最优或者群体最优方向飞行的最大步长,决定微粒个体经验和群体经验对微粒自身运行轨迹的影响。学习因子较小时,可能使微粒在远离目标区域内徘徊;学习因子较大时,可使微粒迅速向目标区域移动,甚至超过目标区域。
惯性权值w∶w越大,微粒飞行速度越大,微粒将会以更长的步长进行全局搜索;w较小,则微粒步长小,趋向于精细的局部搜索。因此,设定w的取值区间,在搜索初期设w为一个较大值,然后随着迭代次数的不断增加,逐渐降低w的值;从而达到全局最优。
IPSO 对输出功率的辨识训练和预测如图4 所示。图4(a)是改进PSO 在实际输出功率上的辨识训练结果,曲线吻合良好,模型输出曲线对系统实际曲线有较高的的跟踪度,图4(b)是对输出功率的预测模型,辨识误差稳定在0.5 左右,曲线趋势一致,说明所用算法运用效果良好。
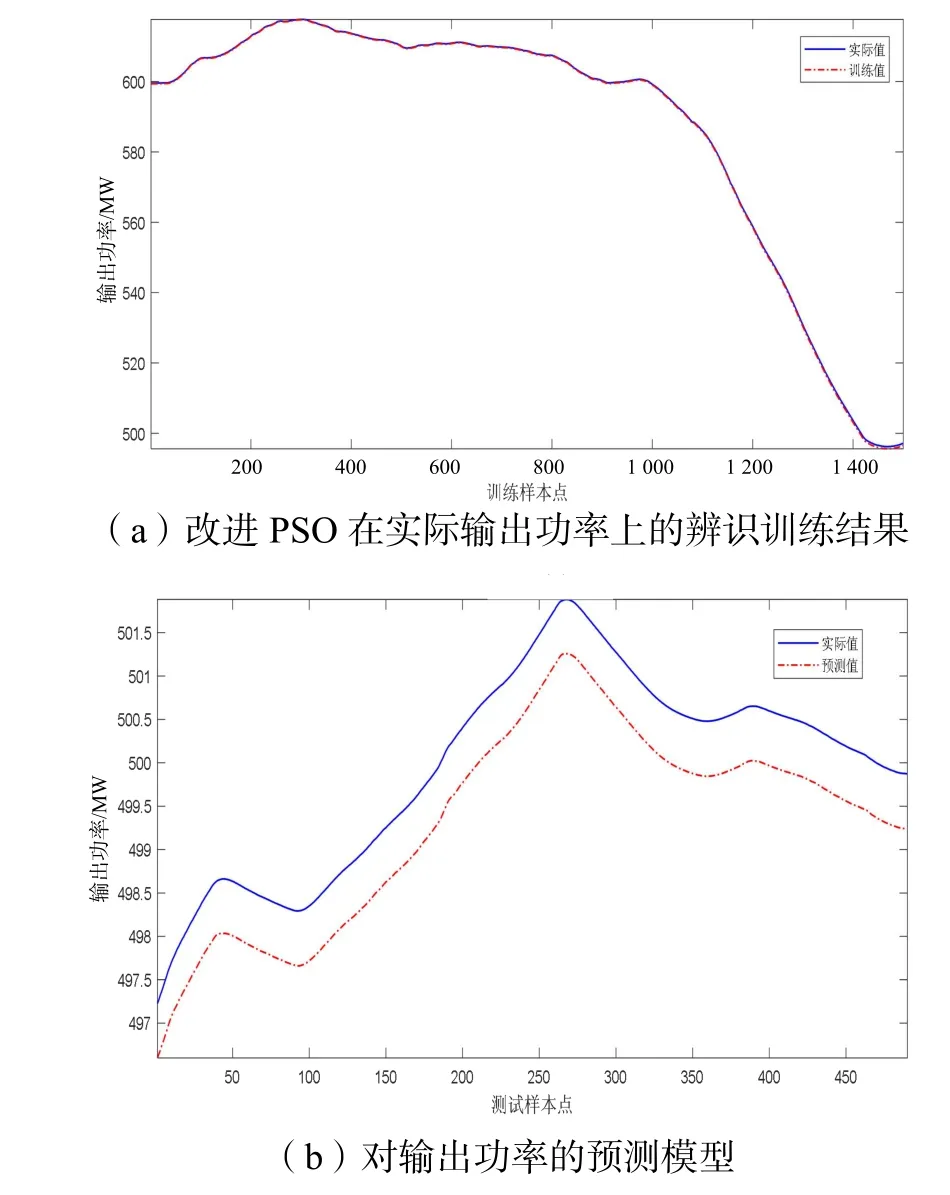
图4 IPSO 对输出功率的辨识训练和预测
4 结论
本文以协调控制系统为研究对象,构建T-S 模糊模型,结合改进的PSO 算法对模型后件参数寻优辨识。仿真结果表明,构建出的机组协调控制系统模型,既避免了求解目标函数时容易陷入极值问题,又表现出聚类速度快且效果明显、数据拟合误差小、精度高的优点,为实际工业生产过程中机组协调控制系统提供了可靠基础。
