基于MATLAB 的汽车直线加速工况下振动模型分析

王师夷

（武汉理工大学国际教育学院，湖北 武汉 430070）

1 背景

车辆行驶过程中的行驶品质很大程度上由汽车悬架决定，路面对汽车的激励给予汽车不同频率的振动，这些不同频率的振动也会让人产生不同程度的不适感。汽车悬架是一种负责承受汽车质量并且缓冲路面通过汽车接触地面的部分传递给车身冲击与振动的装置[1]。这就要求车辆的悬架系统能够具有足够的操作稳定性和缓冲性能，以使车辆的悬架系统承受制动力、驱动力和离心力时具有足够的操纵稳定性，避免汽车行驶时产生过大的侧倾与仰倾，并且避免汽车制动时出现明显的点头现象等。尤其是处于高速状态下的汽车对于操纵稳定性会有较严苛的要求，在设计悬架系统时选择的刚度与阻尼参数很大程度上决定了悬架特性。根据以往的研究发现：一台汽车如果想要提升乘客的乘坐体验，需要将悬架变得柔软一些；而为了使车辆更加便于操纵，则需要考虑提升弹簧的韧性；并且在悬架共振频率的范围内，阻尼力起到决定性作用[1]，所以汽车悬架设计需要综合考虑悬架特性中刚度和阻尼因素的影响，并且根据设计和使用要求设定最合适的阻尼和刚度系数[2]。

在汽车行驶时，路面的高低不平整就会作为一种激励使悬架系统与轮胎对其进行响应，不同的反馈就表明了汽车悬架相关参数的区别。但在实际情况中，受诸如路面情况、汽车速度和汽车悬架使用情况等复杂因素的影响，很难准确地找到每一种因素单独对悬架系统性能表现的影响，只有在建立了适当简化的力学模型中才能比较直观和方便地得到确定的影响情况。这对于理解汽车悬架系统对应参数的工作特性，对提高车辆行驶平顺性、稳定性的要求提供了解决的思路与方向。

本文根据牛顿第二定律建立有关参数的方程组，并据此设计完成了半车的四自由度振动模型，同时使汽车受到一个突然的地面起伏激励以模拟汽车在行驶过程中会遇见的一种普遍场景，为汽车悬架系统的阻尼和刚度等参数设计提供一些参考。

2 建立数学模型

2.1 模型建立的假设条件

由于车辆实际行驶过程中悬架系统的响应是由多个因素决定的，并且整车的悬架系统最高拥有8 个自由度。为了方便建立模型，做出如下假设来简化模型：汽车左右两侧的行驶情形一致，汽车整车质量分布均匀，忽略汽车车轮因加减速等原因相对于车身的前后位移。以这几条假设为前提，就可将汽车的整车运动模型进行简化[3]，得出更加容易理解分析的情况和结果。其中所需物理量的数值如表1 所示。

表1 所需物理量的数值

2.2 汽车悬架模型建立

首先按照上文提出的简化假设，选取车身的一侧作为分析的对象，建立汽车的半车身简易模型，如图1所示，这个模型包含独立前后垂直悬架，同时也包含了车身俯仰和弹跳的自由度。

图1 半车身悬架模型

根据牛顿第二定律得出以下方程：

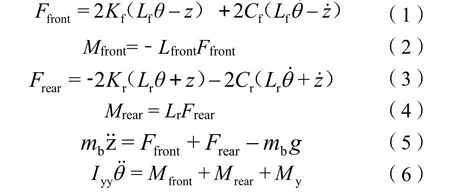
式（1）—式（6）中：Ffront为车辆前悬架向上的力；Kf为前悬架弹性模量；Lf为重心到前悬架的水平距离；θ为俯仰角；z为弹跳距离；Cf为前悬架的阻尼比；θ˙为俯仰角变化率；z˙为弹跳距离变化率；Frear为车辆后悬架向上的力；Kr为后悬架弹性模量；Lr为重心到后悬架的水平距离；Cr为后悬架的阻尼比；Iyy为车身关于重心的转动惯量。

依据上述有关方程，便可以在Simulink 模块中搭建一个半车四自由度悬架模型，如图2 所示。

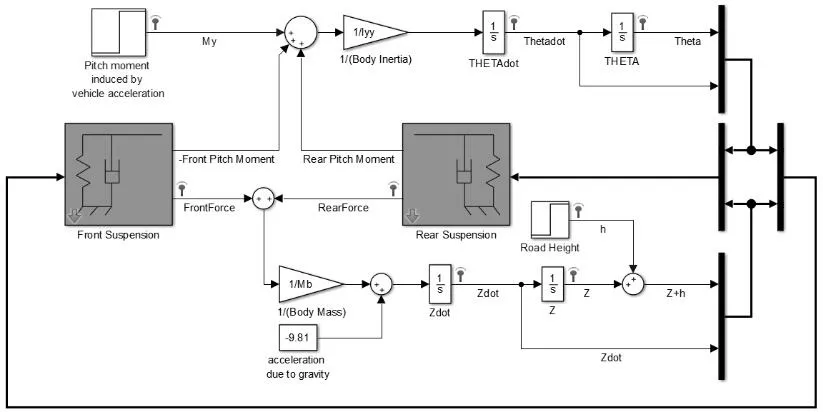
图2 半车四自由度悬架模型

整个模型区分前后轮，每个车轮的悬架系统也可以在Simulink 模块中搭建模型，对前后悬架建模的弹簧和阻尼子系统如图3 所示。将其整合在总体模型中就可以得到完整的模型。

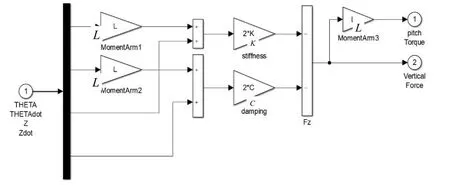
图3 弹簧和阻尼子系统

使用Simulink 可以用较为简单可操作的方式将本悬架模型转变为精细的仿真，同时还能够非常快速地将仿真结果以清晰的图表显示出来，除此以外还提供了交互式图形化环境和可定制模块库来对其进行设计、仿真、执行和测试[4]。这些都会让仿真过程变得更加方便调整，可视化显示结果也能直观地显示出变化，能够较好地满足需求。

2.3 路面情况

本模型选择了大多数汽车都会普遍遇到的悬架振动情形，即汽车加速驶过路面凸起区域。对于同一辆汽车，模拟的悬架变化量就取决于2 个因素，即汽车的加速度所引起的俯仰力矩和凸起的路面高度[5]。本文通过固定车辆经过凸起路面的高度从而改变车辆加速度引起的俯仰力矩，来模拟车辆以不同加速度驶过路面凸起路段所引起的车辆悬架系统振动变化，路面统一设定为一个固定的突变值。

3 仿真分析

首先将表1 的数值输入本半车悬架模型中，输入形式如下。

3.1 较低俯仰力矩仿真

将路面的凸起高度设置为10 mm，车辆加速度引起的俯仰力矩设置为50 N·m。运行仿真模型后得出的结果如图4 所示。

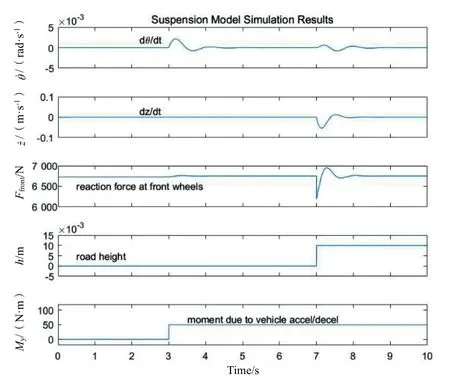
图4 较低俯仰力矩仿真结果

由图4 可知，汽车在第3 s 加速时汽车前轮俯仰角变化率增大，在第7 s 经过地面凸起处汽车前轮先是受力小于稳定值，之后升高达到最大值。

3.2 较高俯仰力矩仿真

同样将路面的凸起高度设置为10 mm，车辆加速度引起的俯仰力矩设置为100 N·m。运行仿真模型后得出的结果如图5 所示。

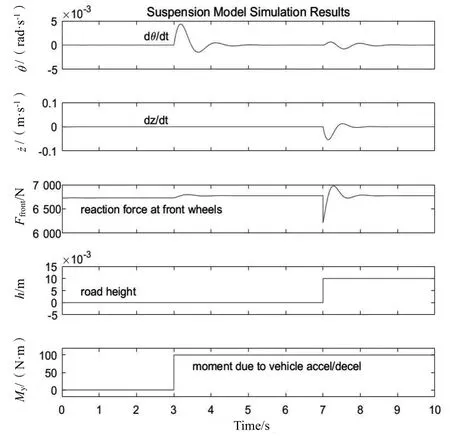
图5 较高俯仰力矩仿真结果

由图5 可知，与较低俯仰力矩时相似，在第3 s汽车开始加速时汽车前轮俯仰角变化率增大，在经过地面凸起时前轮受力突然增大与减小表明车辆的悬架先下沉后上升的运动过程。

3.3 分析比较结果

在其余条件相同，只改变车辆加速度所引起的俯仰力矩的情况下意味着只是改变了汽车的加速情况。对应到现实情况就是汽车以不同的气门开度经过一段硬路面坎后的悬架系统垂直方向的运动。这样的情形在生活中非常常见，例如驾驶汽车路过减速带、行驶时遇到路边坎等，根据人们的日常经验可以得出一个模糊的感性认识：汽车经过类似的小路坎时先向下沉再向上升，如同坐在一个弹簧上。这样的认知显然是不能准确理解悬架系统的工作状况，必须要经过仿真和调整比较参数才能精准地掌握每个因素所带来的影响，才能在实际生产生活中有目的性地调节悬架系统，使之适应不同的设计要求，并且是定量地进行计算分析和改进，这样才能集中资源达到更加良好的表现，有针对性地修改参数以改变车辆的悬架性能。

比较图4 与图5 可知，区别之处主要在2 处突变位置，即突然加速处和经过路面不平处。其中，2 次仿真只是改变了车辆加速度所引起的俯仰力矩，这也就代表2 次仿真改变的只是车辆的加速度大小，这个改变同时还会影响后续经过路面凸起处的振动幅度。第一个区别就是在第3 s 车辆开始加速时由于车辆加速度不同，此时汽车前轮俯仰角变化率的大小随加速度的增大而变大，振荡幅值也是随加速度的增大而数值更大；前轮受到的作用力也有着同样的趋势，也是加速度高的受力更大。另一个区别就是在第7 s 的时候，这时候是汽车前轮正好接触到路面凸起处。分析结果图可知，此时前轮悬架系统先是受力减小再是受力增大至峰值最后趋于平稳。由于车辆加速度引起的车辆行驶速度不同，当汽车加速度值越大或速度值越大时前轮受到的作用力越大，俯仰力矩和垂直方向的速度也变得更大，但是与第3 s 时的差异进行比较发现，没有显著改变。

综上，在只改变车辆加速度和路面凸起高度这2个条件下，在平地行驶时车辆不同的加速度对于车身的俯仰角变化率改变起到主导作用，加速度越大汽车的前后俯仰幅度越明显，但是到达峰值的时间没有较大程度的变化；在车辆经过路面凸起路段，车辆所经过的路面高度对车辆前轮的垂直方向位移和前轮受力数值的改变起到主导作用，加速度的区别对于这种情况影响较小。

4 结果讨论

由分析结果可知，汽车行驶在平整路面上时车辆的加速度大小对于悬架系统的影响是占据主导地位的，为了减小悬架系统垂直方向的位移，此时应该通过减小加速度的方式来获得更加舒适的驾驶体验。当汽车要驶过凹凸不平的路段时，汽车的加速度就显得不再那么重要了，地面凸起或凹陷的高度变成了车辆悬架系统垂直方向位移的主要因素，那么要想减小行驶过程中的不适感就需要驾驶员尽量避开路面不平整的路段，同时也说明了汽车驶过不平整路面时是不太需要注意加速度数值大小的。

5 结论

本文建立了车辆的半车四自由度模型，使用MATLAB 和其中的Simulink 模块，通过修改车辆加速度所引起的俯仰力矩来对车辆加速度以及地面凸起的高度进行了仿真分析，得到了车辆在通过平整路面与不平整路面时车辆前轮的受力情况以及垂直方向的位移数值，为车辆悬架系统设计人员在调整悬架系统参数方面提供了参考。文中建立的半车四自由度仿真模型只考虑到车轮的前后方向与车辆的垂直方向，并没有考虑到汽车行驶过程中同样具有较高频次出现的车辆侧倾现象，因此也就不能完全准确地反映车辆的操纵性能，这就有待进一步分析与优化。本文最终得出的结果与人们普遍认知相符，进一步证明了模型正确，改变模型中的部分参数依然是能够反映车辆行驶过程中的悬架系统特性的。本文设计的模型对实际生产生活中的悬架系统设计也具有一定的实际价值。