高考多选题的命制类型与破解策略

⦿江苏省木渎高级中学 倪 馨

1 引言

2020年新高考山东卷、海南卷数学试题出现了创新性的试题类型——多选题，是一种正确选项数目多于1个且少于等于4个的选择题题型.选出1个或几个正确答案而没有选出全部正确答案的得3分，选错1个得0分，全部选对得5分.充分体现了“破定式，考真功，分层次”的命题理念，更能全面考查学生的数学知识、数学能力和数学核心素养，有利于区分与选拔合格的考生，有效把握数学本质，启发思考，改进数学教学.

2 基于问题多解的判定

例1(2021届江苏省姜堰中学、如东中学、沭阳中学高三上期中数学联考试卷·12)已知函数f(x)=x2-4x+(m2-m)(ex-2+e2-x)(e为自然对数的底数)有唯一零点，则实数m的值可以为( ).

A.1 B.-1 C.2 D.-2

分析：结合函数解析式的变形与转化，引入参数并构造新函数，利用函数奇偶性及函数图象的对称性，结合函数有唯一零点的条件来确定相应的函数零点值，从而建立对应的方程，直接求解相应的参数值.

解析：由于函数f(x)=x2-4x+(m2-m)(ex-2+e-x+2)=(x-2)2-4+(m2-m)(ex-2+e-x+2)，令t=x-2，则g(t)=t2-4+(m2-m)(et+e-t)，其函数的定义域为R.又g(-t)=(-t)2-4+(m2-m)·(e-t+et)=g(t)，故函数g(t)为偶函数，所以函数f(x)的图象关于直线x=2对称，那么要使得函数f(x)有唯一零点，则必须满足f(2)=0，于是4-8+2(m2-m)=0，解得m=-1或2.

故选：BC.

3 基于命题真假的判定

例2如图1，已知正方体ABCD-A1B1C1D1的棱长为1，P是空间中任意一点，下列说法正确的是( ).

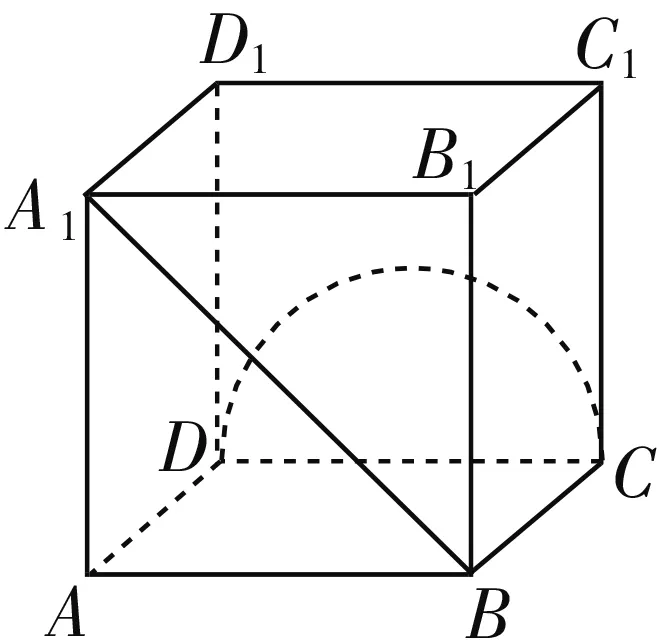
图1

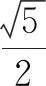
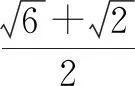
C.若点P在半圆弧CD上运动，当三棱锥P-ABC的体积最大时，三棱锥P-ABC的外接球的表面积为2π

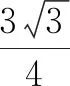
分析：选项A中，结合异面直线所成的角的确定与求解来判断；选项B中，通过三角形与四边形的展开，把立体几何问题转化为平面几何问题来确定动线段之和的最小值问题；选项C中，利用同底的三棱锥中高最大时相应的体积最大来确定点P的位置，进而确定三棱锥的外接球的半径，得以求解球的表面积；选项D中，结合平面α与正方体每条棱所成的角都相等，转化为过同一顶点的三条棱所成的角都相等，数形直观来确定截面的最大位置并确定图形特征，得以确定相应的面积.

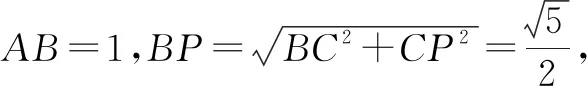
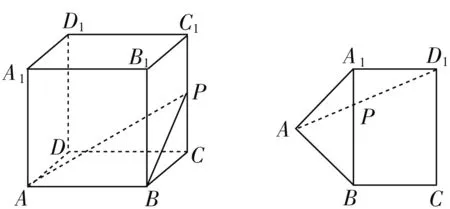
图2 图3

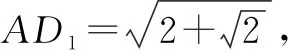
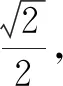
图4 图5

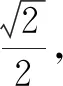
故选：ACD.

4 基于创新背景的判定

例3(2021届福建省厦门重点中学高三上学期12月适应性考试数学试题·12)意大利数学家列昂纳多·斐波那契是第一个研究了印度和阿拉伯数学理论的欧洲人，斐波那契数列被誉为最美的数列，斐波那契数列{an}满足：a1=1，a2=1，an=an-1+an-2(n≥3，n∈N*).若将数列的每一项按照图6所示的方法放进格子里，每一小格子的边长为1，记前n项所占的格子的面积之和为Sn，每段螺旋线与其所在的正方形所围成的扇形面积为cn，则下列结论正确的是( ).

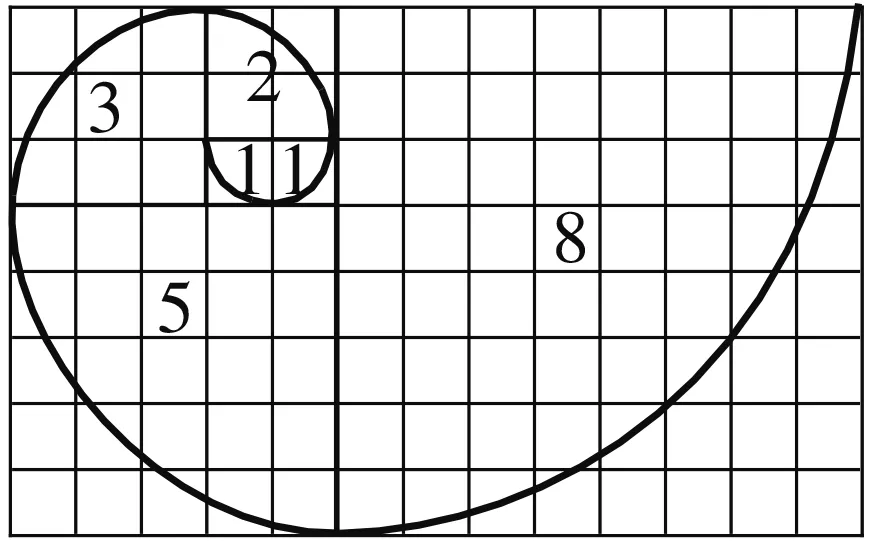
图6

A.a2020是偶数

B.a1+a2+a3+……+an=an+2-1

D.4(cn-cn-1)=πan-2·an+1

分析：结合数学文化背景利用已知条件，根据斐波那契数列的递推规律，利用数论中数列各项的奇偶变化规律、数学归纳法、递推数列的特征方程的建立与求解，以及扇形面积的转化与关系式的确定等，来分别判断各选项的真假情况.

解析：a1=1，a2=1，an=an-1+an-2(n≥3，n∈N*).

对于选项A，结合斐波那契数列及数论规律可知，a3k+1，a3k+2均为奇数，a3k为偶数，而a2020=a3×673+1，则知a2020是奇数，故选项A错误；

对于选项B，当n=1时，a1=a3-1成立；

假设n=k(k∈N*)时，a1+a2+a3+……+ak=ak+2-1成立，那么当n=k+1时，等式左边=a1+a2+a3+……+ak+ak+1=ak+2-1+ak+1=ak+3-1，即当n=k+1时等式也成立，故选项B正确；

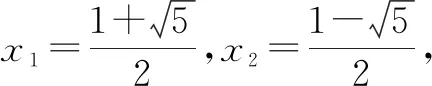
故选：BCD.

5 结论

高考多选题的引入与设置，给数学试卷带来了创新的亮点，在考查学生基础知识和基本能力这一主线上，注重基础性、综合性和应用性的同时，突出了数学核心概念，强化了基础知识和基本技能的有效落实，强调以核心素养为导向，给不同层次的学生增加了得分机会，也更精准地测试和区分不同层次学生的数学基础和数学能力水平.