知识巧交汇 数列妙应用
2022-07-13安徽省阜阳市红旗中学王茂快
⦿安徽省阜阳市红旗中学 王茂快
1 引言
在“知识网络交汇点处设计试题”是高考数学大纲的明确要求与高考数学命题的指导思想之一,作为高中数学的主干知识之一的数列,更是多知识交汇与综合的重要场所,是创新应用与创新意识的更深层次体现,在高考中的地位将越来越重要,是每年高考数学中的热点与亮点之一.数列的交汇综合问题,以数列的相关知识为背景或串联点,把相关的数学知识加以合理创新与交汇,类型多样,变化多端,倍受关注.
2 数列与新信息的交汇综合
含“新信息”情境背景的数列交汇综合问题,经常以图表迁移、新运算、新概念、新情境等形式出现.此类问题与新信息相关,变化形式多样,要运用的相关知识隐藏比较深,破解的关键是找到解题的方向,借助数列的相关知识来分析与处理.
例1如图1,是某省从1月21日至2月24日的新冠肺炎每日新增确诊病例变化曲线图.
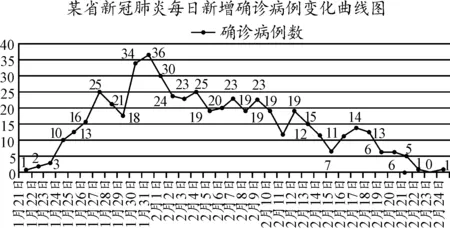
图1
若该省从1月21日至2月24日的新冠肺炎每日新增确诊病例数按日期顺序排列构成数列{an},{an}的前n项和为Sn,则下列说法中正确的是( ).
A.数列{an}是递增数列
B.数列{Sn}是递增数列
C.数列{an}的最大项是a11
D.数列{Sn}的最大项是S11
解析:因为1月28日的新增确诊病例数小于1月27日的新增确诊病例数,即a7>a8,所以{an}不是递增数列,所以选项A错误;
因为2月23日新增确诊病例数为0,所以S33=S34,所以数列{Sn}不是递增数列,所以选项B错误;
因为1月31日新增确诊病例数最多,从1月21日算起,1月31日是第11天,所以数列{an}的最大项是a11,所以选项C正确;
数列{Sn}的最大项是S35,所以选项D错误.
故选择答案:C.
点评:以新情境为问题背景,结合数列的变化曲线图,利用图表迁移,数形结合,根据具体的数据建立相应的数列,并结合通项、求和、数列性质等来分析相应的说法的正确性问题.
3 数列与函数的交汇综合
数列与函数的交汇综合问题主要包括:(1)借助函数条件来解决数列问题,一般利用函数的图象与性质来研究数列问题;(2)借助数列条件来解决函数问题,一般利用数列的取值范围、公式、求和方法,结合式子进行化简变形来研究函数问题.
例2(多选题)定义在(-∞,0)∪(0,+∞)上的函数f(x),如果对任意给定的等比数列{an},{f(an)}仍是等比数列,那么称函数f(x)为“保等比数列函数”.现有定义在(-∞,0)∪(0,+∞)上的如下函数,其中是“保等比数列函数”的为( ).
A.f(x)=x3B.f(x)=ex
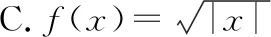
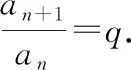
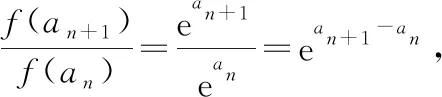
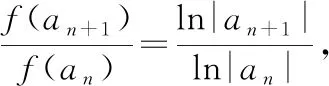
故选择答案:AC.
点评:以创新函数定义为问题背景,结合数列与函数的交汇综合来设置问题,借助函数的解析式,通过等比数列的定义与性质,对比创新定义逐一剖析,进而判定是否满足对应的创新定义问题.
4 数列与不等式的交汇综合
数列与不等式的交汇综合问题主要包括:(1)研究数列中项或前n项和的最值,一般利用数列的单调性来解决;(2)研究数列与不等式的交汇融合,一般通过分解、转化为数列与不等式单独的问题,各自利用相关知识点来解决.
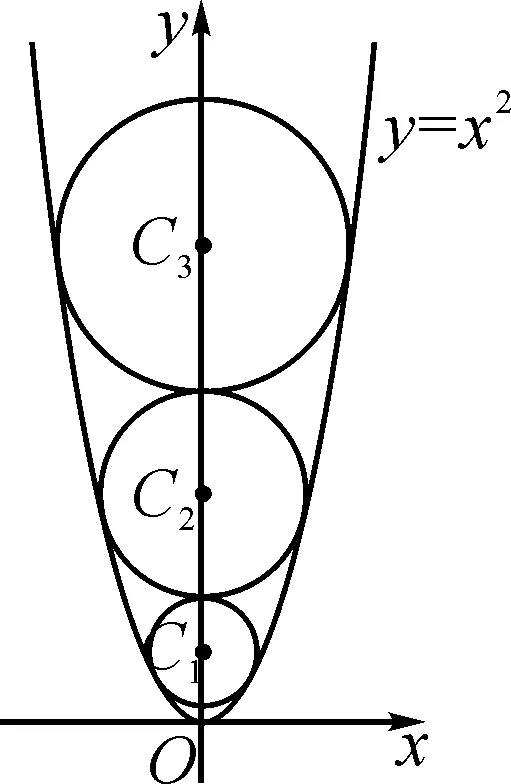
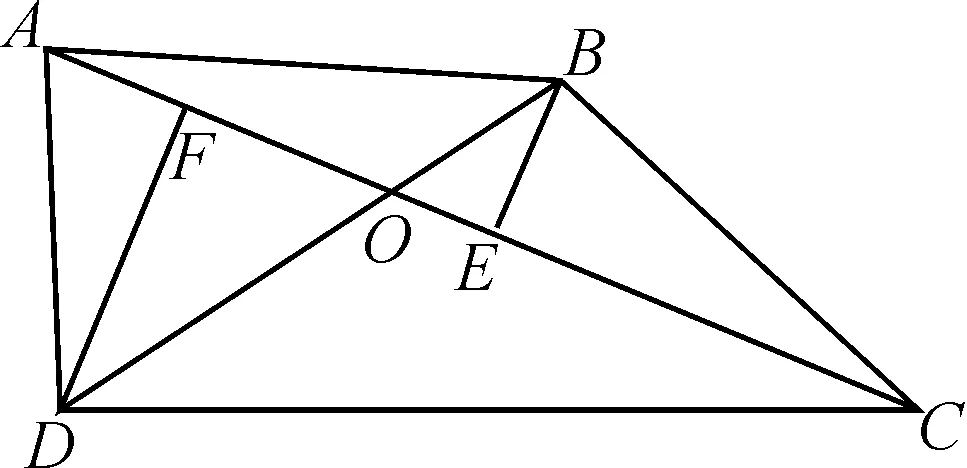
例3已知Sn是等差数列{an}的前n项和,设bn=anan+1an+2,若S7 A.6 B.7 C.8 D.9 解析:由S7 设等差数列{an}的公差为d. 由于a8+a9+a10>0,即3(a1+8d)>0,可得a9>0.又a9+a10<0,则知a10<0,所以d<0. 所以等差数列{an}是递减数列,且a7>0,a8>0,a9>0,a10<0. 所以b1>0,b2>0,……,b7>0,b8<0,b9>0,b10<0,b11<0,…… 由于b9+b8=a9a10(a11+a8),a11+a8=a9+a10<0,a10<0,a9>0,所以b9+b8>0,即当Tn取得最大值时,n=9. 故选择答案:D. 点评:以等差数列的前n项和对应的不等关系式为问题背景,通过求和公式的转化建立相应的不等式组,通过不等关系式的变形与转化,确定数列的单调性与最值,进而确定数列的项数问题. 数列与解析几何的交汇综合,经常借助解析几何曲线上点的坐标关系等来探究数列的递推关系式问题.破解的步骤是:①分析曲线上点的坐标满足的条件;②探究数列的递推关系式,并进行检验. 图2 解析:当r1=1时,圆C1:x2+(y-a1)2=1. 将圆C1的方程与y=x2联立,消去x,得y2-(2a1-1)y+a12-1=0. 由图可知当n≥2时,an=an-1+rn-1+rn. ① 将x2+(y-an)2=rn2与y=x2联立,消去x,得 y2-(2an-1)y+an2-rn2=0. ② 点评:以平面解析几何为问题背景,通过曲线与圆的相切,结合函数与方程思维的应用,代入消参,建立对应的方程,并利用判别式的建立与转化来确定数列的递推关系式,进而结合数列的相关知识来分析与处理. 数列与平面向量的交汇综合问题往往是把数列的项或前n项和渗透在平面向量的线性运算或坐标运算中,利用向量满足的条件转化得到数列的递推关系式,进一步解决数列的相关问题. A.31 B.33 C.63 D.65 解析:如图3所示,连接BD,设AC与BD交于点O,过点B作BE⊥AC于点E,过点D作DF⊥AC于点F.因为△ACD的面积是△ABC的面积的2倍,所以DF=2BE. 图3 所以 an+1-3=2(an-2), 即 an+1-1=2(an-1). 因此,数列{an-1}是首项为a1-1=2,公比为2的等比数列,an-1=2×2n-1=2n,则an=2n+1,从而a5=25+1=33. 故选择答案:B. 点评:以平面几何图形为问题背景,结合平面几何的相关知识、平面向量的线性运算等加以分解与展开,巧妙转化并确定平面向量的相关参数,建立数列的递推关系式,为数列的进一步分析与求解提供条件. 数列与其他知识的交汇综合问题,一直都是历年高考数学中的重点所在与熟悉面孔,巧妙通过数与形的结合,沟通不同数学知识之间的关联,增加数学之间的交汇与综合,提升问题的趣味性与拓展性,增强创新意识与创新应用,提升数学能力,提高数学品质,培养数学核心素养.5 数列与解析几何的交汇综合
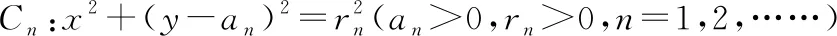
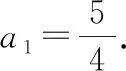

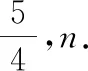
6 数列与平面向量的交汇综合
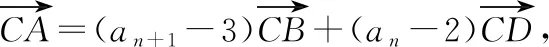
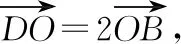

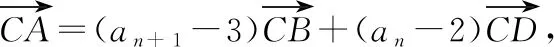
7 结束语
