浅析数学分析课堂教学与思政元素的融合

郭 金 生

（河西学院数学与统计学院，甘肃 张掖 734000）

1 引言

习近平总书记在全国高校思想政治工作会议上强调做好高校思想政治工作，要因事而化、因时而进、因势而新.要遵循思想政治工作规律，遵循教书育人规律，遵循学生成长规律，不断提高工作能力和水平.要利用课堂教学这个主渠道，加强思想政治理论课的建设，努力提升思想政治教育水平，满足大学生的成长需求，并要求其他各类课程与思想政治理论课同步进行思想政治教育，提高学生的素养，促进教育水平［1］.

数学分析作为高等学校数学专业的核心基础课，具有课时多、学分重和覆盖面广等特点，是学习其它分析类课程的基础，贯穿了大学生的整个求学生涯［2］，所以对数学专业的学生而言，学好数学分析课至关重要.依据教学质量国家标准的要求与新的教学理念，将数学分析课堂教学与思政教育更好的结合起来，是当前数学分析创新课堂改革的要求.教师在深入探索数学分析教材内容的基础上，可以充分考虑其课程思政元素，不断改革和创新数学分析的教学方法和教学策略.培养学生积极的学习热情和良好的学习态度，改变数学专业一年级学生学习数学分析困难的现象，并促使学生形成健全的思想观念和完美的人生追求目标，使学生自觉学习数学知识，积极主动地进行数学推导的思维训练，在学习上不断的探索和创新，更深刻的理解和认识数学分析这门课程［3］.

因此，深刻挖掘数学分析课程的思政教育资源，充分发挥数学分析课程中蕴含的思政元素，在教学中积极进行思政教育，达到全方位育人局面和由点带面的育人效果［4］是极其重要的.

2 “数学分析”课程思政教学的讨论和实例分析

2.1 以国内外数学家的优良品格与卓越成就激发学生的学习兴趣，塑造学生良好的品质

中西数学史中蕴含着丰硕的数学文化，它们既是开展数学教育的有用资源，更是思想政治与数学分析结合的融通剂.华东师范大学数学系编写的教材“数学分析”中出现了许多著名的数学家，比如泰勒、莱布尼茨、拉格朗日、柯西、麦克劳林、牛顿等，他们为现代数学的发展做出了杰出的贡献，成为一个个伟大的数学大师，使微积分有了成熟的经典理论基础.此外，还有，中国当代的一些数学家，如丘成桐、陈省身、苏步青、华罗庚、陈景润等，同样为数学做出了突出的贡献.基于此，教师上课可以适当利用几分钟时间来介绍数学家陈景润的生平.陈景润年少时爱数学，爱思考，不惧贫穷饿肚子，为他走向成功的数学道路打下坚实的基础.他的严谨态度和锲而不舍的探索精神，为其研究打下了更为坚实的基础，他时时顽强钻研创新，孜孜奉献，成为每个人学习的榜样.充分利用伟大数学家的详实生平和卓越成就的教育素材，激发学生学习“数学分析”的热情，激励同学们要学习伟大的数学家、杰出的科学家孜孜不倦、勤奋探索的科研精神.每个大学生都需要珍惜求学的大好时光，迎难而上学知识、渐长本领，力争做一个有用的人才，积极服务于社会和国家.

2.2 认真备课，熟悉教材内容，发掘重要的思政教育元素融入数学分析课堂

培养具有综合素质的人才，所有的教师都需要上课时不仅要传授专业知识，也要教给学生做人的方法和道理.因此，作为“数学分析”的任课教师，在教学中应该尽量对学生积极进行道德教育，将做人的道理和处事的态度一并告诉给学生.

例如，数列极限

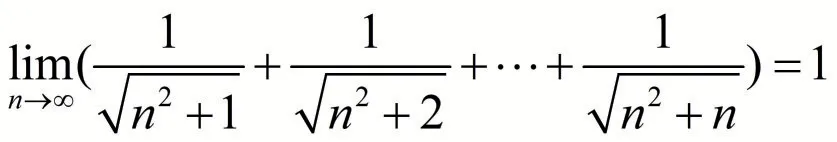
每一项的极限都是零，而此数列极限不为零，实际上虽然有限个无穷小之和仍为无穷小，但无穷多个无穷小的和就不一定是无穷小.在日常生活中，常说蚂蚁搬泰山，反映出量变达到质变的辩证关系，即量变是质变的前提和基础准备，没有量的积累，就无法实现质变，同时质变也是量变的必然结果，即量变必会带来质变，世界上任何的运动和发展都是量变和质变的辩证统一.教育学生在日常学习中要从一点一滴做起，从小事做起，慢慢积累，到大四毕业时，总会有一定的收获.

又如，定义在闭区间[a,b] 上的连续函数f(x)（图1），函数f(x)在闭区间[a,b] 上存在极值，而极值反映了函数的局部状态变化，每个人生活不是一帆风顺的，有时可能会处于人生的低谷，就像函数f(x)在x1处取到极小值，但此时不要放弃自己，一定要努力拼搏，才可能会达到人生的一个高峰.也正像函数f(x)在x2处取到极大值，由于各种不利因素的存在，导致生活有所波动，但要迎难而上，就会进一步达到人生的又一个高峰.其实，每个人的人生曲线是凹凸不平的，如果是一马平川，那就显得太平淡无味了.就像这里的函数f(x)在闭区间[a,b] 上凹凸不平，形成一段完美的曲线.在教学中，需要告诉学生，考入大学并不是终点，让他们不要放松自己，教师要经常提醒学生并鼓励学生，抓住大学的宝贵时间，不断学习，不断进步，勇于创新，不断拓宽自己的知识面，提高学习能力，达到一个新的人生高峰.否则，如逆水行舟，很容易进入学习的低谷，达到了人生的一个极小值点.

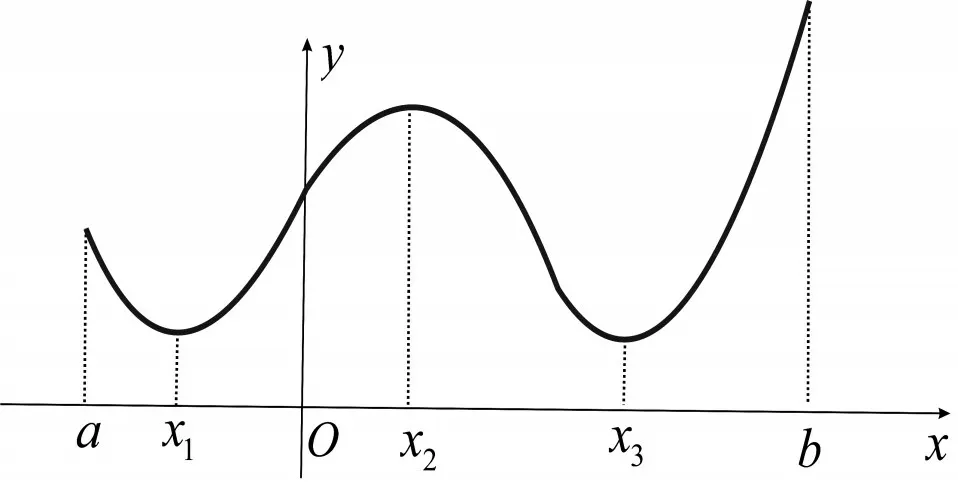
图1 闭区间[a ,b] 上的连续函数f(x)

另外，不管是定积分、二重积分、三重积分、曲线积分还是曲面积分的概念，都是“分割，近似求和，取极限”的思想，其中主要是用到了“以直代曲”，也就是把复杂问题想办法简单化，得到最好的结果.因此，教师要积极引导学生思考，碰到困难时不要把问题想得太复杂，在必要时处理问题要化繁为简，就可能把复杂棘手的问题解决了.教育学生要想在学业上有所成就，必须多下功夫，要有持之以恒、迎难而上的精神，更要有灵活的处理问题的能力.在学习或工作中，思考问题有时也需要直接简单，不需要过于复杂的考虑问题，否则适得其反.又比如和人交流的时候，尽量学会用简洁的语言表达复杂的事，这样可以大大提高效率避免误会，更容易和别人交流.

可以举例数列极限的定义：设{an} 为数列，a为定数，若对任给的正数e，总存在正整数N，使得当n＞N时，有 |an-a|＜e则称数列{an} 收敛于a，定数a称为数列{an}的极限.数列极限的定义虽然简短，对于初学者理解起来很有难度，但其精准的刻画了数列的极限定义，使极限思想贯穿了整个数学分析的内容，借助极限分析研究了函数的各种形态.同样，在生活中就需要用简单方法解决复杂问题，并能直观、准确地解决问题，就是大家共同追求的目标.

2.3 不断创新课堂教学方式，融入思政教育元素，逐渐提高数学分析教学效果

数学分析课堂上，大多数教师采用的都是传统的“注入式”教学模式，学生总是被动的接受知识，几乎没有适当的思政元素渗透，这样的课堂大多数是枯燥无味的，学生接受知识比较慢，在思想上也很难得到深化.在平时的教学中，学生只要能听懂60%的内容，就算听课的效果很不错.在新时代，教师要根据学生生活经历和认知特点，探索新的教学方法和教学手段，让思政元素进入课堂，就要深入研究教材，对课程内容进行适当调整、重新组合和加工，设计让学生去亲身体验、理解和探究，最后感悟，保证课程目标达到要求，不但使学生对课程内容有新的认识，能更好的掌握知识，最重要的是学生有了责任心和良好的人格品质.在正确的思想政治观念和远大的人生梦想指引下，可以激发学生前进的动力，激活数学分析课堂教学的更多积极能量，让数学分析课程中的思政元素拥有更全面、更深刻的师生互动，实现共同进步.例如，通过求高阶导数的方法举例，将每一次求导看成人生中的一次挫折，要教育学生，在面对挫折和困难时不应像函数xn，求一次导降一次阶，那样被挫折磨灭了战胜困难的意志，磨掉了人生的理想，而应该像函数ex那样，不管怎么求高阶导数总是它本身，不忘初心、坚定信念，百折不挠，始终坚持自己的理想，勇敢地面对困难，战胜挫折，最终实现自我人生价值.

3 小结

“数学分析”作为一门专业性极强的核心基础学科，蕴含着丰富的哲理，需要任课教师不断探索.在数学分析课程的教学中，根据国家人才质量培养目标，在合理有效思政评价机制的保障下，教师要充分挖掘蕴含在课程中的思政资源，充分发挥数学分析课堂教学的主渠道，积极探索新的教学方法，将思政元素恰当地融入数学分析课堂教学之中，实现学生学习数学分析课程知识与思政教育相统一的目的.要教育学生不断探索和创新，帮助学生树立正确的人生观和价值观，努力培养出全面发展的社会主义建设者和接班人.