机器人系统摩擦力矩和摩擦模型参数自适应有限时间估计与仿真

方月明，王 娴

(昆明理工大学 机电工程学院，云南 昆明 650000)

机器人在生产制造中具有较高的效率和良好的性能，在工业系统中获得了广泛应用。但随着高精密加工的发展和生产需求的提高，工业系统对机器人的控制精度提出了更高的要求。机器人系统中包含摩擦[1]、死区[2]、迟滞[3]等非光滑动态，影响了机器人系统的控制性能，甚至导致系统不稳定[4-6]。因此，对摩擦等非光滑动态进行准确建模具有重要意义，也是机器人研究领域、学术界和工业界共同关注的焦点问题之一。

随着摩擦学研究的不断深入，研究人员已提出多种摩擦模型来描述各种摩擦特性，例如库仑特性、粘性耗散、Stribeck特性等[7]。在不同的摩擦动态中，库仑模型、静摩擦模型和粘性摩擦模型[8-11]等静态摩擦模型因具有较为简单的内部构造，被广泛用于基于模型的摩擦补偿算法。文献[11]结合了Stribeck效应、库仑模型和粘性项，提出了应用最广泛的经典静摩擦模型。但在需要高精度低速跟踪条件下，该类模型参数确定较难，因此上述经典静摩擦模型具有局限性。研究人员又提出了动摩擦模型，例如Dahl[12]，LuGre[13]和Lueven[14]模型。这些模型虽然可以较好地描述物体在低速下的动态性能，但它们是不连续或分段连续的，给后续的摩擦模型辨识和摩擦补偿控制带来了较大的挑战。文献[15]提出了一种连续可微的摩擦模型，为摩擦模型的参数辨识提供了新的可能。

在系统建模中，参数辨识一直是确定模型参数的有效方法。文献[16]基于库仑粘性摩擦模型使用时域和频域两种方法对其进行了参数辨识。文献[17]针对机床加工精度低的问题使用经典模态分解和最小二乘对Stribeck模型进行了参数辨识。文献[18]基于广义Maxwell滑动模型建立线性压电马达驱动系统的摩擦模型，分别针对滑动阶段和预滑阶段的相关模型进行参数辨识和模型校验。文献[19]在通过泰勒展开对Stribeck模型进行线性化处理之后使用最小二乘法对其进行参数辨识。文献[20]使用改进的布谷鸟算法自动调整判定概率和步长的数值来对连续摩擦模型进行辨识。文献[21]使用连续摩擦模型和径向基神经网络联合建模，通过设计前馈补偿控制器进行摩擦补偿控制。以上方法基于不同摩擦模型，采用参数辨识方法均可对摩擦模型中的参数进行有效辨识。但以上研究在对机器人系统进行建模时，一般需要用到机器人关节或输出轴的加速度信号，这在实际系统中难以满足。特别是将摩擦模型与机器人系统动力学方程相结合实现摩擦建模时，还面临摩擦力矩不可测的问题。

基于以上分析和作者前期的工作[22-24]，本文针对机器人系统摩擦建模的迫切需求，提出一种基于参数估计误差信息的有限时间估计算法来估计一类连续摩擦模型中的关键参数。首先通过对机器人系统模型进行重构避免了加速度信号的使用；再通过设计一个未知系统动态估计器实现对摩擦力矩的准确估计；在获得摩擦力矩的基础上，构建基于参数估计误差的自适应率实现对摩擦模型中关键参数的估计。该方法可迅速并准确地实现摩擦模型关键参数的估计，具有良好的稳定性和鲁棒性。

1 系统描述

含有n个自由度机器人动力学方程可描述为

(1)

为实现摩擦动态精确建模，研究者曾提出不同的摩擦模型，例如经典静摩擦模型、Dahl模型、LuGre模型等，大多含有非光滑动态算子和非线性参数化算子，提高了模型参数估计的难度。为克服该问题，本文采用新近提出的连续可微摩擦模型来描述摩擦力矩F。

F=

(2)

2 未知摩擦力矩估计器

(3)

其中，D∈n，H∈n是不含加速度的向量。机器人系统重构为

(4)

(5)

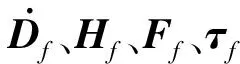
(6)

将式(6)的第1个计算式带入式(5)中可得

(7)

引理1考虑式(4)中的系统和式(6)表述的滤波操作，对任意滤波常数k>0，变量β=(D-Df)/k+Hf+

0。

证明由式(4)和式(6)可计β关于时间的导数为

(8)

选取李雅普诺夫函数Vβ=βTβ/2，可得

(9)

上述引理给出了变量(D，Df，Hf，τf)到未知摩擦力矩F的一种映射关系。用于设计未知摩擦力矩F的估计器为式(10)。

(10)

(11)

(12)

由上可知，将式(1)描述的机器人系统重构为式(4)并引入滤波操作，所设计的未知摩擦力矩估计器避免使用加速度信号，并对摩擦力矩F实现了精准估计。该估计器仅有一个参数(滤波常数k)，该参数选择需考虑鲁棒性和收敛性的平衡。设置过大的k将在估计器引入相位延迟，设置过小的k将导致估计器对噪声的过度敏感。

3 摩擦模型有限时间参数估计

本节将设计自适应参数估计算法实现对式(2)描述的摩擦模型中关键摩擦参数γ1j、γ4j、γ6j的估计。为方便算法设计，本文考虑非线性化参数γ2j、γ3j和γ5j已知，故式(2)被写为如下线性参数化形式

(13)

回归矩阵为

(14)

θ=[α1…αj…αn]T∈3n

(15)

为待估计摩擦模型参数向量，其中的一般项αj=[γ1jγ4jγ6j]。

(16)

为实现未知摩擦参数的准确估计，定义回归矩阵P∈3n×3n，Q∈3n和向量W∈3n为

(17)

式(17)的解为

(18)

从式(17)和式(18)可验证Q=Pθ。由此可知

(19)

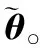
(20)

其中，Γ>0是一个常数对角学习增益矩阵。

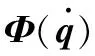
引理2若回归矩阵Φ满足持续激励条件，则矩阵P是正定的(即存在一个常数σ，使得其最小特征值满足λmin(P)>σ>0)。

证明详细证明可参照文献[24]。

(21)

根据上述分析，可知参数误差收敛速度取决于学习增益Γ和持续激励水平σ，故可选择较大的学习增益Γ和较高的激励水平σ以实现更短的时间收敛。

4 鲁棒性分析

本节将针对含干扰的机器人系统，对所提出的未知摩擦力矩估计器和有限时间自适应参数估计算法进行鲁棒性分析。考虑含干扰的机器人系统，其动力学模型为

(22)

其中，ξ∈n是有界的干扰，满足‖ξ‖≤ε，ε>0。

考虑式(3)、式(4)和式(6)，未知摩擦力矩估计器可重新表达为

(23)

其中，ξf是干扰ξ通过滤波器1/(ks+1)之后的向量。故估计误差可表达为

(24)

其在时域可写为

(25)

证明过程与定理1类似，在此省略。

在获得摩擦力矩估计值的基础上，摩擦模型的线性化形式为

(26)

辅助矩阵P和Q定义如式(17)所示，故参数误差信息向量W为

(27)

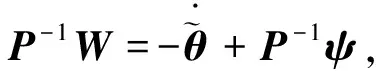
(28)

(29)

5 仿真和比较

在本节中，将采用2自由度的SCARA机器人模型来验证所提出的未知摩擦力矩估计器和参数估计算法的有效性，并将其与多种参数估计方法进行比较，以验证所提参数估计算法的优越性。该2自由度的SCARA机器人的机械结构简图如图1所示，其动力学方程由拉格朗日方程推导得出[26]。

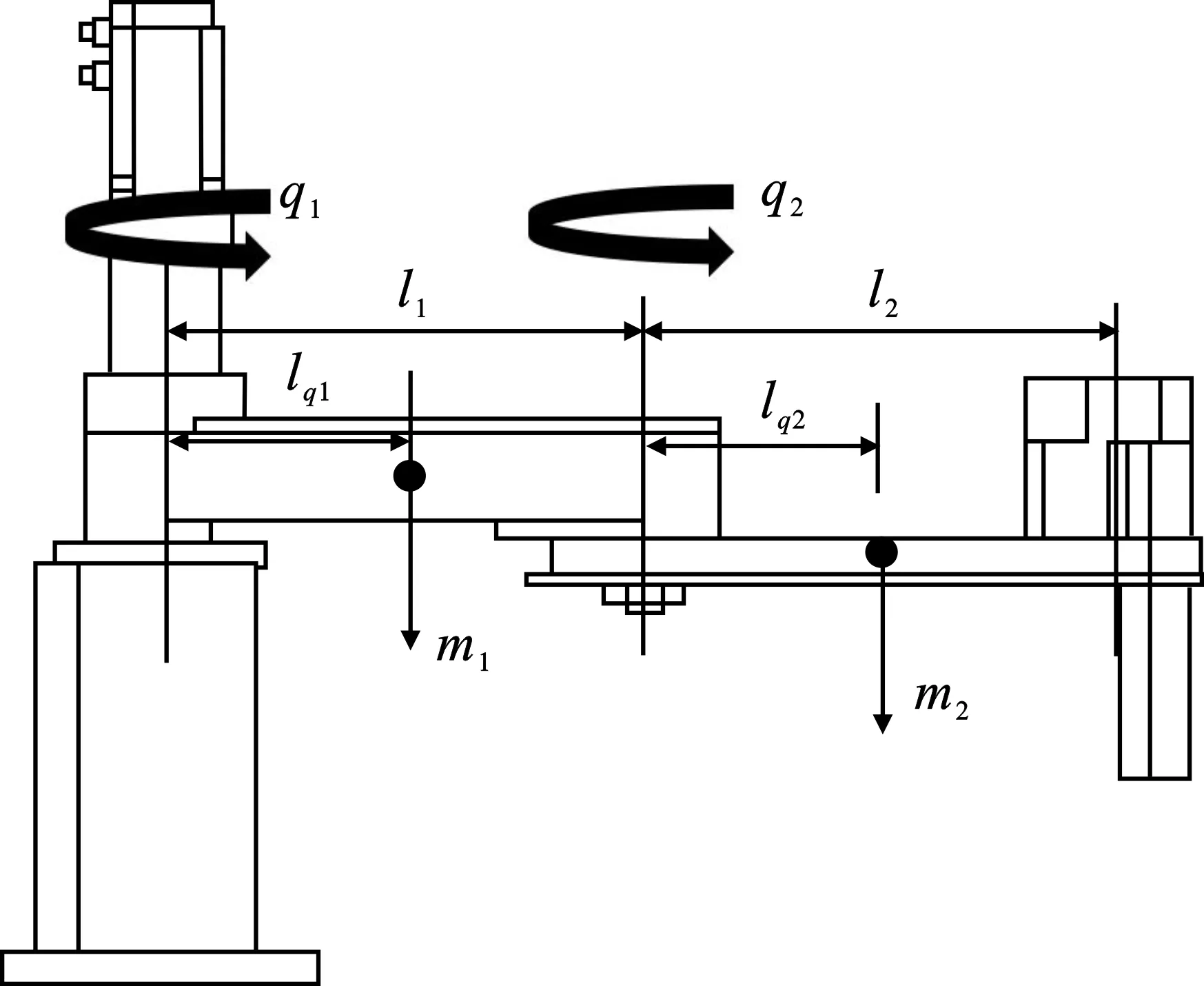
图1 2自由度SCARA机器人机械结构

SCARA机器人的惯性矩阵为

(30)

其中

(31)

科里奥利/离心力矩阵为

(32)

由于SCARA机器人的两个关节仅在XY平面内转动，可忽略重力势能的作用，即

G(q)=0

(33)

假设机器人两个关节摩擦动态相同，该机器人的物理参数和摩擦模型参数在表1中列出。

表1 SCARA机器人物理和摩擦参数

SCARA系统的摩擦模型可表达为

(34)

其中

(35)

(36)

为保证持续激励条件，使用比例积分微分(Proportion Integral Derivation，PID)控制使机器人的两个关节分别跟踪目标位置qd1=πsin(0.2πt)/2和qd2=sin(0.4πt)，PID的参数选择为Kp=800，Ki=60，Kd=30。未知摩擦力矩估计器的滤波系数为k=0.001。摩擦力矩估计结果如图2所示。

图2 未知摩擦力矩估计结果

在获得摩擦力矩估计的基础上，进一步验证摩擦模型并进行参数辨识。为验证所提出的参数估计算法的优势，下面将采用3种传统的参数估计方法与之进行对比。

首先，定义预测输出摩擦转矩和估计摩擦转矩之差为预测误差，记为e，即

(37)

(1)梯度下降法[27]。梯度下降法由预测误差e驱动

(38)

其中，Γ>0是学习增益；

(39)

其中，σ>0是正常数。

(40)

为公平比较，给定相同参数估计初始条件。式(17)所示的有限时间自适应参数估计算法中的参数选为=1.5，κ=100，和Γ=20diag(100，1，1)。图3给出了多种参数估计算法的对比结果。

图3 各类参数估计算法的对比

图4 摩擦特性的对比

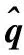
图5 输出对比图

由上述结果可知，本文所提出的参数辨识方法可实现机器人系统摩擦动态的精确建模，进而保证了机器人的跟踪效果。

6 结束语

本文提出一种未知系统动态估计器来对机器人系统中的摩擦力矩进行在线估计，并开展一类新型摩擦模型关键参数辨识。为避免使用加速度信息，本文提出了低通滤波对机器人系统进行重构，进而设计可确保快速收敛的未知摩擦力矩估计器。在获得摩擦力矩估计值的基础上，引入一种自适应参数估计算法实现对摩擦模型中关键摩擦参数的有限时间估计。将基于SCARA机器人模型的仿真结果同多种参数估计算法结果进行对比，结果表明本文所提的未知摩擦力矩估计器和自适应参数估计算法可准确快速地实现摩擦模型参数估计，有效实现摩擦动态的精确建模。