星载转台活动电缆扭转阻力矩测试与分析
2022-01-07费志禾李志慧陈雅璐牛科研夏振涛
费志禾,李志慧,陈雅璐,牛科研,夏振涛
(上海卫星装备研究所,上海 200240)
0 引言
随着卫星功能的不断提升,星载转台成为部分型号的重要部件。卫星系统的小型化要求转台结构紧凑、轻便灵活,而功能提升又导致其内部电缆数量急剧增加[1-2]。电缆的可靠性和使用寿命是影响转台机构可靠性和寿命的重要因素之一[3-4]。电缆随机构转动会发生扭转和弯折,产生扭转阻力矩。而长时间扭转和弯折易导致电缆绝缘层磨损破裂,甚至造成导线短路、断路等严重后果;同时,扭转阻力矩的稳定性也严重影响转台控制的精度。因此,降低控制电缆的扭转阻力矩对于星载转台的寿命延长和可靠性提高具有重要意义。
目前卫星上使用的低频电缆未将导线抗反复扭转、弯折性能列入其性能验证项目。为保证低频电缆的可靠性,一方面要求供应商提高导线的抗反复扭转、弯折性能,另一方面需定量分析电缆阻力矩的影响因素,通过合理的布线设计,优化电缆布局[5-6]。国内外学者针对低频电缆布线提出了很多方法和建议,但针对电缆扭转阻力矩的定量分析相对较少。袁新江等[7]根据阻力矩基本测量原理,对小型机载雷达天线座的电缆阻力矩进行测试,研究阻力矩受低温及电缆走线方式影响的程度。黄业平等[8]对低温环境下射频电缆扭转阻力矩进行测试,并依据测试结果对展开锁定机构进行设计改进,改进后机构的展开时间、冲击力矩等指标满足卫星总体要求。高燕飞[9]对电线电缆在扭转情况下的应力应变情况和导体的轴向应力响应开展2D 扭转试验,并进行疲劳特征分析,从初始角、螺旋线螺距等5 个变量对电缆接触面应力进行优化设计。上述研究均针对单根电缆进行阻力矩测试,并改进布线结构;而对于多束活动电缆扭转阻力矩变化规律的定量研究还未见报道。活动电缆两端固定形式,电缆束分布状态、使用工况、环境条件均会对电缆扭转阻力矩产生影响,而如何通过控制活动电缆扭转阻力矩实现高可靠、高稳定、长寿命的电力与信号传输是目前星载转台亟待解决的问题。
某型号星载转台采用低频电缆代替导电滑环实现电力和信号的传输,以满足传输数据量大、传输精度高的要求。因此需要一种能解决扭转阻力矩高度非线性和相对不可控问题的电缆布线方案,以保证转台机构正常平稳运转。本文针对该型号星载转台活动电缆扭转阻力矩进行测试与分析[10-11],依据转台工作状态设计扭转阻力矩测试装置,探究不同工况下扭转阻力矩的变化规律,考查不同运动状态下扭转阻力矩的稳定性,验证通过小线束、分布式布线方案降低活动电缆扭转阻力矩的可行性。
1 扭转阻力矩测试
1.1 试验对象
某型号星载转台共包含不同种类电缆导线110 余根,转台电缆扭转阻力矩要求控制在2 N·m以内,电缆转动寿命要求200 万次以上。为满足上述要求,采用小线束、分布式的布线方案,将导线均匀分为8 个直径不超过12 mm 的线束,对称布置以减小重力对扭转阻力矩的影响。如图1 所示,为保护活动电缆不受空间环境影响,线束从空心轴轴孔中走线;线束两端通过轻型电缆支架固定在轴法兰和端盖边缘,两固定端之间为活动电缆部分,随着机构转动发生扭转和变形。线束外套锦纶丝套管,并适当松垂以防止转动过程中绷紧。转动轴和端盖在±48°范围内相对转动,即活动电缆从初始状态扭转至最大转角位置时线束的扭转角度为48°。该转台的工作模式主要为连续转动和固定指向保持,本文根据转台实际工作状态和要求,对其电缆布线方案产生的扭转阻力矩进行测试和分析,试验电缆导线由湖南华菱线缆公司提供。

图1 星载转台电缆布线示意Fig. 1 Cable wiring for satellite turntable
1.2 试验设备
采用高精度扭转试验机进行电缆扭转阻力矩测试[12],该设备的扭矩分辨率为0.001 N·m,测试范围为10 N·m。测试过程采用转角控制模式实现转轴的转动角度与角速度控制,并实时测量运动阻力矩。转轴和端盖分别固定在扭转试验机的两端,通过三爪卡盘实现同轴安装,经测量,二者的装配同轴度为0.17 mm。试验开始时,旋转主轴使半轴和端盖的中心面对齐,调整初始位置转角为0°。
1.3 扭转阻力矩测试方法
电缆扭转阻力矩的主要影响因素有转动速度、位置和环境温度等。依据转台设计要求及工作状态,本文主要研究转动速度和运动路径对电缆扭转阻力矩的影响。测试环境温度为10℃,气压为常压状态,设定试验机主轴左旋为正,试验状态如图2所示。分别进行以下测试:1)连续转动模式下,电缆连续转动扭转阻力矩测试;2)固定指向模式下,电缆保持在不同位置时的扭转阻力矩测试;3)固定指向模式下,电缆从不同位置启动的扭转阻力矩测试。

图2 电缆扭转阻力矩测试试验状态Fig. 2 State of cable resistant moment testing
2 测试试验结果与分析
2.1 连续转动扭转阻力矩变化规律

表1 不同角速度下电缆扭转阻力矩最大值Table 1 Maximum of cable resistant moment at different angular velocities
由图3 还可看到:正向转动时扭转阻力矩随转角增大而增大,且增加速率逐渐变大,反向转动时扭转阻力矩曲线呈阶梯式下降;角速度为0.1 (°)/s时,阻力矩曲线随转角增大过程中出现较多毛刺,而角速度较大时阻力矩曲线相对光滑。这主要是由于转动角速度较小时,线束内部导线有足够的时间发生相对滑移和变形,使阻力矩在上升过程中发生小的突变,即表现为阻力矩曲线产生毛刺。
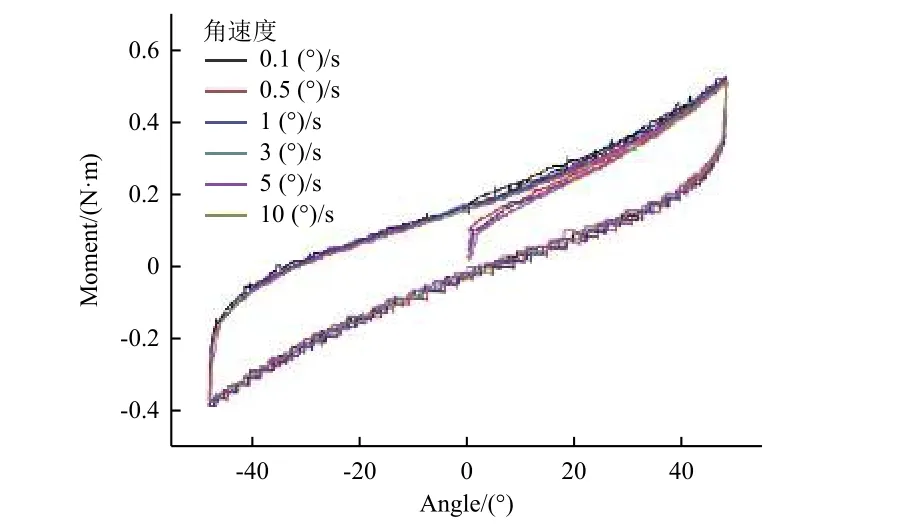
图3 不同角速度下电缆扭转阻力矩随转角变化曲线Fig. 3 Curves of cable resistant moment at different angular velocities
角速度对扭转阻力矩的影响基本可以忽略,故可假设在相同的环境下,同一束电缆的扭转阻力矩仅与转角相关。扭转阻力矩可以分为线性φ1(θ)和非线性φ2(θ)两部分,当线束满足小变形假设和平面假设时,扭转过程中线束横截面保持平面状态,且形状、大小、两横截面间距均不改变。φ1(θ)可表示扭转阻力矩与转角间的线性关系;φ2(θ)表示电缆自身其他因素对扭转阻力矩的影响,包括初始不平衡力矩、内部结构变化等。采用多项式函数进行拟合,[-40°,40°]范围内的扭转阻力矩表达式为M=φ1(θ)+φ2(θ)=0.273θ+0.046θ2+0.155θ3+0.165;拟合曲线如图4 所示。可以发现,在转角较小时,表达式中的二次项和三次项可忽略不计,扭转阻力矩随转角变化基本满足线性变化关系;也表明转角较小时,线束内部未发生滑移和变形,基本满足小变形假设和平面假设,与实际试验情况相符。

图4 扭转阻力矩随转角变化拟合曲线Fig. 4 Fitting curve of cable resistant moment against the twisting angle
电缆在±48°范围内往复运动过程中,电缆的扭转阻力矩发生周期性变化,呈迟滞回线状态。图5为电缆扭转阻力矩和转角随时间周期变化曲线。若不考虑两侧电缆重量和截面惯性矩的差异,则扭转阻力矩变化应具有对称性。测量初始不平衡扭矩约为0.144 N·m,对阻力矩曲线进行对称处理得到红色的曲线。从图中可以发现,阻力矩曲线与转角曲线具有相同的周期和相位,但转角零位相对于阻力矩零位滞后。当转角为0 时,扭转阻力矩约为0.1 N·m,当扭转阻力矩为0 时,残留的电缆扭转角约为20°。

图5 电缆扭转阻力矩和转角随时间周期变化曲线Fig. 5 Cycles of cable resistant moment and twisting angle over time
2.2 保持在不同位置时扭转阻力矩变化规律
固定指向模式下,分别将电缆以3(°)/s 的角速度扭转至15°、30°、45°、90°、180°的位置后,保持静止120s,再以相同的角速度恢复至零位。图6 为电缆保持在不同位置时扭转阻力矩随时间变化曲线。可以发现,电缆在保持静止状态下发生卸载,阻力矩呈阶梯式下降。在转动至180°的过程中,阻力矩曲线产生了尖点和毛刺,当阻力矩达到1.65 N·m 时陡然下降,而后随着转角的增大继续升高,整个加载过程中阻力矩呈曲折式上升。说明当阻力矩达到一定值时,电缆内部导线会发生变形和滑移,以释放内部应力,则造成阻力矩突然下降,同时内部结构的改变速度随内部应力的减小而不断减缓。

图6 电缆保持在不同位置时扭转阻力矩随时间变化曲线Fig. 6 Curves of cable resistant moment over time at different cable positions
2.3 从不同位置启动的扭转阻力矩变化规律
固定指向模式下,测试电缆从不同位置启动时电缆扭转阻力矩随转角的变化,结果如图7 所示。将电缆以3 (°)/s 的角速度扭转,转动过程中分别在不同位置保持静止10 s 和30 s 后重新启动。对比可见,保持静止30 s 相对于保持静止10 s,阻力矩卸载产生的曲线毛刺更明显。从曲线上可以看出,任意位置重新启动,阻力矩都不超过连续转动过程中相同位置的阻力矩,即任意位置启动,阻力矩仍然控制在连续转动阻力矩曲线的包络内。这个结果对提高控制系统稳定性具有重要意义。
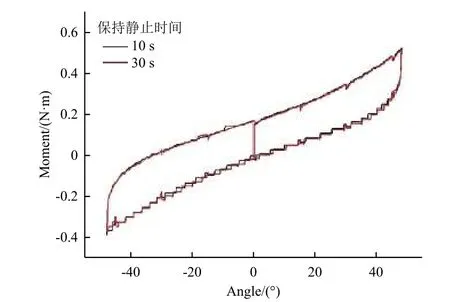
图7 不同位置启动时电缆扭转阻力矩随转角变化曲线Fig. 7 Curves of cable resistant moment vs. angle for different start positions
固定指向过程中,阻力矩变化瞬间包括静止瞬间、启动瞬间和复位瞬间,静止瞬间指转台转动至固定角度停止的瞬间,启动瞬间指从固定角度继续增加转角的瞬间,复位瞬间指从固定角度快速回到零位的瞬间。假设瞬时变化速率为1°范围内扭转阻力矩变化的平均速率,转动角速度3 (°)/s。不同位置扭转阻力矩的瞬时变化速率可表示为dM/dt=(dM/dθ)×(dθ/dt),扭转阻力矩瞬时变化速率见表2。可以看到,在不同位置停止转动,阻力矩瞬时变化速率可忽略不计;启动瞬间和复位瞬间的阻力矩瞬时变化速率均随转角增大而增大;阻力矩瞬时变化速率可以满足控制系统精度要求。
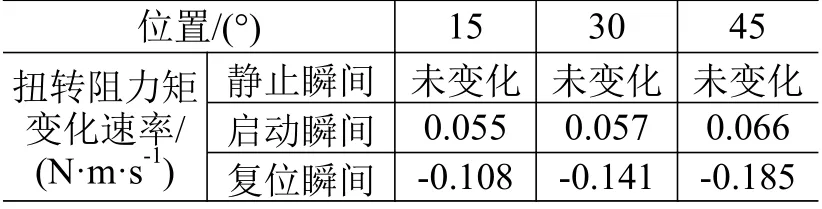
表2 不同位置的扭转阻力矩变化速率Table 2 Variation rate of cable resistant moment at different positions
3 结论
本文针对基于小线束、分布式布线方案设计的星载转台活动电缆进行了扭转阻力矩测试和分析,定量分析了阻力矩影响因素,总结了不同工况下阻力矩变化规律。得到以下结论:
1)扭转阻力矩随转角增加而增加,扭转角速度对阻力矩的影响基本可忽略;
2)扭转阻力矩随转角周期性变化,转角零位相对阻力矩零位滞后约20°;
3)在保持静止状态下,电缆阻力矩呈阶梯式下降,可能是内部导线滑移变形造成的阻力矩卸载突变;
4)任意位置重新启动,扭转阻力矩仍然控制在连续转动阻力矩曲线的包络内;
5)静止瞬间、启动瞬间和复位瞬间电缆阻力矩瞬时变化速率满足控制系统精度要求。
本文验证了小线束、分布式布线方案可有效减小电缆扭转阻力矩,提高阻力矩稳定性,满足卫星型号要求,是后续星载转台布线设计的可选方案。
