从双重差分法到事件研究法
2022-07-13黄炜张子尧刘安然
黄炜 张子尧 刘安然







关键词:因果推断;双重差分法;事件研究法;实证研究
一、引言
随着计量经济学“可信性革命”(credibility revolution)席卷經济学的各个领域,基于潜在因果模型的因果效应识别策略,如匹配法(matching)、工具变量法(instrumental variable)、双重差分法(difference-in-differences)和断点回归设计(regression discontinuity design)等,逐渐成为了经济学等社会科学领域实证研究的通行研究范式。上述几种方法的使用要求和适应场景各不相同,双重差分法由于其直观清晰、易于理解,并且实际操作难度较低、上手简单等特点而广为应用。图1展示了中文期刊经济管理类学术论文各类方法的使用数量变化,可以看到自2015 年后使用双重差分法的国内经济管理类研究数量急剧上升,在2019 年超越工具变量法成为了目前使用最为广泛的计量方法,并且其上升趋势仍有进一步加强的倾向。由此或可推测,在未来的一段时期内,双重差分法仍然将是经济管理类实证研究的主流方法之一。
双重差分法在实证研究中主要用于评估政策效应。与其他方法相比,双重差分法的识别方法非常直观:先观察受政策影响的个体在政策前后的变化,再观察未受政策影响的个体在政策前后的变化,两个变化之间的差异就是政策干预对个体的影响。同时,双重差分法可以非常方便地使用最小二乘法来实现。直观理解加上简单易行使得双重差分法得到了广泛应用,学者们使用双重差分法评估了许多重要的政策效应,例如,刘瑞明和赵仁杰(2015)发现国家高新区的建设显著地促进了地区经济增长;吕越等(2019)发现“一带一路”倡议促进了中国企业海外绿地投资;Liu 和Mao(2019)发现增值税转型改革显著提高了企业投资并改善了生产率;宋弘等(2021)发现社保法定费率下降使得企业社保缴费参与率提高,但削弱了企业的劳动力需求。以上文献只是大量使用双重差分法实证研究中的沧海一粟。
然而,伴随着双重差分法的广泛使用,一些对于双重差分法的不精确理解甚至是错误认识也逐渐开始出现。常见的一些问题包括:双重差分法的基本识别假设是什么?双重差分法需要政策是完全随机分配的吗?平行趋势假设是什么?通常所说的平行趋势检验真的是在检验平行趋势假设吗?控制变量应该如何选取?什么样的变量必须控制,什么样的变量必须不能控制,什么样的变量可以控制也可以不控制?当政策干预时点不一致时双重差分法应该如何实现?这种实现方法有什么问题,应该如何改进?等等。实证研究者在研究过程中或多或少都曾遇到或将要遇到上述问题,但是标准的计量经济学教材中很少直接回应这些实践方面的疑问,研究者不得不根据自身的理解来处理上述问题,这是对双重差分法产生不正确理解的原因之一。基于此,本文结合国际上关于双重差分法的最新研究,试图对双重差分法应用中的一系列问题进行初步探讨,希望能够帮助廓清一些疑惑,为我国经济学界研究与国际前沿接轨提供些微贡献。
本文的结构如下:第二部分描述双重差分法的计量实现,对研究中常用的几种双重差分法进行归纳总结,而后着重强调了双重差分法的识别假设及其直观含义。第三部分分析双重差分法使用中的控制变量选取、平行趋势检验的实现和理解,以及组间线性时间趋势是否控制三个常见易混淆的问题。第四部分讨论了近年来广泛应用的交错双重差分法的实现和潜在问题,以及如何尝试使用动态双重差分法和事件研究法来克服交错双重差分法的不足。第五部分讨论了双重差分法评估政策效应时常见的几个问题,包括需要重视真实的制度背景、政策干预是否需要完全随机、溢出效应以及一般均衡视角下的成本收益分析。最后是总结性评论。
二、双重差分法的计量实现和识别假设
(一)标准DiD(standard DiD)
双重差分是一种尝试采用控制组实际未经处理的结果变化作为处理组倘若未经处理的结果变化的反事实来分析因果效应的方法,通常包括冲击事件、处理组、控制组和时期这四个要素,其经典构造可以表示为如下形式:
双重差分的核心是通过构造交互项来识别政策冲击对受影响个体(处理组)的平均处理效应(average treatment effect on the Treated,ATT),①即基于一个反事实框架来评估政策冲击发生与不发生这两种情况下处理结果it Y 的变化。真实的因果效应需要通过比较处理组接受处理与不接受处理的状态得出,然而在现实生活中,当冲击发生后,我们仅能观察到处理组受到冲击后的情况,无法真正知晓其未受冲击的情况。而在双重差分方法中,控制组提供了一个可供研究的反事实,即可将未受到处理的控制组在观察时期内的“变化”近似于处理组倘若未受到冲击将发生的变化。从处理组前后时期的变化中减去控制组前后时期的变化,即可得到因果效应 。上述分析的数学表达式如下式所示,第一个中括号内为处理组前后时期的差分效应,第二个中括号内为控制组前后时期的差分效应,两个一次差分再相减后,得到双重差分处理效应:
(二)双重差分法的其他形式拓展
1. 交错双重差分法(staggered DiD)。标准双重差分法模型和双向固定效应双重差分法模型涉及的政策实施时点或冲击发生时点为同一时期。然而,现实生活中诸多政策实施未必发生在某一时点,而是先有试点再逐步推广,在渐进的过程中推而行之,如增值税转型、土地确权、新农保实施、高铁修建等。交错双重差分法为处理这类情形提供了方法。②当个体接受政策冲击的时间不同时,政策分组虚拟变量i D 变为it D ,此时it D 即可用来表示个体i 在时间t 处是否受到政策冲击,而无需再生成交互项。不过在实际应用中,交错双重差分法可能会遇到难以找到控制组、部分样本始终为处理组、异质性处理效应等问题。由于交错双重差分法适用面较广且使用时又有诸多需要注意的事项,本文将在第四部分详细讨论这一方法的应用与利弊。
2. 广义双重差分法(generalized DiD)。当所有研究对象均或多或少同时受到了政策干预,即仅有处理组而无控制组时,仍然能够考虑应用双重差分法。对此,可以根据研究对象受到的具体冲击情况来构建处理强度(treatment intensity)指标来进行分析,此时个体维度并不是从0 到1 的改变,而是连续的变化。因此,可以将个体维度的政策分组虚拟变量替换为用以表示不同个体受政策影响程度的连续型变量,该种方法被称为广义双重差分法。①Nunn 和Qian(2011)研究了一个经典的例子,他们研究了土豆种植扩散对欧洲人口增长的影响。欧洲几乎所有地区都种植了土豆,不存在未种植土豆的地区,因此没有标准意义上的控制组。他们的选择是将地区间土豆种植适宜度作为处理强度,以1700 年前后为处理时点,使用广义双重差分法估计了引入土豆对人口增长的影响。
3. 队列双重差分法(cohort DiD)。队列双重差分法也被称为截面双重差分法,即使用横截面数据来评估某一历史事件对个体的长期影响。队列双重差分法同样是比较两个维度上的差异大小:一个维度为地区间差异,标识该地区是否受干预政策影响或干预强度;另一个维度为出生队列间差异,标识个体是否受到了干预政策的影响。队列双重差分法本质上是使用未受政策干预的出生队列作为受到政策干预的出生队列的反事实结果。Duflo(2001)是早期应用队列双重差分法的经典研究,近年来使用这一方法的代表性文献有Chen 等(2020)的研究文献。
4. 模糊双重差分法(fuzzy DiD)。在标准双重差分法等方法的应用情境中,处理组和控制组之间通常泾渭分明,因此可以通过分组差分得到较为“干净”的处理效应。但是,有时冲击并未带来急剧(sharp)变化,所谓的“处理组”中虽然受冲击率高于其他组别,但并没有完全被干预或受政策冲击,而所谓的“控制组”中也并非完全没有受到冲击,即处理组和控制组之间没有明确的分野,不存在“干净”的处理组与控制组。模糊双重差分法为处理此类情形提供了可能,de Chaisemartin和d’Haultfoeuille(2018)在文章中详细介绍了该种方法,并利用该方法重新评估了印度尼西亚的教育回报。
5. 三重差分法(triple differences)。顾名思义,三重差分法引入了第三个维度“组别”(group),通过比较不同组别间的处理组和控制组在干预政策前后结果变量变化的差异来识别因果效应。②三重差分法的应用场景通常有两个:一是在平行趋势假设不满足时引入第三个维度的差分来帮助消除处理组和控制组间的时间趋势差异;二是在平行趋势满足时,用于识别干预政策在不同群体间的异质性处理效应。三重差分法是一个典型的实践先于理论的方法,其使用最早可以追溯到Gruber(1994),近年来在顶级期刊使用越来越频繁,不过直到Olden 和Møen(2020)才较为完整地讨论了三重差分法的识别假设和使用条件。
6. 其他双重差分法。纵观上述各种类型的双重差分法,其基本思路是寻找观测样本在两个维度上的差异,其中一个维度用于控制不可观测的时间趋势,另一个维度用于测度政策效应的变化。
如果从更加一般化的角度理解双重差分法背后的直觉和思想,可以发现事实上几乎任何两个维度的差异之差异都可以从双重差分的角度去理解。也就是说,几乎所有的交互项模型都可以理解为一种双重差分法。一个典型的例子是Mayzlin 等(2014)的研究,他们研究了造假成本对在线旅店预定网站的消费者评论的影响。两家在线酒店预订网站中,Expedia 网站只有实际完成订单的消费者可以评价服务质量,而TripAdvisor 网站则是任何人都可以评价服务质量,所以两个网站的造假成本是不同的。他们发现,当一家旅店周围没有其他旅店存在时,该旅店在TripAdvisor 上的好评率显著高于在Expedia 上的好评率,这是因为该旅店试图操纵评论提高本店评分。当一家旅店旁边存在另一家邻近的旅店时,该旅店在TripAdvisor 上的差评率显著高于Expedia 上的差评率,这是各旅店试图打压竞争对手,为对手恶意评低分。他们的识别策略事实上和双重差分法不谋而合:Expedia 和TripAdvisor 的造假成本构成了一个维度差异,旅店邻近范围内是否存在直接竞争者构成了另一个维度的差异,通过二者之差就能够识别出造假成本对网站消费者评论操纵的影响。①另一个例子是Rajan 和Zingales(1998)的研究,该研究试图论证金融发展对经济增长的影响。他们使用的一个识别策略是交互项模型:被解释变量是k 国j 行业的增长率,解释变量是j 行业的外部融资依赖度和k 国的金融发展程度的交互项。其背后的直觉如下:若金融发展确实能够促进经济增长,那么j 行业的外部融资依赖度越高,金融发展对其经济增长的激励越强。因此,如果不同行业间的外部融资依赖程度差异(第一个维度)和金融发展水平的跨国差异(第二个维度)能够解释不同国家行业间的增长率差异,就能够论证金融发展对经济增长的影响。②
(三)双重差分法的识别假设
双重差分法的应用需要满足一定的假设条件,倘若违背了这些前提假设,估计结果可能会严重偏离真实的因果效应。本部分对双重差分法的识别假设内容及可能违背假设的情景、后果进行讨论。
1. 平行趋势假设。双重差分法最基本的假设是平行趋势假设(parallel trend assumption),又称共同趋势假设(common trend assumption),是指倘若处理组个体未接受干预或冲击,则其结果变动趋势与控制组个体结果变动趋势相同。该假设数学表达如下:
由上述分析可知,双重差分法要求在没有干预或处理的情况下,处理组和控制组的平均结果随时间变化的趋势相同。该识别假设可以记为更简便的形式:双重差分法背后隐含着“准自然实验”的思想,并不严格要求处理组与控制组之间满足随机分组条件。实际上,双重差分法所要求的“随机分组”,是指结果变量的变动趋势独立于政策冲击,即关于Y 0满足随機分组条件。需要强调的是,这一识别假设和我们通常所说的随机分组是不同的,一般意义上的随机分组要求处理状态和潜在结果不相关,即(Y0|D=1) (Y0|D=0),显然,该识别假设和双重差分法要求的潜在结果差分意义上的随机分组有区别。假使处理组与控制组满足随机分组原则,那么便近似于随机对照试验(randomized controlled trial,RCT),处理组与控制组的结果对比便是处理效应,无需再使用双重差分法。
这里需要说明一个问题:双重差分法作为一种计量模型,其本身解决内生性问题吗?答案应该是否定的。事实上,双重差分法是一个估计量,更是一种研究设计。作为估计量的双重差分法,估计的是处理组和控制组的结果变量在干预前的组间均值差异和干预后的组间均值差异,即差异之差异。然而,这个估计量是否能够正确识别我们关心的因果效应,取决于识别假设式(2)是否成立。更为严谨的说法是,在满足识别假设的前提下双重差分法能够正确识别因果效应,而式(2)经过简单的变形可以发现,它实际上就是双重差分环境下的外生性假设。所以,作为估计量的双重差分本身并没有解决内生性问题,而是“假设”不存在内生性问题。而作为一种研究设计,双重差分法可以追溯至19 世纪中期物理学家John Snow 对伦敦霍乱成因的研究(Snow,1855),①Card 和 Krueger(1994)关于最低工资的早期研究也采用类似的设计思想。②如果没有研究设计的“双重比对”的想法,是不会产生双重差分法这一估计量的。事实上,是在有了双重对比的研究设计后,我们使用双重差分这一估计量来捕捉所关心的具体的因果效应。然而,当下一些使用双重差分法的实证研究将估计量与研究设计二者等同起来,似乎有了这个估计量,就自然而然有了对应的研究设计,就可以直接避开内生性问题,这是不正确的。双重差分法解决内生性问题,本质上仍然依赖于干预或政策冲击本身的外生性。
从处理组前后两期结果的变化中减去控制组的两期结果的变化,其实质是去除共同趋势的影响,从而得到“干净”的政策效果。需要注意的是,严格来说,共同趋势假设是无法被完全检验的。
文章中的做法通常是检验处理组和控制组的事前平行趋势,然而,冲击发生前变化平行并不能保证今后依然平行。倘若政策冲击并不随机,而是会被某因素X 所影响,那么X 在决定干预是否发生的同时,也很有可能会影响共同趋势的变化。因此,尽管双重差分法不要求处理组与控制组在各方面相似,但如果一些与结果变量相关的预处理特征在处理组和控制组之间不平衡,那么研究对象很有可能不满足共同趋势假设。通常我们仍然希望处理组和控制组之间较为相似,此时可以去检验关键控制变量的差异,或者尝试与匹配方法相结合等。其中,匹配方法可作为非参数估计手段,也可以作为一种数据预处理手段。双重差分法本身近似于一种差分意义上的匹配方法。③倘若处理组和控制组之间存在明显差异,那么通常要选取不同的控制组来进行稳健性检验。此外,如果处理组和控制组在处理前后存在成分变化(compositional changes),这意味着政策可能具有很强的内生性,通常难以满足共同趋势假设,在该种情况下,要慎重使用双重差分法。
双重差分法中除去政策、时间等两个维度的变量外,还可以再加入其他变量进行控制,即在模型中加入控制变量it W 。然而,在实际回归操作中,具体应当加入什么控制变量、哪些变量不能被控制、是否要加入线性趋势等问题需要格外留意。本文将在第三部分对此展开讨论。
2. 单位处理变量值稳定假设(SUTVA)。单位处理变量值稳定假设(stable unit treatment valuesassumption,SUTVA)是指不同个体是否受到政策冲击是相互独立的,某一个体受政策冲击的情况(treatment status)不影响任何其他个体的结果。直观理解,不满足SUTVA 意味着控制组个体也受到了干预政策的影响,因而不再是事实上未受干预影响的“真实”控制组,也就无法使用控制组时间趋势来构建处理组时间趋势的反事实。在理想情况下,处理组和控制组被严格区分开来,彼此互不干涉,然而,在现实生活中,相当多的政策冲击具有一定的外部性,例如加强上游省份水污染企业的环境督查也会有利于改善下游省份水质。此外,个体的行为也往往具有一定的策略性和选择性,如处理组地区得到了较好的政策帮扶,那么原本控制组地区的个体可能会自发从控制组地区迁移至处理组地区,意味着宏观上非政策目标地区也受到了干预政策的影响,这就是通常所说的一般均衡效应(general equilibrium effect)或溢出效應(spillover effect)。一般均衡效应或溢出效应会使得SUTVA 不再成立,进而导致双重差分法无法正确识别因果效应。Butt(s 2021)在Callaway和Sant’Anna(2020)研究基础上采用事件分析法对这类溢出情况进行了处理。
三、双重差分方法中需要注意的具体问题
(一)控制变量
在回归方程中加入控制变量起到两个作用。第一,保证条件独立假设(conditional independenceassumption,CIA)成立。①条件独立假设成立意味着给定控制变量时处理变量i D 与误差项it 不相关,从而保证了OLS 估计量b 是我们所关心的因果效应 的一致估计。这是观测性研究的因果推断中控制变量所发挥的最核心作用。第二,减小误差,提高估计精度。如果处理变量i D 与误差项it 已经不相关,无论是否加入控制变量,b 都是因果效应 的一致估计。此时加入合理的控制变量可以降低误差从而提高估计精度。
Cinelli 等(2021)将控制变量分为三类。第一类控制变量是为了保证CIA 成立而控制的变量(称为好控制变量,good control),必须在回归方程中加以控制。由于这类变量既影响it Y 又影响i D ,不控制这类变量会导致明显的“遗漏变量”问题,从而使得OLS 估计系数b 不是因果效应 的一致估计,这是观测性实证研究面临的最大挑战。以常用的面板数据为例,首先,通常个体固定效应和时间固定效应必须加以控制,其次是既影响it Y 又影响i D 的可观测变量it X 。不过这里需要强调的是,发生在处理时点之后( D t≥T )的 it X 作为事后变量,很有可能是一个“坏”控制变量(见下文),对其加以控制会导致估计系数b 不一致。为了避免这类问题,一般的做法是控制事前某一后者可以控制更为灵活的时间趋势形式,因而在实践中更为常用。
第二类控制变量是可能导致CIA 不成立的变量(称为坏控制变量,bad control),必须排除在回归方程之外。受到i D 影响的结果变量一般都是坏控制变量,加入回归方程会使得估计系数b 不再具有因果解释力。坏控制变量问题可能对因果效应的估计产生极大的影响,图2 是一个模拟估计的例子:添加了合理控制变量的双向固定效应模型能够很好地估计真实因果效应,然而一旦继续加入坏控制变量,估计系数会产生极大的偏误。判断控制变量是否合理的一个经验法则是考虑控制变量的决定时间:在处理时点之后产生变化的变量都可能受到i D 的影响,很可能是坏控制变量。①在过去相当长一段时期内有一种看法认为“凡是与it Y 和i D 相关的变量均应该作为控制变量纳入回归方程”,这种看法忽略了坏控制变量的存在。对控制变量的选择直接决定了实证研究的可信性,需要研究者更加谨慎地对待。②
第三类控制变量是不影响CIA 是否成立的变量(称为中性控制变量,neutral control),在回归方程中可加可不加。从因果效应识别的角度而言,这类变量是否加入回归方程并不影响对因果效应估计的一致性,控制或不控制均可。从统计推断的角度来看,合理地控制这类变量有助于减小残差从而提高估计精度,但是与坏控制变量问题类似,选取不当的中性控制变量反而会使得估计偏误增加。判断中性控制变量是否应该控制的一个经验法则是:影响被解释变量it Y 的中性控制变量可以加入回归方程中以减小误差,提高估计精度;影响i D 的中性控制变量一般不控制,因为若控制则会减小Di Tt的变动性(variation),降低估计精度。
(二)平行趋势与事前趋势检验
平行趋势(parallel trend)又称共同趋势(common trend),指处理组个体的it Y 在没有接受处理的状态下拥有和控制组个体it Y 相同的时间变动趋势,它是双重差分法能够正确识别因果效应的前提条件。由于处理组个体在处理时点后的反事实结果(处理组没有接受处理的it Y )无法观察到,平行趋势假设本质上是无法直接检验的。因此,研究者通常退而求其次,通过检验可观察的处理组和控制组事前趋势是否相同来间接地检验平行趋势假设。如果处理组和控制组的事前趋势平行,那么研究者就有一定的信心认为事后趋势也是平行的。
式(3)中的i D 是分组变量, st T 是第s期的时间虚拟变量, pres 和posts可以直观地理解为在处理发生前和处理发生后的第s 期处理组和控制组被解释变量it Y 的差异相对于基期(这里是处理发生前一期)处理组和控制组被解释变量it Y 的差异。①②事前平行趋势满足意味着在处理时点D T 之前的各个时期组间差异没有发生明显变化,因此可以通过检验pres 是否显著异于0 来间接地检验事前平行趋势是否成立。图3 是一个模拟的例子,可以看到在处理发生前各个时期的pres 均不显著,联合检验结果也无法拒绝处理前系数都为0 的原假设,因此可以认为事前平行趋势得到了满足。
式(3)不仅能够检验事前平行趋势,还能够观察到处理效应的动态变化。注意, ts pos 代表了处理时点D T 之后的各个时期组间差异相对于基期的差异,如果处理效应确实存在,我们应该期望得真实因果效应1。因此式(3)实际上发挥着检验事前平行趋势与处理动态效应的双重作用。
需要强调的是,事前平行趋势通过检验并不意味着平行趋势假设一定成立。正如前文强调的,平行趋势假设本身不可检验,而事前平行趋势只是整个平行趋势假设的一部分,即使事前平行趋势通过检验也只是表明处理组和控制组在处理发生前保持相同时间趋势,并不能确保事后趋势也一定平行,所以“事前平行趋势检验通过,平行趋势假设成立”说法并不准确。①
(三)组别时间趋势的进一步分析
使用双重差分法评估政策效应的可靠性依赖于平行趋势假设,因此,在实证研究中最为担心的一点就是干预分配的过程可能使得平行趋势假设不成立。例如研究贫困县政策对经济发展的影响时,由于贫困县依据人均GDP 等经济指标来认定,被划为贫困县的地区经济发展速度很可能原本就比非贫困县更慢,处理组(贫困县)和控制组(非贫困县)之间的经济发展状况很难满足平行趋势。
一个可能的选择是加入组间线性趋势i t D Trend 以控制组间线性时间趋势的差异,从而缓解这一问题。②图4a 给出了数值模拟的证据,当处理组和控制組存在明显的时间趋势差异时,直接使用双重差分法估计出的处理效应存在明显偏误,但控制组间线性时间趋势后就能准确地估计处理效应。事实上,根据上述的分析,在双重差分法中额外地控制住组间线性趋势可以作为一种稳健性检验:若平行趋势假设满足,那么是否加入组间线性时间趋势不会对估计结果产生明显影响;反之,若估计结果发生了明显改变,则预示着组间时间趋势可能存在差异,平行趋势假设可能并不满足。
然而,控制组间时间趋势也是一把双刃剑,可能会产生一些不合意的后果。第一,组间线性时间趋势i t D Trend 和双重差分的核心解释变量 i t D Post 的构造方式相似,因此二者存在比较明显的共线性,控制组间线性时间趋势会大大减少核心解释变量的变动程度从而降低估计效率、提高标准误。从图4a 中可以发现加入线性时间趋势后的估计系数分布明显更加分散,这表明估计量效率降低、标准误变得更大了。第二,如果处理效应不是一次性的,而是随着时间推移逐步显现出来,那么组间线性时间趋势会吸收一部分处理效应,导致双重差分法会低估真实效应。图4b 的模拟结果说明了这一点:在处理效应存在动态变化时,加入组间线性时间趋势会大大低估真实的处理效应。因此,是否控制组间时间趋势需要研究者结合具体的研究情景仔细斟酌。
从本质上看,组间时间趋势存在差异的根本原因是存在某些可观测或不可观测的前定变量在处理组和控制组之间存在差异或者是存在随时间变化的混淆因素。比如前面提到的贫困县的例子,贫困县和非贫困县的经济发展趋势差异是由当地的初始经济发展水平、地理条件、文化等一系列因素综合造成的。对于可观测的因素,可以通过添加控制变量的方法加以控制,但对于不可观测的因素则一般很难直接处理,通过控制组间线性趋势差异可以部分缓解这一问题,然而当组间时间趋势差异和动态处理效应同时存在时也无法完全解决这一问题。针对这种复杂情况,目前主要有两种处理思路。一种思路是在双重差分的框架下,通过使用未受处理的样本来更为干净地估计和剔除掉时间趋势。①另一种思路可能需要超越双重差分法,寻找工具变量或使用空间断点回归设计等方法,不过这些问题超出了本文的范围,这里不再加以讨论。
四、动态双重差分法和事件研究法
(一)交错双重差分法
在标准的双重差分法中处理组在同一个时间点受到干预,然而现实中有相当多的政策并非是一次性全面实施,而是先在某些地区试点后再分批逐步推广,处理时点并不一致。一个典型的例子是增值税转型改革:2004 年7 月首先在东北地区开始试点,2007 年7 月扩大至中部6 省,2008 年7 月推广至内蒙古以及汶川地震受灾地区,2009 年1 月1 日起覆盖全国。标准的双重差分法并不适用于这样的政策。一个常用的方法是交错双重差分法(staggered DiD),“交错”一词表明该方法适用于干预时点有前后差异的政策。交错双重差分法的回归方程设定为如下形式:
(二)从动态双重差分法到事件研究法
动态双重差分法可以被视作交错双重差分法的动态效应检验。与标准双重差分法检验动态效应的基本思路一致,也是通过检验处理组和控制组在干预前和干预后的组间均值差异变化来识别政策的动态效应。与标准双重差分法不同的是,在干预时点交错发生的情境下无法定义一个绝对的时间参照点作为处理前和处理后的分界线。因此,动态双重差分法不再以绝对时间为参照系,而是以干预发生时点作为相对时间参照系(图6)。动态双重差分法的计量方程设定形式为:
那么,一个自然延伸出的问题是,既然可以使用当期未受处理但在未来会受到处理的处理组个体作为控制组,那么是否可以在没有从未接受处理的控制组样本的情形下使用动态双重差分法?答案是可以,这种情形就是经典的事件研究法(event study)。事实上事件研究法在公司金融、资产定价等领域的应用要远早于双重差分法,早期的代表性文献有Fama 等(1969)的研究。事件研究法的计量模型设定为
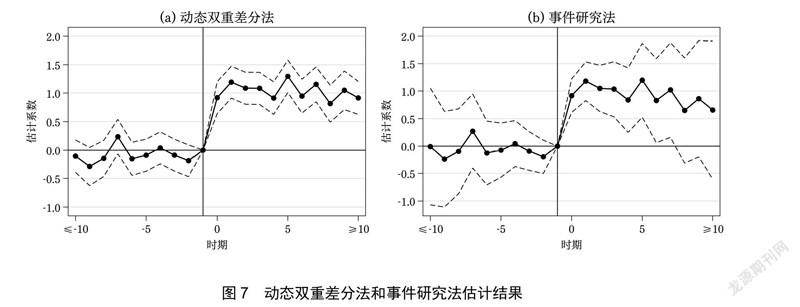
式(6)中的符号定义与式(5)相同。比较式(5)和式(6)可以发现二者本质上是一致的:如果所有个体都会受到处理(但处理时点不同)、没有从未受到处理的控制组,那么样本中全部观测值的i D 都等于1,式(5)就会变化为式(6)。因此,事件研究法本质上可以近似为去除了控制组的动态双重差分法。图7 使用了同一组模拟数据分别应用动态双重差分法和事件研究法,可以看到两种方法的系数估计结果几乎完全一致,只不过由于事件研究法剔除了控制组样本使得样本量偏小、估计系数的标准误更大。从计量方法的发展历程看,事件研究法出现的时间要更早,动态双重差分法是事件研究法在样本包含未接受干预的处理组情形下的自然拓展。
使用动态双重差分法或事件研究法需要注意事件窗口的选择,这里主要指窗口时间宽度的选择。一般来说,干预交错发生的数据结构涉及到的事件窗口宽度要更长一些。比如若数据集包含10 期的观测值,其中既有第1 期就接受干预的个体,也有到第10 期才接受干预的个体,那么该样本涉及到的窗口宽度为干预前9 期、干预发生当期以及干预发生后9 期,共19 期。①由于窗口宽度大于样本时间跨度,观测值在干预前后各期的分布是不平衡的,一般而言距离干预时点越远的样本越少。不平衡样本可能带来样本选择偏误(selection bias)和样本消耗(attrition)问题的困扰。选择的事件窗口越宽,样本不平衡现象越严重,会愈发加剧上述担忧。此外,事件窗口越长,越有可能受到同时期发生的其他事件和混杂因素的干扰。如果从时间断点(time cut-off)回归设计的角度理解事件研究法,可以将时间视为驱动变量(running variable),一般来说窗宽选择越宽则样本规模越大、估计越有效(efficient),但可能会有更大的偏误(bias)。总体来看事件窗口的宽度不宜过长。由于事件研究法的估计结果对事件窗口的选择较为敏感,在实际研究中通常需要更换事件窗口宽度来做一些稳健性检验。目前,学界仍在不断完善这一方法,Sun 和Abraham(2020)、Borusyak等(2021)的研究围绕事件分析法中的异质性处理等问题进一步进行了拓展与讨论。
五、双重差分法研究中的其他问题
(一)制度背景和政策实施真实情况
双重差分法应用最多的场景是评估政策效应。对于制度背景的清晰梳理和政策真实实施情况的正确观察应该是政策评估类实证研究的基石。一项政策可能发布了却没有很好地实施,也可能受政策影响的个体采取了“上有政策,下有对策”的策略式行动影响了政策实施真实效果,如果研究者没有很好地厘清这些制度背景和政策实施的真实情况,就不可能准确地评估政策效应,甚至可能得到误导性的研究结论。
这里举一个实例。相当多的研究发现地方政府的财政补贴相当低效,企业获得了大量的财政补贴却并没有激励企业的研发创新能力,甚至会引起企业寻租(王红建等,2014;张杰等,2015)。然而,范子英和王倩(2019)通过对地方政府税收征管实务的观察,发现财政补贴实施过程中存在相当明显的“列收列支”问题:地方政府为了增加名义上的税收收入,会先向企业多征收一部分税款,再以财政补贴的名义返还回去。所以,相当一部分名义上为财政补贴的资金实际上是企业自有资金,而这部分“虚假”的财政补贴自然不会对企业经营行为产生影响。因此,财政补贴的低效率很可能是由于对政策实施真实情况的把握不够深入导致的错误结果。总体而言,使用双重差分法评估政策效应要求对政策的具体实施情况有深入、清晰的了解:政策什么时候开始真正实施?政策是否按照要求得到了准确执行?行为主体是否采取了一些应对措施?等等。这一系列问题与双重差分法是否合理、可行程度密切相關,也是进一步深入分析政策机制效应的良好开端。因此,政策评估类的实证研究有必要高度重视制度背景和政策实施情况。
(二)干预政策需要严格外生或随机分配吗?
在第二部分双重差分法的识别假设部分,我们强调了双重差分法本身并没有解决内生性问题,而是“假设”干预政策是外生,内生性问题的解决仍然依赖于干预政策本身的外生性。然而,这里的外生性是什么意义上的外生性?换言之,双重差分法下需要干预政策和谁之间是外生的?一种看法认为干预政策必须是完全随机(自然实验)或者近似随机分配(准自然实验),即干预政策和模型未考虑的所有因素(扰动项)之间不相关,只有在这种情况下才适用双重差分法(陈林和伍海军,2015)。但是,现实中的任何一项政策几乎都有特定的政策目标和政策对象,完全随机分配的政策几乎并不存在,那么这类政策是否完全不适用双重差分法呢?本文认为并非如此。第二部分对识别假设的讨论清楚地表明,双重差分法所需要的外生性是干预政策和扰动项在差分意义上的外生性,这与水平意义上的外生性显然并非是等价的。①
我们以贫困县政策的经济发展效应评估为例。水平意义上的外生性要求贫困县名额的分配过程要近似完全随机,无论是贫困地区还是富裕地区都有差不多的机会入选贫困县,显然这并不符合现实——贫困县的选取标准主要是人均GDP、人均财政收入等指标,被选为贫困县的地区都是经济发展十分落后的县域,因此贫困县政策并不满足水平意义上的外生性。但是,差分意义上的外生性是有可能满足的,即贫困县可能和非贫困县有相同的经济发展趋势。如果研究设计能够尽量满足这一识别假设,就可以使用双重差分法。例如黄志平(2018)的做法是首先使用倾向得分匹配法(PSM)对数据预处理,在非贫困县中尽量选取与贫困县的各方面禀赋条件类似的控制组,从而尽可能地使得平行趋势假设成立(等价于差分意义上的外生性),而后使用双重差分法估计因果效应。
(三)溢出效应
双重差分法的另一个核心识别假设是SUTVA,即干预不存在一般均衡效应或溢出效应。然而,现实中的各项政策几乎或多或少都会存在一定的一般均衡效应,例如前文提到的上游省份加强水质环境规制会影响下游省份水质的例子。特别是在长期中,当处理组个体的决策发生变化时,控制组个体一定会随之调整自身的行为决策。因此,干预政策是否存在溢出效应是任何一个使用双重差分法的实证研究必须考虑的潜在威胁。
不过,检验溢出效应是否存在并非一项简单的工作,研究者需要根据制度背景仔细识别可能受到溢出效应影响的控制组个体,而后检验溢出效应。Lu 等(2019)研究中国经济开发区对当地经济发展的影响,其对溢出效应的讨论和处理是一个较为成功的范例。他们采取了两种识别策略检验溢出效应,第一种是检验与经济开发区所属村庄邻近的同县其他村庄经济发展是否也得到了提高,第二种是检验经济开发区对经济发展的激励效应是否随着村庄离经济开发区越来越远而减弱。第一种方法的结果表明同县其他村庄的总产出、就业等仅有略微的提高且统计上不显著,第二种方法的结果表明距离经济开发区2 千米之外的村庄基本上不受经济开发区的影响,两种方法都提供了证据表明经济开发区政策的溢出效应并不显著。
还需要强调的一点是,如果研究重点本身就是政策的溢出效应的话,那么是不适用双重差分法的。例如一些研究试图探讨地区产业政策对企业选择效应和集聚效应的影响:本地拥有更加优惠的产业政策(如税收优惠)会吸引相邻地区的企业迁移到本地区,产生选择效应和集聚效应。这里的选择效应和集聚效应就是溢出效应的一个典型表现:本地区的政策对邻近地区的企业产生了影响,因此该话题显然不适合使用双重差分法。研究者需要注意避免类似的问题。
(四)一般均衡视角下的成本收益分析
双重差分法广泛应用于各类公共政策的评估,如果估计得到了政策效应符合预期,是否就意味着政策达到了初始目标或是政策本身就是有效的呢?不是。一般而言,双重差分法只能评估干预政策对研究者感兴趣的结果变量的影响,但研究者并不清楚政策本身的机会成本有多大,也不清楚政策的净收益到底是多少。评估政策效应整体上是否符合预期或是政策是否有效率,并不能仅根据估计结果就判断政策是否有效,而是需要从更广泛的一般均衡角度,从整体上对政策进行成本收益分析。
Duflo(2001)是在政策效用评估类文献中成功应用成本收益分析的早期经典代表,她研究了印度尼西亚修建学校对当地儿童的长期劳动力市场的影响。根据双重差分法的基准结果,她估计了印度尼西亚政府投资学校建设的成本和对儿童未来的工资收益,发现投资学校建设的内部回报率为8.8%-12%,远高于当地实际利率,因此投资教育是一个非常高收益的投资项目。①Lu 等(2019)对中国经济开发区的政策效应同样进行了成本收益分析,他们根据双重差分法的估计结果计算得到2006-2008 年间经济开发区为当地居民和企业提高的工资和利润总额约为1 807 亿元,付出的税收成本则为558 亿元,净收益高达1 249 亿元。上述例子都体现了研究者在一般均衡的视角下,从机会成本和政策收益两个角度对政策效果进行完整的评估。研究者在完成双重差分法的估计后,通常需要对政策进行成本收益分析,在此基础上才能更为完整地回答政策是否达到预期目标、是否有效率等问题,并提供合理、可行的政策建议。否则,若研究者过于关注政策的直接效果而忽略了潜在的政策成本,就可能对政策的整体效果产生错误判断,将整体上无效率的政策判定为有效政策,最终导致错误的政策建议。
六、总结性评论
本文结合近年来国内外关于双重差分法的理论和实证研究文献,系统梳理了双重差分法的基本计量设定、识别假设和双重差分法的各个类型变体,着重分析了双重差分法实际应用中面临的控制变量选择、平行趋势检验和组间时间趋势差异等容易混淆或理解不准确的问题。特别是近年来交错双重差分法逐渐得到广泛使用,但最新的一些理论计量研究成果表明交错双重差分法在异质性处理效应下存在着一系列不合意之处,可能导致错误的因果效应估计结果,因此,本文建议研究者可以考虑使用动态双重差分法或事件研究法来替代交错双重差分法作为基准识别策略和实证结果展示方法。本文详细介绍了动态双重差分法和事件研究法的计量实现以及两者的区别和联系,通过数值模拟方法揭示了二者本质上的等价性。本文还强调了实践中使用动态双重差分法和事件研究法时对窗宽选择的重要性。最后,本文从政策评估实证研究的角度提出了研究者在使用双重差分法进行实证研究时需要注意的几个重要问题,包括重视制度背景和政策真实效应的梳理和确认、对于政策干预随机性的准确理解、重視对溢出效应的处理和讨论,以及从一般均衡视角对政策效应的收益和成本进行全面评估等。
近年来使用双重差分法进行的实证研究呈现爆发式增长,近乎泛滥,但若深究其中,许多研究并没有正确地理解双重差分法基本识别假设和需要注意的问题,产生了各式各样的偏差与错误。并且,许多学术期刊的匿名审稿人也出现了这些错误和问题,使得一些匿名审稿人提出没有意义甚至是错误的修改建议,而论文作者多数时候只能将错就错去迎合匿名审稿人,甚至将原本正确的做法被迫修改为错误的做法,可谓是见笑于大方之家。长期来看这种错误会极大阻碍我国经济学研究与国际一流研究接轨的脚步,产生的伤害不可谓不严重。本文试图对上述错误和问题在一定程度上进行归纳、总结、厘清和解决,如果能对未来的研究者提供一些参考,为我国经济学研究进步提供些微助力,本文的目的就完全达到了。
当然,本文的观点均是由作者从自身的理解和实践经验中提取总结而来,作为一家之言,必定有谬误或不足之处,仅为抛砖引玉。期待后续学界同行的进一步研究,促成我国经济学界的共同进步。
