横向声波扰动下的乙醇燃烧火焰结构和振荡特性

张玉涛，林国铖，史学强，张玉杰，王兴明

西安科技大学安全科学与工程学院，西安 710054

如何实现高效清洁的灭火一直是火灾科学领域的热点问题[1].相对于传统常见的灭火技术，无污染的声波灭火技术近年来逐渐进入学者们的研究视野[2-3].2002年Baillot和Demare[4]研究了2 ～3000 Hz范围内的声波对于扩散射流火焰的影响，结果表明小于50 Hz的声波会显著降低火焰的稳定性；此外，声波对火焰的抑制行为已被证明在微重力状态下有显著的效果，未来可将其推广应用于灭火易造成二次损失的封闭或半封闭场所[5].

关于声波对火焰行为影响的研究最早源自于内燃机和锅炉燃烧引发的热声不稳定现象[6-9]，学者们从改善燃烧效率的角度出发，研究封闭状态下的声波对火焰行为的控制效果：Hakim等[6]和Han等[7]发现燃烧噪声的不同声学模式会导致火焰不稳定振荡，造成局部熄火的现象；Vignat等[8]针对甲烷燃烧器内火焰对声扰动的响应进行了研究，发现当波长与火焰厚度相当时，火焰对声学扰动的敏感性最大，火焰形态和燃烧的延续都会受到影响；Kypraiou等[9]利用平面激光诱导荧光技术（Planer laser induced fluorescence，PLIF）对非预混火焰在振荡声强迫环境下的熄灭条件进行了研究.

在此基础上，近年来已有部分研究从针对封闭环境的声振荡影响衍伸至开放环境声波对火焰的熄灭和抑制，进而研究声波在开放环境下的灭火应用：Xiong等[10]研究了声波对于下落液滴火焰的熄灭效果，并将Damkohler（Da数）作为判定熄灭的标准分析下落液滴火焰的熄灭机制；Zong等[11]实验测试了横向声强迫对射流扩散火焰的抑制效果，发现横向低频声波能明显降低扩散火焰的火焰高度.Friedman和Stoliarov[12]对线形火焰在声波扰动作用下的燃烧行为进行了研究；此外，魏珠萍[13]对蜡烛以及香棒在声波作用下的燃烧特性的研究表明，不同声压级范围的声波对固体扩散火焰的燃烧速率具有促进和抑制的双重作用；Fujisawa等[14]通过纹影技术分析了声波作用下火焰形态的转变过程；Beisner等[5]的研究表明，在微重力状态下声波对火焰的有良好的抑制效果.这些研究为声波灭火的实际运用和机理研究提供了一定的借鉴.

就现有研究而言，声波对于实验室级别的小尺度火焰的熄灭、控制效果已经得到文献证实，但对灭火和抑制火焰的具体尺度范围还未有准确的定义，火焰的具体抑制原理也尚不明晰.同时，常见的固体、液体和气体扩散火焰由于其不同的燃烧特点，在声波强迫作用下的发展特点也不尽相同[15].因此，本文针对油池火焰，研究了3、4和5 cm直径的油池火焰在30～90 Hz频率声波作用下的几何形态、频域分布和火焰特征参数.为声强迫抑制火焰行为的具体条件及声波灭火的应用提供了参考.

1 实验装置

实验设备包括信号发生器、功放、扬声器、测声装置、油池及高速摄像机，实验台布置如图1（a）所示.油池为不锈钢杯，高度均为8 cm，直径分别为3、4和5 cm，燃料为无水乙醇，点燃时液面高度距离油池杯口0.5 cm，环境温度为28 ℃.扬声器直径为30 cm，放置位置距离火焰15 cm，中心正对不锈钢杯口.声波信号为正弦信号，实验频率范围的选取参考已有研究的频率范围[10-14]并结合预实验，结果发现火焰在100 ～500 Hz频率的声波作用下呈现与自然燃烧近似一致的火焰行为，因此选取了 30 ～90 Hz（间隔为 10 Hz）的声波作为实验的频率范围.由于相同的扬声器声功率在播放不同声频率时声压级会存在较大差异，实验通过检测并调节声压级大小的方式使不同声频率下的声压相近.测声装置采用多通道动态信号分析系统（北京声望声电技术公司），声探头布置在油池上方10 cm处，声信号测试在每次点燃火焰前进行，各频率下的声压级如图1（b）所示.高速摄像机型号为台湾衡欣9501，采样频率设定为每秒200帧，分辨率为800像素×600像素，设置在距油池1.5 m处且垂直于油池与扬声器连线，摄像头正对火焰.根据奈奎斯特定理[16]，高速摄像机的帧数及测声装置的采样频率均大于声信号最大频率的2倍，以保证能捕捉火焰与声波耦合作用下的整体信号.

图1 实验装置示意图及声波参数图.(a)装置示意图；(b)声参数图Fig.1 Diagram of experimental system and sound parameters: (a) experimental system; (b) sound parameters

2 结果与分析

2.1 火焰形态

油池火由于重力作用，竖直方向上存在压力梯度，而在水平方向上由于燃烧产生的热气体和环境气体的密度差异而产生密度梯度，两者梯度的不重合导致斜压涡量产生，进而形成涡旋[17].声波扰动会造成火焰在径向方向的密度梯度和压力梯度的不稳定变化，引起火焰面的弯曲变形和火焰涡旋的动态演变，而不同尺度的油池火焰也会呈现不同的形态特征.通过高速摄像机拍摄声波作用下的火焰图像，结果如图2所示.由于火焰形状呈现周期性交替改变，选取每种频率下出现频次最高的火焰形态发展图像序列进行说明.高速摄像机对每组实验拍摄时长为7 ～ 10 s，每张图像的时间间隔为0.005 s.

图2 无声波强迫下与声波强迫下不同直径油池火焰部分火焰图像（左、中、右分别为3，4和5 cm直径油池火焰；a,b,c,d,e序列分别为无声波，30，50，70 和 90 Hz声波）Fig.2 Partial flame images of pool flame under an acoustic force (left, middle, and right pool flames are 3, 4, and 5 cm in diameter, respectively; a, b, c,d, and e sequences are nonacoustic with 30, 50, 70, and 90 Hz acoustic force, respectively)

3 cm直径的乙醇油池火焰在部分频率下的火焰连续图像如图2（左）所示，无声波激励下（a序列）火焰呈现规律脉动的状态，火焰两侧根部出现轴对称侧涡旋结构，逐渐上升至火焰顶部，在火焰末端处脱落，此时涡旋的上升周期时间相对长，这种行为也被称为“膨胀”（puffing）[18]；在30 Hz 和50 Hz声波作用下，火焰向水平方向发生偏转（b序列和c序列）.这是由于侧涡旋的运动使得火焰的垂直动量随火焰高度的增加而增加，因此在火焰根部具有最明显的水平偏转.同时由于火焰在水平方向的偏移，涡旋对的不对称运动抽运了更多的空气和燃烧产物，引起火焰在中部的断裂，造成局部熄火并在水平气流的作用下形成整体截断状态（b8），这与Pretrel等[19]的实验现象一致；火焰在70 Hz与90 Hz（d序列和e序列）声强迫下较为稳定，图像与无声波状态下的火焰相似，但火焰外围轮廓亮度较大，火焰呈现尖、长的特点.由于声波脉动频率的增加影响了水平方向动量的积累，限制了涡旋的尺度，因而在火焰表面形成更多更小直径的涡[20]，促进了空气和可燃物的掺混使得火焰面燃烧更为完全，火焰也更为明亮.

由图2（中）可以看出，与3 cm直径相比，4 cm直径油池火焰由于热释放量的增加，在竖直方向的压力梯度增加，无声波状态下(a序列)的膨胀行为（puffing）更为明显；在30 Hz声频率作用下，与3 cm直径油池火焰类似，火焰在不对称涡旋的卷吸作用下出现横向截断(b序列)；在50 Hz声频率作用下时，火焰在顶部呈现“T”型（c序列），可能是由于声压的正弦交替转变至反方向，引起背声侧涡量的增大，原本在顶端处脱落的涡旋进一步卷吸火焰，使原本依附于火焰轮廓线的涡旋能够引起火焰面的褶皱变形；火焰在70 Hz和90 Hz声波环境下（d序列和e序列），同样处于燃烧较为稳定的状态，亮度也略大于无声波时.

5 cm直径油池的火焰（图2右）在所有实验频率下都不存在明显的横向截断状态，在30 Hz声波作用下，火焰虽然发生偏移和断裂，但与3 cm和4 cm直径油池火不同，燃烧尺度的增加能更快补充被涡旋卷吸而破碎的火焰（b序列）；此外，火焰面积的增加促使沿火焰面移动的涡旋从单一方向的运动向多方向的运动转变（c序列）；火焰在70 Hz和90 Hz声波强迫下不发生偏移，处于稳定燃烧状态，这与3 cm、4 cm直径油池火相似.

由于声波引起的涡旋扰动以及火焰本身脉动不稳定性会引起火焰形态的动态变化，因此当火焰在特定声频率下出现间歇截断的火焰形态时，定义火焰此时为间歇截断状态，该声强迫的频率为间歇截断频率；出现火焰相对于中心轴线的偏转时，则定义为偏转状态；火焰在水平方向上不发生扰动时则为稳定燃烧状态.总体而言，随着声波频率的增加，涡旋逐渐由影响火焰结构的内部区域转移至火焰表面的轮廓线，涡旋直径也逐渐变小，引起的燃烧不稳定性逐渐减弱.此外，3 cm和4 cm直径油池火焰的火焰形态呈现由间歇截断到偏转，再到稳定燃烧的状态，5 cm直径火焰不存在间歇截断频率，火焰形态直接由偏转状态向稳定状态转变；而随着油池直径增加，涡旋移动的空间方向性显著增加，而火焰对声波的敏感性逐渐降低，声波作用下的火焰形态变化示意图如图3和表1所示.

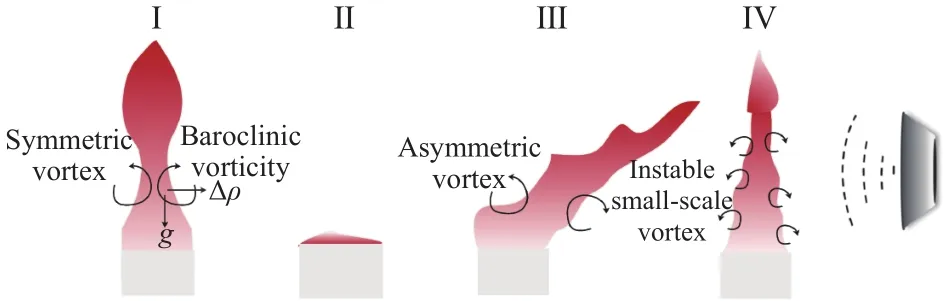
图3 油池火焰在声波作用下火焰形态变化示意图（I、II、III、和IV分别表示无声波作用、间歇截断、偏转和稳定燃烧的状态）Fig.3 Schematic diagram of flame shape change with acoustic force (I,II, III, and IV represent the nonacoustic, intermittent, deflective, and stable states, respectively)

表1 不同直径油池火焰在不同频率声波作用下的燃烧状态Table 1 State of pool flames with different diameters and different frequencies of acoustic force

2.2 火焰几何尺寸

由于原始火焰图像的数量较大，为了进一步定量分析火焰几何尺寸，利用图像二值化技术批量处理火焰图像.其原理为：将图像转化为像素点的二维矩阵，再设置一个或多个灰度阈值，比较图像中各像素的灰度值与阈值的大小关系，根据比较结果重新对矩阵赋值，从而将图像的对应像素分成两类或多类[21].本文选取40作为亮度阈值将图像的像素分为火焰部分（灰度值为1）和非火焰部分（灰度值为0），如图4(a)所示，确定竖直方向与水平方向上灰度值为1的边界点，根据像素点数量计算火焰尺寸，火焰面积定义火焰部分像素点数量之和，火焰宽度定义为边界点在水平方向上所间隔的最大的像素点数量，火焰高度定义为边界点在竖直方向上所间隔的最大的像素点数量.60 Hz频率声波作用下4 cm直径油池的火焰面积如图4(b)所示.由于声强迫作用下火焰往复振荡，为更好地反映火焰在一段时间内的整体特征，计算声波作用时间段内火焰尺寸的平均数值，图5为不同声频率下8 s内的平均火焰面积、平均火焰宽度和平均火焰高度及标准差.

图4 火焰图像二值化处理及火焰面积像素点数.(a)图像二值化处理；(b)火焰面积像素点数Fig.4 Binarization of flame image and number of flame area pixels: (a) binarization of flame image; (b) number of flame area pixels

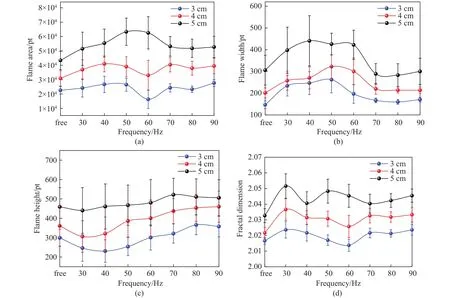
图5 不同直径油池火焰在不同声频率下的火焰面积、火焰宽度、火焰高度以及分形维数的平均数值.(a)火焰面积; (b)火焰宽度; (c)火焰高度;(d)分形维数Fig.5 Average flame area, flame width, flame height and fractal of pool flames with different diameters under acoustic wave of different frequencies: (a)flame area; (b) flame width; (c) flame height; (d) fractal dimension

由图5可以看出，3 cm和4 cm直径油池火焰具有相同的几何形态变化趋势：在间歇截断频率下，平均火焰面积小幅度增加，在进入偏转频率时火焰面积迅速下降，在进入稳定燃烧频率时保持稳定.5 cm直径油池的平均火焰面积在偏转频率下持续增加，进入稳定燃烧频率时面积下降并保持稳定.这是由于5 cm直径油池火焰具有更大火焰尺度，声波扰动引起的流场扰动卷吸预混的助燃作用大于热量损失带来的影响.平均火焰宽度和平均火焰高度变化趋势也印证了这一点，三种直径油池火焰的平均宽度在增加的情况下，5 cm直径油池的火焰高度相对稳定，而3 cm和4 cm直径油池火焰的火焰高度显著降低，表明前者火焰体积增加而后者则无.当频率增加至70 Hz以上时，三种直径油池的平均火焰宽度与自由燃烧时相近，但火焰高度和火焰面积都有所增加.由2.1的分析可知，随着声波频率的增加，火焰表面的涡旋数量增多尺度减小，掺混效率和燃烧效率提升，羽流的上升速度在表面涡旋的作用下增加，因此火焰高度也有了提升.

火焰在声波作用下加剧几何表面的皱褶程度，通过分形维数的计算能够分析火焰面的皱褶情况[22]，分形理论的数学表示为：

式中，F为n维空间下的有界集合，F有Nr个互不重合的子集，r为所有坐标方向上的尺度因子，DF为F的分形维数.本文中分形维数计算采用传统的数盒子法[23]，利用MATLAB计算三种直径的油池火焰在不同声频率下的平均分形维数，计算结果如图5（d）所示.

由图5（d）可知，火焰分形维数随油池直径的增大而增大，火焰羽流范围的增加引起火焰面拓展，出现更多皱褶空间.三种直径油池火焰均在30 Hz声强迫下的平均分形维数最大，由前文分析可知，由于水平方向的压力梯度变化引起涡量加强和涡旋运动显著影响火焰区域，火焰处于高度不稳定状态，火焰面弯曲皱褶，几何特征复杂；与5 cm直径油池不同的是，3 cm和4 cm直径油池火焰均在声强迫频率为60 Hz时分形维数最小，这是由于火焰面积的减小限制了表面皱褶的能力.

2.3 火焰信号频域特性

火焰的不稳定燃烧可通过火焰的热释放速率、火焰高度、火焰面积等参数的频域特性来反映[24].为分析火焰信号在不同状态的频域特性，对不同频率的火焰宽度、火焰面积及火焰高度的时域信号进行快速傅里叶变换（Fast fourier transform，FFT）分析.图6为三种直径油池火焰在30、50和70 Hz声波条件下的快速傅里叶变化结果.

图6 不同直径油池火焰在声波强迫下的频域信号(a、b和c前缀分别表示在30、50和70 Hz声波作用下；1、2和3后缀分别表示火焰面积、火焰宽度和火焰高度信号)Fig.6 Frequency signals of pool flames with different diameters under an acoustic force (a, b, and c prefixes denote acoustic wave at 30, 50, and 70 Hz,respectively; 1, 2, and 3 suffixes indicate the flame area, flame width, and flame height signal, respectively)

从幅值上看，火焰面积、宽度和高度数值的FFT结果中的幅值随油池直径的增加而增加；此外，输入的声波信号频率越低，在低于火焰振荡频率的频域内（0 ～ 10 Hz）峰值越集中，表明低频声波对火焰结构的破坏更为明显，导致火焰信号极不稳定；当输入的声信号为70 Hz时，由于火焰重新趋于稳定，频域分布趋于自由燃烧下的频域分布，但此时主频和次频的幅值降低，次频不显著，表明此时声波降低了正常的火焰脉动幅度.

从峰值频率上看，间歇截断状态和稳定燃烧状态下的声信号在火焰面积的频域分布中不易识别，而偏转状态下峰值较为明显，这是由于偏转状态下火焰结构更为完整，周期规律性更强.火焰高度无法识别出70 Hz的声信号，火焰宽度则不受限制，声信号在火焰宽度频域分布中始终突出.这是由于声波方向与火焰羽流方向垂直，声波扰动引起横向压力梯度相对于受控于重力和浮力作用引起的垂直压力梯度更大，火焰在横向方向的扰动更为显著；70 Hz声频率下火焰的频域分布除火焰自身的脉动频率外还存在噪点，表明火焰在稳定燃烧频率下依然存在小振幅脉动.

2.4 火焰理查德森数

针对横风作用下的油池火焰，Majeski等[25]和Shang 等[26]通过 Richardson（Ri）数，即火焰受到浮力与惯性力之比分析火焰不稳定性.

式中：Δρ为侧风密度与燃烧产物的密度差，kg·m-3；ρf为火焰密度，kg·m-3；L为油池特征尺寸，一般取油池直径，m；g为重力加速度，m·s-2；U为侧风风速，m·s-1.Ri数值越大，表示火焰处于越稳定的状态，反之火焰越不稳定.

刘鹏翔[27]通过推导和研究发现小尺度油池火焰在环境风作用下的Ri-1和火焰倾角的正切值存在一次函数关系：

式中，tanθ为火焰倾角的正切值，定义为水平位移与和火焰高度的比值；A和B为常数项.

与侧风类似，横向声波同样会引起火焰水平动量扰动和火焰倾角的特征性变化.此外，声波作用下的火焰不稳定性还对频率有明显依赖性.因此借助火焰倾角与Ri数的关系分析声波作用下的Ri数的形式，将式（3）的U带入当地空气振动速度，通过当地扰动声压的有效声压表示[21]：

式中，P为当地扰动有效声压，Pa；ρ为介质静态密度，kg·m-3，通过下式得到：

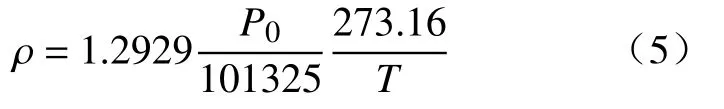
式中，P0为静态气压，Pa；T为介质温度，K.经由实验测得3、4和5 cm直径油池在自然状态下的火焰中心温度分别为384.2，453.6和564.7 ℃，取火焰中心温度与28 ℃空气温度的平均温度作为介质温度即火焰平均温度，进而得到介质密度和以及与外侧密度之差.

式（4）中火焰倾角正切值在本文采用平均火焰宽度的偏移与平均火焰高度之比表示.带入数值得到火焰倾角与声频率的关系如图7（a）所示.由此认为声波频率与火焰倾角的正切值存在近似反正切函数关系，在此基础上增加频率修正系数Z，使火焰倾角的正切值与Ria数的倒数满足一次函数关系，即：

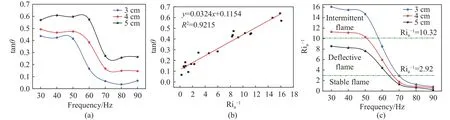
图7 声波频率、火焰倾角和Ria-1值之间的关系.(a)不同频率下的火焰倾角正切值; (b) Ria-1值与火焰倾角正切值的拟合关系; (c)火焰Ria-1值Fig.7 Relationship between acoustic frequency, flame angle, and Ria-1: (a) tangent value of flame inclination angle at different frequencies; (b) fitting relationship between Ria-1 and the tangent value of flame inclination angle; (c) flame Ria-1 value

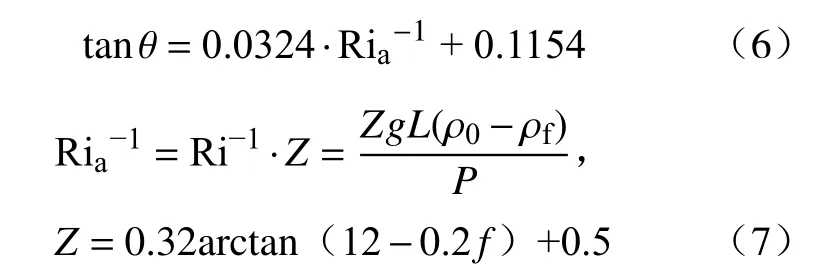
式中，Ria表示声波作用下的火焰Richardson数；Z为频率修正系数，根据实验结果拟合得到；ρ0为环境气体密度，kg·m-3；f为声频率，Hz.火焰倾角正切值与Ria数倒数拟合得到的一次函数关系如图7（b）.为进一步分析声频率对火焰不稳定性的影响，得到声频率与Ria数的关系如图7（c），为方便与无声波作用下的火焰Ri值进行对比（无声波作用时空气振动速度u≈0，Ri趋于无穷），Ria值均采用倒数的形式进行讨论.

由图7（c）可知，Ria-1值随着油池的直径增加而降低，对应了油池尺度对声波强迫的敏感性随着尺度的增加而降低；当外加声压大小相同时，随着声信号频率的增加，Ria-1值呈降低的趋势，对应了火焰不稳定性随声频率的增加逐渐减弱的演变关系.此外，三种直径油池火焰Ria-1值收敛于接近0的数值对应当声波频率超过一定数值时火焰近乎不再发生扰动，即与自然燃烧近乎无异（Ri=0）.因此，增加频率修正系数后的Ria数的结果与实验现象有较好的符合，在描述声波作用下的油池火焰稳定性方面具有一定可靠性.在此基础上可以发现，在50 ～70 Hz之间，Ria-1值随频率增加下降的速率最大，表明此时火焰对声波频率的响应尤为显著，当声波频率高于或低于该段频率时，对火焰的影响存在边际效应.此外，结合表1可以发现，间歇截断状态，偏转状态和稳定燃烧状态存在临界Ria-1值，分别为10.32和2.92.

3 结论

（1）随着声波频率的增加，三种直径油池火的燃烧不稳定性逐渐减弱，涡旋逐渐由影响火焰结构的内部区域转移至火焰表面的轮廓线，涡旋直径也逐渐变小；3 cm和4 cm直径油池火焰的间歇截断和偏转状态的临界频率分别频率为50 Hz和40 Hz，5 cm直径油池火焰由于热释放速率的增加，对声波扰动的敏感性降低，不存在间歇截断频率；三种油池火焰均在70 Hz时由偏转状态转变为稳定燃烧状态.

（2）3 cm直径和4 cm直径油池火焰在声波作用下有相似的几何形态变化趋势，当声波频率增加至70 Hz以上时，三种直径油池的平均火焰宽度与自由燃烧时相近，火焰高度和火焰面积都有所增加；分形维数分析表明火焰在间歇截断状态下和不稳定偏转状态下的皱褶程度最高.

（3）火焰信号的频域分析表明输入的声波信号频率越低，在低于火焰振荡频率的频域范围内峰值越集中；相较于间歇截断状态和稳定燃烧状态，声波频率在偏转状态下的频域信号中更明显；声频率在火焰宽度的频域分布中始终突出.

（4）火焰倾角正切值与声波频率近似存在反正切函数关系，通过火焰倾角与Ri数的关系得到声波作用下的火焰Ria数形式，Ria数值结果与实验现象具有较好的符合；对于同一水平声压大小下的声波，火焰存在对于频率的显著响应区间；间歇截断状态，偏转状态和稳定燃烧状态存在临界Ria-1值，分别为10.32和2.92.